Standardpotential

Das Standardpotential $\boldsymbol{E^{0}}$

Die Frage, die wir uns bei Redox-Reaktionen immer stellen, bezieht sich auf das Oxidations- und das Reduktionsmittel und welche der beteiligten Verbindung, welche dieser beiden Rollen einnimmt. Das Augenmerk dieses Skripts ist darauf gerichtet, die Eigenschaft von Redox-Paaren zu charakterisieren, die die Rolle des Oxidationsmittels bzw. des Reduktionsmittels bestimmt: Das Standardpotential. Nachdem wir diese Größe kennen gelernt haben, werden wir verschiedene Redox-Paare nach dieser Eigenschaft ordnen können und in diesem Zusammenhang die elektrochemische Spannungsreihe kennen lernen. Im letzten Kapitel gehen wir weg von den Standardbedingungen und somit vom Standardpotential hin zum allgemeineren Redoxpotential und insbesondere zu dessen Konzentrationsabhängigkeit. Letztere können wir dann mithilfe der Nernst-Gleichung beschreiben und auswerten.

Wir wollen dieses Skript mit einer relativ einfachen beispielhaften Redox-Reaktion beginnen, welche beispielsweise die Verbrennung von Magnesium sein könnte.Wir betrachten also die Oxidation von elementarem Magnesium durch Sauerstoff.

$2\,\text{Mg}_{(\text{s})}+\text{O}_{2\,(\text{g})}$ $\longrightarrow$ $2\,\text{MgO}_{(\text{s})}$

Der elementare Sauerstoff ist in dieser Reaktion für die Oxidation des Magnesiums zuständig, ist also das Oxidationsmittel und wird somit durch die Aufnahme von zwei Elektronen reduziert. Das elementare Magnesium reduziert den Sauerstoff durch die Abgabe von zwei Elektronen: Magnesium ist das Reduktionsmittel und wird oxidiert. In dieser Redox-Reaktion haben wir folgende Redoxpaare:

$\text{Mg}/\text{Mg}^{2+}$
$\text{O}_{2}/2\,\text{O}^{2-}$

Nun wollen wir diese Redox-Reaktion von einer etwas anderen Perspektive betrachten. In unserem Beispiel wussten wir aus irgendeinem Grund von Anfang an, dass Sauerstoff reduziert und Magnesium oxidiert werden würde. Aber warum? Die Frage, die wir eigentlich zu Beginn hätten klären müssen, könnte beispielsweise so lauten: Welches der beiden Edukte ist das Reduktionsmittel und welches das Oxidationsmittel? Welches Element ist also eher bestrebt, Elektronen abzugeben und welches ist bestrebt, Elektronen aufzunehmen? Um diese Frage zu klären, betrachten wir hier eine neue Größe: das Standardpotential $E^{0}$ .
Wir greifen auf die Oxidation von Magnesium zurück, die einer Halbreaktion der oben dargestellten Redox-Reaktion entspricht.

$\text{Mg}$ $\rightleftharpoons$ $\text{Mg}^{2+}+2\,\text{e}^{-}$

Bei dieser Reaktion werden Elektronen abgegeben und bei der Rückreaktion, also der Reduktion von elementarem Magnesium, werden Elektronen aufgenommen. Weiterhin können wir aus dieser Teilreaktion nicht ablesen, welche der beiden Richtungen bevorzugt ist: Wird $\text{Mg}$ „lieber“ oxidiert oder wird $\text{Mg}^{2+}$ „lieber“ reduziert? Da wir immer Redoxpaare betrachten, müssen wir das jeweilige Bestreben der beiden Partner zusammen betrachten und schauen, welcher der beiden letztendlich dominiert. Wir wollen versuchen uns diesen Umstand graphisch klar zu machen. Das soll nur eine Hilfestellung sein, damit du dir vorstellen kannst worum es hier geht:

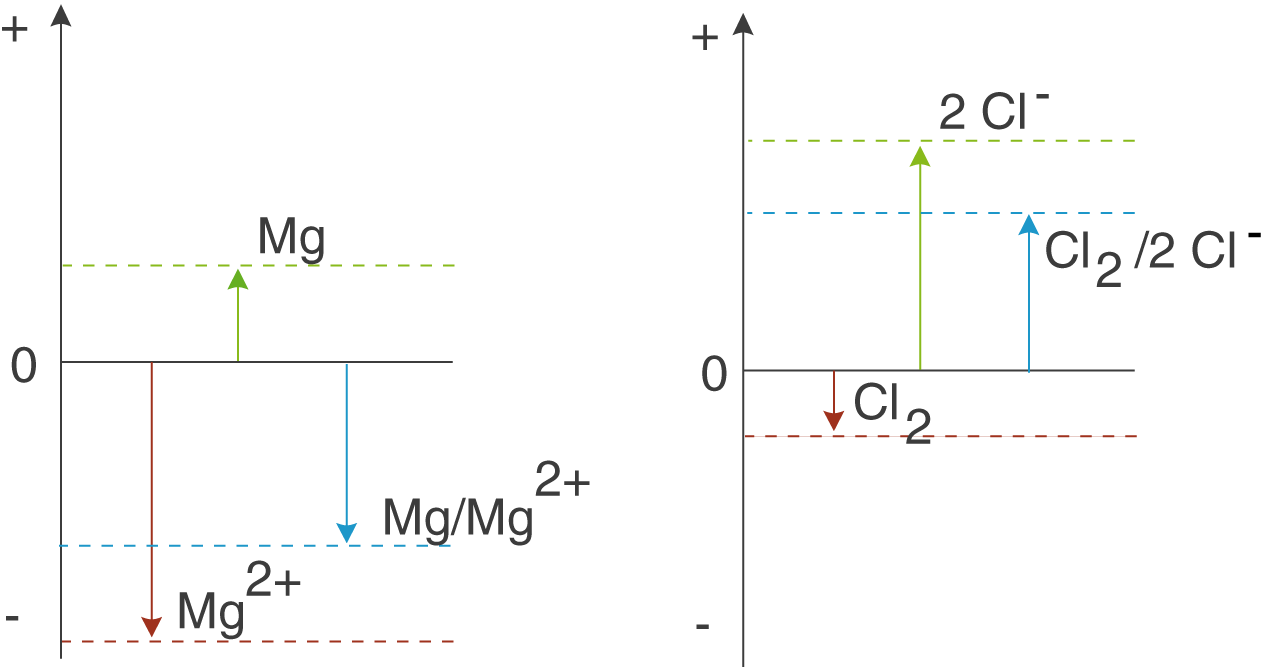
Diagramm mit elektrochemischen Potenzialen von Magnesium und Chlor.

Abb. 1: Unterschiedliche Potentiale von Magnesium und Chlor

Wir beginnen mit dem linken Schaubild. Die positive Richtung der Achse steht für das Bestreben, reduziert zu werden: Zu einem gewissen Grad besitzt $\text{Mg}^{2+}$ das Bestreben, $\text{Mg}$ reduziert zu werden. Die negative Richtung der Achse steht hingegen für das Bestreben, oxidiert zu werden, also Elektronen abzugeben. Um dieses Bestreben quantifizieren zu können, betrachten wir die Länge der Pfeile: Je länger ein Pfeil in eine bestimmte Richtung, desto höher ist das Bestreben dieses Stoffes in dieser Hinsicht. Für das Beispiel Magnesium erhalten wir damit Folgendes: Das Bestreben, dass $\text{Mg}^{2+}$ gebildet wird (roter Pfeil), also das elementares Magnesium oxidiert wird, ist größer, als das Bestreben, das $\text{Mg}^{2+}$ reduziert wird (grüner Pfeil). Kombinieren wir diese beiden Pfeile, dann erhalten wir den blauen Pfeil. Insgesamt dominiert also das Bestreben, dass elementares Magnesium oxidiert wird. Magnesium ist ein relativ starkes Reduktionsmittel.

Nun zum rechten Schaubild. Du kannst sehen, dass der rote Pfeil, der das Bestreben von $2\,\text{Cl}^{-}$ zu $\text{Cl}_{2}$ oxidiert zu werden veranschaulicht, hier wesentlich kürzer ist. Dahingegen ist der grüne Pfeil, welcher das Bestreben von $\text{Cl}_{2}$ , zu $2\,\text{Cl}^{-}$ reduziert zu werden, deutlich länger. In der Summe dominiert das Bestreben, dass elementares Chlor reduziert wird und somit zur Oxidation anderer Verbindungen beiträgt: Chlor ist ein relativ starkes Oxidationsmittel.

Wir haben das Bestreben von Redox-Paaren, als Oxidations- oder Reduktionsmittel zu wirken, durch die Verwendung von Pfeilen mit unterschiedlichen Längen quantifizieren können. Um das ganze nun praktischer zu gestalten, können wir auch eine Größe einführen, deren Zahlenwert quasi die Länge des blauen Pfeils darstellt: Das Standardpotential $E^{0}$ .

Das Standardpotential $E^{0}$ ist eine elektrochemische Messgröße, welche das Bestreben eines Redox-Paares, reduzierend oder oxidierend zu wirken, quantifiziert. Es ist für Standardbedingungen definiert und besitzt die Einheit Volt.

Die elektrochemische Spannungsreihe

Im letzten Kapitel haben wir das Standardpotential kennen gelernt. Wir wollen uns nun verschiedene Redox-Paare anschauen und eine gewisse Ordnung schaffen. Dazu betrachten wir drei verschiedene Redox-Paare.

1. $\text{Mg}/\text{Mg}^{2+}$

$\text{Mg}$ $\rightleftharpoons$ $\text{Mg}^{2+}+2\,\text{e}^{-}$

2. $\text{Cl}_{2}/2\,\text{Cl}^{-}$

$\text{Cl}_{2}+2\,\text{e}^{-}$ $\rightleftharpoons$ $2\,\text{Cl}^{-}$

3. $\text{H}_{2}/2\,\text{H}^{+}$

$\text{H}_{2}$ $\rightleftharpoons$ $2\,\text{H}^{+}+2\,\text{e}^{-}$

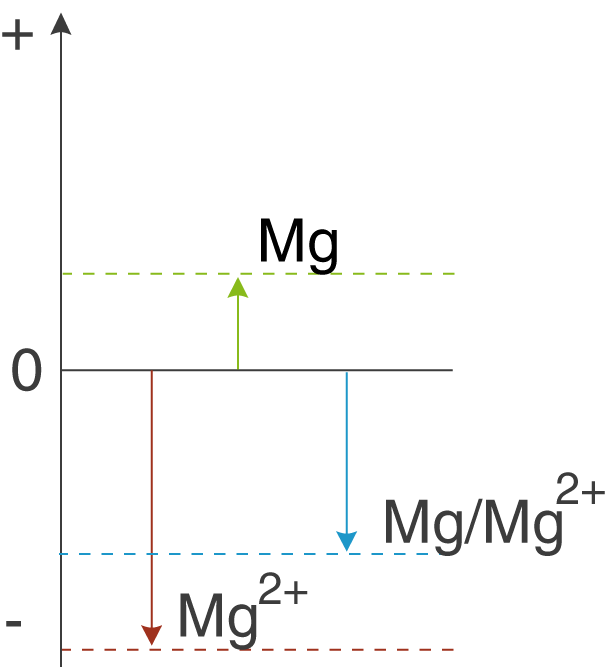
Wir wollen uns zunächst auf die beiden ersten Teilreaktionen konzentrieren. Für die Oxidation von Magnesium wurde experimentell folgendes Standardpotential ermittelt: $E^{0}(\text{Mg}/\text{Mg}^{2+})=-2,263\,\text{V}$ . Das Redox-Paar $\text{Mg}/\text{Mg}^{2+}$ besitzt demzufolge ein Standardpotential von $-2,263\,\text{V}$ . Wir wollen diesen Wert nun noch einmal auf die Graphik aus dem letzten Kapitel beziehen:

Du siehst, dass der blaue Pfeil in die negative Richtung der Achse zeigt. Wir hatten weiter oben gesagt, dass dies darauf zurückzuführen ist, dass das Bestreben von Magnesium, oxidiert zu werden größer ist, als das von $\text{Mg}^{2+}$ , reduziert zu werden. Wir können dieses Bestreben nun durch ein Standardpotential von $E^{0}(\text{Mg}/\text{Mg}^{2+})=-2,263\,\text{V}$ quantifizieren und sind nicht länger auf die relativ ungenau Angabe der Pfeillänge angewiesen.

Diagramm zur Darstellung von Redox-Potenzialen mit Magnesium und Magnesiumionen.

Abb. 2: Unterschiedliche Potentiale des Magnesiums

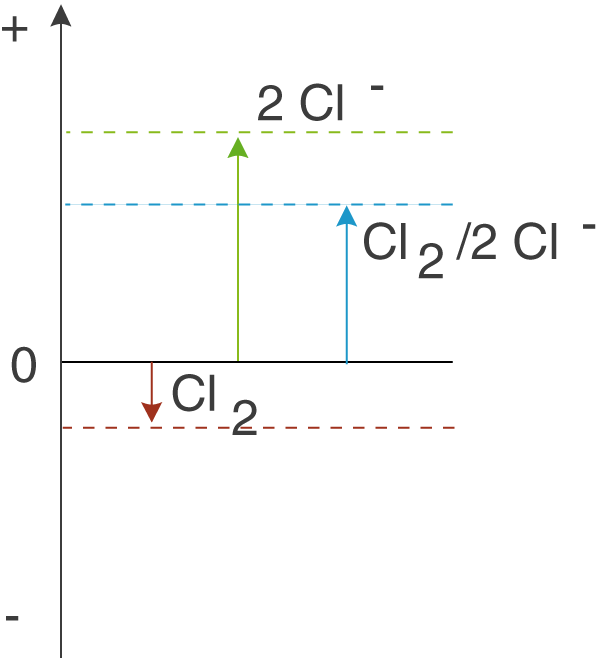
Für die Reduktion von elementarem Chlor finden wir ein Standardpotential von $E^{0}(\text{Cl}_{2}/2\,\text{Cl}^{-})=+1,36\,\text{V}$ . Im Vergleich zur zweiten, oben aufgeführten Graphik passt das ebenfalls wieder:

Der blaue Pfeil zeigte in diesem Fall in die positive Achsenrichtung: Das Bestreben von Chlorid besteht darin, reduziert zu werden und diese Eigenschaft dominiert somit das Redox-Paar.

Diagramm mit verschiedenen Linien und Pfeilen, die chemische Gleichgewichte darstellen.

Abb. 3: Unterschiedliche Potentiale des Chlors

Nun zum letzten Beispiel. Dieses ist etwas Besonderes. Um das zu verstehen, greifen wir auch hier auf die betrachteten Schaubilder zurück. Wie du sehen kannst, haben wir die Pfeile ohne Begründung relativ zu einem bestimmten Nullpunkt gesetzt. Übertragen auf die beiden Redox-Paare, so bedeutet dies, dass wir bisher keine Erklärung dafür habe, warum das eine Standardpotential negativ ist und das andere positiv: Uns fehlt ein Nullpunkt.
Dieser Nullpunkt der Standardpotentiale wird konventionell auf die Redox-Reaktion von elementarem Wasserstoff gelegt. Es gilt:

$\boldsymbol{E^{0}(\text{H}_{2}/2\,\text{H}^{+})=0,00\,\text{V}}$

Damit haben wir einen Bezugspunkt festgelegt, auf den wir die anderen Redoxpotentiale beziehen können. Nun kommen wir auf den Punkt zurück, den wir am Anfang angedacht hatten: Ordnung schaffen im Bezug auf die Redoxpaare. Wenn wir hierbei noch andere Redoxpaare miteinbeziehen, dann erhalten wir die elektrochemische Spannungsreihe, die wir uns nun etwas genauer anschauen wollen.

Wir wollen uns nun einige Besonderheiten der elektrochemischen Spannungsreihe anschauen und lernen, wie sie zu lesen ist. Wir sehen in der linken Spalte jeweils die reduzierte Form eines Redoxpaares und in der mittleren die oxidierte Form. Die vierte Spalte gibt uns Informationen über die Anzahl der übertragenen Elektronen und in der fünften Spalte stehen die Standardpotentiale der jeweiligen Teilreaktionen in Volt.

(1) Tendenzen

Die Stärke des Reduktionsmittels nimmt mit abnehmendem Standardpotential zu. Das heißt, dass Lithium ein stärkeres Reduktionsmittel ist als Eisen. Die Stärke des Oxidationsmittels nimmt mit steigendem Standardpotential zu. $\text{Cu}^{2+}$ ist ein schwächeres Oxidationsmittel als beispielsweise $\text{Au}^{3+}$ .
Beispielhaft können wir eine Reaktion betrachten, die elementares Lithium und Ag(I)-Kationen enthält. Da Lithium das stärkere Reduktionsmittel ist und $\text{Ag}^{+}$ nicht weiter oxidiert werden kann, fungiert letzteres als Oxidationsmittel: Diese Reaktion würde also ablaufen. Andersherum wäre das nicht möglich. $\text{Li}^{+}$ -Kationen sind mit ihrem Zustand „sehr zufrieden“, das heißt, dass sie nur sehr ungern reduziert werden. Elementares Silber wäre nicht in der Lage $\text{Li}^{+}$ -Kationen zu reduzieren.

(2) Lesen der elektrochemischen Spannungsreihe

Betrachte eine beliebige gegeben Reaktion und suche die Teilreaktionen in der elektrochemischen Spannungsreihe.

Steht die reduzierte Form der beteiligten Reaktanden links über der oxidierten Form, dann ist die Reaktion möglich.
Steht die oxidierte Form der beteiligten Reaktanden rechts über der reduzierten Form, dann ist die Reaktion nicht möglich.

Beispielsweise könnte eine Redox-Reaktion zwischen Li und $\text{Fe}^{2+}$ stattfinden, wohingegen eine Redox-Reaktion zwischen $\text{Li}^{+}$ und Fe nicht stattfinden würde.

Wichtig:
Zwei Aspekte sind zu beachten: Wenn du von einem Oxidationsmittel sprichst, dann muss die entsprechende Form des Elements auch reduzierbar sein. Das heißt, dass du im Allgemeinen immer den richtigen Partner des Redox-Paares betrachten musst. Li kann beispielsweise ein starkes Reduktionsmittel sein; $\text{Li}^{+}$ hingegen ist kein starkes Reduktionsmittel. Die Oxidation von Li ist ja schon stark bevorzugt und Li kann unter normalen Umständen nicht weiter als zu $\text{Li}^{+}$ oxidiert werden. Beachte, dass du Redox-Paare immer relativ betrachtest, das heißt, dass du keine absolute Aussage darüber treffen kannst, ob ein Redox-Paar oxidierend oder reduzierend wirkt. Zum einen musst du die vorliegende Spezies beachten, das heißt, welche Oxidationszahl weist der vorliegende Stoff auf und zum anderen kann es natürlich sein, dass ein anderes Element vorliegt, welches eine der beiden Eigenschaften dominiert. Eisen ist nach der Spannungsreihe bspw. ein relativ starkes Reduktionsmittel, aber nur wenn wir Kupfer- oder Silber-Kationen in der Lösung haben. Ein Lithiumkation könnte nicht durch Eisen reduziert werden.

(3) pH-Wert und Redox-Reaktionen

Das Standardpotential ist für Standardbedingungen definiert. Diese beinhalten jedoch nicht die Festlegung eines bestimmten pH-Werts! Werden die Standardbedingungen nicht eingehalten, dann entspricht dieses Potential dem Redoxpotential. Im Falle von Standardbedingungen entspricht das Redoxpotential also gerade dem Standardpotential.
Dieses Redoxpotential ist neben der Temperatur und dem pH-Wert auch von dem Konzentrationsverhältnis des jeweiligen Redox-Paares abhängig. Wir werden diese Tatsache im nächsten Kapitel etwas näher betrachten, wenn wir einen Blick auf die Nernst-Gleichung werfen. Des Weiteren spielt dieser Aspekt insbesondere im Skript Elektrochemische Stromquellen und Speicherung von Energie eine wichtige Rolle, wenn wir die Potentialdifferenz des Bleiakkus berechnen.

(4) Edle und Unedle Metalle

Je edler ein Metall, desto positiver ist sein Standardpotential. Gold ist beispielsweise sehr viel edler als Eisen, gleichzeitig aber auch immer noch edler als Silber. Andererseits können wir aber auch sagen, dass Eisen edler ist als Lithium. In diesem Fall wäre das Eisen relativ gesehen edler. Du musst also auch hier immer zwei Redox-Paare betrachten, um eine solche Aussage treffen zu können. Gold ist zwar ein sehr edles Metall, trotzdem kannst du dir nicht ohne weiteres sicher sein, ob es nicht doch noch ein Metall gibt, was eventuell noch ein Stück edler ist. Absolute Aussagen sind hier also ebenfalls schwierig.

Die Nernst-Gleichung

Anmerkung: Die Nernst-Gleichung spielt in der Schule nur eine sehr untergeordnete Rolle. Wir wollen an dieser Stelle aber einen Blick darauf werfen und die Konzentrationsabhängigkeit des Redoxpotentials betrachten.

Die Nernst-Gleichung geht auf den deutschen Physiker und Chemiker sowie Nobelpreisträger von 1920 Walther Nernst zurück. Sie beschreibt unter anderem die Konzentrationsabhängigkeit des Redoxpotentials. Die Nernst-Gleichung lautet:

$E$ = $E^{0}+\dfrac{R\cdot T}{z\cdot F}\cdot\log\left(\dfrac{c(\text{Ox.})}{c(\text{Red})}\right)$

$E^{0}$ kennen wir bereits, das ist das Standardpotential des betrachteten Redox-Paares. $R$ ist die allgemeine Gaskonstante, $T$ ist die Temperatur, $z$ die Anzahl der übertragenen Elektronen und $F$ die Faraday-Konstante. $c(\text{Ox.})$ ist die Konzentration der oxidierten Form und $c(\text{Red})$ die Konzentration der reduzierten Form des Redox-Paares.
Wir wollen uns die Anwendung dieser Gleichung anhand des Redox-Paares von Magnesium $\text{Mg}/\text{Mg}^{2+}$ anschauen. Hier ist $c(\text{Ox.})=c(\text{Mg}^{2+})$ und $c(\text{Red})=c(\text{Mg})$ . Insgesamt werden bei dieser Reaktion zwei Elektronen übertragen. Damit ist $z=2$ .

(1) $c(\text{Mg}^{2+})=c(\text{Mg})$

Für dieses Beispiel lautet die Nernst-Gleichung folgendermaßen:

$$ E(\text{Mg}/\text{Mg}^{2+})= $$ $$ ... $$

Vollständige Formel
anzeigen

Da die Konzentrationen der beiden beteilgten Stoffe gleich ist, können wir den Bruch, der das Argument des „Zehnerlogartihmus“ bildet, kürzen.

$E(\text{Mg}/\text{Mg}^{2+})$ = $E^{0}(\text{Mg}/\text{Mg}^{2+})+\dfrac{R\cdot T}{2\cdot F}\cdot\log(1)$ $\hspace{.3cm}\text{mit}\hspace{.3cm}$ $\log(1)=0$

Der Faktor vor dem Logarithmus ist konstant und der Logarithmus von eins gleich null. Damit fällt der zweite Term weg und wir erhalten:

$E(\text{Mg}/\text{Mg}^{2+})$ = $E^{0}(\text{Mg}/\text{Mg}^{2+})$

Das Redoxpotential entspricht also genau dann dem Standardpotential, wenn die Konzentrationen der Partner des Redox-Paares gleich sind.

(2) $c(\text{Mg}^{2+})=10\cdot c(\text{Mg})$

Was passiert, wenn wir bspw. die Konzentration von $\text{Mg}^{2+}$ zehnmal größer machen, wie die Konzentration von $\text{Mg}$ ?

$$ E(\text{Mg}/\text{Mg}^{2+}) = $$ $$ ... $$

Vollständige Formel
anzeigen

Wir setzen die Bedingung von oben ein und erhalten:

$$ E(\text{Mg}/\text{Mg}^{2+}) = 1 $$ $$ ... $$

Vollständige Formel
anzeigen

Damit ändert sich unser Redoxpotential folgendermaßen:

$E(\text{Mg}/\text{Mg}^{2+})$ = $E^{0}(\text{Mg}/\text{Mg}^{2+})+\dfrac{R\cdot T}{2\cdot F}$

Da wir die Temperatur auch als konstant annehmen, erhöht sich das Redoxpotential also um den Term $\dfrac{R\cdot T}{2\cdot F}$ . Wenn wir alle drei Konstanten zusammenrechnen, können wir diesen auch als $\dfrac{0,059\,\text{V}}{2}$ schreiben. Für eine konkrete Temperatur von $T=25^{\circ}\,\text{C}=289\,\text{K}$ bedeutet das dann:

$$ E(\text{Mg}/\text{Mg}^{2+})= -2,33\,\text{V} $$ $$ ... $$

Vollständige Formel
anzeigen

Wir sehen, dass das Bestreben, als Reduktionsmittel zu wirken, sinkt. Das können wir uns so erklären: Wir betrachten hier zehnmal mehr $\text{Mg}^{2+}$ -Kationen, als elementares Magnesium. Diese sind nicht bestrebt, als Reduktionsmittel zu wirken, denn sie können nicht weiter oxidiert werden. Das bedeutet, dass deren Einfluss dadurch größer wird, dass sie in einer sehr viel höheren Anzahl vorhanden sind.

(3) $10\cdot c(\text{Mg}^{2+})=c(\text{Mg})$

Nun schauen wir uns den umgekehrten Fall an. Analog könnten wir behaupten, dass der oben erkannte Effekt nun in die andere Richtung zu sehen sein müsste. Das Redoxpotential müsste sich für eine erhöhte Menge an elementarem Magnesium gegenüber dem Standardpotential verringern. Wir wollen das überprüfen:

$$ E(\text{Mg}/\text{Mg}^{2+}) = -1 $$ $$ ... $$

Vollständige Formel
anzeigen

Da der Faktor $\dfrac{R\cdot T}{2\cdot F}$ auch weiterhin konstant ist, erhalten wir für unser Beispiel:

$$ E(\text{Mg}/\text{Mg}^{2+}) = $$ $$ ... $$

Vollständige Formel
anzeigen

Wenn wir nun das Redoxpotential berechnen, kommen wir auf:

$$ E(\text{Mg}/\text{Mg}^{2+}) = -2,39\,\text{V} $$ $$ ... $$

Vollständige Formel
anzeigen

Dieses Ergebnis bestätigt unsere anfängliche Vermutung: Das Redoxpotential wird geringer, das heißt, dass die Wirkung als Reduktionsmittel zunimmt. Es ist mehr elementares Magnesium vorhanden, welches hier oxidiert werden kann und somit eine reduzierende Wirkung aufweist.

Bildnachweise [nach oben]

[1]

[2]

[3]