In diesem Skript werden wir lernen, das theoretische Wissen, das du im Bezug auf die Elektrochemie kennen gelernt hast, anzuwenden. Wir werden uns hier damit beschäftigen, wie Redoxreaktionen verwendet werden können, um beispielsweise eine Lampe zum Leuchten zu bringen. Hier wird folglich chemische in elektrische Energie umgewandelt.
Das Galvanische Element ist ein zentrales Element der Elektrochemie, welches eine spezifische Vorrichtung zur spontanen Umwandlung von chemischer in elektrische Energie darstellt. In diesem Skript wird es insbesondere wichtig werden, die Funktionsweise des Galvanischen Elements verstehen zu lernen, um an anderer Stelle den Begriff der Elektrolyse vom Galvanischen Element klar abgrenzen zu können.

Der Begriff des Galvanischen Elements geht auf den italienischen Arzt Luigi Galvani (18. Jahrhundert) zurück, welcher eher unwissentlich zu dessen Entwicklung beitrug. Galvani experimentierte mit Froschschenkeln und entdeckte dabei die Kontraktion von Muskeln. Diese Kontraktion trat genau dann auf, wenn zwei miteinander verbundene Kupfer- und Eisenstäbe mit den Muskeln in Berührung kamen. Ohne es zu wissen, hatte Galvani so einen Stromkreis geschaffen, welcher aus zwei Metallen und einer Salzlösung im Froschschenkel, dem Elektrolyten, bestand. Immer dann wenn der Stromkreis geschlossen wurde, floss ein elektrischer Strom durch die Froschschenkel, welcher die Muskelkontratkion zur Folge hatte. Die Vorrichtung, die bei diesem Experiment verwendet wurde, entspricht genau dem Aufbau des Galvanischen Elements.

Aufbau

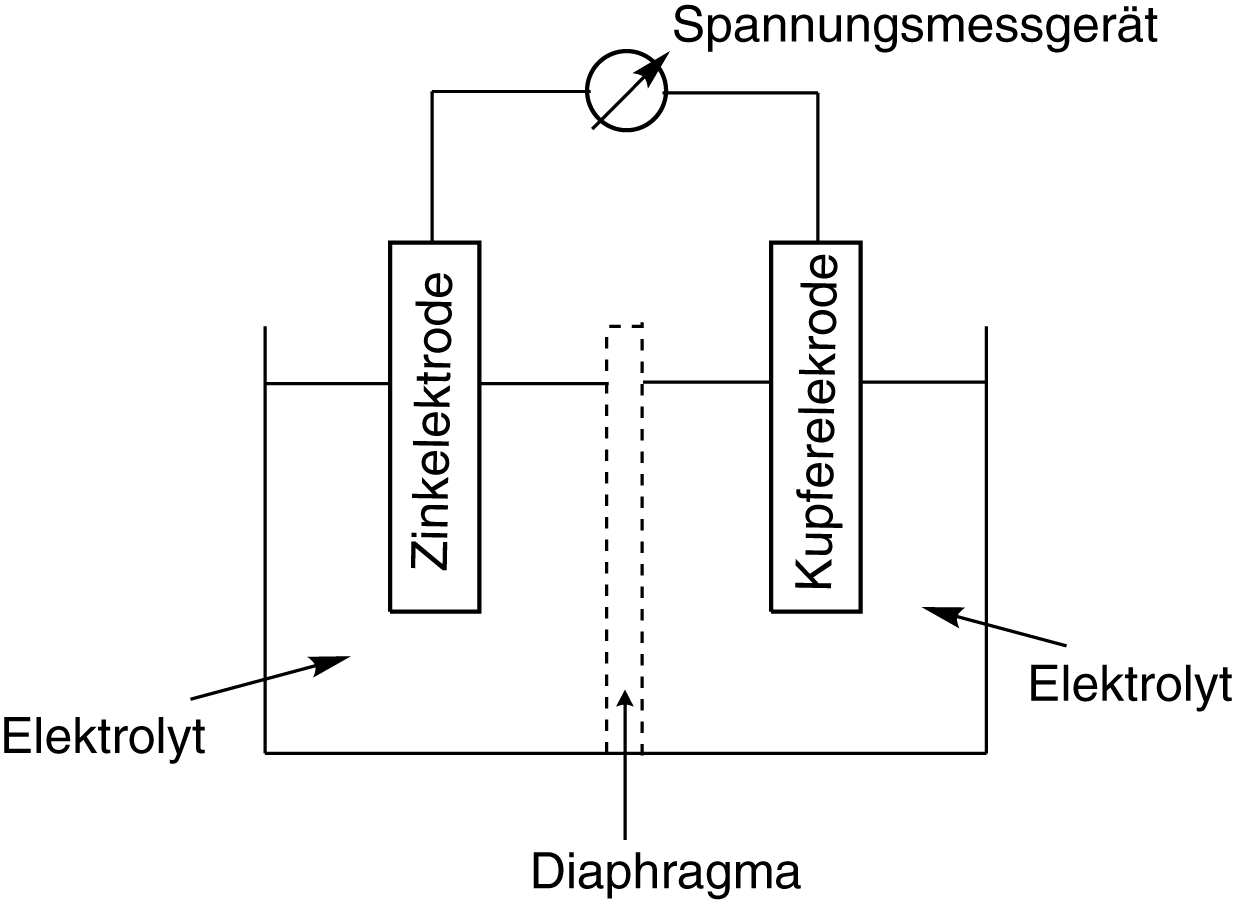
Der Aufbau eines Galvanischen Elements ist charakteristisch und weist einige Merkmale auf, die wir uns genau anschauen werden, auch wenn sie anfangs scheinbar trivial erscheinen. Unten siehst du ein spezielles Galvanisches Element, welches in diesem Aufbau die Bezeichnung des Daniell-Elements besitzt.

Anmerkung: Das Daniell-Element ist ein spezielles Galvanisches Element, welches die Elemente Zink (Zn) und Kupfer (Cu) kombiniert. Der Begriff des Galvanischen Elements umfasst also auch das Daniell-Element. Nicht dass du denkst, das Daniell-Element wäre eine Sache und ein Galvanisches Element eine andere: Ein Daniell-Element ist ein Galvanisches Element, wenn auch ein spezielles.

Ein Galvanisches Element besteht aus folgenden Komponenten:

• zwei Halbzellen,
• zwei räumlich getrennten Elektroden; pro Halbzelle eine,
• zwei Elektrolytlösungen,
• ein Diaphragma, das heißt eine permeable Membran, die ein Ionenaustausch zwischen den Halbzellen erlaubt,
• eine Kabel, welches beide Elektroden verbindet
• ein Spannungsmessgerät oder eine Lampe.

Ein sehr wichtiger Aspekt ist die räumliche Trennung der Elektroden. Wir gehen nun dazu über, diese sehr allgemeine Beschreibung elektrochemisch auszuwerten und zu konkretisieren, sodass wir letztlich die Funktion Galvanischer Elemente lernen und verstehen können.

Elektrochemische Betrachtung

Wir konkretisieren unsere Betrachtung jetzt und gehen auf alle Bestandteile des Daniell-Elements ein.

Hier hat sich im Vergleich zu oben eine ganze Menge geändert:

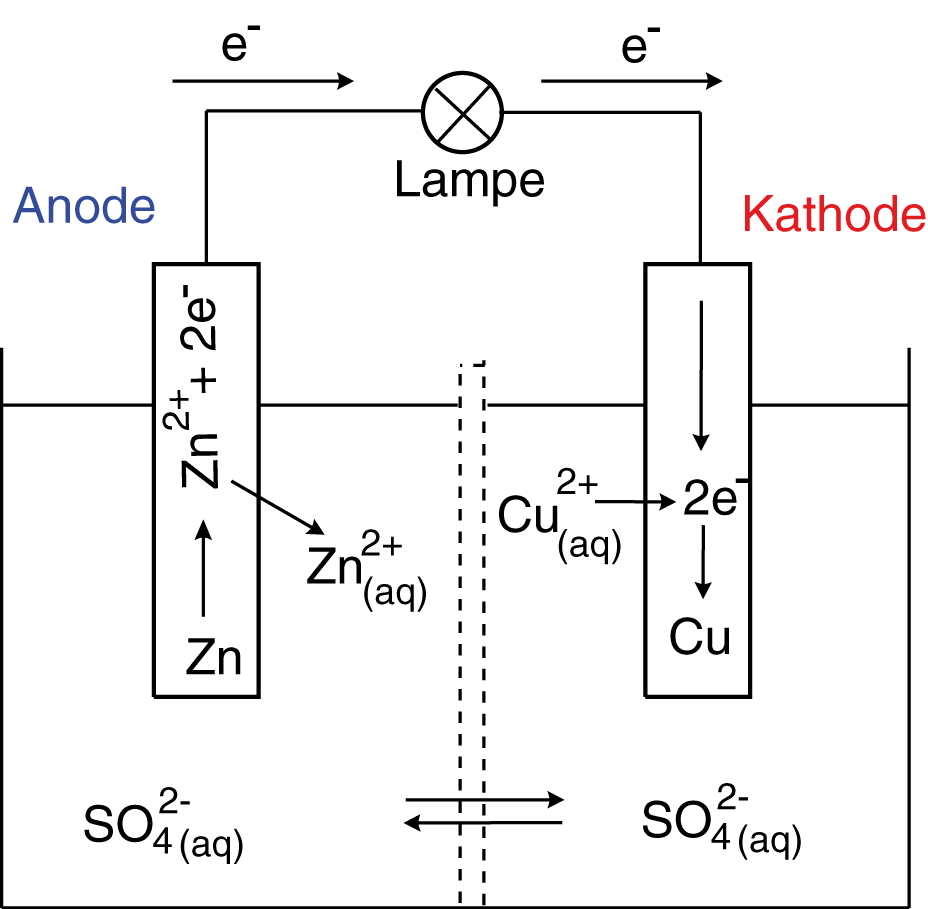
Halbzellen

Die Halbzellen des Daniell-Elements bestehen aus den Redox-Paaren und . Elementares Kupfer und Zink liegen in Form der Elektroden vor. Diese bestehen aus diesen Materialien. Die entsprechenden Kationen liegen in Form eines entsprechenden gelösten Salzes in wässriger Lösung vor: das Elektrolyt. Wichtig ist hierbei, dass wir Sulfat-Anionen () als Gegenionen in Lösung haben, damit ein Ladungsausgleich gegeben ist. Die Lösungen beider Halbzellen haben hier die gleiche Konzentration von .

Die Bezeichnung || steht für dieses Galvanische Element. Von links nach rechts haben wir die Zinkelektrode, das gelöste Zinksulfat, das gelöste Kupfersulfat und die Kupferelektrode. Die Striche „“ stehen für Phasengrenzen, bzw. „“ für das Diaphragma. Eine Phasengrenze bezeichnet eine Fläche, an der sich entweder der Aggregatszustand oder die Zusammensetzung ändert. Beispielsweise haben wir zwischen der festen Kupferelektrode (der Festphase) und dem wässrigen Elektrolyten (der Flüssigphase) eine solche Phasengrenze. Ein anderes Beispiel, welches nicht im Bezug zum Galvanischen Element steht, ist Öl, welches auf Wasser schwimmt. Dadurch, dass es nicht zur Lösung kommt, gibt es einen Bereich, an dem ein Wechsel zwischen Öl und Wasser stattfindet - die Phasengrenze.

Redox-Chemie des Daniell-Elements

Wir gehen nun dazu über die Prozesse der beiden Halbzellen bei Standardbedingungen zu betrachten. Wie wir bereits wissen, haben wir eine Halbzelle mit dem Redox-Paar und eine mit dem Redox-Paar . Wir können uns also die entsprechenden Standardpotentiale aus einem Tabellenwerk zusammensuchen:

• 
• 

Hier kannst du sehen, dass Kupfer das edlere Metall ist, also bestrebt ist, reduziert zu werden. Zink ist dahingegen das unedlere Metall und bestrebt, oxidiert zu werden. Für Einzelheiten vgl. das Skript Das Standardpotential und die elektrochemische Spannungsreihe. Damit laufen folgende Teilreaktionen in den Halbzellen ab:

Oxidation Reduktion

Die beiden Elektroden erhalten in diesem Zusammenhang neue Bezeichnungen: Anode und Kathode.

Zink ist in diesem Fall das Reduktionsmittel und wird oxidiert. Kupfer ist das Oxidationsmittel und wird reduziert.

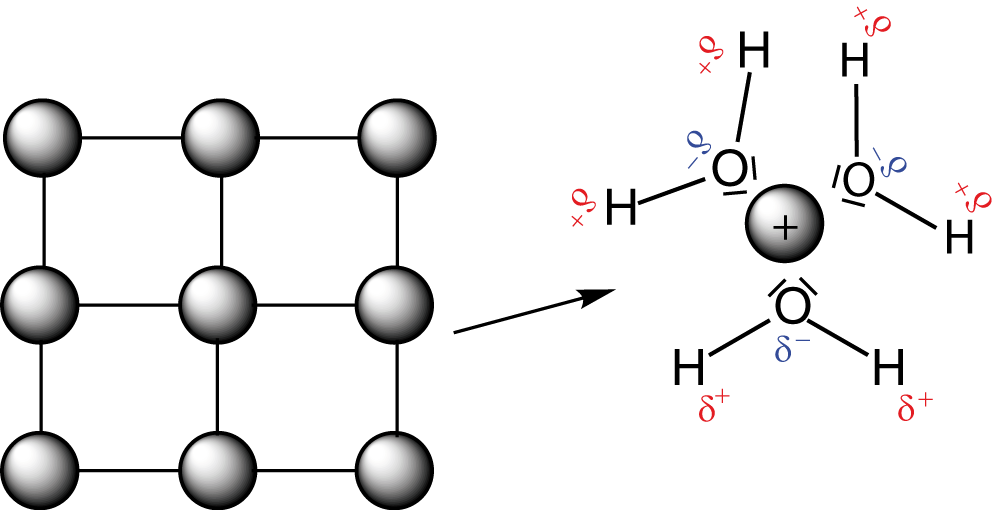
Wir kommen nun zur Erklärung, wie ein galvanisches Element funktioniert. Zunächst betrachten wir den Fall, dass beide Elektroden unverbunden sind. Die Größe, die nun ins Spiel kommt, nennt sich Lösungstension. Die Lösungstension beschreibt das Bestreben eines Metalls, in wässriger Lösung Ionen auszubilden. Wenn wir bspw. ein Stück Zink nehmen und es in Wasser legen, dann werden sich einige Zink-Kationen bilden und in Lösung gehen, während sich das Zinkstückchen durch die überschüssigen Elektronen leicht negativ aufladen wird. Die Lösungstension hängt dabei von zwei Parametern ab: Der Ionenkonzentration der Lösung und dem Energiegewinn, der bei dem Lösungsvorgang möglich wird.

Auf der linken Seite sehen wir hier einen zweidimensionalen Ausschnitt eines Kristallgitters, in dem die Atome eines Metalls regelmäßig angeordnet sind. Legen wir dieses Metall nun in Wasser, dann werden einzelne Kationen in Lösung gehen und dort von Wassermolekülen hydratisiert. Rechts sehen wir, dass das positiv geladene Kation beispielhaft von drei Wassermolekülen umgeben ist. Während dieses Hydratisierungsprozesses wird Hydratisierungsenergie frei. Diese Energie wird gegenüber dem gebundenen Zustand des Kations gewonnen. Da die Atome eine Zustand minimaler Energie anstreben, wird die Lösungstension durch die Energiedifferenz zwischen der Gitterenergie des Feststoffes und der Hydratisierungsenergie bestimmt: Je größer der Energiegewinn während des Lösungsprozesses, desto mehr Kationen gehen in Lösung und desto stärker ist die Lösungstension. Gehen Kationen von der Elektrode in Lösung, beobachten wir eine weitere Besonderheit: Die Ausbildung der Elektrochemischen Doppelschicht. Um diese zu erklären, zoomen wir an die Phasengrenze zwischen Elektrode und Elektrolyt. Dort erhalten wir theoretisch ungefähr folgendes Bild:

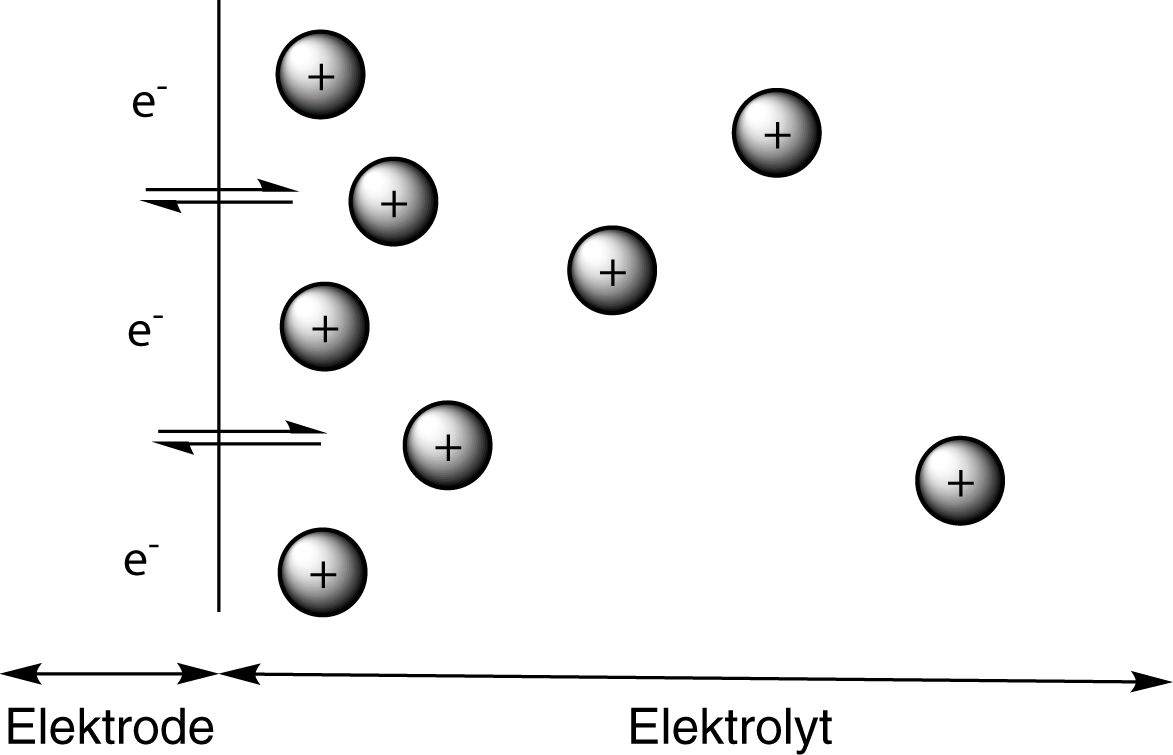
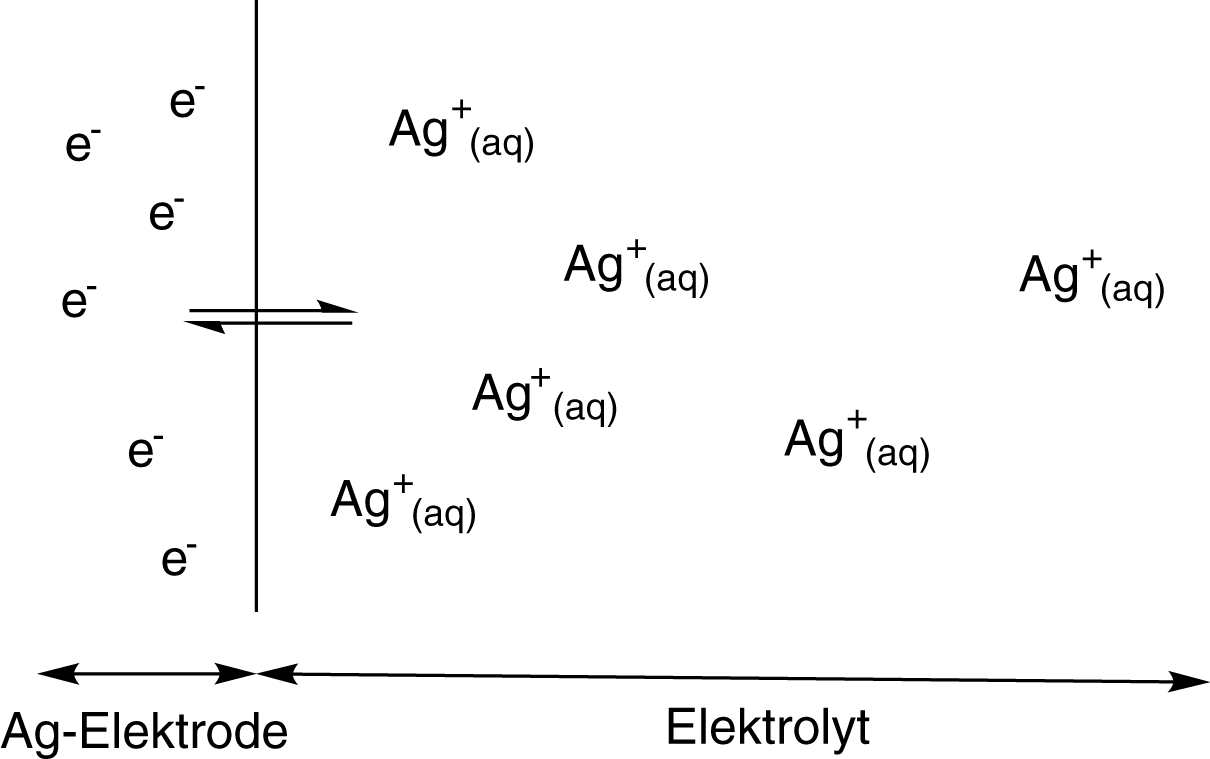
Die Phasengrenze zwischen Elektrode und Elektrolyt wird durch die schwarze Linie symbolisiert. Durch die Lösungstension werden Kationen (graue Kugeln mit einem Plus) in Lösung gehen, während die Elektronen auf der Elektrode verbleiben. Gleichzeitig werden die entsprechenden Kationen aber auch an der Phasengrenze durch eine Elektronenaufnahme wieder reduziert werden: Es stellt sich ein chemisches Gleichgewicht zwischen gelösten Kationen und Elektrodenmaterial ein. Wichtig ist hierbei, dass die Konzentration der Kationen mit der Entfernung zur Elektrode abnimmt. Das geschieht jedoch nicht abprubt, sondern relativ kontinuierlich oder auch diffus. Diese Tatsache verleiht der elektrochemischen Doppelschicht auch die Bezeichung diffuse Doppelschicht.

Wenn nun die Lösungstension eines Elektrodenmaterials größer ist als die des anderen, dann stellt sich aufgrund unterschiedlicher Mengen an Elektronen auf den beiden Elektroden eine Potentialdifferenz zwischen den beiden ein. Diese Potentialdifferenz wird Leerlaufspannung des Galvanischen Elements genannt und kann mit einem Voltmeter gemessen werden. Wichtig ist, dass unsere Redox-Reaktion bisher noch nicht ablaufen konnte, da ein Elektronentransfer von der einen zur anderen Elektrode nicht möglich war. Wir wollen uns den Begriff der Potentialdifferenz anhand eines Schaubildes klar machen. Dazu betrachten wir kleine graue Kugeln in Analogie zu den Elektronen:

Auf der linken Seite haben wir einen großen Berg grauer Kugeln, der für den Elektronenüberschuss an der Anode steht und ein großes Potential darstellt. Auf der rechten Seite haben wir hingegen einen erheblichen Mangel, sinnbildlich für die Kathode, also ein relativ geringes Potential. Das System ist bestrebt, diesen Unterschied bzw. diese Potentialdifferenz auszugleichen: Die Bälle vom linken Berg streben nach rechts, wenn sie die Möglichkeit bekommen, damit ein Ausgleich hergestellt wird. Wir wollen das Analogon hierzu nun in der Weise betrachten, dass wir beide Elektroden mit einem Kabel verbinden und eine kleine Lampe dazwischenschalten. Bei der Oxidation von Zink gehen zweiwertige Zink-Kationen in Lösung, während die Elektronen auf der Elektrode verbleiben. Die Zinkelektrode, hier die Anode, löst sich also langsam auf. Gleichzeitig wird auf der Seite der Kupferelektrode, der Kathode, der umgekehrte Prozess stattfinden: Zweiwertige Kupferkationen wandern aus der Lösung zur Kathode und werden dort reduziert. Diese Halbzelle wird auch Akkzeptorhalbzelle genannt. Die Reduktion ist aber nur mithilfe von Elektronen möglich, die von der Anode zur Verfügung gestellt werden, deshalb wird die Halbzelle der Anode dementsprechend Donatorhalbzelle genannt. Wir erhalten also folgende Situation: Durch die Oxidation von Zink und den Elektronenfluss zur Kathode wird die Reduktion von Kupferkationen möglich. Das bedeutet konkret, dass die Donatorhalbzelle im Bezug auf zweiwertige Kationen angereichert wird, während die Akkzeptorhalbzelle an zweiwertigen Kupfer-Kationen verarmt und die Elektrode wächst. Damit der Ladungsausgleich der beiden Halbzellen gegeben ist, können die Sulfat-Anionen in der Lösung durch das Diaphragma in die Donatorhalbzelle hindurchwandern und den Stromkreis so schließen. Den elektrischen Strom, der fließt, können wir nutzen, um die kleine Lampe zum Leuchten zu bringen.

Anmerkung: Du wirst oft den Hinweis finden, dass die Anode im Falle des Galvanischen Elements den Minuspol und die Kathode den Pluspol darstellt. Das mag soweit auch stimmen, problematisch ist nur, dass dies nicht mehr zutrifft, sobald wir etwas anderes als Galvanische Elemente betrachte. Bei der Elektrolyse, ein Konzept, welches wir in einem anderen Skript ausführlich besprechen, stimmt diese Aufteilung beispielsweise nicht mehr. Aus diesem Grund solltest du dir die Definiton merken, die wir hier gegeben haben: Die Anode entspricht dem Ort der Oxidation und die Kathode entspricht dem Ort der Reduktion. Diese Regel ist nämlich immer anwendbar und führt nicht zur Verwirrung!

Räumliche Trennung

Ein sehr wichtiger Aspekt, den du unbedingt im Hinterkopf behalten musst, bezieht sich auf die räumliche Trennung der beiden Elektroden. Eine Spannung kann sich nur dann aufbauen, wenn eine solche räumliche Trennung vorliegt. Das heißt, dass es nicht möglich wäre, die elektrische Energie eines Galvanischen Elements zu nutzen, solange diese räumliche Trennung nicht vorliegt. Wäre diese räumliche Trennung aufgehoben, würde die Redox-Reaktion sofort ablaufen und es könnte sich keine Potentialdifferenz aufbauen, die einen Elektronenfluss möglich machen würde.

Spannungsberechnung

Nun beschäftigen wird uns damit, wie wir die Potentialdifferenz eines Galvanischen Elements berechnen können. Wir haben oben schon die beiden Standardpotential der Redox-Paare gesehen, die am Daniell-Element beteiligt sind:

• 
• 

Die Potentialdifferenz eines Galvanischen Elements bei Standardbedingungen berechnet sich ganz allgemein als:

Wir wollen diese Formel gleich auf das Daniell-Element anwenden. Hier wird Zink oxidiert und da die Oxidation an der Anode abläuft, wissen wir, dass hier das Redox-Paar relevant ist. Demnach setzen wir die Größen für die Standardpotentiale der Redox-Paare ein und erhalten:

Das Daniell-Element weist eine Potentialdifferenz von auf. Da wir diese dazu nutzen können, elektrische Geräte anzutreiben, da eine Potentialdifferenz einen elektrischen Strom hervorruft, wird diese Größe auch elektromotorische Kraft genannt.

Anmerkung: Wenn du dir nicht sicher sein solltest, ob du nicht doch die Anode und die Kathode vertauscht hast, dann schau dir das Vorzeichen deines Ergebnisses an. Solange es positiv ist, ist alles in Ordnung. Sollte es negativ sein, dann musst du die beiden Größen in der Gleichung vertauschen, damit sie richtig wird. Eine negative Potentialdifferenz macht hier nämlich keinen Sinn!

Konzentrationszellen

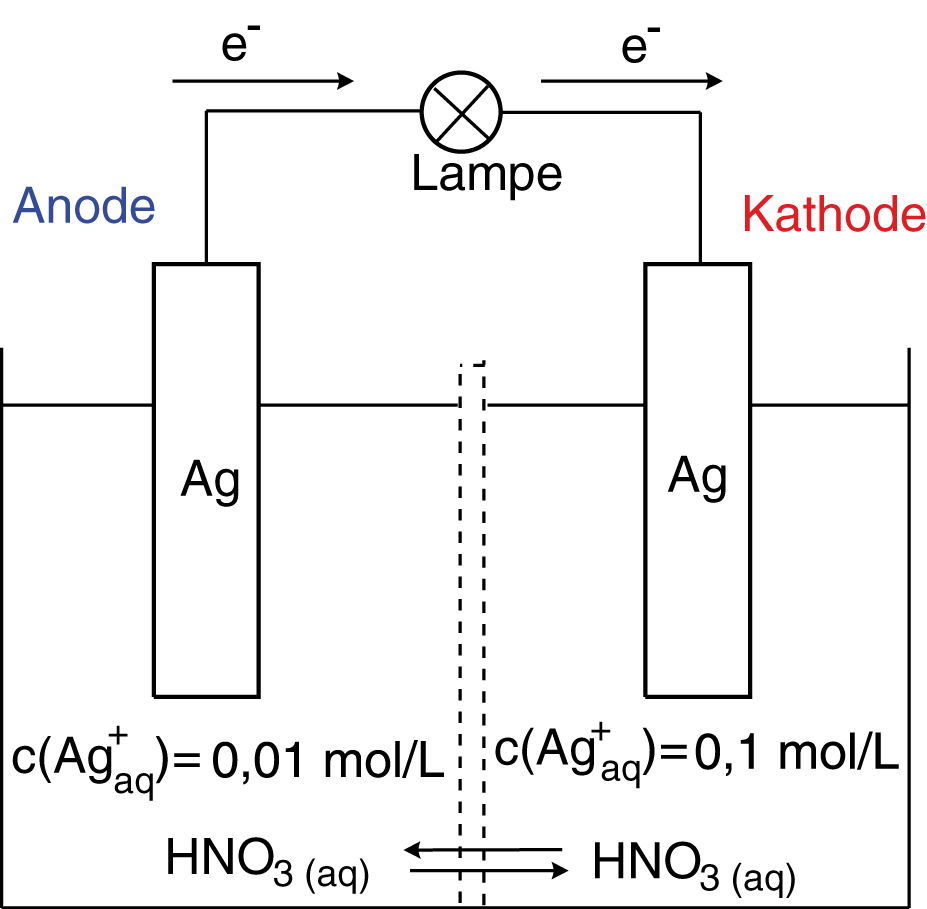
Abschließend wollen wir uns noch um ein weiteres spezielles Galvanisches Element kümmern: Die Konzentrationszelle. Die Konzentrationszelle können wir insbesondere dann gut verstehen, wenn wir die Nernst-Gleichung verwenden, die die Konzentrationsabhängigkeit des Redoxpotentials beschreibt. Folgende Abbildung skizziert den Aufbau einer solchen Zelle:

Eine Konzentrationszelle ist genauso aufgebaut wie jedes andere Galvanische Element, allerdings mit einem großen Unterschied: Hier werden zwei gleiche Halbzellen kombiniert, die sich nur in der Konzentration der jeweiligen Elektrolytlösung ( unterscheiden. Wir wollen nun die Potentialdifferenz bzw. die elektromotorische Kraft dieser Konzentrationszelle berechnen:

Da die Redoxpotentiale in diesem Fall von der Konzentration abhängen, nehmen wir die Nernst-Gleichung zu Hilfe.

Die Anzahl der Elektronen ist in diesem Fall gerade eins (von Ag zu ) und wir betrachten die Konzentrationszelle bei Raumtemperatur, somit können wir den Faktor vor dem „Zehnerlogarithmus“ durch Einsetzen der Zahlenwerte ausrechnen:

Wir können diese Gleichung jetzt für unsere beiden Halbzellen oben einsetzen (weil wir wissen, dass die Redoxpotentiale und von der Konzentration abhängen) und erhalten:

Wichtig ist, dass die reduzierte Form hier einen Feststoff darstellt und die Konzentrationen von Feststoffen sind immer gleich eins. Aus diesem Grund tauchen diese beiden Größen hier nicht mehr auf - der Nenner ist gleich eins. Warum gerade die Halbzelle mit der niedrigeren Elektrolytkonzentration die Donatorhalbzelle und somit die Anode stellt, sehen wir weiter unten. Wenn wir diese Gleichung weiter vereinfachen, dann sehen wir, dass sich die Standardpotentiale gerade gegenseitig aufheben:

Bei diesem Ergebnis kannst du sehen, dass die elektromotorische Kraft eine Konzentrationszelle nicht von den Standardpotentialen des Redox-Paares abhängt (die Größe taucht nicht mehr in der Gleichung für auf), sondern nur vom Konzentrationsverhältnis der beiden Halbzellen. Wenn wir die Zahlenwerte unseres Beispiels von oben einsetzen, erhalten wir:

Damit erhalten wir für ein Konzentrationsverhältnis von 1:10 eine Potentialdifferenz bzw. eine elektromotorische Kraft von . Bevor wir dieses Thema abschließen, schauen wir uns das Prinzip der Konzentrationszelle auch noch auf molekularer Ebene an. Im Zentrum unserer Überlegungen steht die Lösungstension und das chemische Gleichgewicht zwischen Elektrode und Elektrolyt, welches für die elektrische Doppelschicht verantwortlich ist. Die Lösungstension von Silber schreibt diesem Metall die Eigenschaft zu, dass in wässriger Lösung eine gewisse Anzahl an Kationen in Lösung gehen werden.

In unserem Beispiel sagen wir, dass sechs -Kationen diese Anzahl für das chemische Gleichgewicht darstellen. Wir packen jetzt zwei Halbzellen zusammen: die eine im chemischen Gleichgewicht mit dem Elektrolyten, die andere nicht, da viel zu wenig Kationen in Lösung sind (vielleicht nur zwei für unser Beispiel). Die Theorie des chemischen Gleichgewichts sagt uns, dass Gleichgewichtsreaktionen ihrem Gleichgewichtszustand entgegenstreben, da dieser energetisch am günstigsten ist (vgl. Skript Chemische Energetik). Das bedeutet, dass in unserem Fall in der Halbzelle, in der die geringere Konzentration an -Kationen vorherrscht, solche aus dem Elektrodenmaterial in Lösung gehen werden. Somit erhalten wir hier zusätzliche Elektronen in der Elektrode, die in der anderen Halbzelle nicht vorhanden sind: Zwischen beiden Elektroden baut sich eine Potentialdifferenz auf. Das Prinzip der Konzentrationszelle beruht also im Wesentlichen darauf, dass die Konzentrationen des Elektrolyten zu unterschiedlichen Reaktionen der Elektroden führt. In derjenigen mit der geringeren Elektrolytkonzentration, werden mehr Kationen abgegeben und somit wird diese zur Donatorhalbzelle.

Anmerkung: Es ist nicht notwendig, dass die Konzentration einer Halbzelle der Gleichgewichtskonzentration entspricht. Solange ein Konzentrationsunterschied zwischen beiden Elektrolyten besteht, wird eine Elektrode mit einer erhöhten Kationenabgabe reagieren als die andere. Relativ gesehen erhalten wir dann auch eine Potentialdifferenz.