Indikatoren

Einführung

Der Begriff des Indikators kommt von lat. indicare, anzeigen. Damit ist seine Rolle in der Chemie auch schon sehr gut beschrieben: Indikatoren sind Hilfsmittel um beispielsweise den pH-Wert einer Lösung visuell darzustellen. Durch spezifische pH-Wert abhängige Farbänderungen erlauben es Indikatoren zum Beispiel pH-Wert-Änderungen sichtbar zu machen.
Wir wollen uns in diesem Kapitel mit dem Aufbau von Indikatoren beschäftigen und bereits ihre Anwendung andeuten. Letztere werden wir dann im letzten Kapitel des Basiswissens Säure-Base-Gleichgewichte: Anwendungen-Titration umfangreich besprechen.

Wir werden uns in diesem Basiswissen auf Indikatoren konzentrieren, die auf pH-Wert Änderungen reagieren: sogenannte pH-Indikatoren. Daneben gibt es aber auch noch in anderen Bereichen der Chemie Indikatoren. Im Folgenden findest du eine kleine Übersicht:

Redox-Indikatoren: finden Verwendung bei Redox-Titrationen; dabei laufen primär keine Säure-Base-Reaktionen ab, sondern Redox-Reaktionen. Das Vorgehen ist jedoch prinzipiell dasselbe.
Komplex-Indikatoren: finden bei einem Verfahren namens Komplexometrie Verwendung. Dabei werden Metallkationen mithilfe eines Komplexbildners in eine Komplexverbindung überführt.

Aufbau von pH-Indikatoren

Wir wollen uns an dieser Stelle die Funktionsweise von pH-Indikatoren genauer anschauen, also welche Substanzen geeignet sind und was passiert, wenn sie zum Einsatz kommen.

Ein Indikator besteht aus einer schwachen Säure und deren korrespondierenden Base!

Diese Kombination kommt dir sicher von den Puffersystemen bekannt vor. Das bedeutet, dass wir auch für Indikatoren die Henderson-Hasselbalch-Gleichung heranziehen können. Zunächst wollen wir uns jedoch einen solchen Indikator anschauen: dazu nennen wir die schwache Indikatorsäure HInd und ihre korrespondierende Base Ind $^{-}$ .

Das Säure-Base-Gleichgewicht kann dann wie folgt formuliert werden:

$\text{HInd}+\text{H}_{2}\text{O}$ $\rightleftharpoons$ $\text{Ind}^{-}+\text{H}_{3}\text{O}^{+}$

Die Funktion von Indikatoren beruht darauf, dass die protonierte Indikatorsäure HInd eine andere Farbe aufweist, als ihre korrespondierende Base Ind $^{-}$ .
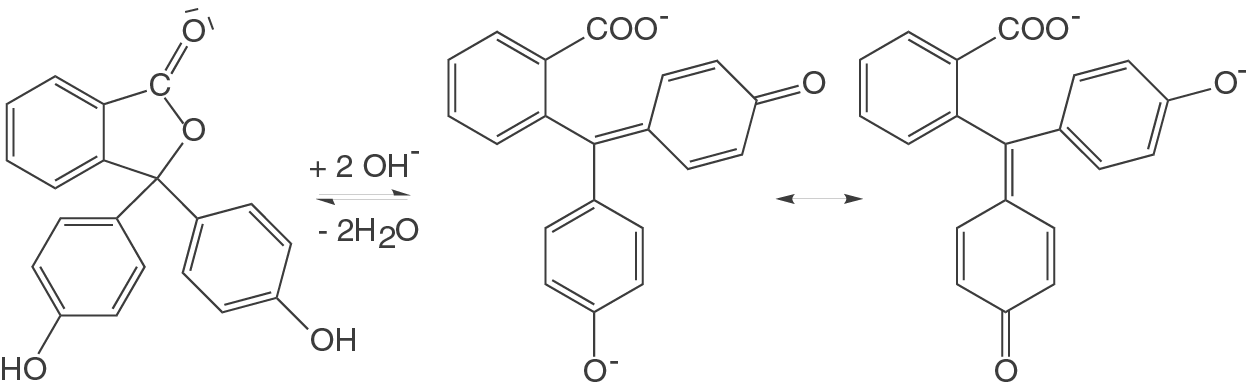
Im folgenden Beispiel kannst du das Gleichgewicht zwischen der protonierten und der deprotonierten Form des bekannten Indikators Phenolphthalein sehen:

Chemische Strukturformel mit Reaktionen und Hydroxidionen.

Abb. 1: Basenreaktion von Phenolphtalein

Auf der linken Seite siehst du die protonierte Version des Indikators (analog zu HInd aus unserem Beispiel). Diese ist farblos und liegt im Bereich von niedrigen pH-Werten vor. In dem Fall sind viele $\text{H}_{3}\text{O}^{+}$ -Ionen in der Lösung und somit sind alle Sauerstoffatome protoniert.
Auf der rechten Seite des Gleichgewichts siehst du die mesomeren Grenzformeln der deprotonierten Indikatorsäure (analog zu Ind $^{-}$ aus unserem Beispiel). Diese weist eine rote Farbe auf und liegt im Fall von hohen pH-Werten vor.

Der Farbumschlag

Im oberen Abschnitt haben wir gesehen, dass die beiden Komponenten des Indikators unterschiedliche Farben aufweisen. Damit wir also sehen können welcher pH-Wert vorliegt, benötigen wir insbesondere eine der beiden Komponenten im Überschuss. Dann hat die Lösung eine deutlich Farbe, die wir einem pH-Wert Bereich zuordnen können.
Wir wollen an dieser Stelle nun auf die Theorie aus dem Kapitel Puffersysteme zurückgreifen, um so den Umschlagsbereich des Indikators genauer zu bestimmen. Dazu verwenden wir wie oben angekündigt die Henderson-Hasselbalch-Gleichung mit folgenden Änderungen:

$c(\text{HAc}) = c(\text{HInd})$
$c(\text{Ac}^{-}) = c(\text{Ind}^{-})$

$\text{pH}$ = $\text{pK}_{\text{S}}+\lg\left(\dfrac{c(\text{Ind}_{(\text{aq})}^{-})}{c(\text{HInd}_{(\text{aq})})}\right)$

Der $\text{pK}_{\text{S}}$ -Wert ist hier derjenige der Indikatorsäure HInd. Der Umschlagspunkt ist der, an welchem die Farbänderung eintritt. In diesem Zustand ist die Konzentration von HInd und Ind $^{-}$ gleich: $c(\text{Ind}_{(\text{aq})}^{-})=c(\text{HInd}_{(\text{aq})})$ .
Dafür erhalten wir das analoge Ergebnis wie beim Pufferpunkt eines Puffersystems:

$\text{pH}$ = $\text{pK}_{\text{S}}$

$\lg\left(\dfrac{c(\text{Ind}_{(\text{aq})}^{-})}{c(\text{HInd}_{(\text{aq})})}\right)$ = $\lg\left(\dfrac{c(\text{HInd}_{(\text{aq})})}{c(\text{HInd}_{(\text{aq})})}\right)$ = $\lg(1)$ = $0$

Das bedeutet, dass der Umschlagspunkt eines Indikators auf den $\text{pK}_{\text{S}}$ -Wert der Indikatorsäure zurückzuführen ist. Eine deutliche Färbung erhalten wir aber erst dann, wenn eine der beiden Formen des Indikators (je nach pH-Wert) im Überschuss vorliegt. Das heißt, dass wir zwar von einem Umschlagspunkt reden können, aber im Endeffekt den Bereich des Umschlags festlegen müssen. Der Umschlag verläuft zwar oft sehr plötzlich, aber nicht schlagartig sondern über einen bestimmten Konzentrationsbereich der beiden farbgebenden Indikatorkomponenten.
Wir wollen folgende Annahmen treffen, um eine reine Farbe des Indikators sicher vorliegen zu haben:

pH $>\text{pK}_{\text{S}}$ : Verhältnis c(HInd) zu c(Ind $^{-}$ ) in der Lösung entspricht 1:10.
pH $<\text{pK}_{\text{S}}$ : Verhältnis c(HInd) zu c(Ind $^{-}$ ) in der Lösung entspricht 10:1.

Das bedeutet, dass wir unseren Umschlagsbereich so eingrenzen, dass die obere Grenze dort liegt wo die Konzentration an Ind $^{-}$ die Konzentration der Indikatorsäure HInd um das 10-fache übersteigt und die untere Grenze dort, wo die Konzentration der Indikatorsäure HInd die Konzentration der korrespondierenden Base Ind $^{-}$ um das 10-fach übersteigt.Diesen pH-Wert Bereich bezeichnen wir mit $\Delta\text{pH}$ :

$\Delta\text{pH}$ = $\text{pH}_{\text{oben}}-\text{pH}_{\text{unten}}$

Mit $\text{pH}_{\text{oben}}$ bezeichnen wir den pH-Wert für den das folgende Mischungsverhältnis vorliegt:

$\dfrac{c(\text{Ind}^{-})}{c(\text{HInd})}$ = $\dfrac{10}{1}$ und pH $>\text{pK}_{\text{S}}$

Analog sagen wir für den unteren pH-Wert $\text{pH}_{\text{unten}}$ :

$\dfrac{c(\text{Ind}^{-})}{c(\text{HInd})}$ = $\dfrac{1}{10}$ und pH $<\text{pK}_{\text{S}}$

Nun verwenden wir die Henderson-Hasselbalch-Gleichung zur Berechnung der beiden pH-Werte:

(1.) $\text{pH}_{\text{oben}}$

$\begin{array} \text{pH}_{\text{oben}} \\ = \text{pK}_{\text{S}}+\lg\left(\dfrac{c(\text{Ind}_{(\text{aq})}^{-})_{\text{oben}}}{c(\text{HInd}_{(\text{aq})})_{\text{oben}}}\right) \\ = \text{pK}_{\text{S}}+\lg\left(\dfrac{10}{1}\right) \end{array}$

(2.) $\text{pH}_{\text{unten}}$

$\begin{array} \text{pH}_{\text{unten}} \\ = \text{pK}_{\text{S}}+\lg\left(\dfrac{c(\text{Ind}_{(\text{aq})}^{-})_{\text{unten}}}{c(\text{HInd}_{(\text{aq})})_{\text{unten}}}\right) \\ = \text{pK}_{\text{S}}+\lg\left(\dfrac{1}{10}\right) \end{array}$

Durch Einsetzen können wir unseren pH-Wert-Bereich $\Delta\text{pH}$ berechnen.

$\begin{array}{rcl} \Delta\text{pH} &=& 2 \end{array}$

Vollständige Lösung anzeigen

Der Umschlagsbereich umfasst demnach zwei pH-Einheiten: $\Delta\text{pH}=2$ . Das bedeutet, dass du bei Indikatoren im Bezug auf ihren Anwendungsbereich auch immer auf diesen Umschlagsbereich achten musst.

Bildnachweise [nach oben]

[1]