Entropie

Hinführung zum Entropiebegriff

Wichtig:

Wir werden uns in diesem Skript des Basiswissens ChemieLV mit dem Begriff der Entropie beschäftigen. In diesem Zusammenhang treten im Unterricht insbesondere zwei Begriffe sehr häufig auf: Wahrscheinlichkeit und Unordnung. An dieser Stelle wollen wir versuchen die Größe der Entropie mit diesen Begriffen zusammen zu bringen und so ansatzweise zu verstehen. Da der Begriff der Entropie oft sehr unzugänglich erscheint, wird dieses Skript an einigen Stellen den Schulstoff übersteigen. Für ein erfolgreiches Abitur in Chemie wirst du demnach nicht alles in diesem Skript benötigen.

Spontane Reaktionen - Die Richtung freiwilliger Prozesse

Bevor wir den Begriff der Entropie einführen, müssen wir noch eine gewisse Vorarbeit leisten. Dazu beginnen wir mit dem Begriff der spontanen Reaktion in isolierten Systemen (kein Stoff- und Energieaustausch mit der Umgebung). Im Alltag kennen wir viele Situationen, in welchen bestimmte Prozesse nur in eine Richtung ablaufen. Eine Tasse Kaffee bzw. ein warmer Körper im Allgemeinen wird sich im Lauf der Zeit auf Raumtemperatur abkühlen. Ein Gas wird sich in einem Volumen solange ausbreiten, bis es gleichmäßig verteilt ist.
Gleichzeitig kennen wir aber auch Situationen, in welchen Prozesse umkehrbar sind. Wir können Eis auftauen und es anschließend wieder einfrieren. Was wir hier jedoch nicht beobachten können, ist, dass das flüssige Wasser ohne unser Zutun bei Raumtemperatur von alleine wieder gefriert. Das heißt, dass die andere Richtung nur durch einen äußeren Zwang möglich wird.

Abb. 1: Freiwillig und unfreiwillig ablaufende Prozesse

Wir können demnach zwei Gruppen von Reaktionen bilden: Reaktionen, die freiwillig ablaufen und Reaktionen, die nicht freiwillig ablaufen. Im Bezug auf die Unumkehrbarkeit einer Reaktion, wird auch der Begriff irreversibel verwendet.

Der 2. Hauptsatz der Thermodynamik

Der 2. Hauptsatzes der Thermodynamik bringt die Tatsache, dass es diese zwei Gruppen gibt, die wir im letzten Abschnitt gefunden haben, zum Ausdruck.
Er lautet:

Ein Prozess, bei welchem Wärme aus einem Reservoir entnommen wird und vollständig in Arbeit umgewandelt wird, ist nicht möglich.

Wir wollen den Inhalt anhand eines alltäglichen Beispiels verstehen. Es wird darum gehen, dass ein Ball nie von alleine vom Boden in die Luft springen würde.

Wir betrachten ein isoliertes System und werfen einen Ball, dieser fällt auf den Boden und hüpft ein paar Meter weiter.

Abb. 2: Umwandlung von Energie

Wenn der Ball auf den Boden auftrifft, wird seine kinetische Energie in Wärmeenergie des Bodens umgewandelt. Der Boden wird also minimal wärmer, weil die Atome und Moleküle in Bewegung geraten. Ist die gesamte kinetische Energie in Wärmeenergie umgewandelt worden, dann bleibt der Ball liegen. In dieser Situation können wir folgendes beobachten: Anfänglich hatten wir ein geordnetes System. Der Ball hatte einen gewissen Betrag an kinetischer Energie und der Boden einen Betrag an thermischer Energie. Diese Energie ist am Ende des Prozesses im System gleichmäßig in Form von Wärmeenergie umverteilt worden. Die anfängliche Ordnung ist demnach einem gewissen Grad an Unordnung gewichen: es liegt keine klare Trennung verschiedener Energiebeträge mehr vor! Die Gesamtenergie des Systems ist erhalten aber wir haben die bereits erwähnte Umverteilung der Energie. Wichtig ist, dass dieser Prozess spontan abläuft und ohne einen äußeren Zwang unumkehrbar (irreversibel) ist. Bevor wir nun daran gehen, diese Beobachtung auszuwerten, schauen wir uns die andere Variante an.

Eine Umkehr dieses Prozesses, also dass der Ball von alleine vom Boden hoch springt, ohne dass wir in irgendeiner Art und Weise von außen eingreifen, werden wir nicht beobachten können.

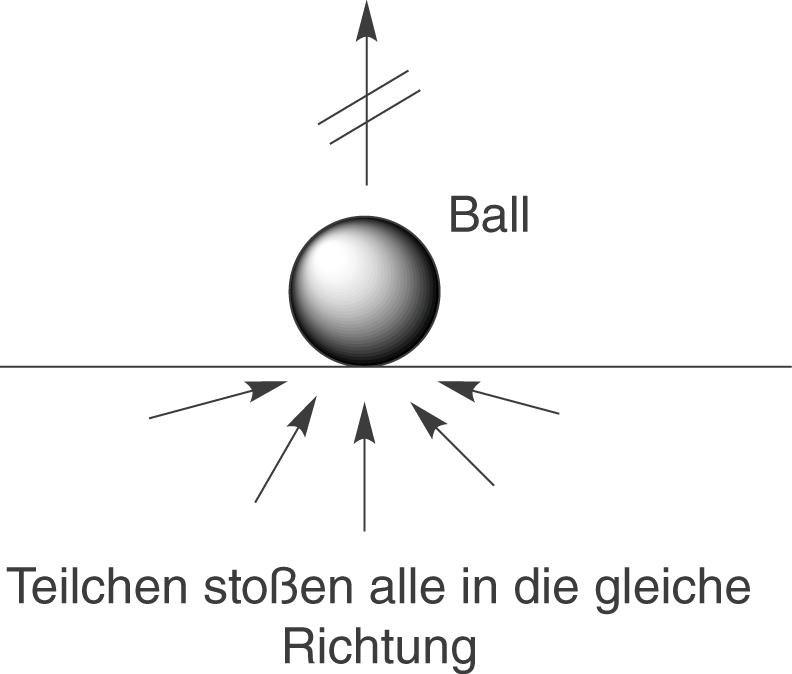
Damit wir das beobachten könnten, müsste folgendes geschehen: Die gleichmäßig verteilte thermische Energie des Bodens müsste sich räumlich konzentrieren. Das kannst du dir so vorstellen, dass alle Teilchen Stöße in die gleiche Richtung ausführen müssten, um den Ball in die Luft zu befördern. Die Graphik rechts veranschaulicht dieses unmögliche Beispiel.

Abb. 3: Der Ball springt nicht von selbst

Wir wollen nun zusammenfassen, was wir bisher herausgefunden haben:

In isolierten Systemen ist die Richtung eines Prozesses bevorzugt, die zu einer Gleichverteilung der Energie des Systems führt. Der Prozess läuft in diese Richtung spontan und irreversibel ab.
Die Energie des isolierten Systems ist nach dem Energieerhaltungssatz erhalten.

Nun können wir auf den 2. Hauptsatz der Thermodynamik zurückkommen und diesen im Zusammenhang mit dem zweiten, dem unwahrscheinlichen, Beispiel erklären. Um den Ball wieder in die Luft zu befördern, muss am Ball die Arbeit $W$ verrichtet werden. Im Skript Energie haben wir Arbeit als Energiemenge, die bei einem Prozess umgesetzt wird, bezeichnet. Diese Energiemenge muss demnach aus einer anderen Quelle stammen, welche in unserem Fall die thermische Energie $Q$ des Bodens ist. Was uns der 2. Hauptsatz der Thermodynamik sagt, ist, dass es eben nicht möglich ist, dass ein Energiebetrag der Wärmeenergie $Q$ des Bodens komplett dafür aufgewendet werden kann, dass der Ball wieder in die Luft fliegt (das an dem Ball die Arbeit $W$ verrichtet wird).

Prinzipiell gilt es also folgendes zu klären:

Welche Richtung eines Prozesses ist die spontane (irreversible)?
Welches Kriterium können wir heranziehen, um die erste Frage zu beantworten?

Die Entropie $S$

Definition

Das oben gesuchte Kriterium, welches uns erlaubt die freiwillige Richtung eines Prozesses zu finden, nennen wir Entropie und bezeichnen es mit dem Formelzeichen $S$ .

Für isolierte Systeme gilt dabei folgendes:

$\Delta S>0$

Bei einer irreversiblen Zustandsänderung nimmt die Entropie des isolierten Systems zu.

$\Delta S=S_{2}-S_{1}>0\hspace{.4cm}\text{und}\hspace{.4cm}S_{2}>S_{1}$

Die Entropie wird im Endzustand ( $S_{2}$ ) immer größer sein, als im Anfangszustand ( $S_{1}$ ).

Entropie und Unordnung

Wir haben nun die Begriffe der irreversiblen Prozesse und der Entropie kennen gelernt. Nun können wir dazu übergehen auch den Begriff der Unordnung mit einzubeziehen.

Wir betrachten auch weiterhin ein isoliertes System. In Abschnitt 1.2. habe wir herausgefunden, dass die Energie in einem isolierten System erhalten ist, ihre Verteilung sich aber ändern kann.
In isolierten Systemen sind die Prozesse bevorzugt, die zu einer Gleichverteilung der Energiebeträge im System führen. Je ausgeprägter diese Gleichverteilung, desto größer ist auch die Änderung der Entropie $\Delta S$ des Systems.
An dieser Stelle können wir nun den Begriff der Unordnung mithilfe der folgenden Metapher einführen: Stelle dir ein ordentliches Zimmer vor. Alles hat seinen Platz; die einzelnen Bestandteile sind geordnet und manche Plätze sind stärker beansprucht als andere. Beispielsweise befinden sich alle Bücher im Schrank und die Bausteine in einer Kiste. Es gilt nun folgende Frage zu beantworten: Wie wird sich der Zustand dieses Zimmers ändern, wenn du nicht die Energie aufbringst, um aufzuräumen?.
Die Bücher werden langsam aber sicher überall im Zimmer verteilt werden, weil du im Lauf der Zeit jedes aus dem Schrank nehmen wirst und nicht wieder zurückstellst. Die Bauklötze werden sich gleichmäßig auf dem Boden verteilen.

Nun ziehen wir die Verbindungen zur Entropie: Die Energie wird in isolierten Systemen durch irreversible Prozesse gleichverteilt. Das gleiche geschieht im Lauf der Zeit mit den Utensilien in deinem Zimmer: alles wird über den gesamten Raum verteilt. Wir nennen diesen Zustand Unordnung die Entropie nimmt zu. Ganz analog kannst du dir die Gleichverteilung der Energie vorstellen. In unserem Beispiel in Abschnitt 1.2. waren die Energiebeträge anfänglich auf den Ball und den Boden aufgeteilt. Wir hatten eine gewisse Ordnung im System. Ein irreversibler Prozess hat dazu geführt, dass der Ball nach mehrmaligem aufspringen zum Liegen kam und seinen Energiebetrag an die Umgebung abgegeben hat. Letztlich lag die anfängliche Ordnung nicht mehr vor und wir können davon sprechen, dass die Unordnung in einem gewissen Maß zugenommen hat: die Entropieänderung war positiv.

Merke:
In isolierten Systemen ist die Entropieänderung immer positiv. Eine Zunahme der Entropie des Systems ist als eine Gleichverteilung der Energie des Systems zu verstehen. Trotzdem ist die Energie nach dem EES erhalten. Diese angestrebte Gleichverteilung der Energie in isolierten Systemen können wir als Zunahme der Unordnung im System beschreiben.

Der 3. Hauptsatz der Thermodynamik

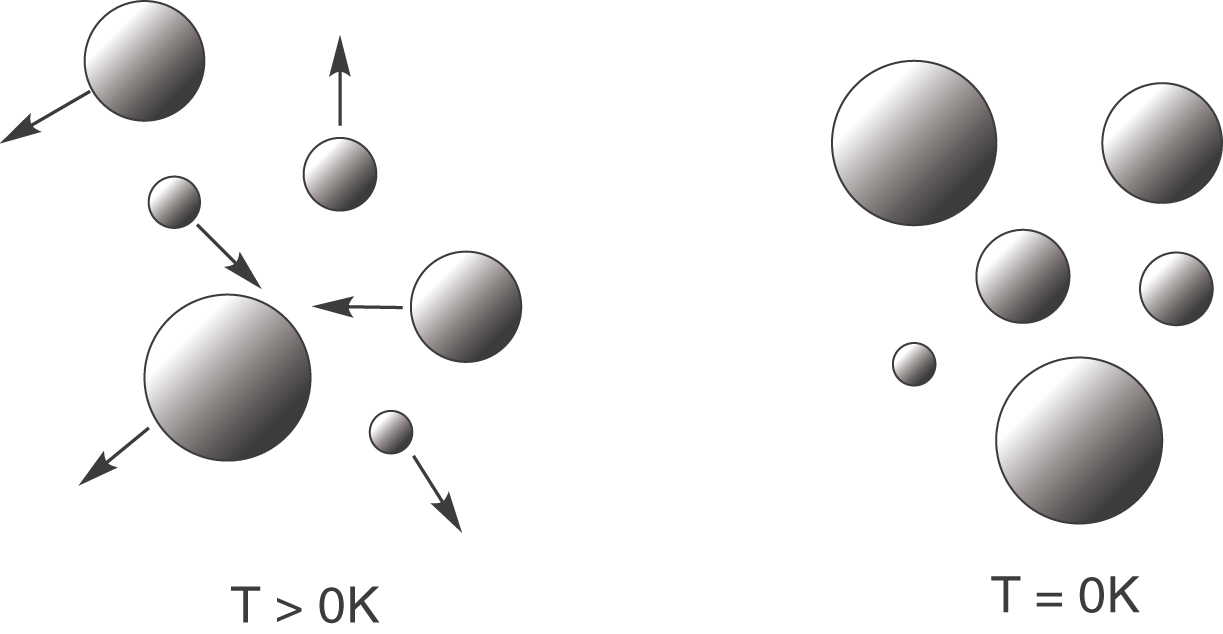
Der 3. Hauptsatz der Thermodynamik beruht darauf, dass es einen Temperaturnullpunkt ( $T=0\,\text{K}=-273,15\text{°}\,\text{C}$ ) gibt, an welchem die Teilchen keine thermischen Bewegungen mehr ausführen.

Abb. 4: Teilchenbewegung

Links siehst du Teilchen, die sich immer noch bewegen, da $T>0\,\text{K}$ . Rechts ist $T=0\,\text{K}$ und die Teilchen bewegen sich nicht mehr. Im rechten Fall spricht man auch von einem idealen Kristall, da alle Teilchen in diesem Zustand in einem starren Gitter angeordnet sind. Vor diesem Hintergrund lautet die Formulierung des 3. Hauptsatz der Thermodynamik: Die Entropie aller ideal kristallinen Stoffe ist bei $\boldsymbol{T=0\,\text{K}}$ null.
Diese Behauptung erscheint auf den ersten Blick etwas willkürlich. Dass diese Überlegung aber gerechtfertigt ist, werden wir im letzten Abschnitt Entropie und Wahrscheinlichkeit dieses Skripts sehen. Doch zunächst zu den Vorteilen, welche uns diese Definition liefert.
üenn die Entropie von der Temperatur abhängt, also $S=f(t)$ und am absoluten Temperaturnullpunkt ( $T=0\,\text{K}=-273,15\text{°}\,\text{C}$ ) für die Entropie $S(T=0)=0$ gilt, dann können wir uns auch überlegen welche Entropie eine Verbindung bei Standardbedingungen ( $T=298\,\text{K}=25\text{°}\,\text{C}$ ) hat. Wenn wir diese Größe dann auch noch auf die Stoffmenge von einem Mol dieser betrachteten Verbindung beziehen, können wir uns die molare Standardentropie $S^{0}_{\text{m}}$ definieren.
Die Einheit der molaren Standardentropie $S^{0}_{\text{m}}$ ist: $\left[S^{0}_{\text{m}}\right]$ = $\dfrac{\text{J}}{\text{K}\cdot\text{mol}}$ .
Beachte hierbei das Joule im Zähler steht und nicht Kilojoule!
Vielleicht erinnerst du dich hier an die molare Standardbildungsenthalpie, welche wir im Skript Enthalpie besprochen haben. Analog zu dieser können wir nämlich mithilfe der molaren Standardentropie auch eine molare Standardreaktionsentropie berechnen, die wir $\Delta_{\text{R}}S^{0}_{\text{m}}$ nennen wollen. Die molare Standardreaktionsentropie lässt sich wie folgt berechnen:

$\Delta_{\text{R}}S^{0}_{\text{m}}$ = $\displaystyle\sum b\cdot S^{0}_{\text{m}}(\text{Produkte})$ - $\displaystyle\sum b\cdot S^{0}_{\text{m}}(\text{Edukte})$

Dabei steht der Faktor $b$ für die stöchiometrischen Koeffizienten, die in der betrachteten Reaktion auftreten.

Merke:
Molare Standardentropien von Elementen sind ungleich null! Die Entropie einer Verbindung ist nur am Temperaturnullpunkt gleich null. Verwechsle das nicht mit der molaren Standardbildungsenthalpie.

Beispiel: Entropieänderung bei der Knallgasreaktion unter Standardbedingungen
Wir betrachten folgende Reaktion:
Die Werte für die molare Standardentropien der beteiligten Verbindungen kannst du einem Tabellenwerk entnehmen. Nun können wir die molare Standardreaktionsentropie berechnen:

$\begin{array}{rcl} \Delta_{\text{R}}S^{0}_{\text{m}} &=& -163,3\,\frac{\text{J}}{\text{K}\cdot\text{mol}} \end{array}$

Vollständige Lösung anzeigen

Die Entropieänderung ist in diesem Fall negativ, dass heißt kleiner als null: $\Delta_{\text{R}}S^{0}_{\text{m}}<0$ . Bisher hatten wir es immer nur mit positiven Entropieänderungen zu tun. Im Vergleich zu dem, was wir bisher erarbeitet haben, müssen wir jetzt die folgenden zwei Punkte beachten:

Wir müssen immer das System betrachten, in welchem eine Reaktion stattfindet. In einem isolierten System (kein Stoff- und Energieaustausch mit der Umgebung) würden wir diese Reaktion nach dem 2. Hauptsatz der Thermodynamik nicht beobachten können.
Ganz allgemein kann die Entropie bei Reaktionen auch abnehmen. Dies ist insbesondere dann der Fall, wenn gasförmige Stoffe wie hier in der Reaktion verbraucht werden. Die Ordnung in einem System ändert sich mit dem Aggregatzustand und nimmt von gasförmig über flüssig nach fest zu.

Die Frage, die wir laut dieser beiden Aspekte klären müssen ist: Ist die Entropieänderung einer Reaktion im betrachteten System nach dem 2. Hauptsatz der Thermodynamik möglich? Diese Frage wollen wir im nächsten Abschnitt näher beleuchten.

Entropieänderungen in geschlossenen Systemen

Wir habe gerade gesehen, dass die Entropieänderung im Falle der Standardreaktionsentropie laut unserer Berechnung auch negativ sein kann. In diesem Kapitel wollen wir uns mit geschlossenen Systemen beschäftigen und uns fragen, welche Entropieänderungen sich in diesen Systemen mit dem 2. Hauptsatz der Thermodynamik vereinbaren lassen und worin der entscheidende Unterschied zu den bis jetzt betrachteten isolierten Systemen liegt.

Ist das System isoliert, dann sagt uns der 2. Hauptsatz der Thermodynamik, dass $\Delta S>0$ . Das System gibt somit die Randbedingungen vor und die Knallgasreaktion wird nicht ablaufen.
Würde es das System jedoch auf irgendeine Weise zulassen, dass die Entropieänderung negativ sein kann, dann würde die Knallgasreaktion ablaufen. Und das ist ja auch unsere Erfahrung aus dem Alltag. Die Knallgasreaktion ist möglich.

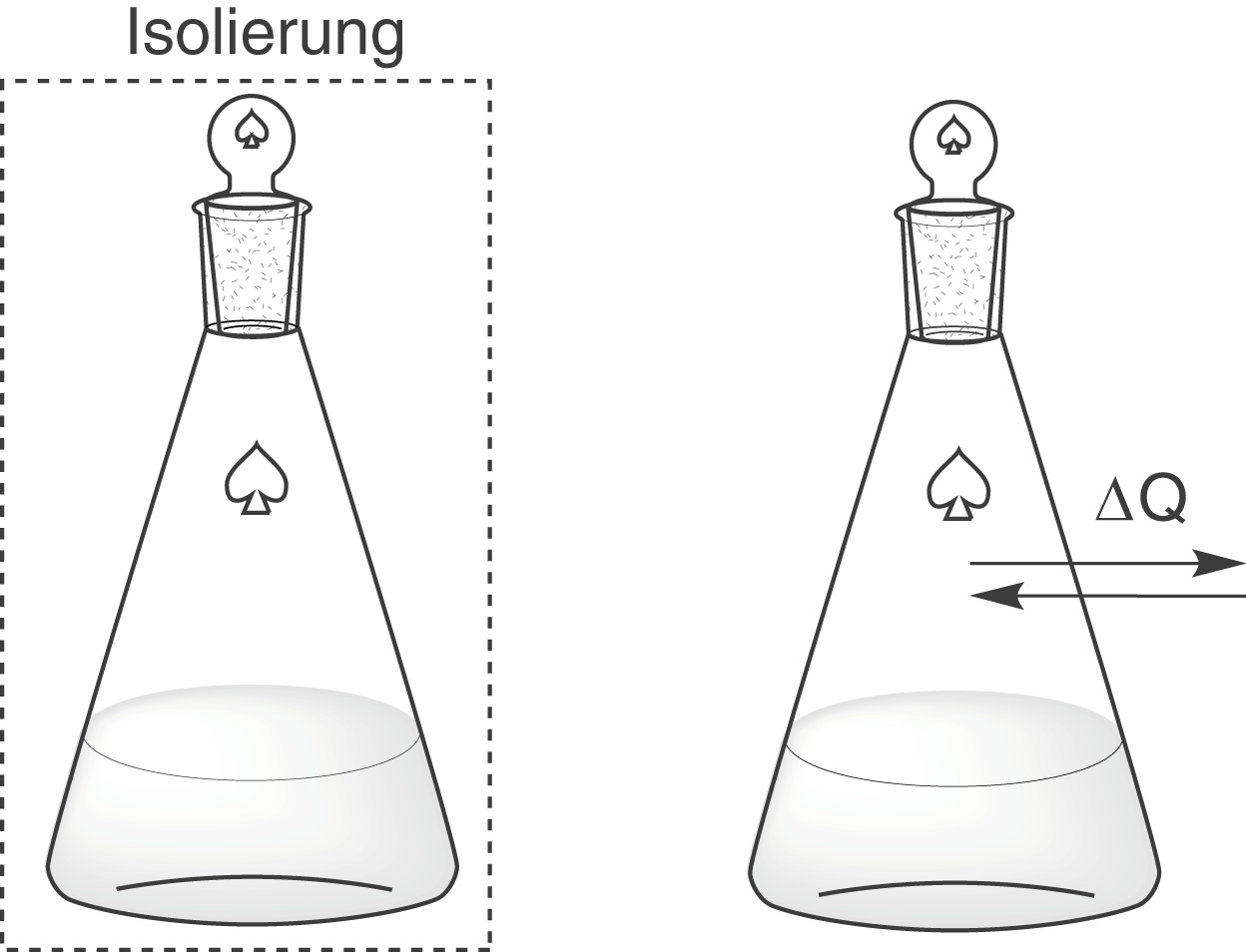
Unser Augenmerk liegt in diesem Kapitel auf dem zweiten Aspekt. Dazu verlassen wir das isolierte System und begeben uns ab sofort in ein geschlossenes System. Weil diese Tatsache so wichtig ist, führen wir uns hier noch einmal den Unterschied vor Augen:

Abb. 5: Isoliertes und geschlossenes System

Links siehst du das isolierte System. Hier sind weder Stoff- noch Energieaustausch mit der Umgebung möglich. Rechts siehst du hingegen das geschlossene System. Hier ist ein Energieaustausch $\Delta Q$ mit der Umgebung möglich. Das bedeutet, dass wir im Vergleich zu den isolierten Systemen bei den geschlossenen Systemen auch deren Umgebung betrachten müssen. Wir können nun die gesamte Entropieänderung $\Delta S_{\text{gesamt}}$ , also vom geschlossenen System und seiner Umgebung, als Summe von zwei Entropieänderungen schreiben.

$\Delta S_{\text{gesamt}}$ = $\Delta S_{\text{System}}+\Delta S_{\text{Umgebung}}$ $\gt 0$

Wir schauen uns nun zwei Fälle an, die im Falle von Reaktionen auftreten können, die in einem geschlossenen System ablaufen:

Die Entropieänderung im geschlossenen System ist positiv. Nimmt die Entropie im System zu, dann wird sie das auf Kosten der Entropie der Umgebung tun. Eine Begründung sehen wir weiter unten.
Die Entropieänderung im geschlossenen System ist negativ. In diesem Fall muss die Entropie der Umgebung zunehmen.

Eine höhere Entropie kommt insbesondere dann Zustande, wenn sich die Temperatur erhöht, denn wir haben gesehen, dass die Entropie von der Temperatur abhängt: $S=f(T)$ . Der Knackpunkt an der Sache liegt darin begründet, dass ein Energieaustausch $\Delta Q$ mit der Umgebung möglich ist.
Wir ziehen hier noch einmal das Beispiel der Knallgasreaktion heran: Wie wir wissen verläuft diese Reaktion stark exotherm. Das bedeutet, dass bei der Umsetzung von elementarem Wasserstoff und Sauerstoff große Mengen an Wärmeenergie $\Delta Q$ frei werden. Wenn wir nun ein geschlossenes System betrachten, dann kann diese Wärmeenergie $\Delta Q$ über die Systemgrenzen hinweg mit der Umgebung ausgetauscht werden. Nur so ist die negative Entropieänderung, also die Verringerung der Entropie im geschlossenen System überhaupt möglich: Die Entropie des geschlossenen Systems nimmt auf Kosten der Entropie seiner Umgebung ab. Im anderen Fall würde Wärmeenergie $\Delta Q$ aus der Umgebung in das geschlossene System aufgenommen werden, was dann eine Entropieerhöhung im System zur Folge hätte: Die Entropie des geschlossenen Systems nimmt also auch auf Kosten der Entropie der Umgebung zu.
Eine Entropieänderung in einem geschlossenen System ist folglich auch immer mit einer Entropieänderung in dessen Umgebung verbunden. Insgesamt kann ein Prozess nur dann ablaufen, wenn auch die Änderung der Gesamtentropie positiv ist.

Entropie und die thermodynamische Wahrscheinlichkeit

Im letzten Abschnitt wollen wir einen Blick auf den Zusammenhang zwischen der Entropie und dem Wahrscheinlichkeitsbegriff werfen.

Wichtig:
Die thermodynamische Wahrscheinlichkeit hat nichts mit dem mathematischen Wahrscheinlichkeitsbegriff zu tun. Letzterer beschreibt das Verhältnis von günstigen zu möglichen Fällen eines Ereignisses. Diese Argumentation macht im Kontext zur Entropie aber keinen Sinn, deshalb schauen wir uns diese thermodynamische Wahrscheinlichkeit im Folgenden auch etwas genauer an.

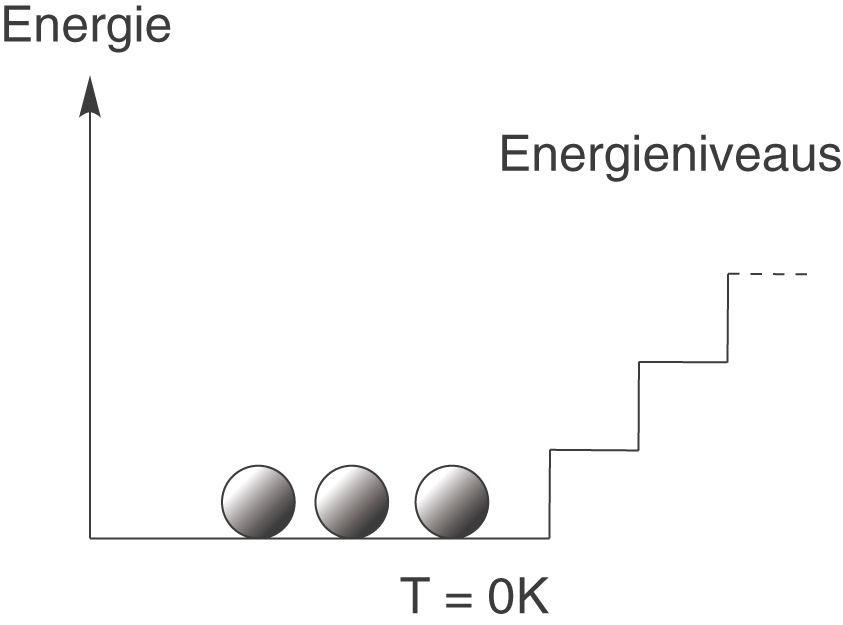
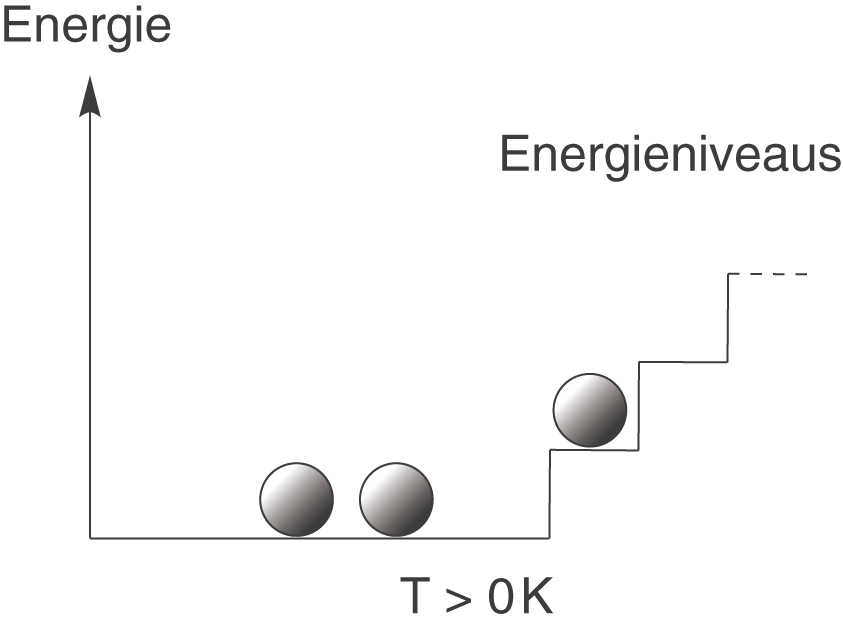
Diese statistische Deutung der Entropie beruht auf einer mikroskopischen Betrachtung, das heißt, dass wir uns auf die atomare Ebene begeben und Gruppen von Atomen betrachten. Wir wollen damit beginnen, dass jedes Atom am Temperaturnullpunkt ( $T=0\,\text{K}$ ) genau den gleichen Energiebetrag besitzt. Zur Veranschaulichung dient die folgende Graphik:

Abb. 6: Grundzustand

Alle Atome befinden sich hier im so genannten energetischen Grundzustand, d.h. du kannst dir vorstellen, dass sie alle auf der untersten Stufe der Treppe sitzen. Ganz wichtig ist hierbei, dass diese Besetzung genau so bleibt, solange sich die Temperatur nicht ändert.
Wenn wir die Temperatur nun erhöhen, dann werden auch die Atome beeinflusst. Ein paar von ihnen werden dann beispielsweise eine „Stufe“ auf der Treppe nach oben steigen. Die dazu nötige Energie liefert die höhere Temperatur.

Abb. 7: Anregung

Erhöhen wir die Temperatur weiter, dann werden auch weitere Atome in diese angeregten Zustände „aufsteigen“.

Abb. 8: Eine höhere Temperatur führt zu einer stärkeren Anregung von mehr Teilchen

Wichtig ist, dass bei einer bestimmten Temperatur $T$ mit $T>0\,\text{K}$ die Anordnung dieser Besetzung festgelegt ist. Das bedeutet, dass es bei jeder konstanten Temperatur für jede Stufe eine festgelegte Anzahl an Atomen gibt, die auf ihr sitzen (die diesen Energiebetrag besitzen). Diese charakteristische Anordnung, die für jede Temperatur spezifisch ist, nennen wir den Makrozustand des Systems. Die Anzahl an Atomen, die auf den Stufen sitzen, nimmt mit zunehmender besetzter Stufenanzahl ab. Das heißt, es gibt sehr viel weniger Atome, die hohe Energien besitzen (auf hohen Stufen sitzen) als niedrige. Die Gesamtenergie des betrachteten Systems umfasst dabei alle Energiebeträge der verschiedenen Atome.

Nun kommen wir zum Zusammenhang zur Entropie. Der österreichische Physiker Ludwig Boltzmann fand folgende Gleichung:

$S=k_{\text{B}}\cdot\ln(W)$

$S$ ist dabei die absolute Entropie, $k_{\text{B}}$ die Boltzmann-Konstante, $\ln$ der „Zweierlogarithmus“ und $W$ die thermodynamische Wahrscheinlichkeit oder auch die Anzahl der Mikrozustände. Wichtig ist, dass wir mit dieser Formel keine Entropieänderung $\Delta S$ berechnen, sondern den absoluten Entropiewert $S$ des betrachteten Systems.

Der 3. Hauptsatz der Thermodynamik sagt uns, dass die Entropie am Temperaturnullpunkt gleich null ist. Wir betrachten nun die erste Graphik in diesem Abschnitt: alle Atome sitzen bei $T=0\,\text{K}$ auf der untersten Stufe. Das bedeutet es gibt genau eine Möglichkeit diesen Mikrozustand zu erreichen. Damit ist $W=1$ . Wenn wir das nun in die Boltzmann-Gleichung einsetzen, bekommen wir:

$S$ = $k_{\text{B}}\cdot\ln(W)$ = $k_{\text{B}}\cdot\ln(1)$ = $0$ $\hspace{.4cm}\text{mit}\hspace{.4cm}\ln(1)=0$

Das bestätigt genau die Aussage des 3. Hauptsatzes der Thermodynamik: Am absoluten Temperaturnullpunkt ( $T=0\,\text{K}$ ) ist die Entropie $S(T=0)=0$ .

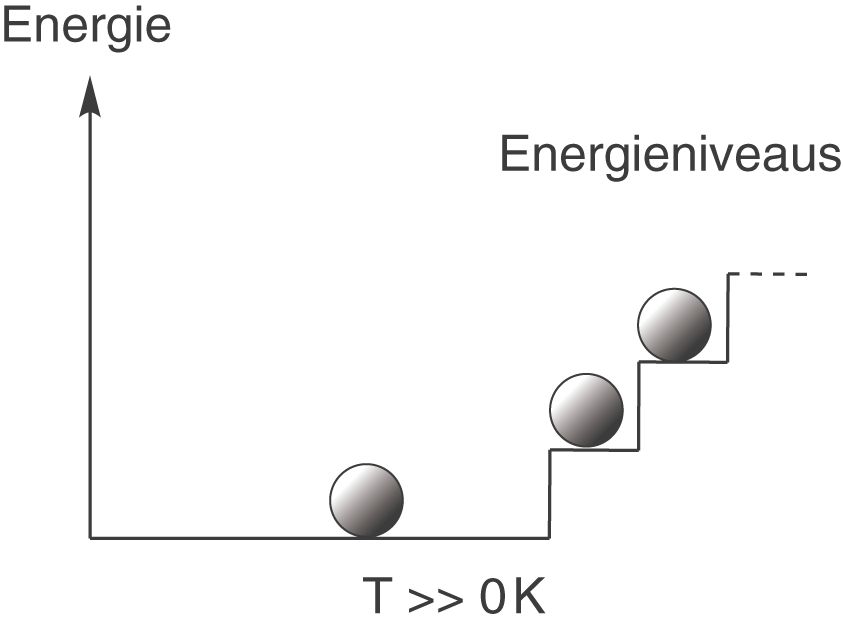
Erhöhen wir nun die Temperatur, dann erhöhen sich auch die Möglichkeiten die verschiedenen Energieniveaus zu besetzen. Diese Verteilung würde dann so aussehen (wie wir oben schon gesehen haben):

Abb. 9: Anregung

Diese Anordnung, also dass genau zwei Atome im Grundzustand anzutreffen sind und eines im ersten angeregten Zustand, stellt den Makrozustand dieses Systems dar. Bei der gegebenen Temperatur, die hier größer null und konstant ist, liegt immer genau diese Anordnung vor. Wenn wir die drei Atome jetzt einfärben, dann könnte das so aussehen:

Abb. 10: Unterschiedliche Anregungen

Der große Unterschied zur farblosen Variante ist jetzt, dass wir nicht mehr nur die Verteilung der Atome bzgl. ihrer Energie im Allgemeinen betrachten (also ihren Makrozustand), sondern, dass wir uns jetzt auch für jedes Atom einzeln interessieren und wissen wollen, wo es sich befindet (Mikrozustände).

Kommen wir hier nochmal auf das erste Beispiel mit $W=1$ zurück. In diesem Fall beschreibt der Makrozustand des Systems die Anordnung, in welcher alle drei Atome im Grundzustand sitzen. Wichtig ist nun, dass wir an dieser Anordnung nichts ändern können, auch nicht dann, wenn wir die Atome einfärben würden und unterscheiden könnten: Sie müssten trotzdem alle im Grundzustand zu finden sein. In diesem Beispiel entspricht der Makrozustand des Systems genau seinem einzigen Mikrozustand.

Zusammenfassend können wir folgendes sagen: Je größer die Entropie des Systems ist, desto mehr Mikrozustände gibt es für einen Makrozustand (wenn du das überprüfen willst, dann überlege dir, wieviele Anordnungsmöglichkeiten du hast, wenn du auch die nächste „Treppenstufe“, also den nächsten angeregten Zustand, mit den eingefärbten Atomen besetzt). Den Begriff der thermodynamischen Wahrscheinlichkeit kannst du so verstehen, dass er die Anzahl der möglichen Mikrozustände des Systems beschreibt. Denn je höher diese Anzahl ist, desto höher ist die Wahrscheinlichkeit der Realisierung des zugehörigen Makrozustands. Jeder Makrozustand besitzt eine unterschiedliche Anzahl an Mikrozuständen, wie wir in den beiden Beispielen oben gesehen haben. Im zweiten Beispiel beträgt die Anzahl der Mikrozustände $W=3$ . Wir hatten also zwei Möglichkeiten mehr, den zugehörigen Makrozustand zu erreichen, wie im Beispiel mit $W=1$ .

Nimmt die Temperatur zu, dann erhöht sich auch die Anzahl der Mikrozustände des jeweiligen Makrozustands und nach der Boltzmann-Gleichung somit auch die Entropie. Das bestätigt auch die Temperaturabhängigkeit der Entropie.

Anmerkung: Das Konzept der Entropie ist wie eingangs bereits erwähnt nicht sehr einfach zu begreifen, da es einerseits sehr abstrakt ist und andererseits zum kompletten Verständnis sehr viel Wissen aus der Chemie und der Physik sowie den Formalismus der Mathematik benötigt, was den Schulstoff sprengen würde. Dennoch konnten wir in diesem Skript bereits eine ganze Menge sehen und die wichtigsten Punkte, die du dir merken solltest, beziehen sich auf den Zusammenhang zwischen Entropie und Unordnung sowie Entropie und die thermodynamische Wahrscheinlichkeit, die Standardentropie und die molare Standardreaktionsentropie und natürlich den Zusammenhang zwischen dem System und damit verbundenen der erlaubten Entropieänderung.

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

Public Domain

[6]

[7]

[8]

[9]

[10]