Elektrolyse

In diesem Skript behandeln wir das Konzept der Elektrolyse. Die Elektrolyse stellt neben dem Galvanischen Element die zweite wichtige Anwendung in der Elektrochemie dar und wird uns insbesondere im Falle von Akkumulatoren interessieren. Bei der Elektrolyse handelt es sich um ein Verfahren, bei welchem durch das Anlegen einer Spannung an Salz- oder Säurelösungen in einer elektrochemischen Zelle chemische Stoffumwandlungen erreicht werden. Diese Tatsahe konnte bereits Michael Faraday, ein englischer Naturforscher und bedeutender Experimentalphysiker des 19. Jahrhunderts, beobachten. Wir wollen die Elektrolyse im Vergleich zu den Galvanischen Elementen betrachten, da wir so schön den Unterschied zwischen beiden Konzepten und Anwendungen herausarbeiten können. Der wichtigste Aspekt liegt darin begründet, dass ein Galvanisches Element in der Lage ist, elektrische Arbeit zu verrichten: Die Redox-Reaktion läuft hier freiwillig ab. Dies ist bei der Elektrolyse nicht der Fall! Bei der Elektrolyse handelt es sich um einen erzwungenen Prozess, bei welchem die Prozesse des Galvanischen Elements durch das Anlegen einer Gleichspannung umgekehrt werden. Wir fassen zusammen:

Galvanisches Element: Prozess läuft freiwillig ab.
Elektrolyse: Prozess ist erzwungen und läuft nicht freiwillig ab.

Wir werden uns nun den Aufbau einer Elektrolysezelle genauer anschauen.

Elektrolysezellen

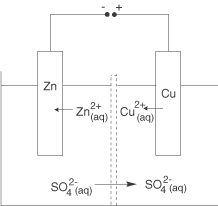
Der experimentelle Aufbau einer Elektrolyse unterscheidet sich vom Galvanischen Element grundlegend dadurch, dass wir die Lampe bzw. das Spannungsmessgerät durch eine Gleichspannungsquelle ersetzen. Wir wollen an dieser Stelle den gleichen Aufbau wie im Falle des Daniell-Elements verwenden, mit eben dieser grundlegenden Änderung.

Abb. 1: Aufbau und Reaktionen in einer galvanischen Zelle

Wir können die hier ablaufenden Reaktion genauso beschreiben, wie alle anderen Redox-Reaktionen auch.

$\text{Zn}^{2+}+2\,\text{e}^{-}$ $\rightleftharpoons$ $\text{Zn}$

$\text{Cu}$ $\rightleftharpoons$ $\text{Cu}^{2+}+2\,\text{e}^{-}$

Der große Unterschied liegt darin begründet, dass die Reaktionen nun genau umgekehrt wie im Falle des Daniell-Elements ablaufen: Zink-Kationen werden reduziert und Kupfer wird oxidiert. Wenn wir an dieser Stelle die Definition für die Anode und die Kathode heranziehen, dann können wir diese bestimmen:

Anode: An der Anode läuft die Oxidation ab $\rightarrow$ die Kupferlelektrode ist hier die Anode.
Kathode: An der Kathode läuft die Reduktion ab $\rightarrow$ die Zinkelektrode ist hier die Kathode.

Wenn wir die beiden Teilreaktionen kombinieren, erhalten wir die Redox-Reaktion:

$\text{Zn}^{2+}+\text{Cu}$ $\rightleftharpoons$ $\text{Cu}^{2+}+\text{Zn}$

Diese entspricht der Rückreaktion der Redox-Reaktion des Daniell-Elements. Ohne das Anlegen einer externen Spannung, also der Bereitstellung von Energie, wird diese Reaktion nicht ablaufen: Es handelt sich um eine erzwungene Redox-Reaktion! Der Ladungsausgleich findet wie bisher auch durch die Wanderung von Sulfat-Anionen statt.

Theorie der Elektrolyse und Elektrodeneffekte

In diesem Kapitel schauen wir uns an, was während der Elektrolyse genau passiert und warum es zur Wanderung der Ionen in Lösung an die Elektroden kommt. Die extern angelegte Spannung führt dazu, dass an einer Elektrode Elektronen entzogen werden, die dann an der anderen Elektrode bereit gestellt werden können. Des Weiteren bildet sich in dem Elektrolyten ein elektrisches Feld aus, welches auf den Einfluss der externen Spannungsquelle zurückzuführen ist. Aus diesem Grund können die Ionen des Elektrolyten auch in der Lösung von einer Elektrode zur anderen wandern und somit den Stromkreis schließen. Wir wollen uns nun mit verschiedenen wichtigen Spannungs- und Potentialbegriffen im Zusammenhang mit der Elektrolyse beschäftigen.

Abscheidungspotential und Überpotential

Wenn wir eine Elektrolyse durchführen wollen, dann wollen wir wissen welche Prozesse an den Elektroden ab wann ablaufen. Das Abscheidungspotential $\boldsymbol{E_{\text{A}}}$ beschreibt den Spannungsbetrag, der notwendig ist, damit ein Stoff an einer Elektrode abgeschieden werden kann. Dieser Betrag entspricht an Platinelektroden dem Redoxpotential $\boldsymbol{E_{\text{h}}}$ des jewiligen Redox-Paares. Das bedeutet, dass für das Redox-Paar $\text{Mg}/\text{Mg}^{2+}$ bei Standardbedingungen beispielsweise ein Abscheidungspotential $\boldsymbol{E_{\text{A}}}$ von $E_{\text{A}}=E_{\text{h}}=-2,36\,\text{V}$ notwendig ist, damit sich elementares Magnesium an der Elektrode abscheidet.
Wenn wir hingegen Graphitelektroden für die Elekrolyse verwenden, dann beobachten wir, dass in dem eben genannten Beispiel bei der aufgeführten Spannung nichts geschieht. Dieses Phänomen liegt im unterschiedlichen Elektrodenmaterial begründet. Die Prozesse, die bei einer Elektrolyse ablaufen, laufen an der Grenzfläche zwischen Elektrode und Elektrolyt ab. Die Eigenschaften der Elektrode haben einen direkten Einfluss auf diese Prozesse, was beispielsweise am Elektrodenmaterial, der Oberflächenbeschaffenheit oder Wechselwirkungen mit dem Reaktanden liegen kann. Diese Effekte werden in Form eines Überpotentials $\boldsymbol{E_{\text{Ü}}}$ zusammengefasst. Für die Abscheidung von Magnesium an einer Graphitelektrode heißt das, dass sich das effektive Abscheidungspotential aus zwei Teilen zusammensetzt:

$E_{\text{A}}$ = $E_{\text{h}}(\text{Mg}/\text{Mg}^{2+})+E_{\text{Ü}}$

Polarisationsspannung, Zersetzungsspannung und Überspannung

Nehmen wir an, wir bringen eine Spannungsquelle an unserem Elektrolyseaufbau an und erhöhen die Spannung kontinuierlich. Was wir beobachten werden, ist folgendes: Bereits bei niedrigen Spannungen werden sich geringe Produktmengen an den Elektroden bilden. Das bedeutet, dass wir hier praktisch lokal ein anderes Elektrodenmaterial erhalten, welches das ursprüngliche überdeckt. Vom Galvanischen Element her wissen wir, dass das Redoxpotential der Redox-Paare an beiden Elektroden auf der Eigenschaft der Lösungstension beruht. Das bedeutet, dass die bereits abgeschiedenen Elemente das Bestreben aufweisen, wieder in Lösung zu gehen: Es bildet sich ein sogenannter Diffusionsstrom aus. Die Spannung, die sich auf der Basis dieser Prozesse zwischen den Elektroden aufbaut, wird Polarisationsspannung genannt. Wir können hierbei beobachten, dass der Strom, der im Fall der Elektrolyse fließt, relativ schwach ist und nur langsam ansteigt.

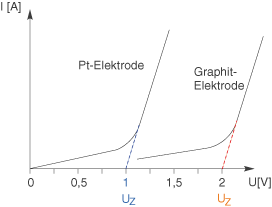
Wenn wir die Spannung bis zu einem gewissen Grad erhöht haben, dann wird die Elektrolyse auf einmal ungehindert ablaufen können. Die Stromstärke, die wir messen können, wird sich nun deutlich erhöhen und linear mit der Spannung ansteigen. Die Spannung, bei der dieser Wechsel eintritt, wird Zersetzungsspannung genannt. Diese entspricht der maximalen Polarisationsspannung. Dazu schauen wir uns den folgenden Graphen an:

Abb. 2: Zersetzungsspannungen verschiedener Elektroden

Links siehst du den Graphen für die Stromstärke-Spannungs-Kurve an einer Platinelektrode. Durch Interpolation der Geraden, dargestellt durch eine gestrichelte Verlängerung dieser, erhalten wir die Zersetzungsspannung dort wo die Gerade die x-Achse schneidet. Rechts siehst du die Stromstärke-Spannungs-Kurve an der Graphitelekrode. Durch die Überspannungseffekte fällt die Zersetzungsspannung deutlich höher aus. Die Zersetzungsspannung $\boldsymbol{U_{\text{Z}}}$ berechnet sich als Differenz der Abscheidungspotentiale:

$$ U_{\text{Z}} = $$ $$ ... $$

Vollständige Formel
anzeigen

Überspannung und Zersetzungsspannung bei Gasen

Ein Problem, das sich hieraus ergibt, ist folgendes: Gase besitzen oft sehr hohen Überspannungen an Elektroden. Das bedeutet, dass die Elektrolyse von Gasen, also beispielsweise die Zersetzung von Säuren und die anschließende elektrolytische Gasproduktion, nur dann effektiv möglich ist, wenn die Überspannung überkompensiert werden kann. Das bedeutet, dass hier oft relativ hohe Zersetzungsspannungen notwendig sind. Bisher scheint das alles noch sehr unproblematisch, bis wir anfangen Wasser als Lösungsmittel zu betrachten. Wir können nämlich auch Wasser durch das Anlegen einer Spannung elektrolysieren. Dieses zersetzt sich dann in elementaren Wasserstoff und Sauerstoff. Wenn die Zersetzungspannung des gewünschten Elektrolyseprodukts größer ist als die von Wasser, dann wird erst das Wasser elektrolysiert werden. Wenn Wasser elektrolysiert wird, dann zersetzt sich einerseits unser Lösungsmittel und andererseits kommt es zur Wasser- und Sauerstoffbildung: Dieses Gemisch ist auch als Knallgas bekannt und hochexplosiv, wenn es energetisch aktiviert wird. Insbesondere im Zusammenhang mit der elektrischen Schaltung kann es hier zur Funkenbildung kommen, wenn die verwendeten Bauteile nicht einwandfrei sind. Dieses Problem kann umgangen werden, indem spezifische Elektroden verwendet werden, die andere Werte für die Überspannung aufweisen, also beispielsweise sehr hohe Überspannungen für die Elektrolyse von Wasser und kleine für das gewünschte Produkt. Durch die Modifikation von Elektroden können diese auf gewünschte Aufgaben zugeschnitten werden.

Die Faraday‘schen Gesetze

Anmerkung: Die Faraday‘schen Gesetze sind nicht zwangsweise im Schulstoff enthalten. Wir werden uns diese Möglichkeit der quantitativen Beschreibung des chemischen Umsatzes an den Elektroden in Verbindung mit den transportierten Ladungen an dieser Stelle anschauen, um ein wenig über den Tellerrand zu schauen. Dieses Kapitel baut auf Grundlagen der Elektrizitätslehre auf, die auch Bestandteil des Schulstoffs sind. Trotzdem, dieses Kapitel ist nicht zwangsweise nötig, um dein Abitur im Fach Chemie erfolgreich zu meistern!

Unsere Betrachtung beruht darauf, dass wir den Stromkreis der Elektrolysezelle in einen äußeren und einen inneren Bestandteil unterteilen können. Der äußere wird durch den Ladungstransport durch Elektronen bestimmt, während der innere durch den Ladungstransport von Ionen in einer wässrigen Elektrolytlösung bestimmt wird. Im äußeren Stromkreis wird im Zeitintervall $\Delta t$ die Ladungsmenge $\Delta Q_{\text{a}}$ transportiert. Dies ist auf den Strom $I$ zurückzuführen:

$\Delta Q_{\text{a}}$ = $I\cdot\Delta t$

Damit der Stromkreis geschlossen ist und kein Ladungsüberschuss entsteht, muss diese Ladungsmenge $\Delta Q_{\text{a}}$ genau der Ladungsmenge entsprechen, die im inneren Stromkreis transportiert wird. Letztere bezeichnen wir mit $\Delta Q_{\text{i}}$ . $\Delta Q_{\text{i}}$ setzt sich folgendermaßen zusammen: An einer Elektrode werden im gleichen Zeitintervall $\Delta t$ $N$ Ionen reduziert oder oxidiert, tauschen also Ladungen aus. Die Ladung der Ionen entspricht einer Zahl $z$ , also beispielsweise $z=2$ für Kupfer(II)-Kationen. Die Menge $N$ der Ionen ist das Produkt der Stoffmenge $n$ dieser Ionen und der Avogadro-Konstante $N_{\text{A}}$ :

$N$ = $n\cdot N_{\text{A}}$

Dieses Produkt liefert uns die Aussage, dass in einem Mol eines Stoffes $6\cdot10^{23}$ Teilchen enthalten sind. Diese Anzahl ist die Größe $N$ . Es handelt sich hierbei also um eine dimensionslose Zahl, welche die Anzahl von Teilchen darstellt. Wenn wir nun einen Schritt weitergehen, dann fällt auf, dass $N$ Zink-Kationen an der Elektrode je zwei Ladungen austauschen können. Das bedeutet, dass hier je $N\cdot2$ Ladungen ausgetauscht werden können. Wenn wir das ganze nun nicht auf Zink-Ionen beschränken wollen, dann können wir auch sagen: Ionen können $z$ Ladungen austauschen. Im Allgemeinen sind das $z\cdot N$ Ladungen oder mit $N=n\cdot N_{\text{A}}$ auch $z\cdot n\cdot N_{\text{A}}$ Ladungen. Wir haben hier also die Anzahl an Ladungen betrachtet, die ausgetauscht werden. Wenn wir nun die Gesamtladung $\Delta Q_{\text{i}}$ bestimmen wollen, dann müssen wir diese dimensionslose Zahl noch mit einer Ladung multiplizieren: Die Ladung stellt die Elementarladung $e$ des Elektrons dar, da diese ausgetauscht werden kann. Damit erhalten wir für $\Delta Q_{\text{i}}$ :

$\Delta Q_{\text{i}}$ = $z\cdot n\cdot N_{\text{A}}\cdot e$

Wenn wir die letzten beiden Größen, also die Avogadro-Konstante $N_{\text{A}}$ und die Elementarladung $e$ zusammenziehen, dann erhalten wir die Ladungsmenge in Coulomb für ein Mol Elektronen. Diese Zahl wird durch die Faradaykonstante $F=96485\,\frac{\text{C}}{\text{mol}}$ verkörpert. Damit ändert sich unsere Gleichung zu:

$\Delta Q_{\text{i}}$ = $z\cdot n\cdot F$

Wir haben ganz am Anfang des Kapitels gesagt, dass die Ladungen des äußeren Stromkreises gleich den Ladungen des inneren Stromkreises sein müssen. Mithilfe der beiden Formeln für $\Delta Q_{\text{a}}$ und $\Delta Q_{\text{i}}$ können wir das auch so schreiben:

$\Delta Q_{\text{a}}$ = $\Delta Q_{\text{i}}$

Mit der Definition der Stoffmenge, als Quotient aus Masse und molarer Masse erhalten wir durch Einsetzen der Formeln:

$I\cdot t$ = $z\cdot \dfrac{m}{M}\cdot F$

Hieraus können wir nun bereits den ersten wichtigen Zusammenhang ablesen, der auch das erste Faraday‘sche Gesetz genannt wird:

$I\cdot t$ \sim $m$

Die Beziehung sagt uns, dass die Masse des an den Elektronen abgeschiedenen Stoffs proportional zur Ladung ist, welche durch die Elektrolysezelle geleitet wird. Bildlich können wir uns das so vorstellen: Je mehr Kationen Elektronen aufnehmen können, desto mehr werden reduziert und folglich erhöht sich auch die Masse des abgeschiedenen Stoffs.

Beispiel: Erstes Faraday‘sches Gesetz

Wir wollen beispielhaft die Elektrolyse von Zink (Zn) betrachten. Dazu wollen wir eine Elektrode in eine Zinksulfat-Lösung ( $\text{ZnSO}_{4\,(\text{aq})}$ ) halten und über einen Zeitraum von $t=60\,\text{min}$ einen Strom von $I=0,5\,\text{A}$ fließen lassen. Dabei wird folgende Reaktion ablaufen:

$\text{Zn}^{2+}+2\,\text{e}^{-}$ $\longrightarrow$ $\text{Zn}$

Hier liegt eine Reduktion vor. Wir wollen nun mit den gegebenen Größen die Masse an Zink berechnen, die in einer Stunde abgeschieden wird.

Gegeben:

Ladungszahl von Zink: $z(\text{Zn})=2$
Dauer: $t=60\,\text{min}=3600\,\text{s}$
Stromstärke: $I=0,5\,\text{A}$
Faraday Konstante: $F=96485\,\frac{\text{C}}{\text{mol}}$
Molare Masse von Zink: $M(\text{Zn})=65,38\,\frac{\text{g}}{\text{mol}}$

Wenn wir diese Größen einsetzen, lautet unsere Gleichung:

$$ m(\text{Zn}) = 0,61\,\text{g} $$ $$ ... $$

Vollständige Formel
anzeigen

In einer Stunde würden wir bei der gegeben Stromstärke Zink mit einer Masse von $m(\text{Zn})=0,61\,\text{g}$ gewinnen.

Das zweite Faraday‘sche Gesetz

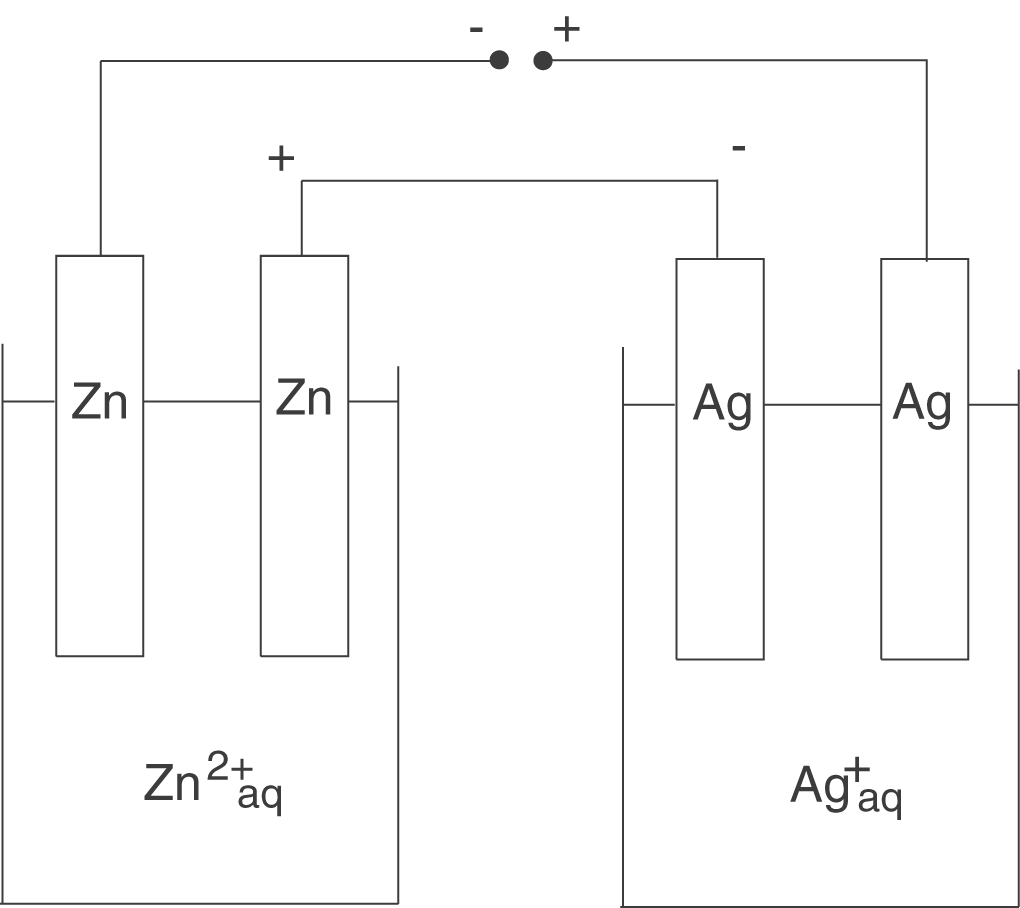
Wir wollen nun eine Elektrolysezelle betrachten, welche neben Zink(II)-Kationen auch Silber-Kationen enthält. Diese könnte folgendermaßen aussehen:

Abb. 3: Elektrolysezelle

In der linken Zelle werden Zink-Kationen reduziert, während in der rechten Zelle Silber-Kationen reduziert werden. Es fließt ein konstanter Strom $I$ über einen Zeitabschnitt $t$ . Wenn wir die Gleichung von oben heranziehen, können wir das so schreiben:

$I\cdot t=z\cdot n\cdot F$ $\hspace{.3cm}\text{mit}\hspace{.3cm}$ $I\cdot t=Q=\text{const.}$

Weiterhin wissen wir, dass dieser Zusammenhang für beide Elemente gelten muss, das heißt:

$Q$ = $z(\text{Ag})\cdot n(\text{Ag})\cdot F$

$Q$ = $z(\text{Zn})\cdot n(\text{Zn})\cdot F$

Zu Beginn dieses Kapitels haben wir gesehen, dass die Ladungen, die im Stromkreis fließen und an den Elektroden ausgetauscht werden konstant sein müssen. Nur so ist der Stromkreis geschlossen. Für dieses Beispiel bedeutet das, dass wir die beiden Formel oben gleichsetzen dürfen.

$z(\text{Zn})\cdot n(\text{Zn})\cdot F$ = $z(\text{Ag})\cdot n(\text{Ag})\cdot F$

Nach ein wenig Umformen erhalten wir spezifisch für unser Beispiel das zweite Faraday‘sche Gesetz:

$\dfrac{n(\text{Zn})}{ n(\text{Ag})}$ = $\dfrac{z(\text{Ag})}{z(\text{Zn})}$ $\hspace{.3cm}\text{mit}\hspace{.3cm}$ $n=\dfrac{m}{M}$

Damit können wir nun beispielsweise die Masse an Silber berechnen, die abgeschieden wird, wenn in der anderen Elektrolysezelle $m(\text{Zn})=1\,\text{g}$ Zink abgeschieden wird. Dazu formen wir nach $m(\text{Ag})$ um.

$n(\text{Ag})$ = $\dfrac{z(\text{Zn})}{z(\text{Ag})}\cdot n(\text{Zn})$

$n(\text{Ag})=\dfrac{z(\text{Zn})}{z(\text{Ag})}\cdot n(\text{Zn})$

Nun setzen wir die Größen ein:

$$ m(\text{Ag}) = 3,3\,\text{g} $$ $$ ... $$

Vollständige Formel
anzeigen

Damit würden wir Silber mit einer Masse von $3,3\,\text{g}$ als Ergebnis erhalten. Mit der gleichen Ladungsmenge können wir hier also ca. das dreifache der Masse von Zink an Silber abscheiden. Noch ein Hinweis zu diesem Ergebnis: Vielleicht wirst du etwas stutzig, wenn du siehst, dass bei gleicher Ladung die dreifache Masse an Silber abgeschieden werden kann, obwohl das Ladungsverhältnis nur 1/2 ist:

$n(\text{Ag})$ = $\dfrac{2}{1}\cdot n(\text{Zn})$

Der Unterschied zwischen dem Stoffmengenverhältnis und dem Massenverhältnis liegt in der molaren Masse der Elemente begründet. Silber ist deutlich schwerer wie Zink, dementsprechend müssen wir Massenverhältnisse und Stoffmengenverhältnisse auch unterscheiden.

Bildnachweise [nach oben]

[1]

[2]

[3]