SchulLV Logo

Puffersysteme

Einführung

Es gibt viele verschiedene Beispiele für natürliche Systeme in denen ein bestimmter pH-Wert so gut es geht konstant gehalten werden muss, damit ein Überleben gesichert wird: der menschliche Blutkreislauf oder natürliche Böden.
Würde sich der pH-Wert in diesen Beispielen sprunghaft ändern, dann würde das einerseits für uns Menschen eine lebensbedrohliche Situtation darstellen, andererseits würde sich die Bodenökologie ändern und die Fruchtbarkeit erheblich in Mitleidenschaft ziehen.
Damit diese Ereignisse nicht auftreten, bedarf es quasi Schutzmechanismen, welche die Systeme gegen starke Schwankungen des pH-Werts schützen. Diese Mechanismen sind in Form von Puffersystemen vorhanden.

Ein Puffersystem ist ein System, welches bei der Zugabe von Säuren und Basen nur mit geringen Schwankungen des pH-Werts reagiert.

Wir wollen uns in diesem Kapitel anschauen, wie diese Puffersysteme aufgebaut sind und wie sie funktionieren.

Quantitative Betrachtung von Puffersystemen

Die Henderson-Hasselbalch-Gleichung


Puffersysteme bestehen aus wässrigen Lösungen, welche eine schwache Säure und ihre korrespondierende Base bzw. eine schwache Base und ihre korrespondierende Säure nebeneinander enthalten. Die Eigenschaften dieses Säure-Base-Paares bestimmt die Funktionsweise und Effektivität der Pufferwirkung.
Wir wollen uns nun anschauen, wie wir die Pufferwirkung quantitativ erfassen können. Dazu betrachten wir ein einfaches Säure-Base-Gleichgewicht der schwachen Säure HA und ihrer korrespondierenden Base \(\text{A}^{-}\).
\(\text{HA}_{(\text{aq})}+\text{H}_{2}\text{O}_{(\ell)}\) \(\rightleftharpoons\) \(\text{A}_{(\text{aq})}^{-}+\text{H}_{3}\text{O}_{(\text{aq})}^{+}\)

(Hierbei könnte es sich beispielsweise um den Essigsäure-Acetat-Puffer handeln)
Für dieses Säure-Base-Gleichgewicht formulieren wir nun im nächsten Schritt das Massenwirkungsgesetz.
\(K_{\text{S}}\) = \(\dfrac{c(\text{A}_{(\text{aq})}^{-})\cdot c(\text{H}_{3}\text{O}_{(\text{aq})}^{+})}{c(\text{HA}_{(\text{aq})})}\)

Aus diesem wollen wir den pH-Wert für unsere Gleichgewichtsreaktion berechnen. Dazu formen wir das Gleichgewicht etwas um.
\(c(\text{H}_{3}\text{O}_{(\text{aq})}^{+})\) = \(K_{\text{S}}\cdot\dfrac{c(\text{HA}_{(\text{aq})})}{c(\text{A}_{(\text{aq})}^{-})}\)

Im Anschluss wenden wir den negativen dekadischen Logarithmus \(-\lg(...)\) auf diese Gleichung an:
\(-\lg(c(\text{H}_{3}\text{O}_{(\text{aq})}^{+}))\) = \(-\lg\left(K_{\text{S}}\cdot\dfrac{c(\text{HA}_{(\text{aq})})}{c(\text{A}_{(\text{aq})}^{-})}\right)\)

Nun verwenden wir die Rechenregeln für Logarithmen:
  • \(\lg(a\cdot b)=\lg(a)+\lg(b)\)
  • \(\lg(\dfrac{a}{b})=-\lg(\dfrac{b}{a})\)
Damit können wir die Gleichung so schreiben:
\(-\lg(c(\text{H}_{3}\text{O}_{(\text{aq})}^{+}))\) = \(-\lg(K_{\text{S}})-\lg\left(\dfrac{c(\text{HA}_{(\text{aq})})}{c(\text{A}_{(\text{aq})}^{-})}\right)\) = \(-\lg(K_{\text{S}})+\lg\left(\dfrac{c(\text{A}_{(\text{aq})}^{-})}{c(\text{HA}_{(\text{aq})})}\right)\)

Mit den Definitionen des pH-Werts und des \(\text{pK}_{\text{S}}\)-Werts
  • \(\text{pH}\) = \(-\lg(c(\text{H}_{3}\text{O}_{(\text{aq})}^{+}))\)
  • \(\text{pK}_{\text{S}}\) = \(-\lg(K_{\text{S}})\)
erhalten wir die Henderson-Hasselbalch-Gleichung:
\(\text{pH}\) = \(\text{pK}_{\text{S}}+\lg\left(\dfrac{c(\text{A}_{(\text{aq})}^{-})}{c(\text{HA}_{(\text{aq})})}\right)\)

Die Pufferwirkung


Um die Pufferwirkung anhand der Henderson-Hasselbalch-Gleichung zu verstehen, betrachten wir im Folgenden ein paar spezielle Fälle, die für das Verhältnis der Konzentrationen des korrespondierenden Säure-Base-Paares auftreten können.

(a) \(c(\text{HA}_{(\text{aq})})=c(\text{A}_{(\text{aq})}^{-})\)


In diesem Fall ist die Konzentration der Säure genauso groß wie die Konzentration der korrespondierenden Base. Wenn wir das in die Henderson-Hasselbalch-Gleichung einsetzen, erhalten wir:
\(\begin{array}{rcl} \text{pH} &=& \text{pK}_{\text{S}} \end{array}\)

Damit erhalten wir für diesen Spezialfall:
\(\text{pH}\) = \(\text{pK}_{\text{S}}\)

Der pH-Wert entspricht also genau dann dem \(\text{pK}_{\text{S}}\)-Wert, wenn das Verhältnis zwischen schwacher Säure und korrespondierender Base äquivalent ist. Dieser Punkt wird Pufferpunkt genannt. Dieser gibt den spezifischen Wirkungsbereich eines Puffersystems wieder.

(b) \(c(\text{HA}_{(\text{aq})})>c(\text{A}_{(\text{aq})}^{-})\)


Diesen Fall erhalten wir, wenn wir Säure zum System zugeben. Beispielhaft wollen wir hier folgende Konzentrationen vorgeben, damit die oben geforderte Bedingung erfüllt ist.
  • \(c(\text{HA}_{(\text{aq})})=10\,c(\text{A}_{(\text{aq})}^{-})\)
Das bedeutet, dass die Konzentration der Säure zehnmal größer ist wie die Konzentration der korrespondierenden Base. Das setzen wir nun wieder in die Henderson-Hasselbalch-Gleichung ein:
\(\begin{array}{rcl} \text{pH} &=& \text{pK}_{\text{S}}-1 \end{array}\)

In diesem Fall wird Base verbraucht und der pH-Wert nimmt um eins ab, obwohl das Verhältnis zwischen Säure und korrespondierender Base 10:1 beträgt. Dieses Verhalten ist auf den dekadischen Logarithmus zurückzuführen. Würde dieser nicht auf das angesprochene Verhältnis angewendet, dann würde der pH-Wert um zehn Einheiten absinken. Dieser Aspekt verdeutlicht die Pufferwirkung unseres Systems.

(c) \(c(\text{HA}_{(\text{aq})})\) < \(c(\text{A}_{(\text{aq})}^{-})\)


Hier sehen wir das Beispiel in dem wir eine Base zu unserem System zugeben. Wir wollen an dieser Stelle das oben gewählte Verhältnis einfach umdrehen:
  • \(c(\text{A}_{(\text{aq})}^{-})=10\,c(\text{HA}_{(\text{aq})})\)
Wir verwenden wieder die Henderson-Hasselbalch-Gleichung und setzen ein:
\(\begin{array}{rcl} \text{pH} &=& \text{pK}_{\text{S}}+1 \end{array}\)

Hier wird Säure verbraucht und der pH-Wert steigt um eine Einheit an. Die Lösung wird im Großen und Ganzen ein wenig basischer, aber dennoch ist die Pufferwirkung sehr effektiv. Ansonsten würde der pH-Wert nämlich um 10 Einheiten ansteigen.
Zusammenfassend können wir sagen, dass das Säure-Base-Paar des Puffersystems zugegebene Säure und Base abpuffert indem es selbst verbraucht wird. Das bedeutet auch gleichzeitig, dass bei Zugabe von zu großen Mengen an Säure bspw. das Puffersystem überlastet werden kann und somit irreparabel geschädigt würde.
Weiterhin ist der \(\text{pK}_{\text{S}}\)-Wert des Puffersystems maßgeblich für den pH-Wert, um den die Pufferwirkung effektiv wirksam ist. Im Fall des oben aufgeführten Beispiels könnten wir sagen, dass der Pufferbereich folgendermaßen um den \(\text{pK}_{\text{S}}\)-Wert schwankt:
\(\text{pH}\) = \(\text{pK}_{\text{S}}\pm1\)

Beispiel: Der Kohlensäure-Carbonat-Puffer

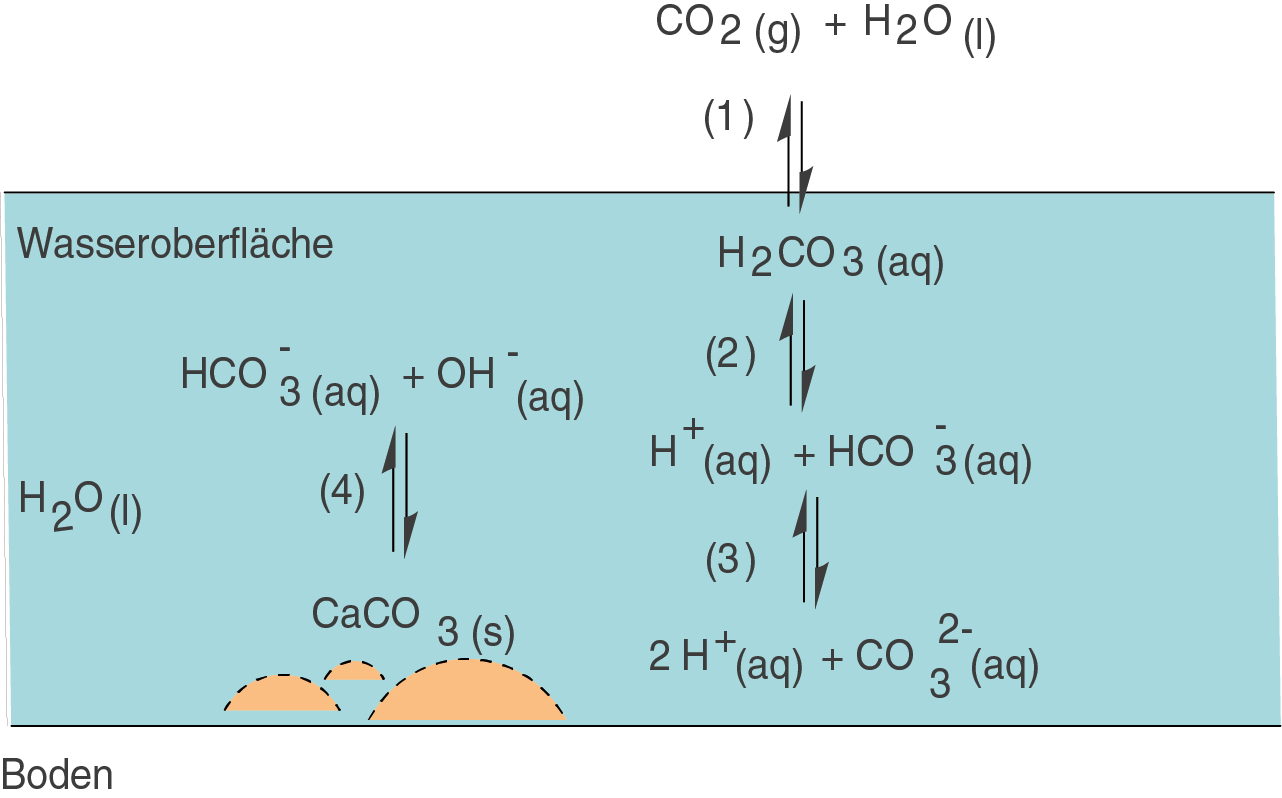
Zum Abschluss des Kapitels wollen wir uns einen der wichtigsten Puffer in der Natur anschauen: den Kohlensäure-Carbonat-Puffer. Die verschiedenen Reaktionspfade sind in der folgenden Graphik dargestellt.


Abb. 1: Kohlensäurereaktion in Wasser

Wir werfen nun einen kurzen Blick auf die einzelnen Reaktionen:

(1): Kohlensäurebildung

Gasförmiges Kohlenstoffdioxid (\(\text{CO}_{2\,(\text{g})}\)) aus der Atmosphäre löst sich in Wasser unter der Bildung der instabilen Kohlensäure (\(\text{H}_{2}\text{CO}_{3\,(\text{aq})}\)).

(2) und (3): Dissoziation der Kohlensäure

Kohlensäure ist eine schwache zweistufige Säure, d.h. sie besitzt zwei Protolysestufen: Die erste (2) ist die Dissoziation in das Hydrogencarbonat-Anion (\(\text{HCO}_{3\,(\text{aq})}^{-}\)) und ein Oxoniumion; die zweite Stufe (3) ist die Dissoziation des Hydrogencarbonat-Anions in das Carbonat-Anion (\(\text{CO}_{3\,(\text{aq})}^{2-}\)) und ein weiteres Oxoniumion.

(4): Lösung von Calciumcarbonat

Festes Calciumcarbonat, auch unter den Namen Calcit oder einfach Kalk bekannt, löst sich in wässrigen Systemen. Es entstehen Hydroxid-Ionen und Hydrogencarbonat-Anionen.

Das gesamte Puffersystem kann dann durch folgende Reaktionsgleichung beschrieben werden:

\(\text{CaCO}_{3\,(\text{s})}+\text{CO}_{2\,(\text{aq})}+\text{H}_{2}\text{O}_{(\ell)}\) \(\rightleftharpoons\) \(\text{Ca}_{(\text{aq})}^{2+}+2\,\text{HCO}_{3\,(\text{aq})}^{-}\)

Du kannst sehen, dass dieser Puffer deutlich komplizierter aufgebaut ist, als beispielsweise der Essigsäure/ Acetat-Puffer. Hierbei hängen viele verschiedene Gleichgewichtssysteme zusammen und neben gelösten Bestandteilen spielen auch die Gasphase \((\text{CO}_{2})\) und die Festphase \((\text{CaCO}_{3})\) eine wichtige Rolle.
Dieser Puffer entfaltet seine Wirkung in einem pH-Bereich zwischen pH 6,2 und 8,6 und schützt natürliche Systeme vor der Versauerung. Wichtig ist zu wissen, dass auch dieser Puffer erschöpft werden kann. Danach üssen andere Prozesse greifen, die die Versauerung aufhalten können, auf welche wir hier aber nicht eingehen.

Bildnachweise [nach oben]
[1]
© SchulLV - 2015