Anwendung: Kalorimeter

Messung von Enthalpieänderungen $\Delta H$

Die chemische Energetik ermöglicht es uns, chemische Reaktionen aus energetischer Sicht zu bewerten. Neben der Richtung der Prozesse ( $\Delta S$ ), spielt auch deren „Triebkraft“ ( $\Delta G$ ) und deren Energieumsatz ( $\Delta H$ ) eine Rolle. Diese drei Größen werden insbesondere auch theoretisch behandelt, um Reaktionen schon vorab charakterisieren zu können. Wenn du dich daran erinnerst, dass du für die Berechnung von $\Delta_{\text{R}}H^{0}$ immer ein Tabellenwerk benötigst, in welchem die Standardbildungsenthalpien $\Delta_{\text{f}}H^{0}$ der jeweiligen Verbindungen gelistet sind, dann können wir uns hier fragen, woher diese Werte kommen.
Wir wollen uns in diesem Skript mit der experimentellen Bestimmung von Enthalpieänderungen $\Delta H$ beschäftigen. Dazu führen wir formal folgendes Experiment durch: Wir verbrennen Magnesium und interessieren uns für den Energiebetrag, der bei dieser chemischen Reaktion umgesetzt wird.

$2\,\text{Mg}_{(\text{s})}+\text{O}_{2\,(\text{g})}$ $\longrightarrow$ $2\,\text{MgO}_{(\text{s})}$ $;\hspace{.3cm}\Delta_{\text{R}}H$ < $0$

Die Verbrennung von Magnesium ist in jedem Fall eine exotherme Reaktion ( $\Delta_{\text{R}}H<0$ ), dass heißt, Energie wird freigesetzt. Diesen Energiebetrag wollen wir nun experimentell bestimmen.

Das Kalorimeter

Um die Messung eines Energieumsatzes zu ermöglichen, benötigen wir ein spezielles Messgerät. Dieses wird Kalorimeter genannt, von griech. calor „Wärme“. Wir schauen uns in den nächsten beiden Kapiteln den Aufbau eines solchen Kalorimeters an und stellen Überlegungen zur Durchführung des Versuchs an. Im Anschluss werden wir uns dann mit dem Ergebnis beschäftigen und die Auswertung durchführen.

Aufbau und Durchführung

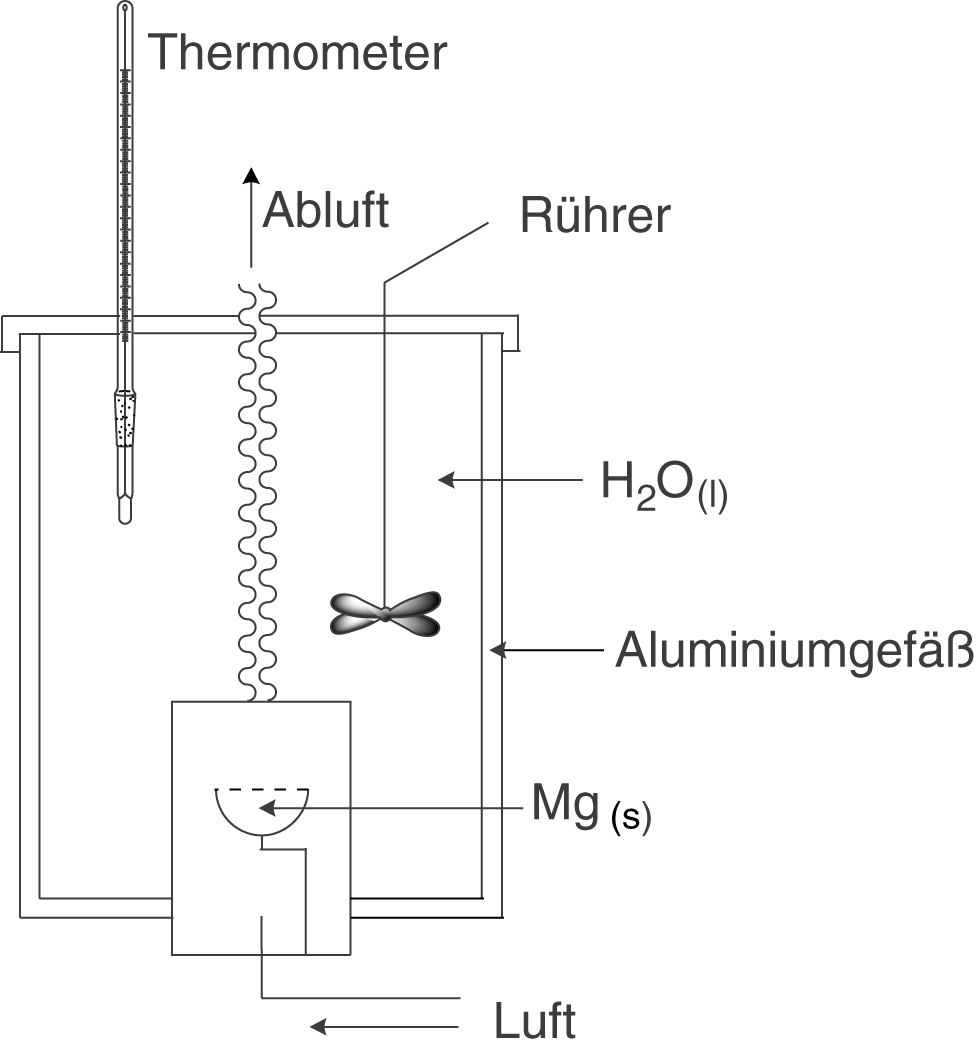
Zunächst werfen wir einen Blick auf den Aufbau des Kalorimeters:

Thermometer: Temperaturmessung
Rührer: gleichmäßige Vermischung; relativ homogene Wärmeverteilung wird gewährleistet.
Luftzufuhr: $\text{O}_{2\,(\text{g})}$ ist für die Verbrennung notwendig.
$\text{Mg}_{(\text{s})}$ : befindet sich in einem kleinen Behälter und wird verbrannt.
Wasser dient als Medium, welches die abgegebene Wärme aufnehmen soll.
Das Kalorimeter ist ein Gefäß aus Aluminium.

Diagramm eines chemischen Experiments mit Thermometern, Abluft und Rührer in einem Aluminiumgefäß.

Abb. 1: Aufbau eines Kalorimeters

Das Kalorimeter ist ein geschlossenes Gefäß, dessen Masse $m_{\text{Kal}}$ wir genau kennen. Weiterhin ist es komplett mit einer bekannten Masse an Wasser $m_{\text{Wasser}}$ gefüllt . Im Inneren befindet sich eine Reaktionskammer, in welcher das Magnesium in unserem Fall verbrannt werden wird. Da hierzu Sauerstoff notwendig ist, benötigen wir eine Luftzufuhr sowie eine Möglichkeit der Abluftabfuhr. Ein Rührer führt dazu, dass das Wasser im Kalorimeter immer gut durchmischt wird und sich die Wärme relativ gleichmäßig verteilen kann. Die Wärmeänderung $\Delta T$ können wir mit einem gewöhnlichen Thermometer messen.

2. Durchführung

Wir bringen das Magnesium und den Sauerstoff zur Reaktion, indem wir eine Aktivierungsenergie $E_{\text{A}}$ zuführen. Das Magnesium wird verbrennen und ein gewisser Betrag an Reaktionsenthalpie $\Delta_{\text{R}}H$ wird in Form von Wärmeenergie $\Delta Q$ frei. Diese Wärmeenergie wird sowohl an das Wasser, als auch an das Kalorimeter abgegeben. Dieser Aspekt ist insbesondere bei der Auswertung und Berechnung später sehr wichtig. Mithilfe des Thermometers können wir die Temperaturänderung $\Delta T$ des Wassers messen. Wir führen diesen Versuch bei Standardbedingungen durch.

Auswertung und Berechnung

Wir wollen unsere Beobachtungen nun auswerten und die Standardreaktionsenthalpie $\Delta_{\text{R}}H$ von Magnesium berechnen. Zunächst betrachten wir das System, in welchem die Verbrennung stattfindet. Da die Reaktionskammer eine Öffnung in Form der Abluftabfuhr besitzt, führen wir das Experiment unter Atmosphärendruck durch. Damit ist der Druck $p=\text{const.}$ . Diese Tatsache macht es möglich, dass wir den Zusammenhang zwischen der Reaktionsenthalpie $\Delta_{\text{R}}H$ und der Wärmeenergie $\Delta Q$ herstellen können (vgl. das ChemieLV-Skript Die Enthalpie):

$\text{Für}\hspace{.2cm}p=\text{const.}:$ $\hspace{.2cm}\Delta Q=\Delta Q_{\text{p}}$ $;\hspace{.4cm}\Delta Q_{\text{p}}=\Delta_{\text{R}}H$

Nun stellen wir ein paar Überlegungen zur Wärmeenergie $\Delta Q$ an. Wenn das Magnesium verbrennt, dann wird sich neben dem Wasser auch das Kalorimeter an sich erwärmen. Das heißt, dass sich die Gesamtwärmemenge letztendlich in zwei Teilwärmemengen aufteilen lässt: Die Wärmeenergie, die durch das Wasser aufgenommen wird $\Delta Q_{\text{Wasser}}$ und die Wärmeenergie, die durch das Kalorimeter aufgenommen wird $\Delta Q_{\text{Kal}}$ . Damit können wir die Änderung der Gesamtwärmeenergie $\Delta Q_{\text{gesamt}}$ als Summe der beiden Teiländerungen schreiben:

$\Delta Q_{\text{gesamt}}=\Delta Q_{\text{Wasser}}+\Delta Q_{\text{Kal}}$

Diese Gesamtänderung der Wärmeenergie $\Delta Q_{\text{gesamt}}$ entspricht dem $\Delta Q_{\text{p}}$ von oben.

Die nächste Frage, die wir uns stellen müssen, bezieht sich darauf, wie die beiden Teiländerungen $\Delta Q_{\text{Wasser}}$ und $\Delta Q_{\text{Kal}}$ zustande kommen und von was sie abhängen. Prinzipiell können wir uns vorstellen, dass wir für ein sehr großes Kalorimeter sehr viel mehr Wärmeenergie aufwenden müssen, um eine bestimmte Temperaturänderung $\Delta T$ herbeizuführen, als bei einem kleinen Kalorimeter, um die gleiche Temperaturänderung zu erhalten: Die Masse $m$ des betrachteten Objekts spielt demnach eine Rolle. Je schwerer das betrachtete Objekt ist, desto mehr Wärmeenergie wird benötigt, um die gleiche Temperaturänderung $\Delta T$ herbeizuführen. Für uns sind folglich die Masse des Wassers $m_{\text{Wasser}}$ und die Masse des Kalorimeters $m_{\text{Kal}}$ von Bedeutung.

Die zweite Größe, die uns interessiert, bezieht sich auf die Fähigkeit eines bestimmten Stoffes Wärmeenergie aufzunehmen. Manche Stoffe sind in der Lage sehr viel Wärmeenergie aufzunehmen, bei relativ geringer Temperaturänderung. Andere verhalten sich genau gegenteilig. Diese Eigenschaft wird durch die GrÖße der Wärmekapazität $\boldsymbol{c}$ verkörpert. In unserem Fall ist auch hier wieder die Wärmekapazität des Kalorimeters $c_{\text{Kal}}$ , als auch die Wärmekapazität des Wassers $c_{\text{Wasser}}$ von Interesse. Die Wärmekapazität eines Stoffes gibt dir darüber Auskunft, welche Energiemenge in Joule du aufwenden musst, um die Temperatur von einem Gramm eines Stoffes, um ein Kelvin zu erhöhen.

An dritter Stelle steht die Temperaturänderung $\Delta T$ . Diese Temperaturänderung stellt die Differenz zwischen der Endtemperatur $T_{\text{end}}$ , nach der Reaktion, und der Anfangstemperatur $T_{0}$ , zu Beginn der Reaktion, dar.
Das Erarbeitete können wir nun in Form von Formeln notieren:

$\Delta Q_{\text{Wasser}}$ = $c_{\text{Wasser}}\cdot m_{\text{Wasser}}\cdot\Delta T$

$\Delta Q_{\text{Kal}}$ = $c_{\text{Kal}}\cdot m_{\text{Kal}}\cdot\Delta T$

Im nächsten Schritt verwenden wir diese beiden Formeln und setzen sie in die Definition für $\Delta Q_{\text{gesamt}}$ ein:

$\Delta Q_{\text{gesamt}}$ = $\Delta Q_{\text{Wasser}}+\Delta Q_{\text{Kal}}$ = $c_{\text{Wasser}}\cdot m_{\text{Wasser}}\cdot\Delta T+c_{\text{Kal}}\cdot m_{\text{Kal}}\cdot\Delta T$

Zur Vereinfachung können wir im letzten Schritt noch $\Delta T$ ausklammern:

$\Delta Q_{\text{gesamt}}$ = $(c_{\text{Wasser}}\cdot m_{\text{Wasser}}+c_{\text{Kal}}\cdot m_{\text{Kal}})\cdot\Delta T$

Mit dieser Formel können wir die Reaktionsenthalpie $\Delta_{\text{R}}H$ berechnen: $\Delta_{\text{R}}H=\Delta Q_{\text{gesamt}}$ .

Wir gehen nun daran unser Experiment auszuwerten: Die Verbrennung von Magnesium in einem Aluminiumkalorimeter. Folgende Größen sind gegeben:

$m_{\text{Magnesium}} = 1\,\text{g}$
$m_{\text{Wasser}}=400\,\text{g}$
$m_{\text{Kal}}=200\,\text{g}$
$c_{\text{Wasser}}=4,182\,\frac{\text{J}}{\text{g}\cdot\text{K}}$
$c_{\text{Kal}}=0,896\,\frac{\text{J}}{\text{g}\cdot\text{K}}$
$\Delta T=13,35\,\text{K}$

Durch Einsetzen der gegebenen Größen berechnen wir die Reaktionsenthalpie. Beachte, dass wir hier eine Größe berechnen, die ein positives Vorzeichen haben wird. Das ist dadurch möglich, dass wir in diesem Fall den Betrag der Reaktionsenthalpie berechnen. Wir bekommen auf diesem Weg prinzipiell keine Aussage darüber, ob diese Reaktion exotherm oder endotherm verläuft.

$\begin{array}{rcl} \Delta Q_{\text{gesamt}}&=& 24,7\,\text{kJ} \end{array}$

Vollständige Lösung anzeigen

Da dieser Wert auf ein Gramm bezogen ist, können wir ihn noch auf die Stoffmenge in mol umrechnen:

$\Delta_{\text{R}}H$ = $\Delta Q_{\text{gesamt}}\cdot M(\text{Mg})$ = $24,7\,\frac{\text{kJ}}{\text{g}}\cdot24,31\,\frac{\text{g}}{\text{mol}}$ = $600,57\,\frac{\text{kJ}}{\text{mol}}$

Bei der Verbrennung von einem Mol Magnesium werden nach unserer Berechnung $600,57\,\text{kJ}$ frei. Dieses Ergebnis ist sehr nahe am Literaturwert von $\Delta_{\text{R}}H=-601\,\dfrac{\text{kJ}}{\text{mol}}$ .

Berechnung unbekannter Wärmekapazitäten

Eine weitere wichtige Anwendung des Kalorimeters besteht darin, die Wärmekapazitäten von Materialien zu bestimmen. Es wird eine Reaktion mit bekannter Standardreaktionsenthalpie gewählt, die in einem Kalorimeter abläuft, dessen Wärmekapazität unbekannt ist. Durch Auflösen der Formel nach der gesuchten Variable, kannst du diese unbekannte Wärmekapazität berechnen. Das Umstellen dieser Formel ist etwas trickreicher, weswegen wir hier ausführlich vorgehen wollen:

$(1)\hspace{.3cm}\Delta Q_{\text{gesamt}}$ = $c_{\text{Wasser}}\cdot m_{\text{Wasser}}+c_{\text{Kal}}\cdot m_{\text{Kal}})\cdot\Delta T$

Wir teilen durch $\Delta T$ :

$(2)\hspace{.3cm}\dfrac{\Delta Q_{\text{gesamt}}}{\Delta T}$ = $c_{\text{Wasser}}\cdot m_{\text{Wasser}}+c_{\text{Kal}}\cdot m_{\text{Kal}}$

Anschließend bringen wir den Term $c_{\text{Wasser}}\cdot m_{\text{Wasser}}$ auf die andere Seite:

$(3)\hspace{.3cm}\dfrac{\Delta Q_{\text{gesamt}}}{\Delta T}-c_{\text{Wasser}}\cdot m_{\text{Wasser}}$ = $c_{\text{Kal}}\cdot m_{\text{Kal}}$

Zum Abschluss teilen wir durch $m_{\text{Kal}}$ :

$(4)\hspace{.3cm}(\dfrac{\Delta Q_{\text{gesamt}}}{\Delta T}-c_{\text{Wasser}}\cdot m_{\text{Wasser}})\cdot\dfrac{1}{m_{\text{Kal}}}$ = $c_{\text{Kal}}$

Wenn wir diese Formel nun noch umdrehen, dann erhalten wir:

$c_{\text{Kal}}$ = $(\dfrac{\Delta Q_{\text{gesamt}}}{\Delta T}-c_{\text{Wasser}}\cdot m_{\text{Wasser}})\cdot\dfrac{1}{m_{\text{Kal}}}$

So können wir eine unbekannte Wärmekapazität des Kalorimetermaterials $c_{\text{Kal}}$ berechnen. Wenn wir den rechten Term in der Klammer um $\Delta T$ erweitern, auf einen Bruchstrich schreiben und die Klammer mit dem Faktor $\dfrac{1}{m_{\text{Kal}}}$ multiplizieren erhalten wir:

$c_{\text{Kal}}$ = $\dfrac{\Delta Q_{\text{gesamt}}-\Delta Q_{\text{Wasser}}}{\Delta T\cdot m_{\text{Kal}}}$

Diese Darstellung ist prinzipiell einfacher. Problematisch ist nur, dass wir oft nicht direkt wissen, welche Wärmemenge das Wasser ( $\Delta Q_{\text{Wasser}}$ ) aufgenommen hat. Diese müssen wir somit berechnen und deshalb ist die erste Variante wohl oft zweckmäßiger.

Bildnachweise [nach oben]

[1]

Public Domain