Massenwirkungsgesetz

Theorie des Massenwirkungsgesetzes (MWG)

Einführung

Das Massenwirkungsgesetz ist die mathematische Formulierung chemischer Gleichgewichtsreaktionen. Wir werden uns in diesem Kapitel anschauen, wie das Massenwirkungsgesetz aufgestellt wird, was insbesondere die Gleichgewichtskonstante $K$ für eine Rolle spielt und was wir dem Massenwirkungsgesetz für Informationen über die Lage des Gleichgewichts entnehmen künnen.

Herleitung des Massenwirkungsgesetzes

Wichtig:

Im Folgenden wollen wir kurz darauf eingehen, aus welchen Gesetzmäßigkeiten und Annahmen das Massenwirkungsgesetz hergeleitet werden kann. Dies übersteigt den Abitursstoff ein wenig, deshalb kannst du direkt zum nächsten Kapitel springen, wenn du hieran kein Interesse haben solltest.

Wie in der Einleitung bereits erwähnt, ist ein chemisches Gleichgewicht dadurch charakterisiert, dass sich die Konzentrationen der Reaktanden in diesem Zustand nicht mehr ändern. Weiterhin läuft jedoch trotzdem eine Hinreaktion und eine Rückreaktion ab. Da dies aber gleich schnell geschieht, ändert sich makroskopisch quasi nichts mehr. Mikroskopisch läuft die Reaktion hingegen weiter ab. Aus diesem Grund spricht man hierbei auch von einem dynamischen Gleichgewicht. Wir wollen an dieser Stelle beispielhaft folgendes Gleichgewicht betrachten:

$a\cdot\text{A}+b\cdot\text{B}$ $\rightleftharpoons$ $c\cdot\text{C}+d\cdot\text{D}$

Dabei sind A, B, C und D jeweils die Reaktanden der Reaktion und $a$ , $b$ , $c$ und $d$ die stöchiometrischen Koeffizienten.
Hin- und Rückreaktion sind nun beide durch je eine Reaktionsgeschwindigkeit charakterisiert, die wir $v_{\text{Hin}}$ und $v_{\text{Rück}}$ nennen wollen und für die gilt:

$v_{\text{Hin}}$ = $k_{\text{Hin}}\cdot c(\text{A})^{a}\cdot c(\text{B})^{b}$

$v_{\text{Rück}}$ = $k_{\text{Rück}}\cdot c(\text{C})^{c}\cdot c(\text{D})^{d}$

$k_{\text{Hin}}$ und $k_{\text{Rück}}$ sind dabei zwei Konstanten, die als Geschwindigkeitskoeffizienten bezeichnet werden und spezifisch für jede Reaktion sind. Weiterhin kannst du hier sehen, dass die stöchiometrischen Koeffizienten, die Vorfaktoren $a$ , $b$ , $c$ und $d$ in diesem Zusammenhang bereits als Exponenten der Konzentrationen ihrer jeweiligen Reaktanden auftreten, wie auch im Massenwirkungsgesetz.

Für ein System im dynamischen Gleichgewicht gilt nun weiterhin:

$v_{\text{Hin}} = v_{\text{Rück}}$

Davon sind wir am Anfang ausgegangen: die Geschwindigkeiten der Hin- und Rückreaktion sind beide gleich groß. Graphisch können wir das anhand von diesen Graphen darstellen:

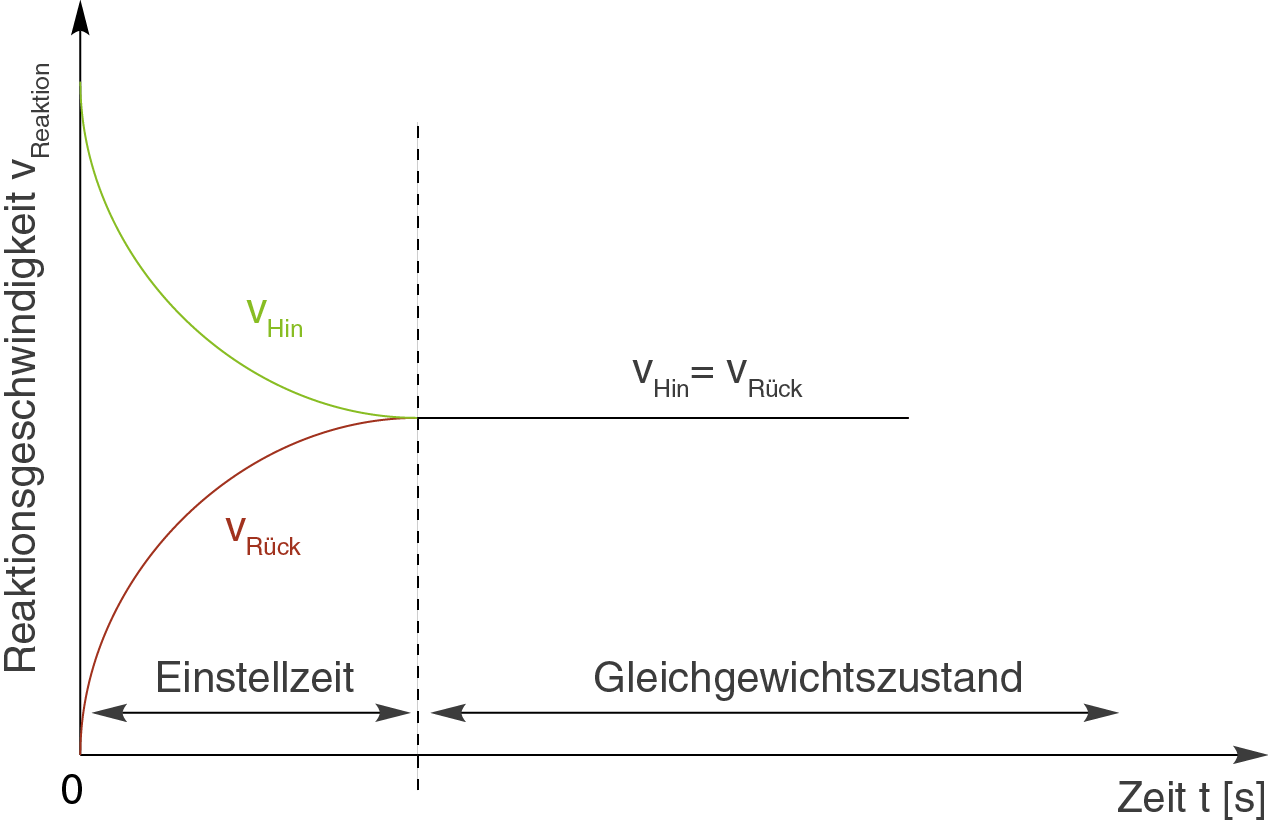
Diagramm zur Reaktionsgeschwindigkeit über die Zeit mit Einstellzeit und Gleichgewichtszustand.

Abb. 1: Konzentrationsverläufe

Wir können für die Reaktionsgeschwindigkeiten $v_{\text{Hin}}$ und $v_{\text{Rück}}$ beide Ausdrücke von oben in diese Gleichung einsetzen:

$k_{\text{Hin}}\cdot c(\text{A})^{a}\cdot c(\text{B})^{b}$ = $k_{\text{Rück}}\cdot c(\text{C})^{c}\cdot c(\text{D})^{d}$

Anschließend bringen wir noch die beiden Geschwindigkeitskoeffizienten $k_{\text{Hin}}$ und $k_{\text{Rück}}$ auf eine Seite und die Produkte der Konzentrationen der Reaktanden auf die andere.

$\dfrac{k_{\text{Hin}}}{k_{\text{Rück}}}$ = $\dfrac{c(\text{C})^{c}\cdot c(\text{D})^{d}}{c(\text{A})^{a}\cdot c(\text{B})^{b}}$

Da beide Geschwindigkeitskoeffizienten konstant sind, können wir im letzten Schritt den Quotienten aus $k_{\text{Hin}}$ und $k_{\text{Rück}}$ zu einer eine Konstante zusammenfassen, nämlich die Gleichgewichtskonstante $K$ .
Somit gilt:

$K$ = $\dfrac{k_{\text{Hin}}}{k_{\text{Rück}}}$ = $\dfrac{c(\text{C})^{c}\cdot c(\text{D})^{d}}{c(\text{A})^{a}\cdot c(\text{B})^{b}}$

Das Massenwirkungsgesetz (MWG)

Das Massenwirkungsgesetz

$K$ = $\dfrac{c(\text{C})^{c}\cdot c(\text{D})^{d}}{c(\text{A})^{a}\cdot c(\text{B})^{b}}$

gilt ganz allgemein für die Gleichgewichtsreaktion

$a\cdot\text{A}+b\cdot\text{B}$ $\rightleftharpoons$ $c\cdot\text{C}+d\cdot\text{D}$

Ein wichtiger Punkt, den wir gleich von Beginn an ansprechen wollen, sind die Exponenten der jeweiligen Konzentrationen im MWG. Die stöchiometrischen Koeffizienten der Reaktanden treten im MWG als Exponenten der jeweiligen Konzentrationen auf. Das bedeutet, dass die Stöchiometrie der Gleichgewichtsreaktion einen erheblichen Einfluss auf die Gleichgewichtskonstante $K$ und somit auf die Lage des chemischen Gleichgewichts hat.

Informationsgehalt des MWG

Nachdem wir nun wissen, wie das Massenwirkungsgesetz formell aufgebaut ist, wollen wir uns im nächsten Schritt darum kümmern seinen Informationsgehalt zu ergründen. So wirst du lernen, dieses Wissen auf diverse Gleichgewichtssysteme anzuwenden und die Informationen, die dir das Massenwirkungsgesetz liefert, richtig zu interpretieren.
Wir gehen dabei so vor, dass wir uns die beiden Seiten der Gleichung näher anschauen und dann anhand von Beispielen genauer untersuchen, wie sich das MWG verhält. Wir wollen uns anschauen, was wir an den beiden Seiten der Gleichung ändern können, d.h. wir spielen in gewisser Weise an dieser Stelle mit den Größen im MWG, um zu sehen was passieren wird.
Was du im MWG siehst, ist der Quotient aus dem Produkt der Konzentrationen der Produkte und dem Produkt der Konzentrationen der Edukte.

Drei rechnerische Fälle können wir für das MWG unterscheiden:

1. Zähler gleich groß wie Nenner
Wir setzen:

$c(\text{C})^{c}\cdot c(\text{D})^{d}$ = $c(\text{A})^{a}\cdot c(\text{B})^{b}$

Das heißt, die Produkte der jeweiligen Konzentrationen sind identisch, wir bekommen

$K$ = $\dfrac{c(\text{C})^{c}\cdot c(\text{D})^{d}}{c(\text{A})^{a}\cdot c(\text{B})^{b}}$ = $1$

Sobald Nenner und Zähler gleich sind, ist die Gleichgewichtskonstante gleich 1.

2. Zähler größer als Nenner
Wir setzen:

$c(\text{C})^{c}\cdot c(\text{D})^{d}$ > $c(\text{A})^{a}\cdot c(\text{B})^{b}$

Als MWG formuliert heißt das:

$K$ = $\dfrac{c(\text{C})^{c}\cdot c(\text{D})^{d}}{c(\text{A})^{a}\cdot c(\text{B})^{b}}$ > $1$

Wenn das Produkt der Konzentrationen der Produkte größer ist als das Produkt der Konzentrationen der Edukte ist der Zähler größer als der Nenner.

3. Zähler kleiner als Nenner
Wir setzen:

$c(\text{C})^{c}\cdot c(\text{D})^{d}$ < $c(\text{A})^{a}\cdot c(\text{B})^{b}$

Und wenden auch diese Annahme auf das MWG an:

$K$ = $\dfrac{c(\text{C})^{c}\cdot c(\text{D})^{d}}{c(\text{A})^{a}\cdot c(\text{B})^{b}}$ < $1$

Der dritte Fall ist genau das Gegenteil vom zweiten Fall. Als Ergebnis erhalten wir eine Gleichgewichtskonstante, die kleiner als 1 ist. Dies beruht darauf, dass die Konzentrationen der Edukte diesmal größer ist als das Produkt der Konzentrationen der Produkte.
$K$ kann größer, kleiner oder gleich eins sein, aber nie null oder negative Werte annehmen.
Nach dieser theoretischen und sehr allgemeinen Betrachtung, gehen wir jetzt dazu über, das Erarbeitete auf ein konkretes Gleichgewichtssystem anzuwenden und zu schauen, was uns die Größe $K$ für Informationen bzgl. des Gleichgewichts liefern kann.

Das Massenwirkungsgesetz in der Praxis

In diesem Kapitel wirst du nun verstehen lernen, was die Gleichgewichtskonstante $K$ aussagt, insbesondere im Bezug auf die drei Fälle, die du gerade kennen gelernt hast. Die wichtigste Information, die dir die Gleichgewichtskonstante liefert, ist die Lage des chemischen Gleichgewichts.
Die Aussage der Gleichgewichtskonstanten werden wir nun an drei beispielhaften Gleichgewichtslagen der folgenden Gleichgewichtsreaktion erörtern:

$\text{H}_{2\,(\text{g})}+\text{I}_{2\,(\text{g})}$ $\rightleftharpoons$ $2\;\text{HI}_{(\text{g})}$

K > 1: Gleichgewicht auf der Produktseite

Liegt das Gleichgewicht auf der Seite der Produkte, dann bedeutet das, dass die Konzentration der Produkte größer ist als die der Edukte. Da wir in diesem Fall ein bestimmtes chemisches Gleichgewicht betrachten, können wir sagen, dass die Konzentration an Iodwasserstoff $c(\text{HI}_{\text{(g)}})$ größer ist als die Konzentrationen der Edukte Wasserstoff und Iod.
Dieses Wissen wenden wir jetzt auf das Massenwirkungsgesetz an:

$K$ = $\dfrac{c^{2}(\text{HI}_{\text{(g)}})}{c(\text{H}_{2\,\text{(g)}})\cdot c(\text{I}_{2\,\text{(g)}})}\gt 1$ mit $c^{2}(\text{HI}_{\text{(g)}})\gt c(\text{H}_{2\,\text{(g)}})\cdot c(\text{I}_{2\,\text{(g)}})$

Um die Lage dieses Gleichgewichts bzw. eines allgemeinen Gleichgewichts bestimmten zu können, benötigen wir demnach die Konzentrationen der Reaktanden im Gleichgewichtszustand.

K < 1: Gleichgewicht auf der Eduktseite

Ist hingegen die Konzentration der Edukte größer als die der Produkte, dann liegt das Gleichgewicht auf der Seite der Edukte. Konkret bedeutet dies, dass die Reaktion nicht sehr effektiv abläuft, da die Edukte nicht in großer Menge zu dem eventuell gewünschten Produkt umgesetzt werden.

$K=\dfrac{c^{2}(\text{HI}_{\text{(g)}})}{c(\text{H}_{2\,\text{(g)}})\cdot c(\text{I}_{2\,\text{(g)}})}\lt 1$ mit $c^{2}(\text{HI}_{\text{(g)}})\lt c(\text{H}_{2\,\text{(g)}})\cdot c(\text{I}_{2\,\text{(g)}})$

K = 1: Gleichgewicht in der Mitte

Als dritten Fall wollen wir noch die Gleichheit der Edukt- und Produktkonzentrationen behandeln.

$K=\dfrac{c^{2}(\text{HI}_{\text{(g)}})}{c(\text{H}_{2\,\text{(g)}})\cdot c(\text{I}_{2\,\text{(g)}})}=1$ mit $c^{2}(\text{HI}_{\text{(g)}})=c(\text{H}_{2\,\text{(g)}})\cdot c(\text{I}_{2\,\text{(g)}})$

Einheitenbetrachtung

Zum Abschluss dieses Kapitels werden wir noch die Einheit der Gleichgewichtskonstanten $K$ ansprechen.
Wir betrachten:

$[K]$ = $\dfrac{\left[c(\text{HI}_{\text{(g)}})\right]^2}{\left[c(\text{H}_{2\,\text{(g)}})\right]\cdot \left[c(\text{I}_{2\,\text{(g)}})\right]}$ = $\dfrac{(\text{mol}\cdot \text{L}^{-1})^{2}}{\text{mol}\cdot \text{L}^{-1}\cdot\text{mol}\cdot \text{L}^{-1}}$ = $1$

Die eckigen Klammern sind eine Notation dafür, dass wir uns für die Einheiten der betrachteten Gößen interessieren. Du siehst, dass sich für das Beispiel der Gleichgewichtsreakion von Iod und Wasserstoff zu Iodwasserstoff die Einheiten gerade herauskürzen, so dass die Gleichgewichtskonstante $K$ in diesem Fall letztendlich keine Einheit hat. Jedoch kann es auch vorkommen, dass das MWG einer Reaktion als Einheit z.B. mol $\cdot$ L $^{-1}$ , mol $^2$ $\cdot$ L $^{-2}$ , etc. aufweist. Die Einheit der Gleichgewichtskonstante $\boldsymbol{K}$ hängt von der Anzahl der Reaktanden ab, deren Konzentration als Faktoren ins MWG miteinfließen. Somit hat die Gleichgewichtskonstante $K$ keine feste Einheit; sie ist immer abhängig von der jeweiligen Reaktion.
Bedenke an dieser Stelle, dass $\ell^{-2}$ = $\dfrac{1}{\ell^{2}}$ .

Verschiedene Gleichgewichtszustände

Am Ende dieses Kapitels kannst du die Frage stellen, wie es uns möglich war, drei unterschiedliche Gleichgewichtsituationen für eine einzige Gleichgewichtsreaktion zu betrachten. Wir werden uns aus diesem Grund im nächsten Kapitel mit der Beeinflussung von chemischen Gleichgewichten und damit verbunden mit dem Prinzip vom kleinsten Zwangs nach Le Chatelier beschäftigen. Damit wirst du in der Lage sein, chemische Gleichgewichte nach deinen Vorstellungen zu beeinflussen, was von großem Nutzen sein kann, wie du spätestens im Kapitel Anwendungen sehen wirst.

Bildnachweise [nach oben]

[1]