Teil A
1
Gegeben ist die Funktion  durch
durch 

a)
Skizziere den Graphen von 
(1 BE)
b)
Der Graph von  begrenzt mit der
begrenzt mit der  -Achse eine Fläche vollständig.
-Achse eine Fläche vollständig.
Berechne den Flächeninhalt dieser Fläche.
Berechne den Flächeninhalt dieser Fläche.
(2 BE)
c)
Der Graph der Funktion  geht durch Streckung in
geht durch Streckung in  -Richtung aus dem Graphen von
-Richtung aus dem Graphen von  hervor.
hervor.
Der Graph von schließt mit der
schließt mit der  -Achse eine Fläche von
-Achse eine Fläche von  ein.
ein.
Bestimme eine zugehörige Funktionsgleichung für
Der Graph von
Bestimme eine zugehörige Funktionsgleichung für
(2 BE)
2
Der Graph einer ganzrationalen Funktion  dritten Grades besitzt an der Stelle
dritten Grades besitzt an der Stelle  einen Tiefpunkt.
einen Tiefpunkt.
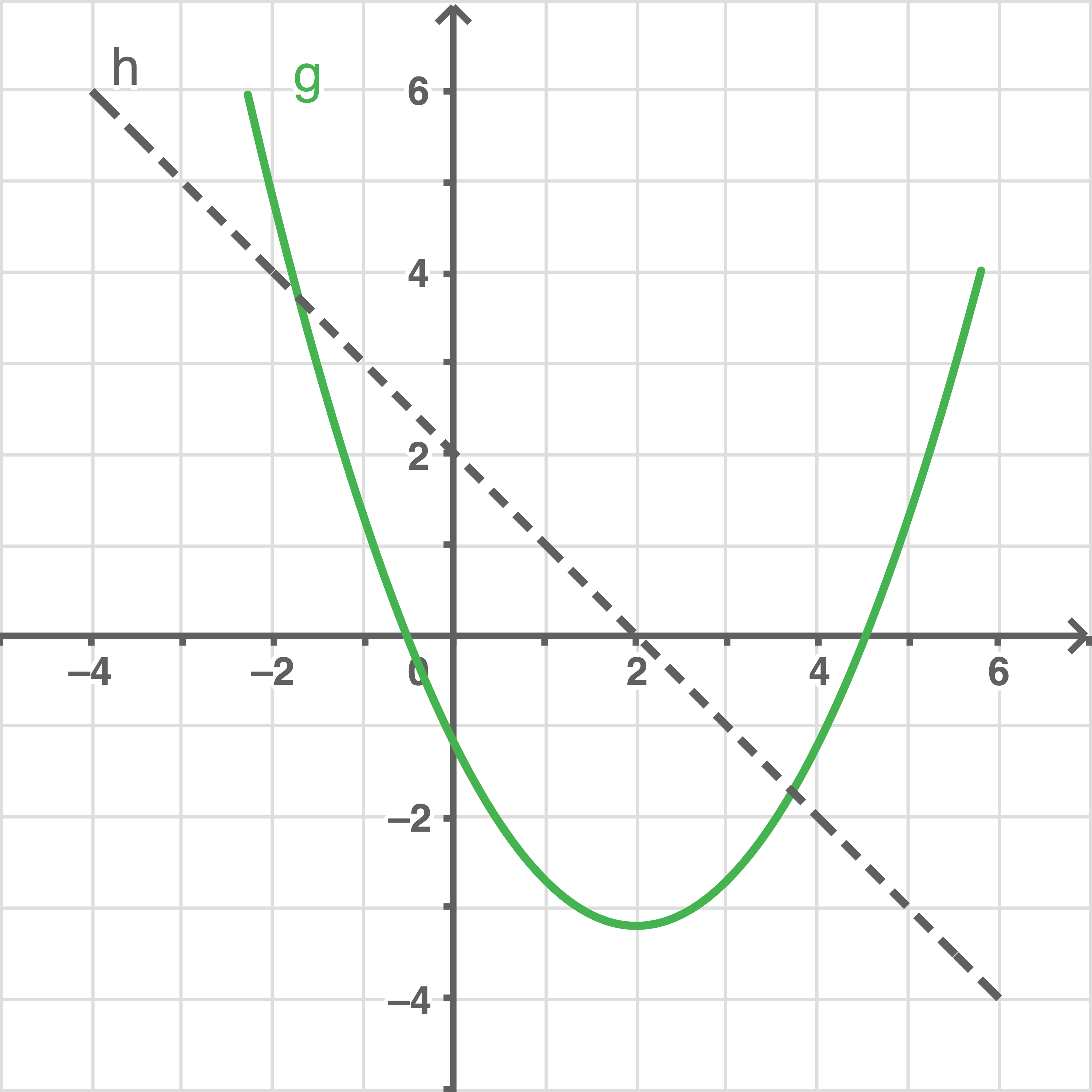
Beurteile, ob die Graphen und
und  die grafischen Darstellungen der ersten und zweiten Ableitungsfunktion dieser Funktion
die grafischen Darstellungen der ersten und zweiten Ableitungsfunktion dieser Funktion  sein können.
sein können.
Beurteile, ob die Graphen
(2 BE)
3
Eine zum Koordinatensystem symmetrische Funktion dritten Grades  hat an der Stelle
hat an der Stelle  die Tangente
die Tangente  mit
mit 

Ermittle eine Gleichung der Funktion
Ermittle eine Gleichung der Funktion
(3 BE)
4
Die Punkte  mit
mit  liegen auf einer Geraden
liegen auf einer Geraden 
a)
Gib eine Parametergleichung für die Gerade  an.
an.
Beschreibe die Lage dieser Geraden im Koordinatensystem.
Beschreibe die Lage dieser Geraden im Koordinatensystem.
(2 BE)
b)
Bestimme einen Wert für  so, dass die Punkte
so, dass die Punkte 
 und
und  ein rechtwinkliges Dreieck mit der Hypotenuse
ein rechtwinkliges Dreieck mit der Hypotenuse  bilden.
bilden.
(3 BE)
5
Eine Urne enthält acht Kugeln, davon sind zwei schwarz und sechs weiß.
a)
Es werden nacheinander drei Kugeln ohne Zurücklegen entnommen.
Berechne die Wahrscheinlichkeit folgender Ergebnisse:




Berechne die Wahrscheinlichkeit folgender Ergebnisse:
„Alle Kugeln sind weiß.“
„Mindestens eine Kugel ist weiß.“
(2 BE)
b)
Der folgende Ausschnitt eines Baumdiagrammes enthält nur die Äste, die zum Ereignis  führen.
führen.
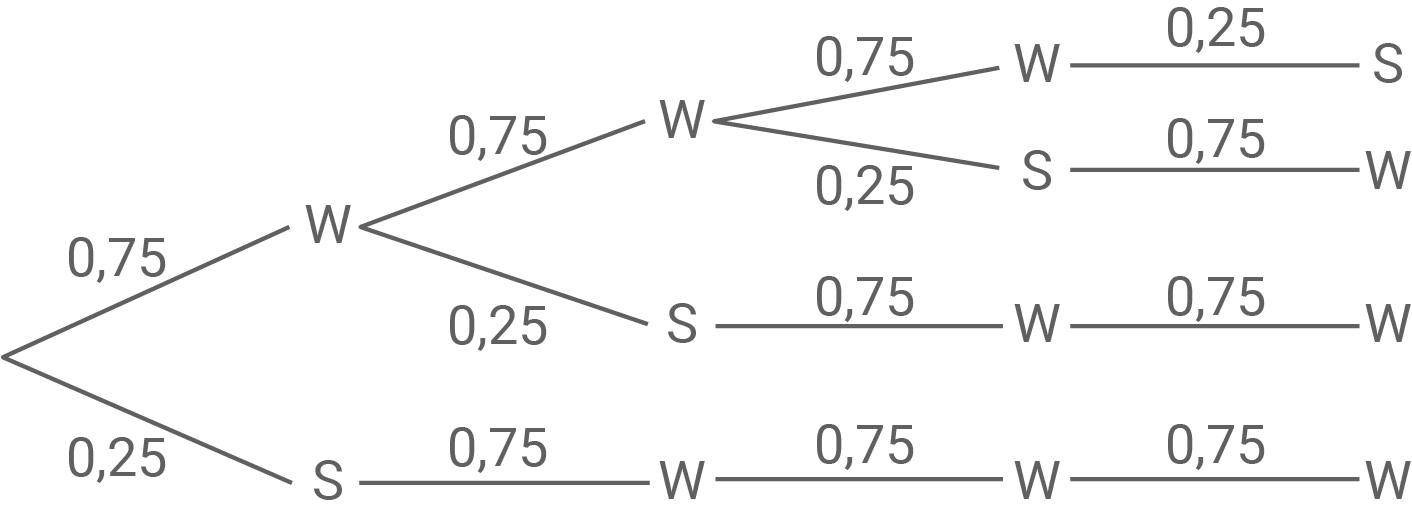 Beschreibe das Zufallsexperiment und das Ereignis
Beschreibe das Zufallsexperiment und das Ereignis  so, dass diese zum Baumdiagramm passen.
so, dass diese zum Baumdiagramm passen.
Gib einen Term zur Berechnung der Wahrscheinlichkeit des Ereignisses an.
an.

Gib einen Term zur Berechnung der Wahrscheinlichkeit des Ereignisses
(3 BE)
1.
a)
Einsetzen von
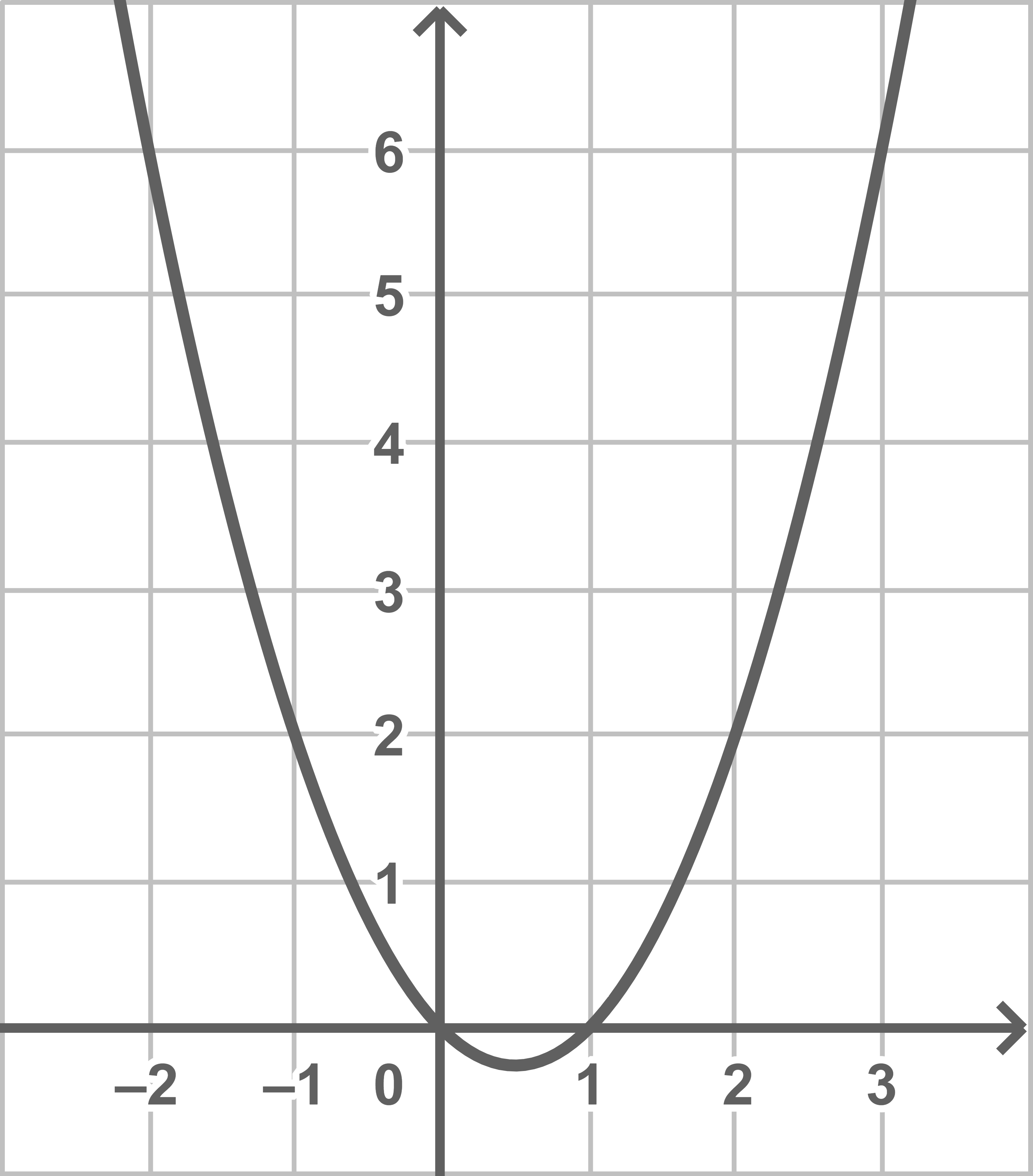
b)
Mit den beiden Nullstellen von  als Integrationsgrenzen folgt für den gesuchten Flächeninhalt:
Der Graph von
als Integrationsgrenzen folgt für den gesuchten Flächeninhalt:
Der Graph von  schließt mit der
schließt mit der  -Achse somit eine Fläche der Größe
-Achse somit eine Fläche der Größe  ein.
ein.
c)
Der Graph von  geht aus dem von
geht aus dem von  durch Streckung in
durch Streckung in  -Richtung hervor, das heißt es gilt
-Richtung hervor, das heißt es gilt  für
für  Der Graph von
Der Graph von  hat somit die gleichen Nullstellen wie der Graph von
hat somit die gleichen Nullstellen wie der Graph von  und mit dem Ergebnis aus Aufgabenteil b) folgt:
und mit dem Ergebnis aus Aufgabenteil b) folgt:
![\(\begin{array}[t]{rll}
A_g&=& \dfrac{1}{2} \\[5pt]
\left|\displaystyle\int_{0}^{1}a\cdot f(x)\;\mathrm dx \right|&=& \dfrac{1}{2} \\[5pt]
a\cdot \left|\displaystyle\int_{0}^{1}f(x)\;\mathrm dx \right|&=&\dfrac{1}{2} \\[5pt]
a\cdot\dfrac{1}{6}&=& \dfrac{1}{2} &\quad \scriptsize \mid\;\cdot 6\\[5pt]
a&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/8171561fb01e6ed7bdb2c747db3638db30195f4691b98dd781e8ece3bbd9f904_light.svg) Eine Funktionsgleichung von
Eine Funktionsgleichung von  ist somit gegeben durch
ist somit gegeben durch 
2.
Die Funktion  ist eine ganzrationale Funktion dritten Grades. Die erste Ableitung
ist eine ganzrationale Funktion dritten Grades. Die erste Ableitung  hat somit Grad zwei und die zweite Ableitung
hat somit Grad zwei und die zweite Ableitung  Grad eins, das heißt
Grad eins, das heißt  müsste die erste Ableitung sein und
müsste die erste Ableitung sein und  die zweite.
die zweite.
Aus der Abbildung folgt, dass an der Stelle
an der Stelle  eine Nullstelle besitzt, aber
eine Nullstelle besitzt, aber  gilt. Somit ist die hinreichende Bedingung für eine Minimalstelle von
gilt. Somit ist die hinreichende Bedingung für eine Minimalstelle von  bei
bei  nicht erfüllt, das heißt der Graph von
nicht erfüllt, das heißt der Graph von  könnte zwar die graphische Darstellung von
könnte zwar die graphische Darstellung von  sein, der Graph von
sein, der Graph von  allerdings nicht die von
allerdings nicht die von 
Aus der Abbildung folgt, dass
3.
Die Funktion  ist eine zum Koordinatensystem symmetrische Funktion dritten Grades, das heißt besitzt nur ungerade Exponenten und ist somit der Form
ist eine zum Koordinatensystem symmetrische Funktion dritten Grades, das heißt besitzt nur ungerade Exponenten und ist somit der Form  Für die erste Ableitung von
Für die erste Ableitung von  folgt:
folgt:
 Die Tangente
Die Tangente  berührt den Graphen von
berührt den Graphen von  im Punkt
im Punkt  Mit der Steigung
Mit der Steigung  der Tangente folgt somit
der Tangente folgt somit  zudem folgt durch Einsetzen von
zudem folgt durch Einsetzen von  in
in 
 Es ergibt sich folgendes Gleichungssystem:
Es ergibt sich folgendes Gleichungssystem:
 Die zweite Zeile liefert
Die zweite Zeile liefert  Einsetzen in die erste Zeile ergibt:
Einsetzen in die erste Zeile ergibt:
![\(\begin{array}[t]{rll}
3a+1-a&=&-2 &\quad \scriptsize \mid\; -1 \\[5pt]
2a&=&-3 &\quad \scriptsize \mid\; :2 \\[5pt]
a&=&-\dfrac{3}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/74fb648093dc9bed227a47a9c480ed23eb05f1377a9e8a6c6f89de9929fe8d71_light.svg) Damit folgt für
Damit folgt für 
 Eine Funktionsgleichung von
Eine Funktionsgleichung von  lautet somit
lautet somit 
4.
a)
Parametergleichung angeben

 Eine Gleichung der Geraden
Eine Gleichung der Geraden  lautet somit wie folgt:
lautet somit wie folgt:
 Lage im Koordinatensystem beschreiben
Die
Lage im Koordinatensystem beschreiben
Die  -Koordinate des Richtungsvektors ist Null, das heißt alle Punkte
-Koordinate des Richtungsvektors ist Null, das heißt alle Punkte  haben die gleiche
haben die gleiche  -Koordinate, und
-Koordinate, und  liegt somit parallel zur
liegt somit parallel zur  -Ebene.
-Ebene.
b)
Ein rechtwinkliges Dreieck  mit der Strecke
mit der Strecke  als Hypotenuse besitzt den rechten Winkel im Punkt
als Hypotenuse besitzt den rechten Winkel im Punkt  das heißt zwischen den Strecken
das heißt zwischen den Strecken  und
und  Für die zugehörigen Vektoren folgt:
Für die zugehörigen Vektoren folgt:




 Mit dem Skalarprodukt dieser beiden Vektoren folgt nun:
Für
Mit dem Skalarprodukt dieser beiden Vektoren folgt nun:
Für  bilden die drei Punkte
bilden die drei Punkte  und
und  somit ein rechtwinkliges Dreieck mit der Hypotenuse
somit ein rechtwinkliges Dreieck mit der Hypotenuse 
5.
a)
b)
Zufallsexperiment und Ereignis  beschreiben
In dem Zufallsexperiment wird viermal aus einer Urne gezogen, da dass Baumdiagramm vier Ebenen hat. Die Wahrscheinlichkeit eine schwarze oder weiße Kugel zu ziehen, bleibt bei jedem Zug gleich und stimmt mit den Anfangswahrscheinlichkeiten aus Aufgabenteil a) überein. Da in jedem Pfad eine weiße und drei Schwarze Kugeln gezogen werden, lautet eine mögliche Beschreibung des Zufallsexperiments und des Ereignisses
beschreiben
In dem Zufallsexperiment wird viermal aus einer Urne gezogen, da dass Baumdiagramm vier Ebenen hat. Die Wahrscheinlichkeit eine schwarze oder weiße Kugel zu ziehen, bleibt bei jedem Zug gleich und stimmt mit den Anfangswahrscheinlichkeiten aus Aufgabenteil a) überein. Da in jedem Pfad eine weiße und drei Schwarze Kugeln gezogen werden, lautet eine mögliche Beschreibung des Zufallsexperiments und des Ereignisses  wie folgt:
wie folgt:
Aus der in der Aufgabenstellung gegebenen Urne wird viermal mit Zurücklegen eine Kugel gezogen und Ereignis ist, dass dabei genau eine schwarze Kugel gezogen wird.
Term zur Berechnung der Wahrscheinlichkeit angeben
Die Zufallsvariable
ist, dass dabei genau eine schwarze Kugel gezogen wird.
Term zur Berechnung der Wahrscheinlichkeit angeben
Die Zufallsvariable  beschreibt die Anzahl der schwarzen Kugeln, die bei vier Zügen mit Zurücklegen gezogen werden.
beschreibt die Anzahl der schwarzen Kugeln, die bei vier Zügen mit Zurücklegen gezogen werden.  ist binomialverteilt mit den Parametern
ist binomialverteilt mit den Parametern  und
und  da die Wahrscheinlichkeit für eine schwarze Kugel pro Zug gleichbleibt und es nur zwei mögliche Ergebnisse pro Zug gibt. Mit der Formel für die Binomialverteilung folgt:
da die Wahrscheinlichkeit für eine schwarze Kugel pro Zug gleichbleibt und es nur zwei mögliche Ergebnisse pro Zug gibt. Mit der Formel für die Binomialverteilung folgt:
![\(\begin{array}[t]{rll}
P(C)&=&B_{4;0,25}(X=1) \\[5pt]
&=&\pmatrix{4\\1}\cdot 0,25^1\cdot 0,75^{4-1} \\[5pt]
&=& 4\cdot 0,25\cdot 0,75^3 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/80dddbb4c6b181056b3b2f2fc5279abde9518f1ee7ad9cf3969b28e4c9843ca1_light.svg) Die Wahrscheinlichkeit von Ereignis
Die Wahrscheinlichkeit von Ereignis  lässt sich somit mit dem Term
lässt sich somit mit dem Term  berechnen.
berechnen.
Aus der in der Aufgabenstellung gegebenen Urne wird viermal mit Zurücklegen eine Kugel gezogen und Ereignis