Teil C1
1
Der Diamant ist eine Modifikation des Kohlenstoffes und bildet meist oktaederförmige Kristalle. Oktaeder sind quadratische Doppelpyramiden mit 12 gleich langen Kanten. Betrachtet werden diese geraden quadratischen Pyramiden mit der gemeinsamen Grundfläche 
und den Koordinaten der Eckpunkte 
und 
a)
Gib die Koordinaten des Punktes 
an.
(1 BE)
b)
Die Punkte 
und 
bilden jeweils die Spitze der Pyramiden und liegen auf einer Geraden 
die durch den Mittelpunkt der Grundfläche verläuft.
Gib eine Gleichung für die Gerade
an.
Gib eine Gleichung für die Gerade
(1 BE)
c)
Berechne die Koordinaten der Punkte und 
Zeichne das Oktaeder
in ein kartesisches Koordinatensystem.
[Kontrollergebnis:
]
Zeichne das Oktaeder
[Kontrollergebnis:
(4 BE)
d)
Auf der Kante 
liegt ein Punkt 
der die Strecke im Verhältnis 
teilt.
Bestimme die Koordinaten von
Bestimme die Koordinaten von
(2 BE)
e)
Der größte je gefundene Diamant namens „Cullinan“ wurde 1950 in einer Mine in Südafrika ausgegraben und später in 105 Steine aufgespalten. Seine Masse betrug 3106,7 Karat 
Gib die Masse des Diamanten in
an.
Gib die Masse des Diamanten in
(1 BE)
f)
Die größten Diamantstücke wurden zu britischen Kronjuwelen verarbeitet.
Das oben beschriebene Oktaeder ist nun ein Modell eines solchen Diamantstücks. Bei ist nun ein Modell eines solchen Diamantstücks. Bei diesem wird durch ein Punkt
(aus Aufgabe d) parallel zur Grundfläche der quadratischen Pyramide 
der obere Teil der Pyramide abgetrennt.
Berechne den prozentualen Anteil des abgetrennten Teils vom gesamten Oktaeder
Das oben beschriebene Oktaeder ist nun ein Modell eines solchen Diamantstücks. Bei ist nun ein Modell eines solchen Diamantstücks. Bei diesem wird durch ein Punkt
Berechne den prozentualen Anteil des abgetrennten Teils vom gesamten Oktaeder
(3 BE)
2
In einem Betrieb werden Glaskugeln in großer Stückzahl als Weihnachtsbaumschmuck hergestellt. Sie werden in vier Arbeitsgängen gefertigt und nach der Fertigstellung geprüft. Erfahrungsgemäß wird in den einzelnen Arbeitsgängen unabhängig voneinander die erwünschte Qualität für 
Wahl mit folgenden Wahrscheinlichkeiten erreicht:
Eine fertige Glaskugel gilt nur dann als Wahl, wenn in jedem Arbeitsgang die Qualität für Wahl erreicht wurde.
| Arbeitsgang 1 | 97 % |
|---|---|
| Arbeitsgang 2 | 92 % |
| Arbeitsgang 3 | 93 % |
| Arbeitsgang 4 | 97 % |
a)
Zeige, dass das Ereignis „Eine fertige Glaskugel ist nicht Wahl“ mit einer Wahrscheinlichkeit von 
eintritt.
(1 BE)
b)
Die Zufallsvariable 
beschreibt die Anzahl der Glaskugeln in einer Produktionsserie, die nicht Wahl sind.
Gib mindestens zwei Gründe dafür an, dass man als binomialverteilt ansehen kann.
Gib mindestens zwei Gründe dafür an, dass man
(2 BE)
c)
Bestimme unter der Annahme, dass das Modell der Binomialverteilung genutzt werden kann, die Wahrscheinlichkeit folgender Ereignisse.
„Von zehn hergestellten Glaskugeln sind höchstens zwei nicht Wahl.“
„Von 100 hergestellten Glaskugeln sind mindestens 80 Glaskugeln Wahl.“
(2 BE)
d)
Im Betrieb wurden die Produktionsverfahren verbessert. Der Verantwortliche für Qualitätssicherung vermutet nun, dass nur noch 
(
) statt bisher 
(
) der Kugeln nicht Wahl sind. Die möchte er an einer Packung mit 100 Kugeln überprüfen. Findet er dabei höchstens 12 fehlerhafte Kugeln, so hält er seine Hypothese für bestätigt.
Berechne die Wahrscheinlichkeit, mit der er zu Unrecht an eine bessere Qualität glaubt.
Berechne die Wahrscheinlichkeit, mit der er zu Unrecht an eine bessere Qualität glaubt.
(3 BE)
1.
a)
b)
Für den Mittelpunkt der Grundfläche folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt]
&=&\pmatrix{5 \\ 3 \\ 1}+\dfrac{1}{2} \cdot \pmatrix{1-5 \\ 7-3 \\ 1-1}\\[5pt]
&=& \pmatrix{3 \\ 5 \\ 1}
\end{array}\)](https://mathjax.schullv.de/b233539b74020668272cccbd32af383721b3838763293e284331147df4b41644?color=5a5a5a)
Ein Normalenvektor der Ebene, in der die Grundfläche liegt, ergibt sich mit Hilfe des CAS wie folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{n} &=& \overrightarrow{BC} \times\overrightarrow{CA} \\[5pt]
&=& \pmatrix{-4 \\ 0 \\ 0} \times \pmatrix{4 \\ -4 \\ 0} \\[5pt]
&=& \pmatrix{0 \\ 0 \\ 16}
\end{array}\)](https://mathjax.schullv.de/8516a2e091ba51376e4c15c9644a79183a48d8df6fdf9bae4c9279cc2d2f96d4?color=5a5a5a)
Mit dem saklierten Normalenvektor 
folgt die gesuchte Geradengleichung somit:
c)
Koordinaten der Punkte 
und 
berechnen
Die Punkte und liegen beide auf der, in Aufgabenteil b) bestimmten, Geraden 
Da die Gerade orthogonal zu der Fläche steht, ist 
ein rechtwinkliges Dreieck. Für die Länge der Seite 
folgt mit dem CAS:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{AM}\right\vert &=& \left\vert\pmatrix{3-5 \\ 5-3 \\ 1-1}\right\vert \\[5pt]
&=& \sqrt{8}
\end{array}\)](https://mathjax.schullv.de/85d6830c67e78e61ed9a797d2d07b47c73c173249cf6533b07191717adff9b95?color=5a5a5a)
Da die Kanten eines Oktaeders gleich lang sind, folgt für die Länge der Kante 
mit dem CAS:
Mit dem Satz des Pythagoras ergibt sich nun die Länge von 
im CAS:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{ME}\right\vert&=&\sqrt{\left\vert\overrightarrow{EA}\right\vert^2-\left\vert\overrightarrow{AM}\right\vert^2} \\[5pt]
&=& \sqrt{8}
\end{array}\)](https://mathjax.schullv.de/75f01c99834d8b8e0cf8137515f706c1ac08d3071205e0dfb24f44a8bc95216f?color=5a5a5a)
Da der Spannvektor der Geraden einen Betrag von 
besitzt, liefert einsetzen von 
in die Geradengleichung von den Punkt 
![\(\begin{array}[t]{rll}
\overrightarrow{OE}&=& \pmatrix{3 \\ 5 \\ 1} + \sqrt{8} \cdot \pmatrix{0 \\ 0 \\ 1}\\[5pt]
&=& \pmatrix{3 \\ 5 \\ 1+\sqrt{8}}
\end{array}\)](https://mathjax.schullv.de/3d0b53ef6b1e3398d665841cad300695e6d25c11cf2a036d06d1d2ca4c71054c?color=5a5a5a)
Da der Punkt im gleichen Abstand zu und auch auf der Geraden liegt, liefert Einsetzen von 
den zugehörigen Ortsvektor:
![\(\begin{array}[t]{rll}
\overrightarrow{OF}&=& \pmatrix{3 \\ 5 \\ 1} - \sqrt{8} \cdot \pmatrix{0 \\ 0 \\ 1}\\[5pt]
&=& \pmatrix{3 \\ 5 \\ 1-\sqrt{8}}
\end{array}\)](https://mathjax.schullv.de/4534569f636bdea2c49c01f4daa42eb56730860e8bbdda55a8832876500f2a78?color=5a5a5a)
Die Koordinaten der Punkte bzw. sind somit gegeben durch 
bzw. 
Oktaeder zeichnen
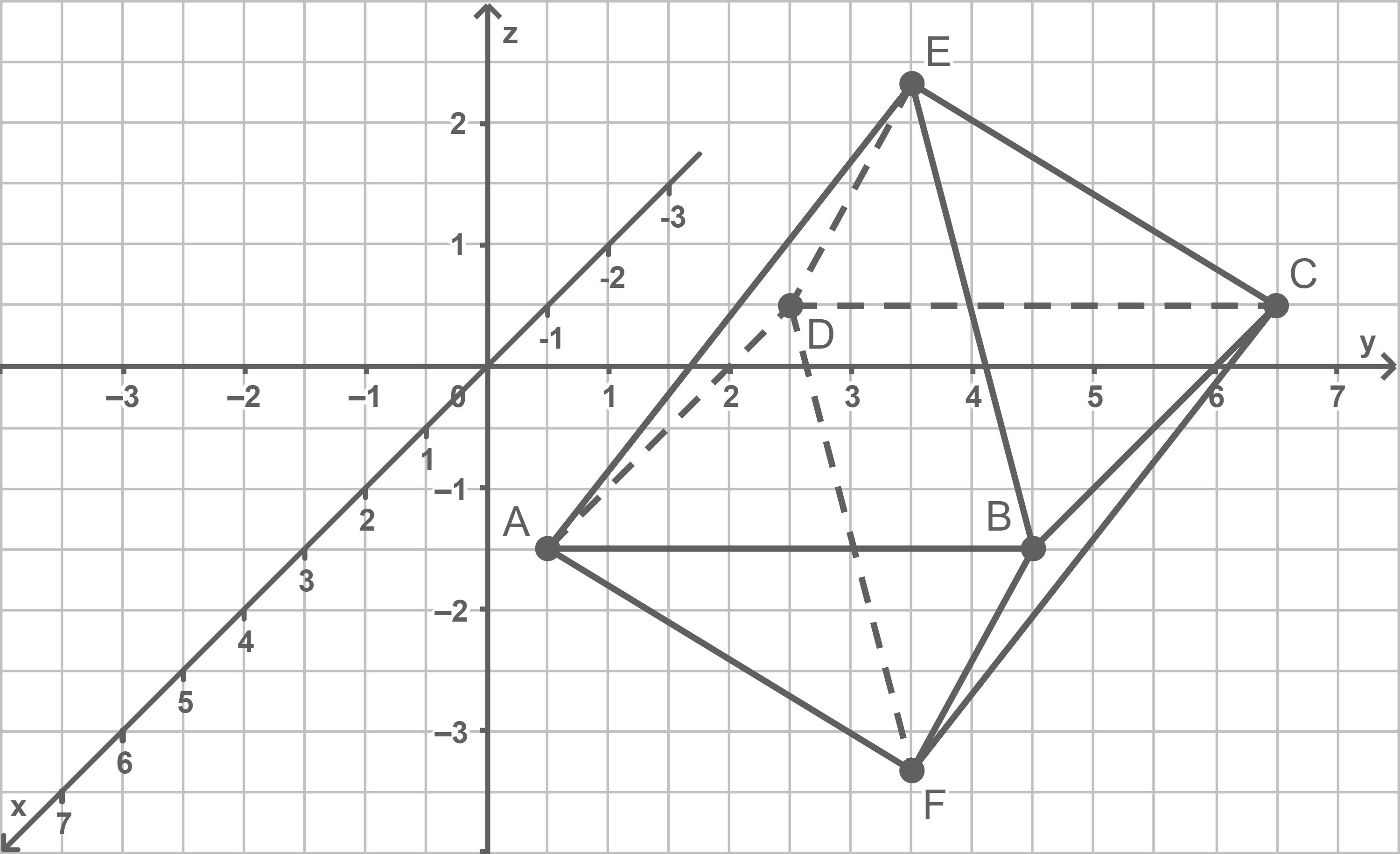
d)
Da der Punkt die Kante im Verhältnis 
teilt, ergibt sich der Ortsvektor von durch Addition von 
zum Ortsvektor von 
Mit dem CAS folgt:
Die Koordinaten von sind somit gegeben durch 
e)
f)
Der abgetrennte Teil ist eine kleine Pyramide, die zur oberen Pyramide des Oktaeders ähnlich ist. Da die Strecke 
im Verhältnis 
teilt, ergibt sich der Längenfaktor 
Mit diesem Längenfaktor ergibt sich das Verhältnis zwischen dem Volumen 
der oberen Pyramide des Oktaeders und dem Volumen 
der abgetrennten Pyramide wie folgt:
Da der Oktaeder aus zwei Pyramiden mit Volumen besteht, folgt weiter:
Der abgetrennte Teil beträgt damit 
des gesamten Oktaeders
2.
a)
„Eine fertige Glaskugel ist nicht 
Wahl“
Für die Wahrscheinlichkeit des Gegenereignisses folgt mit der Pfadmultiplikationsregel:
b)
- Die Qualität einer Kugel ist unabhängig von der anderer Kugeln.
- Beim Überprüfen einer fertigen Kugel gibt es genau zwei Ergebnisse, nämlich
- Wegen der großen Stückzahl ist der Unterschied zwischen Ziehen mit Zurücklegen und Ziehen ohne Zurücklegen vernachlässigbar, das heißt es kann von konstanten Wahrscheinlichkeiten ausgegangen werden
c)
Die Zufallsvariable beschreibt die Anzahl der Glaskugeln in einer Produktionsserie, die nicht Wahl sind, und ist binomialverteilt mit den Parametern 
und 
für Ereignis 
sowie mit 
und für Ereignis 
Mit dem CAS folgt:
![\(\begin{array}[t]{rll}
P(A)&=&B_{10;0,195}(X\leq2) \\[5pt]
&\approx&0,6928 \\[5pt]
&=&69,28\,\%
\end{array}\)](https://mathjax.schullv.de/209609bcda16a54a98ce9086cd88e7c11423466ad3b1f902bf68ddcad0f4629d?color=5a5a5a)
![\(\begin{array}[t]{rll}
P(B)&=&B_{100;0,195}(X\leq20) \\[5pt]
&\approx&0,6088 \\[5pt]
&=&60,88\,\%
\end{array}\)](https://mathjax.schullv.de/c9ed9c79df147747d56e082e8de16ecb4f8cded7fd8e17d65a19e2e750fae319?color=5a5a5a)
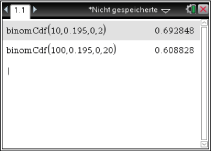
d)
Die Wahrscheinlichkeit, mit der der Verantwortliche zu Unrecht an eine bessere Qualität glaubt, entspricht dem 
-Fehler.
Aus der Aufgabenstellung ergibt sich der Verwerfungsbereich
für die Nullhypothese. Für die gesuchte Wahrscheinlichkeit folgt somit, wenn die mit den Parametern und 
binomialverteilte Zufallsgröße ist, die die Anzahl der Kugeln die nicht Wahl sind angibt, mit dem CAS:
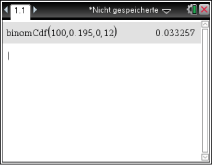
Aus der Aufgabenstellung ergibt sich der Verwerfungsbereich
1.
a)
b)
Für den Mittelpunkt der Grundfläche folgt:
Ein Normalenvektor der Ebene, in der die Grundfläche liegt, ergibt sich mit Hilfe des CAS wie folgt:
Mit dem saklierten Normalenvektor folgt die gesuchte Geradengleichung somit:
c)
Koordinaten der Punkte und berechnen
Die Punkte und liegen beide auf der, in Aufgabenteil b) bestimmten, Geraden Da die Gerade orthogonal zu der Fläche steht, ist ein rechtwinkliges Dreieck. Für die Länge der Seite folgt mit dem CAS:
Da die Kanten eines Oktaeders gleich lang sind, folgt für die Länge der Kante mit dem CAS:
Mit dem Satz des Pythagoras ergibt sich nun die Länge von im CAS:
Da der Spannvektor der Geraden einen Betrag von besitzt, liefert einsetzen von in die Geradengleichung von den Punkt
Da der Punkt im gleichen Abstand zu und auch auf der Geraden liegt, liefert Einsetzen von den zugehörigen Ortsvektor:
Die Koordinaten der Punkte bzw. sind somit gegeben durch bzw.
Oktaeder zeichnen
d)
Da der Punkt die Kante im Verhältnis teilt, ergibt sich der Ortsvektor von durch Addition von zum Ortsvektor von Mit dem CAS folgt:
Die Koordinaten von sind somit gegeben durch
e)
f)
Der abgetrennte Teil ist eine kleine Pyramide, die zur oberen Pyramide des Oktaeders ähnlich ist. Da die Strecke im Verhältnis teilt, ergibt sich der Längenfaktor Mit diesem Längenfaktor ergibt sich das Verhältnis zwischen dem Volumen der oberen Pyramide des Oktaeders und dem Volumen der abgetrennten Pyramide wie folgt:
Da der Oktaeder aus zwei Pyramiden mit Volumen besteht, folgt weiter:
Der abgetrennte Teil beträgt damit des gesamten Oktaeders
2.
a)
„Eine fertige Glaskugel ist nicht Wahl“
Für die Wahrscheinlichkeit des Gegenereignisses folgt mit der Pfadmultiplikationsregel:
b)
- Die Qualität einer Kugel ist unabhängig von der anderer Kugeln.
- Beim Überprüfen einer fertigen Kugel gibt es genau zwei Ergebnisse, nämlich
- Wegen der großen Stückzahl ist der Unterschied zwischen Ziehen mit Zurücklegen und Ziehen ohne Zurücklegen vernachlässigbar, das heißt es kann von konstanten Wahrscheinlichkeiten ausgegangen werden
c)
Die Zufallsvariable beschreibt die Anzahl der Glaskugeln in einer Produktionsserie, die nicht Wahl sind, und ist binomialverteilt mit den Parametern und für Ereignis sowie mit und für Ereignis Mit dem CAS folgt:
d)
Die Wahrscheinlichkeit, mit der der Verantwortliche zu Unrecht an eine bessere Qualität glaubt, entspricht dem -Fehler.
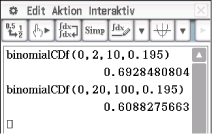
Aus der Aufgabenstellung ergibt sich der Verwerfungsbereich für die Nullhypothese. Für die gesuchte Wahrscheinlichkeit folgt somit, wenn die mit den Parametern und binomialverteilte Zufallsgröße ist, die die Anzahl der Kugeln die nicht Wahl sind angibt, mit dem CAS:
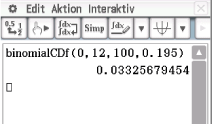
Aus der Aufgabenstellung ergibt sich der Verwerfungsbereich