Teil A

Gegeben ist die Funktion $f$ durch $f(x)=x^3-3x+2$ $(x\in\mathbb{R}).$

Zeige, dass $t(x)=-3x+2$ eine Gleichung der Tangente an den Graphen von $f$ im Punkt $P\left(0\mid f(0)\right)$ ist.

(2 BE)

Gib eine Gleichung der Normalen an den Graphen von $f$ im Punkt $P\left(0\mid f(0)\right)$ an.

(1 BE)

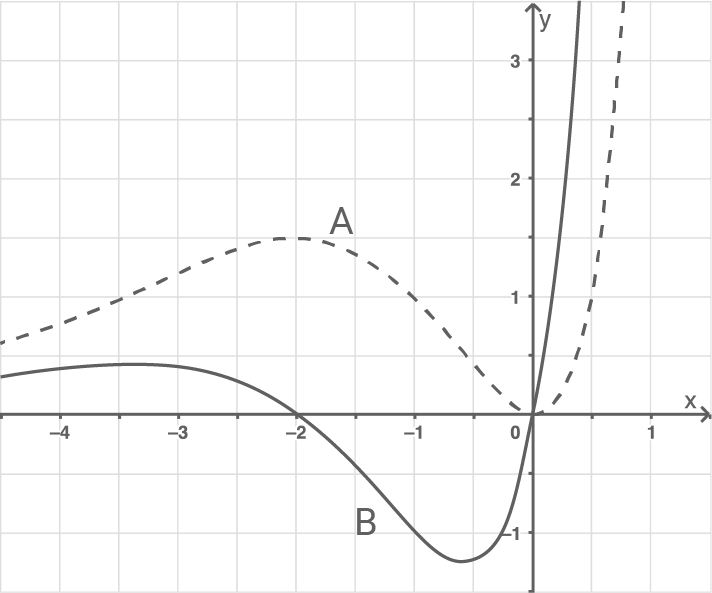
Dargestellt sind die Graphen einer Funktion $f$ und ihrer Ableitungsfunktion $\(f$
Ordne den Funktionen die abgebildeten Graphen $A$ und $B$ zu.
Begründe deine Zuordnung.

thüringen mathe abi 2015 teil a abbildung 1

(2 BE)

Für jede reelle Zahl $a$ ist eine Funktion $f_a$ in ihrem größtmöglichen Definitionsbereich durch $f_a(x)=\dfrac{x^2-2}{x+a}$ gegeben.

Gib den Wert für $a$ so an, dass der Graph von $f_a$ eine Asymptote mit der Gleichung $x=3$ besitzt.

(1 BE)

Begründe, dass der Graph von $f_a$ für $a=0$ eine schräge Asymptote hat.

(1 BE)

Gegeben ist die Funktion $f$ durch $f(x)=-2x+2$ $(x\in\mathbb{R}).$

Bestimme alle Stammfunktionen von $f,$ die nur negative Funktionswerte besitzen.

(2 BE)

Der Graph der Funktion $f$ schließt mit den Koordinatenachsen die Fläche $A$ vollständig ein.
Gib den Flächeninhalt von $A$ an.

(1 BE)

Gegeben ist die Strecke $\overline{AB}$ durch die Punkte $A(1\mid-2\mid3)$ und $B(4\mid4\mid9).$

Berechne die Länge der Strecke $\overline{AB}.$

(1 BE)

Prüfe, ob der Punkt $C(0\mid-4\mid1)$ auf der Strecke $\overline{AB}$ liegt.

(2 BE)

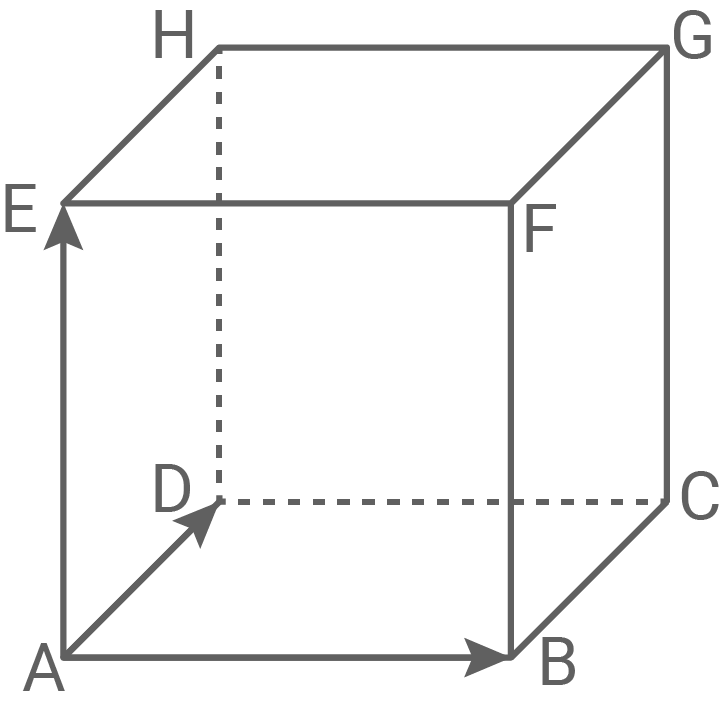
In einem Würfel sind die Vektoren $\vec{a}=\overrightarrow{AB}$ , $\vec{b}=\overrightarrow{AD}$ und $\vec{c}=\overrightarrow{AE}$ gegeben.
Der Punkt $S$ ist der Schnittpunkt der Diagonalen der Seitenfläche $ADHE$ .
Gib die Vektoren $\overrightarrow{AC}$ und $\overrightarrow{SB}$ mit Hilfe der Vektoren $\vec{a}$ , $\vec{b}$ und $\vec{c}$ an.

thüringen mathe abi 2015 teil a abbildung 2 würfel

(2 BE)

Für einen Multiple-Choice-Test werden zu 32 Fragen je vier mögliche Antworten vorgegeben, von denen genau eine richtig ist. Der Test gilt als bestanden, wenn ein Teilnehmer mehr als 30 Fragen richtig beantwortet. Max kreuzt zufällig und ohne Kenntnisse pro Frage eine Antwort an.

Gib den Erwartungswert für die Anzahl der richtigen Antworten an.

(1 BE)

Ordne den Ereignissen $A,$ $B$ und $C$ die entsprechenden Gleichungen zur Berechnung der Wahrscheinlichkeit zu.

$A:$ $=$

„Max hat alle Fragen falsch beantwortet.“

$B:$ $=$

„Max besteht den Test.“

$C:$ $=$

„Max hat nur die erste Frage richtig beantwortet.“

$p_1=\left(\dfrac{3}{4}\right)^{32}$

$p_2=\left(\dfrac{1}{4}\right)^1\cdot\left(\dfrac{3}{4}\right)^{31}$

$p_3=32\cdot\left(\dfrac{1}{4}\right)^{31}\cdot\left(\dfrac{3}{4}\right)^{1}+\left(\dfrac{1}{4}\right)^{32}$

(2 BE)

In einer Schule sind $20\,\%$ der Schüler Linkshänder. $10\,\%$ der Linkshänder spielen Volleyball. Von den Rechtshändern spielen $30\,\%$ Volleyball. Ein Schüler der Schule wird zufällig ausgewählt.
Ermittle die Wahrscheinlichkeit folgender Ereignisse:

$A:$ $=$

„Der ausgewählte Schüler ist ein Rechtshänder und spielt Volleyball.“

$B:$ $=$

„Der ausgewählte Schüler spielt nicht Volleyball.“

(2 BE)

Die Steigung $m$ der gesuchten Tangente $t(x)=mx+b$ ist gegeben als die Steigung von $f$ an der Stelle $x=0.$ Für die erste Ableitung von $f$ folgt:

$\(f$

Einsetzen von $x=0$ in $\(f$ liefert:

$\(\begin{array}[t]{rll} m&=&f$

Mit Hilfe der Rechnung $f(0)=0^3-3\cdot0+2=2$ folgt für die Koordinaten des Punktes $P$ direkt $P(0\mid2).$ Einsetzen dieser Koordinaten in der Tangentengleichung $t(x)=-3x+b$ liefert für $b:$

$\begin{array}[t]{rll} 2&=&-3\cdot0+b \\[5pt] 2&=&b \end{array}$

Die Gleichung der gesuchten Tangente ist somit gegeben durch $t(x)=-3x+2.$

Nach Aufgabenteil a) ist die Tangentengleichung im Punkt $P$ gegeben durch $t(x)=-3x +2.$ Die gesuchte Normale besitzt somit die Steigung $-\frac{1}{-3} = \frac{1}{3}.$

Die allgemeine Normalengleichung hat damit die Form $n(x)=\frac{1}{3}x+c.$ Einsetzen der Koordinaten von $P$ in $n(x)$ liefert für $c:$

$\begin{array}[t]{rll} 2&=&\frac{1}{3}\cdot 0+c \\[5pt] 2&=&c \end{array}$

Die vollständige Normalengleichung lautet somit $n(x)=\frac{1}{3}x +2.$

An den Stellen, wo der Graph $A$ Extremstellen besitzt, besitzt der Graph $B$ Nullstellen. Die Funktionswerte des Graphen $B$ wechseln dort zudem das Vorzeichen, sodass die notwendige und hinreichene Bedingung für Extremstellen des Graphen $A$ erfüllt ist. Somit beschreibt der Graph $A$ die Funktion $f$ und der Graph $B$ die Funktion $\(f$

Die Asymptote $x=3$ ist eine senkrechte Asymptote und tritt bei einer gebrochenrationalen Funktion somit dann auf, wenn ihr Nenner Null wird. Betrachtung des Nenners von $f_a(x)$ an der Stelle $x=3$ liefert somit für den gesuchten Wert von $a:$

$\begin{array}[t]{rll} 3+a&=&0 &\quad \scriptsize \mid\;-3 \\[5pt] a&=&-3 \end{array}$

Die Funktion $f_0$ ist gegeben durch $f_0(x)=\frac{x^2-2}{x}.$ Der Graph einer Funktion besitzt dann eine schiefe Asymptote, wenn der Grad des Zählers, d.h. die höchste Potenz von $x$ im Zähler, größer als der Grad des Nenners ist.
Da $x^2-2$ Grad zwei besitzt, und $x$ nur Grad eins, hat der Graph von $f_a$ für $a=0$ somit eine schiefe Asymptote.

Bildung der allgemeinen Stammfunktion von $f(x)=-2x+2$ liefert:

$F(x)=-x^2+2x+C$

Da der höchste Exponent von $F$ Grad zwei besitzt und ein negatives Vorzeichen hat, handelt es sich bei dem Graphen von $F$ um eine nach unten geöffnete Parabel. Damit $F(x)$ nur negative Funktionswerte besitzt, muss der Scheitelpunkt somit unterhalb der $y$ -Achse liegen. Mit den allgemeinen Koordinaten $S\left(-\frac{b}{2 \cdot a} \mid c - \frac{b^2}{4 \cdot a}\right)$ des Scheitelpunkts einer Parabel der Form $p(x)=a\cdot x^2+b\cdot x +c$ folgt für $C:$

$\begin{array}[t]{rll} C-\dfrac{2^2}{4\cdot(-1)}&\lt&0 \\[5pt] C+1&\lt&0 &\quad \scriptsize \mid\;-1 \\[5pt] C&\lt&-1 \end{array}$

Alle Stammfunktionen von $f$ der Form $F(x)= -x^2 +2x +C$ mit $C \lt -1$ besitzen damit nur negative Funktionswerte.

Einzeichnen des Graphen von $f$ und der Fläche $A$ in ein Koordinatensystem liefert:

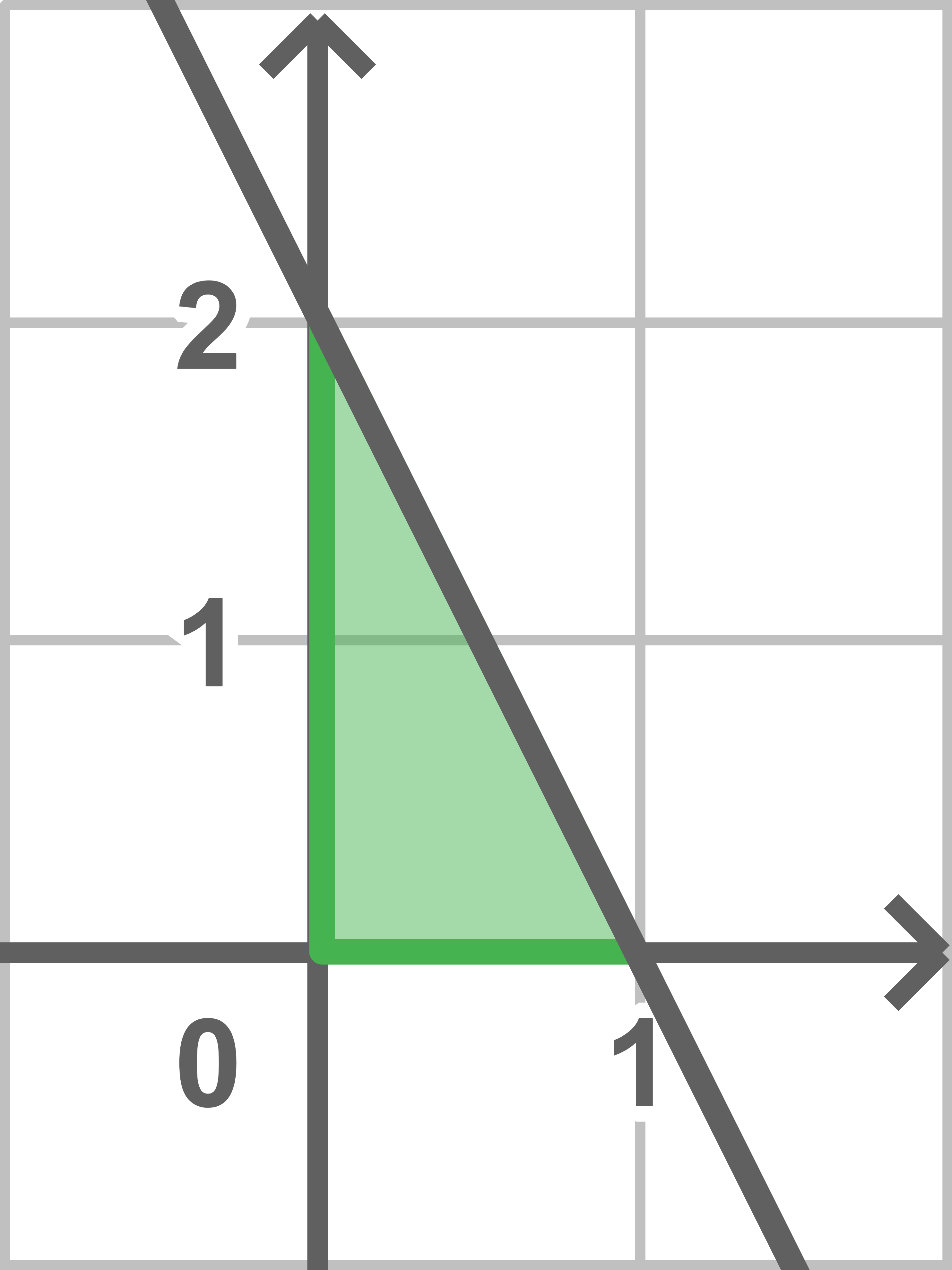Die Fläche $A,$ die der Graph von $f$ mit den Koordinatenachse einschließt, ist somit ein rechtwinkliges Dreieck mit den Kathetenlängen $1\;\text{LE}$ und $2\;\text{LE}.$ Insgesamt ergibt sich damit für den Flächeninhalt von $A:$

$A_A=\dfrac{1}{2}\cdot1\cdot2=1\;[\text{FE}]$

$\begin{array}{rll} \left\vert\overrightarrow{AB}\right\vert&=& \left\vert\pmatrix{4\\4\\9}-\pmatrix{1\\-2\\3}\right\vert \\[5pt] &=&\left\vert\pmatrix{3\\6\\6}\right\vert \\[5pt] &=&\sqrt{(3)^2+(6)^2+(6)^2} \\[5pt] &=&\sqrt{9+36+36} \\[5pt] &=&\sqrt{81} \\[5pt] &=&9 \end{array}$

Mit Hilfe des Ortsvektors von $A$ und dem Vektor $\overrightarrow{AB}$ folgt für die Strecke $\overline{AB}:$

$\overline{AB}: \pmatrix{1\\-2\\3} + \lambda \cdot \pmatrix{3\\6\\6}, \;$ $\lambda \in \left[ 0;1 \right]$

Gleichsetzen mit dem Ortsvektor von $C$ liefert folgendes lineares Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&0&=&1+ 3\lambda &\quad\\ \text{II}\quad&-4&=&-2+ 6\lambda \\ \text{III}\quad&1&=&3+ 6\lambda \\ \end{array}$

Aus Gleichung $\text{I}$ folgt:

$\begin{array}[t]{rll} 0&=&1+3\lambda &\quad \scriptsize \mid\;-3\lambda \\[5pt] -3\lambda&=&1 &\quad \scriptsize \mid\;:(-3) \\[5pt] \lambda&=&-\dfrac{1}{3} \end{array}$

Die einzige mögliche Lösung des Gleichungssystems lautet somit $\lambda = -\frac{1}{3}.$ Da dieser Wert aber nicht im Intervall $\left[0;1\right]$ liegt, liegt der Punkt $C$ nicht auf der Strecke $\overline{AB}.$

$\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$

$\overrightarrow{SB}=\overrightarrow{a} - \dfrac{1}{2} \cdot \overrightarrow{b} - \dfrac{1}{2} \cdot \overrightarrow{c}$

Jede Frage besitzt vier Antwortmöglichkeiten, die Wahrscheinlichkeit, dass Max die richtige Antwort ankreuzt beträgt somit $p=\frac{1}{4}.$ Für den gesuchten Erwartungswert folgt damit:

$\mu = 32\cdot\dfrac{1}{4}=8$

Die Zufallsvariable $X$ gibt die Anzahl der richtigen Antworten von Max an und ist binomialverteilt mit den Parametern $n=32$ und $p=\frac{1}{4}.$ Somit gilt:

$P(X=k)=\pmatrix{n\\k}\cdot p^k \cdot (1-p)^{n-k}$ $=\pmatrix{32\\k}\cdot \left( \dfrac{1}{4} \right)^k \cdot \left(\dfrac{3}{4}\right)^{32-k}$

Ereignis $\boldsymbol{A}$

Die Wahrscheinlichkeit dafür, dass Max alle Fragen falsch beantwortet, ist durch den Fall $k=0$ gegeben. Ein Vergleich mit dem allgemeinen Term liefert somit, dass $p_1$ die zugehörige Wahrscheinlichkeit ist.

Ereignis $\boldsymbol{B}$

Der Test gilt als bestanden, wenn mehr als $30$ der $32$ Fragen richtig beantwortet werden, das heißt $k=31$ oder $k=32$ gilt. Einsetzen in den obigen allgemeinen Term liefert $p_3$ als zugehörige Wahrscheinlichkeit.

Ereignis $\boldsymbol{C}$

Wenn Max nur die erste Frage richtig beantwortet, gilt $k=1.$ Da der Fall $k=1$ aber auch die Wahrscheinlichkeiten enthält, dass Max eine beliebige andere Frage als einzige richtig beantwortet, muss die für $k=1$ mit der allgemeinen Formel für die Binomialverteilung erhaltene Wahrscheinlichkeit noch durch die Anzahl der Fragen, $32,$ geteilt werden. Insgesamt liefert das den Term $p_2.$

$L:$

„Der ausgewählte Schüler ist Linkshänder“

$V:$

„Der ausgewählte Schüler spielt Volleyball“

Wahrscheinlichkeit für Ereignis $\boldsymbol{A}$ ermitteln

Mit der Formel für die bedingte Wahrscheinlichkeit folgt:

Rechenweg anzeigen

$P\left(V \cap \overline{L}\right) = 0,24$

Die Wahrscheinlichkeit, dass ein Schüler Rechtshänder ist und Volleyball spielt, beträgt somit $0,24=24\,\%.$

Wahrscheinlichkeit für Ereignis $\boldsymbol{B}$ ermitteln

Die Formel für die bedingte Wahrscheinlichkeit liefert weiter:

Rechenweg anzeigen

$P\left(V \cap L\right) = 0,02$

Zusammen mit der oben ermittelten Wahrscheinlichkeit für Ereignis $A$ und den Wahrscheinlichkeiten aus der Aufgabenstellung ergibt sich folgende Vierfeldertafel:

	$\color{#ffff}{V}$
$\color{#ffff}{L}$	$0,02$	$0,2$
$\color{#ffff}{\overline{L}}$	$0,24$	$0,8$
	$0,26$	$1$

Für die gesuchte Wahrscheinlichkeit folgt nun aus der unteren Zeile der Vierfeldertafel:

$P\left(\overline{V}\right) = 1-0,26 = 0,74$

Die Wahrscheinlichkeit, dass ein Schüler nicht Volleyball spielt, beträgt somit $0,74=74\,\%.$