Teil A
1
a)
Kreuze jeweils die Aussage an, die richtig ist.



Nullstellen der Funktion  mit
mit  sind:
sind:
Die Polstelle(n) der Funktion  mit
mit  ist (sind):
ist (sind):
Lösung der Gleichung  ist:
ist:
| die leere Menge |
(3 BE)
b)
Ermittle eine Stammfunktion der Funktion  mit
mit 
(2 BE)
2
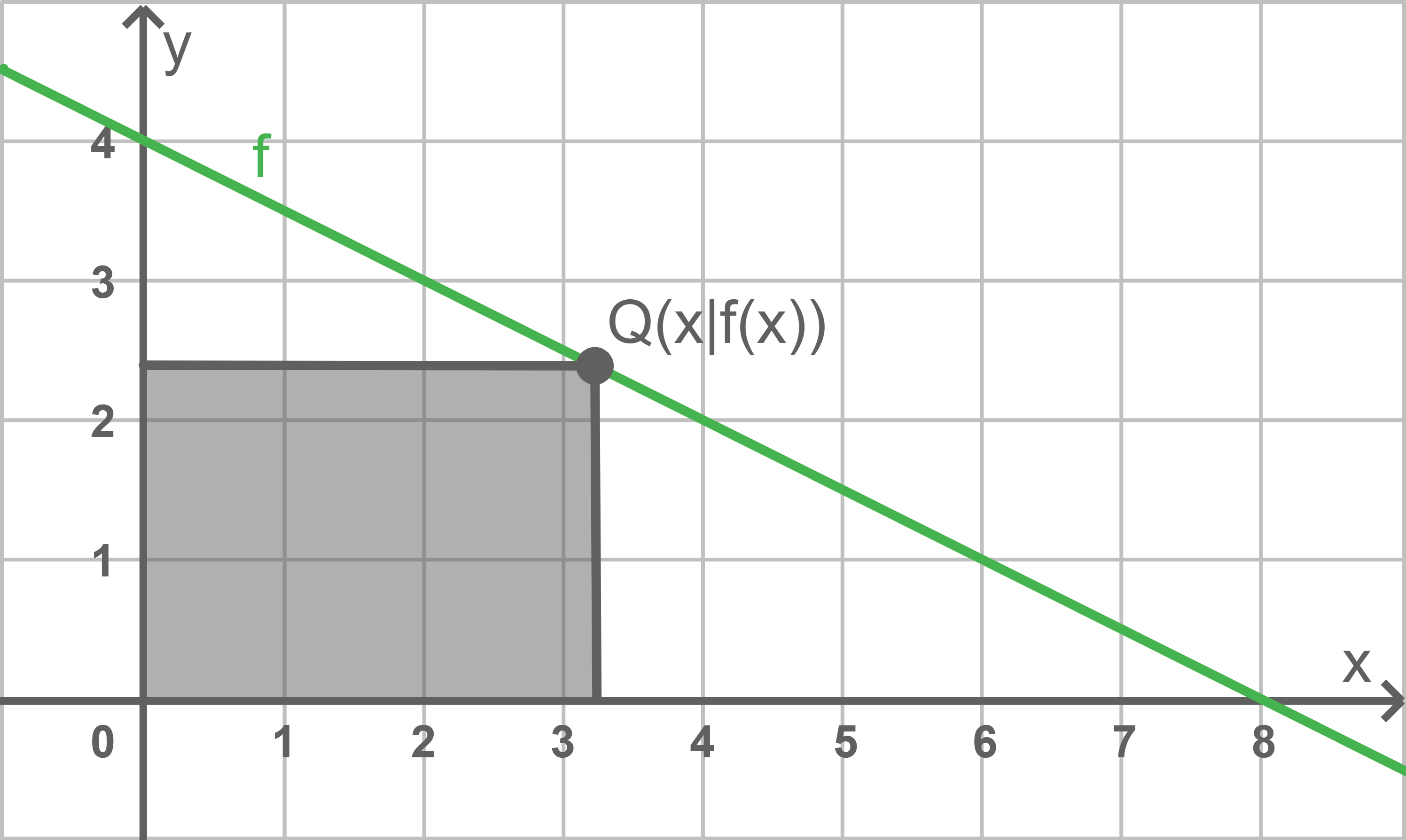
Gegeben ist eine Funktion  durch
durch 

Ein Punkt liegt im
liegt im  Quadranten auf dem Graphen von
Quadranten auf dem Graphen von 
Die Parallelen durch zu den Koordinatenachsen und die Koordinatenachsen begrenzen ein Rechteck.
zu den Koordinatenachsen und die Koordinatenachsen begrenzen ein Rechteck.
Berechne den größtmöglichen Flächeninhalt, den dieses Rechteck besitzen kann.
Ein Punkt
Die Parallelen durch
Berechne den größtmöglichen Flächeninhalt, den dieses Rechteck besitzen kann.
(5 BE)
3
Gegeben ist die Funktion  durch
durch 

a)
Ermittle eine Gleichung der Tangente an den Graphen von  an der Stelle
an der Stelle 
(3 BE)
b)
Weise nach, dass am Graphen von  keine Tangenten mit negativem Anstieg existieren.
keine Tangenten mit negativem Anstieg existieren.
(2 BE)
4
Gegeben ist die Funktion  mit
mit 

Die Abbildung zeigt einen Teil des Graphen von sowie dessen Hochpunkt
sowie dessen Hochpunkt 
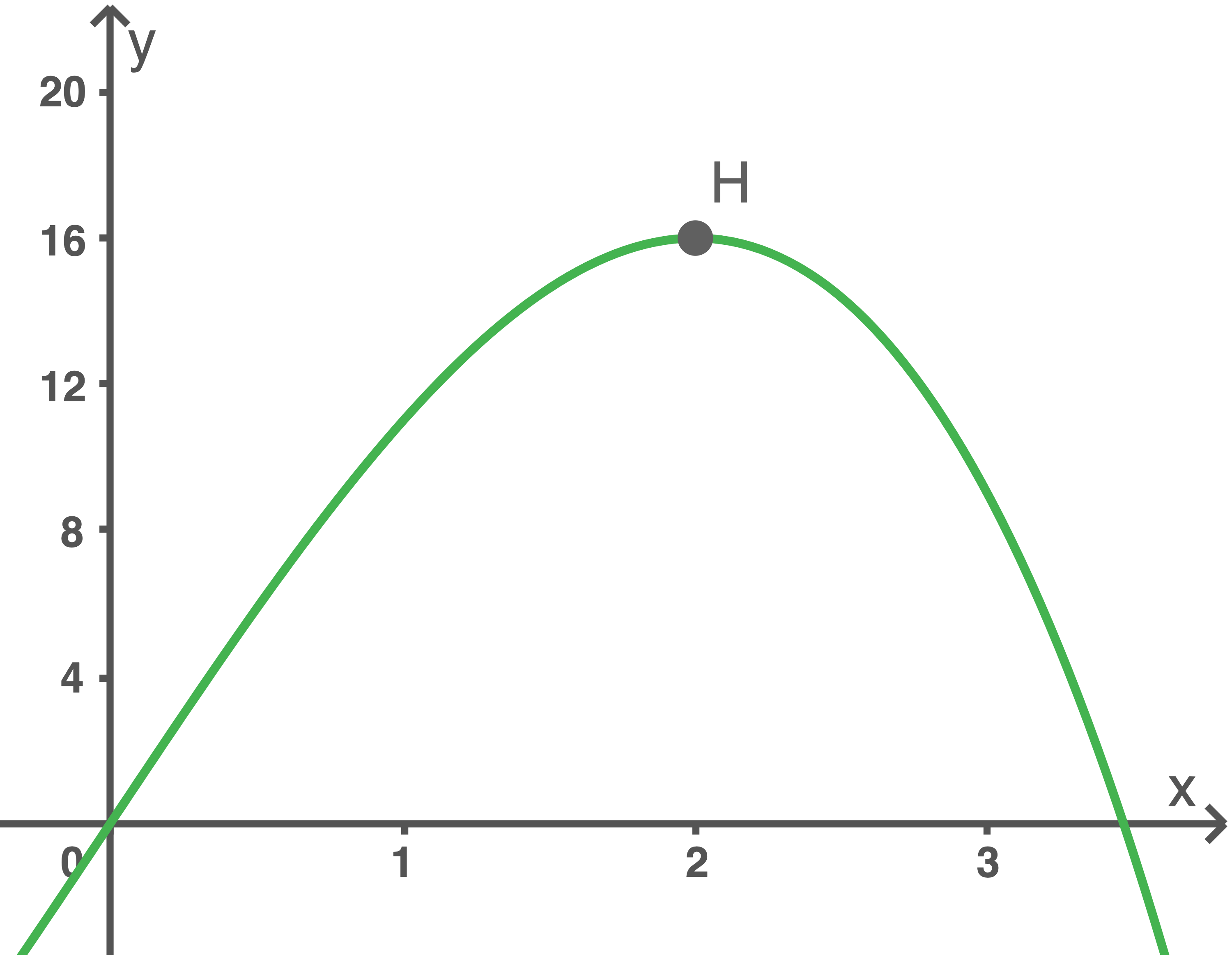
Die Abbildung zeigt einen Teil des Graphen von
a)
Der Graph von  , die
, die  -Achse und die Gerade der Gleichung
-Achse und die Gerade der Gleichung  schließen für
schließen für  eine Fläche ein.
eine Fläche ein.
Zeige, dass diese Fläche den Inhalt besitzt.
besitzt.
Zeige, dass diese Fläche den Inhalt
(2 BE)
b)
Die Gerade  verläuft durch den Punkt
verläuft durch den Punkt  und besitzt eine negative Steigung. Der Graph von
und besitzt eine negative Steigung. Der Graph von  die
die  -Achse und die Gerade
-Achse und die Gerade  schließen für
schließen für  eine Fläche mit dem Inhalt
eine Fläche mit dem Inhalt  ein.
ein.
Bestimme die Koordinaten des Schnittpunkts der Gerade mit der
mit der  -Achse.
-Achse.
Bestimme die Koordinaten des Schnittpunkts der Gerade
(3 BE)

5
Das Dreieck  mit den Punkten
mit den Punkten 
 und
und  ist im Punkt
ist im Punkt  rechtwinklig und liegt in der Ebene mit der Gleichung
rechtwinklig und liegt in der Ebene mit der Gleichung 
a)
Weise nach, dass das Dreieck  den Flächeninhalt
den Flächeninhalt  besitzt.
besitzt.
(2 BE)
b)
Bestimme die Koordinaten eines Punkts  so, dass das Volumen der Pyramide
so, dass das Volumen der Pyramide  gleich
gleich  ist.
ist.
(3 BE)
6
Gegeben sind die Punkte  und
und  Das Quadrat
Das Quadrat  der Seite
der Seite  liegt parallel zur
liegt parallel zur  -Ebene.
-Ebene.
a)
Berechne den Flächeninhalt des Quadrats 
(2 BE)
b)
Ermittle die Koordinaten eines weiteren Eckpunkts des Quadrats.
(3 BE)
7
Jedes Überraschungsei eines Herstellers enthält entweder eine Figur oder keine Figur, wobei der Anteil der Überraschungseier mit einer Figur  beträgt.
beträgt.
a)
Zehn Überraschungseier werden nacheinander zufällig ausgewählt.
Gib einen Term zur Berechnung der Wahrscheinlichkeit dafür an, dass nur in den letzten beiden Überraschungseiern jeweils eine Figur enthalten ist.
Gib einen Term zur Berechnung der Wahrscheinlichkeit dafür an, dass nur in den letzten beiden Überraschungseiern jeweils eine Figur enthalten ist.
(2 BE)
b)
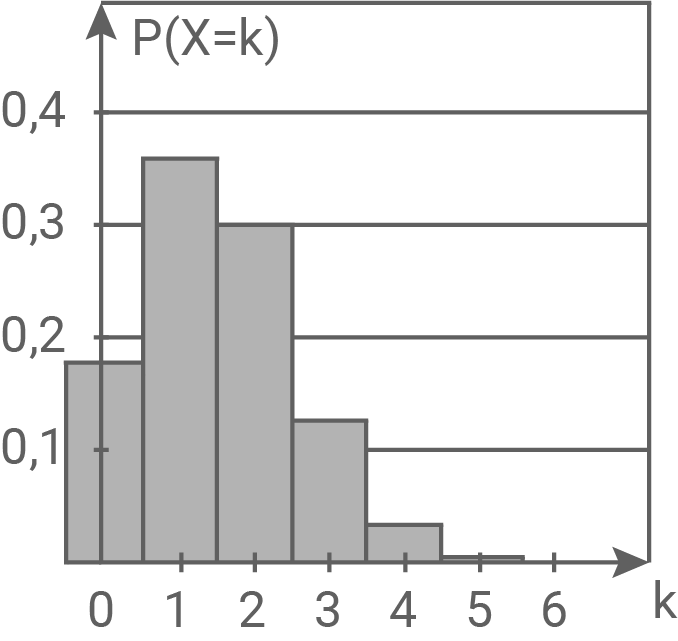
Sechs Überraschungseier werden zufällig ausgewählt. Die Zufallsgröße  gibt an, wie viele dieser Überraschungseier eine Figur enthalten. Eine der folgenden Abbildungen stellt die Wahrscheinlichkeitsverteilung dieser Zufallsgröße
gibt an, wie viele dieser Überraschungseier eine Figur enthalten. Eine der folgenden Abbildungen stellt die Wahrscheinlichkeitsverteilung dieser Zufallsgröße  dar:
dar:
Kreuze diese an.
Begründe, dass die beiden anderen Abbildungen dies nicht sind.
|
|
|
|||
Begründe, dass die beiden anderen Abbildungen dies nicht sind.
(3 BE)
8
Lena wird ein Glücksspiel mit zwei Würfeln angeboten. Bevor sie spielt, berechnet sie den Erwartungswert für ihren Gewinn:
a)
Beschreibe die Bedeutung dieses berechneten Werts im Sachzusammenhang.
(2 BE)
b)
Beschreibe ein zur Rechnung passendes Spiel mit den zugehörigen Gewinnregeln.
(3 BE)
1.
a)
Nullstellen bestimmen
![\(\begin{array}[t]{rll}
f(x)&=&0 \\[5pt]
(3+x)\cdot(4-x)&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/854509bf83776c579fd7d65efe6f0765ad2ded4addf12be551bdefe3d41bf9a2_light.svg) Mit dem Satz des Nullprodukts folgt
Mit dem Satz des Nullprodukts folgt  und
und  Polstellen bestimmen
Polstellen sind die Werte von
Polstellen bestimmen
Polstellen sind die Werte von  für die der Nenner der Funktion
für die der Nenner der Funktion  Null wird:
Null wird:
![\(\begin{array}[t]{rll}
x^2-9&=&0 &\quad \scriptsize \mid\; +9\\[5pt]
x^2&=&9 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
x_1&= -3 \\[5pt]
x_2&= 3
\end{array}\)](https://www.schullv.de/resources/formulas/67b32869959b7e3361ba17c352f8d4d611d35e0345c4ba24bcf26eef69496cc8_light.svg) Lösung der Gleichung
Lösung der Gleichung  bestimmen
Es gilt
bestimmen
Es gilt  Es folgt:
Es folgt:
![\(\begin{array}[t]{rll}
x+2&=& 0&\quad \scriptsize \mid\; -2\\[5pt]
x&=&-2
\end{array}\)](https://www.schullv.de/resources/formulas/f19b4fb04c44a0fc53c513acae0299ed375ae25fea90bf15092ce5a27f34ae84_light.svg) Somit ist
Somit ist  die Lösung der Gleichung.
die Lösung der Gleichung.
b)
2.
3.
a)
Ableiten von  liefert:
liefert:
 Für die Steigung
Für die Steigung  der Tangente
der Tangente  folgt damit:
folgt damit:
![\(\begin{array}[t]{rll}
m&=& f](https://www.schullv.de/resources/formulas/eb30170b0f9453b2b9815b5840a61bd3ccfc41600d9de3d9dba0c9ebe8221f45_light.svg) An der Stelle
An der Stelle  gilt für den Funktionswert von
gilt für den Funktionswert von 
 Einsetzen des Punktes
Einsetzen des Punktes  in die Tangentengleichung liefert:
in die Tangentengleichung liefert:
![\(\begin{array}[t]{rll}
1&=&\dfrac{3}{2} \cdot 0 +b \\[5pt]
1&=&b
\end{array}\)](https://www.schullv.de/resources/formulas/d30d00863c3072a14aef319fc1d041b3f24a5294ca80e10508dabf7966a81378_light.svg) Die Gleichung der Tangente an den Graphen von
Die Gleichung der Tangente an den Graphen von  im Punkt
im Punkt  lautet somit
lautet somit 
b)
Wenn die Funktion  die die Steigung von
die die Steigung von  angibt, für beliebiges
angibt, für beliebiges  größer als Null ist, existieren keine Tangenten mit negativer Steigung. Da stets
größer als Null ist, existieren keine Tangenten mit negativer Steigung. Da stets  gilt, ist das erfüllt.
gilt, ist das erfüllt.
4
a)
Da die betrachtete Fläche vollständig oberhalb der  -Achse liegt, ergibt sich der gesuchte Flächeninhalt wie folgt:
-Achse liegt, ergibt sich der gesuchte Flächeninhalt wie folgt:
b)
Die Gerade  schneidet die
schneidet die  -Achse in einem Punkt
-Achse in einem Punkt  und verläuft durch den Punkt
und verläuft durch den Punkt  Für die Steigung von
Für die Steigung von  folgt damit:
folgt damit:
 Da
Da  den
den  -Achsenabschnitt angibt, gilt
-Achsenabschnitt angibt, gilt  Die Gleichung der Geraden in Abhängigkeit von
Die Gleichung der Geraden in Abhängigkeit von  lautet daher:
lautet daher:
 Mit dem Integral über die Differenzenfunktion
Mit dem Integral über die Differenzenfunktion  folgt:
Die Gerade
folgt:
Die Gerade  schneidet die
schneidet die  -Achse somit im Punkt
-Achse somit im Punkt 
5
a)
b)
Mit  als Grundfläche der Pryamide gilt nach Teilaufgabe a) direkt
als Grundfläche der Pryamide gilt nach Teilaufgabe a) direkt  Somit folgt:
Somit folgt:
![\(\begin{array}[t]{rll}
V&=&\dfrac{1}{3}\cdot A_G\cdot h \\[5pt]
25&=&\dfrac{1}{3}\cdot \dfrac{25}{2} \cdot h \\[5pt]
6&=&h
\end{array}\)](https://www.schullv.de/resources/formulas/e824cc2437ce3a3927e7e7ad25a0f2936c31cfa9c482990c21fb9298872298d0_light.svg) Die Höhe
Die Höhe  entspricht dem Abstand von
entspricht dem Abstand von  zur Ebene, in der die Grundfläche liegt. Diese besitzt die Gleichung
zur Ebene, in der die Grundfläche liegt. Diese besitzt die Gleichung  somit haben alle Punkte mit einer
somit haben alle Punkte mit einer  -Koordinate von
-Koordinate von  und
und  einen Abstand von
einen Abstand von  zu dieser Ebene.
zu dieser Ebene.
Ein Punkt der diese Bedingung erfüllt ist beispielsweise
Ein Punkt der diese Bedingung erfüllt ist beispielsweise
6.
a)
b)
Durch Vertauschen der  - und
- und  -Koordinate von
-Koordinate von  und Veränderung des Vorzeichens bei einer der beiden, wird ein Vektor erhalten, der senkrecht auf
und Veränderung des Vorzeichens bei einer der beiden, wird ein Vektor erhalten, der senkrecht auf  steht und den gleichen Betrag besitzt:
steht und den gleichen Betrag besitzt:
 Somit ergibt sich:
Somit ergibt sich:

 Ein weiterer Eckpunkt ist somit zum Beispiel gegeben durch
Ein weiterer Eckpunkt ist somit zum Beispiel gegeben durch 
7.
a)
Mit der Pfadmultiplikationsregel folgt für die gesuchte Wahrscheinlichkeit 

b)
Da  aller Überraschungseier unabhängig von einander eine Figur enthalten oder nicht, ist die Wahrscheinlichkeit dafür eine Figur zu enthalten bei jedem Überraschungsei gleich und
aller Überraschungseier unabhängig von einander eine Figur enthalten oder nicht, ist die Wahrscheinlichkeit dafür eine Figur zu enthalten bei jedem Überraschungsei gleich und  kann als binomialverteilt mit den Parametern
kann als binomialverteilt mit den Parametern  und
und  angenommen werden. Der Erwartungswert von
angenommen werden. Der Erwartungswert von  beträgt somit
beträgt somit 
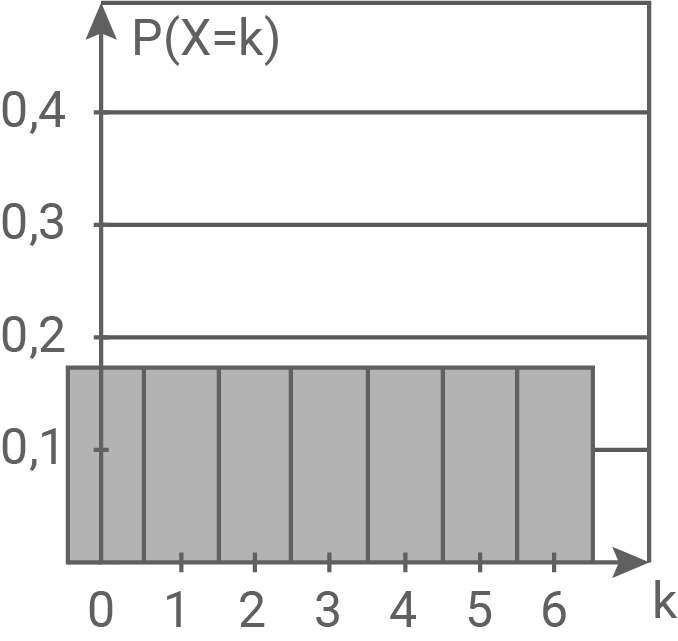
 Das zweite Diagramm stellt eine Gleichverteilung dar. Da
Das zweite Diagramm stellt eine Gleichverteilung dar. Da  binomialverteilt ist, kann diese Abbildung nicht die gesuchte sein.
binomialverteilt ist, kann diese Abbildung nicht die gesuchte sein.
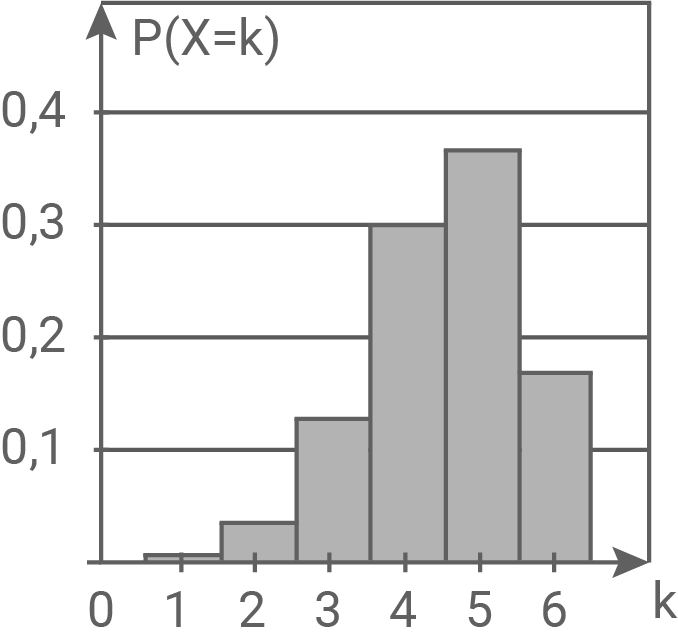
Die beiden höchsten Balken im dritten Diagramm befinden sich bei und
und  nicht bei
nicht bei  und
und  nahe dem Erwartungswert der Zufallsgröße. Abbildung 3 kann somit ebenfalls nicht die gesuchte sein.
nahe dem Erwartungswert der Zufallsgröße. Abbildung 3 kann somit ebenfalls nicht die gesuchte sein.
Damit stellt das erste Diagramm die Wahrscheinlichkeitsverteilung der Zufallsgröße dar.
dar.
Die beiden höchsten Balken im dritten Diagramm befinden sich bei
Damit stellt das erste Diagramm die Wahrscheinlichkeitsverteilung der Zufallsgröße
8.
a)
Der errechnete Erwartungswert zeigt, dass Lena auf lange Sicht einen durschnittlichen Verlust von  pro Spiel macht.
pro Spiel macht.
b)
Es wird mit zwei Würfeln geworfen, die mit den Zahlen von  bis
bis  beschriftet sind. Der Spieleinsatz bei dem Spiel beträgt
beschriftet sind. Der Spieleinsatz bei dem Spiel beträgt  Euro, die Gewinnauszahlung
Euro, die Gewinnauszahlung  Euro. Der Gewinn wird ausgezahlt, wenn zwei gleiche Zahlen gewürfelt werden, dafür beträgt die Wahrscheinlichkeit
Euro. Der Gewinn wird ausgezahlt, wenn zwei gleiche Zahlen gewürfelt werden, dafür beträgt die Wahrscheinlichkeit  Werden zwei unterschiedliche Zahlen gewürfelt, verfällt der Einsatz.
Werden zwei unterschiedliche Zahlen gewürfelt, verfällt der Einsatz.