Teil C2

In einer Zeitschrift wurde veröffentlicht, dass in Thüringen $36,30\;\%$ der Prüflinge die Führerscheinprüfung nicht bestehen.
Nach: www.autobild.de (16.11.2016)

In Thüringen melden sich 50 Teilnehmer eines Fahrschulkurses zur Prüfung an.
Die binomialverteilte Zufallsgröße $X$ beschreibt die Anzahl der Prüfungsteilnehmer, die die Prüfung voraussichtlich nicht bestehen werden.

Berechne die Wahrscheinlichkeit folgender Ereignisse:

$A:\,=$

„Genau 30 Teilnehmer werden die Prüfung voraussichtlich bestehen.“

$B:\,=$

„Mindestens 30 Teilnehmer werden die Prüfung voraussichtlich bestehen.“

(4 BE)

Die Anzahl der Teilnehmer, die die Prüfung nicht bestehen, weicht höchstens um die Standardabweichung vom Erwartungswert ab.
Ermittle die zugehörige Wahrscheinlichkeit.

(4 BE)

Die Inhaberin einer Fahrschule ist sich sicher, dass die Durchfallquote ihrer Fahrschule niedriger als $p_0=36,30\;\%$ $(H_0)$ ist. Dazu überprüft sie die Ergebnisse der letzten 100 Prüflinge. Sind darunter höchstens 30 Teilnehmer, die die Prüfung nicht bestanden haben, will sie davon ausgehen, dass in ihrer Fahrschule die Durchfallquote niedriger ist $(H_1:p_1\lt 36,30\;\%).$

Berechne den Fehler 1. Art. Beschreibe die Bedeutung des Fehlers im Sachzusammenhang.

(3 BE)

Berechne den Fehler 2. Art für den Fall $p_1=25\;\%.$
Untersuche die Entwicklung des Fehlers, wenn sich der Wert von $p_1$ dem Wert $p_0$ nähert.

(4 BE)

Formuliere eine neue Entscheidungsregel so, dass der Fehler 1. Art höchstens $5\;\%$ beträgt.

(4 BE)

Es wird angenommen, dass die vom Teilnehmer benötigte Prüfungszeit normalverteilt mit dem Erwartungswert $\mu=45$ Minuten und der Standardabweichung $\sigma=5$ Minuten ist.

Dargestellt ist der Graph der entsprechenden Dichtefunktion.

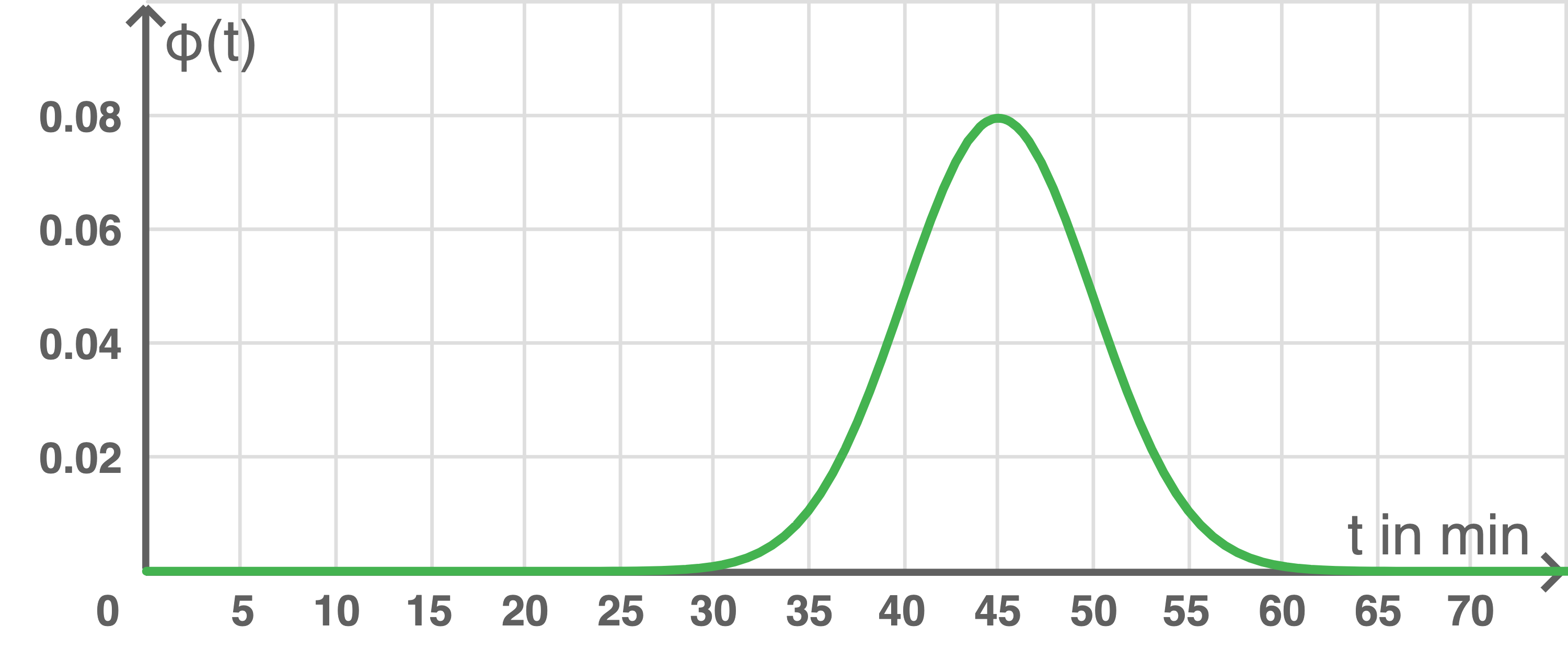thüringen mathe abi 2017 teil c2 abbildung 1

Der Flächeninhalt unter dem Graphen der Funktion für $t\leq40$ Minuten beträgt etwa $0,16$ Flächeneinheiten.
Interpretiere diesen Wert im Sachzusammenhang.

(2 BE)

Berechne die Wahrscheinlichkeit folgender Ereignisse:

$C:\,=$

„Ein zufällig ausgewählter Prüfling benötigt genau 45 Minuten“

$D:\,=$

„Ein zufällig ausgewählter Prüfling benötigt höchstens 35 Minuten“

(4 BE)

In einem kartesischen Koordinatensystem sind die Punkte $L(-1\mid 0\mid 3)$ und $M_k(k\mid k\mid k)$ mit $k\in\mathbb{R}$ gegeben. Alle Punkte $M_k$ liegen auf einer Geraden $g$ .

Ermittle alle Werte von $k$ so, dass der Abstand der Punkte $L$ und $M_k$ $5$ Längeneinheiten beträgt.

(3 BE)

Bestimme $k$ so, dass $L$ und $M_k$ den minimalen Abstand besitzen.
Gib diesen Abstand an.

(5 BE)

Berechne die Größe des Schnittwinkels von $g$ mit der $xy$ -Ebene.

(3 BE)

Der Punkt $L$ wird an der Gerade $g$ gespiegelt. Ermittle die Koordinaten des Bildpunktes $\(L$

(4 BE)

Die Zufallsvariable $X,$ die die Anzahl der Prüfungsteilnehmer beschreibt, die die Prüfung nicht bestehen, ist binomialverteilt mit den Parametern $n=50$ und $p=0,363.$ Die Zufallsvariable $Y$ beschreibt die Anzahl der Prüfungsteilnehmer, die die Prüfung bestehen und ist somit binomialverteilt mit den Parametern $n=50$ und $p=0,637.$ Mit dem CAS folgt:

$\begin{array}[t]{rll} P(A)&=&B_{50;0,637}(Y=30) \\[5pt] &\approx& 0,0990 \\[5pt] &=& 9,9\,\% \end{array}$

$\begin{array}[t]{rll} P(B)&=&B_{50;0,637}(Y\geq 30) \\[5pt] &\approx& 0,7573 \\[5pt] &=& 75,73\,\% \end{array}$

Mathematische Berechnungen mit binomialen Wahrscheinlichkeiten in einem Dokument.

Für den Erwartungswert $\mu$ und die Standardabweichung $\sigma$ der Zufallsgröße $X$ gilt:

$\mu=n\cdot p = 0,363\cdot 50$ $= 18,15$

$\sigma=\sqrt{n \cdot p \cdot (1-p)}$ $= \sqrt{50 \cdot 0,363 \cdot 0,637}\approx 3,4$

Die Grenzen des gesuchten Intervalls ergeben sich als $18,15-3,4 = 14,75$ und $18,15+3,4 = 21,55.$ Da die Zufallsgröße $X$ nur ganze Werte annimmt, folgt das Intervall $[15;21].$ Das CAS liefert:

$B_{50;0,363}(15\leq X \leq 21 )$ $\approx 0,6969 =69,69\,\%$

Die gesuchte Wahrscheinlichkeit beträgt somit ca. $69,69\,\%.$

Alternativer Lösungsweg

Da die Laplacebedingung $\sigma\approx3,4\gt3$ erfüllt ist, folgt mit der Sigma-Regel für die einfache Sigma-Umgebung, dass ca. $68,3\,\%$ der Werte von $X$ im betrachteten Intervall $[\mu-\sigma;\mu+\sigma]$ liegen.

Fehler 1. Art berechnen

Die Zufallsvariable $Z$ beschreibt die Anzahl der Prüfungsteilnehmer, die die Prüfung nicht bestehen und ist binomialverteilt mit den Parametern $n=100$ und $p=p_0=0,363.$ Der Verwerfungsbereich ist gegeben als $V=\{0;1;\ldots;30\}.$ Mit dem CAS folgt somit für den Fehler 1. Art $\alpha:$

$\begin{array}[t]{rll} \alpha&=&B_{100;0,363}(Z\leq 30) \\[5pt] &\approx& 0,1129 \\[5pt] &=& 11,29\,\% \end{array}$

Sachzusammenhang erklären

Im Sachzusammenhang wird der Fehler 1. Art begangen, wenn die Inhaberin der Fahrschule irrtümlich davon ausgeht, dass die Durchfallquote in ihrer Fahrschule geringer als insgesamt in Thüringen ist, obwohl sie dort tatsächlich genauso hoch ist.

Die Zufallsvariable $Z_1$ beschreibt die Anzahl der Prüfungsteilnehmer, die die Prüfung nicht bestehen und ist binomialverteilt mit den Parametern $n=100$ und $p=p_1=0,25.$ Der Fehler 2. Art sagt aus, dass die Nullhypothese fälschlicherweise bestätigt wird, obwohl die Alternativhypothese korrekt ist. Mit dem CAS folgt somit für den Fehler 2. Art $\beta:$

$\begin{array}[t]{rll} \beta&=&1-B_{100;0,25}(Z\leq30) \\[5pt] &\approx& 0,1038 \end{array}$

Systematisches Ausprobieren durch Einsetzen verschiedener Werte für $p_1$ in den CAS zeigt, dass der Fehler 2. Art umso größer wird, je mehr $p_1$ sich von unten an $p_0$ annähert.

Der neue Verwerfungsbereich $V=\{0;\ldots;k\}$ muss so gewählt werden, dass gilt:

$B_{100;0,363}(Z\leq k)\leq 0,05=5\,\%$

Systematisches Ausprobieren im CAS liefert:

$B_{100;0,363}(Z\leq 27)$ $\approx 0,0316 = 3,16\,\%$

$B_{100;0,363}(Z\leq 28)$ $\approx 0,0504 = 5,04\,\%$

Es folgt $k=27$ und damit der neue Verwerfungsbereich $V=\{0;\ldots;27\}.$

Der Wert $\phi(t)$ gibt die Wahrscheinlichkeit dafür an, dass ein Teilnehmer genau $t$ Minuten für die Prüfung benötigt. Dass der Flächeninhalt unter dem Graphen von $\phi$ für $t\leq 40$ etwa $0,16\;\text{FE}$ beträgt, sagt somit aus, dass ca. $16\,\%$ der Teilnehmer die Prüfung nach spätestens $40$ Minuten abgeben.

Die Zufallsvariable $Z_2$ gibt die Zeit in Minuten an, die ein ausgewählter Prüfling insgesamt für die Prüfung benötigt und ist normalverteilt mit $\mu=45$ und $\sigma=5.$ Mit dem CAS folgt:

$\begin{array}[t]{rll} P(C)&=&P(Z_2=45) \\[5pt] &\approx& 0,0798 \\[5pt] &=&7,98\,\% \end{array}$

$\begin{array}[t]{rll} P(D)&=&P(Z_2\leq 35) \\[5pt] &\approx& 0,0228 \\[5pt] &=&2,28\,\% \end{array}$

Dialogfenster für Normalverteilung mit Eingabefeldern für X-Wert, μ und σ.

Screenshot einer Software mit Berechnungen für normPdf und normCdf.

$\begin{array}[t]{rll} \overline{LM_k}&=& 5 \\[5pt] \left\vert \pmatrix{k- (-1)\\k-0\\k-3}\right\vert&=& 5 \\[5pt] \end{array}$

Mit dem solve-Befehl des CAS folgt:

$\begin{array}[t]{rll} k_1&=&-\dfrac{5}{3} \\[5pt] k_2&=&3 \end{array}$

Mathematische Gleichung zur Lösung eines Problems mit Variablen.

Für und $k_1=-\dfrac{5}{3}$ und $k_2=3$ haben die Punkte $L$ und $M_k$ somit einen Abstand von $5\;\text{LE}.$

Der Abstand zwischen den Punkten kann, abhängig von $k,$ durch die folgende Funktion dargestellt werden:

$f(k)=\left\vert\overline{LM_k}\right\vert$ $=\sqrt{3k^2-4k+10}$

1. Schritt: Notwendiges Kriterium für Extremstellen anwenden

Für die ersten beiden Ableitungen folgt mit dem CAS:

$\(f$

Mit dem solve-Befehl des CAS liefert $\(f$

$\begin{array}[t]{rll} k&=& \dfrac{2}{3} \end{array}$

Mathematische Berechnungen und Gleichungen in einem Dokument.

2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen

$\(f$

An der Stelle $k=\frac{2}{3}$ besitzt $f$ somit ein lokales Minimum. Mit dem CAS folgt für den minimalen Abstand der Punkte $L$ und $M_k$ somit:

$f\left(\dfrac{2}{3}\right)\approx 2,94\;\text{LE}$

Screenshot eines mathematischen Programms mit Gleichungen und Ergebnissen.

Die Punktmenge $M_k$ liegt auf einer Geraden $g.$ Als mögliche Geradengleichung ergibt sich:

$g:\overrightarrow{x}=\pmatrix{k\\k\\k}$ $=\pmatrix{0\\0\\0}+k\cdot \pmatrix{1\\1\\1}$

Ein Normalenvektor der $xy$ -Ebene ist wie folgt gegeben:

$\overrightarrow{n}=\pmatrix{0\\0\\1}$

Mit der Formel für den Schnittwinkel einer Gerade mit einer Ebene liefert der CAS:

$\begin{array}[t]{rll} \sin(\alpha)&=&\dfrac{\left|\pmatrix{0\\0\\1} \circ\pmatrix{1\\1\\1}\right|}{\left|\pmatrix{0\\0\\1}\right|\cdot \left|\pmatrix{1\\1\\1}\right|} \\[5pt] \sin(\alpha)&=&\dfrac{1}{ \sqrt{3}} \\[5pt] \alpha&\approx& 35,26^\circ; \end{array}$

Der Schnittwinkel von $g$ mit der $xy$ -Ebene beträgt somit ca. $35,26^\circ.$

Der Lotfußpunkt $F$ von $L$ bezüglich der Geraden $g$ ist der Punkt auf $g,$ der den geringsten Abstand zu $L$ besitzt. Mit Aufgabenteil b) folgt somit:

$\overrightarrow{OF} = \pmatrix{0\\0\\0}+\dfrac{2}{3}\cdot \pmatrix{1\\1\\1}$ $= \pmatrix{\frac{2}{3}\\\frac{2}{3}\\\frac{2}{3}}$

Für den Ortsvektor des gesuchten Bildpunkts $\(L$ folgt nun:

Rechenweg anzeigen

$\( OL$

Die Koordinaten des Bildpunktes sind somit gegeben durch $\(L$

$\begin{array}[t]{rll} P(A)&=&B_{50;0,637}(Y=30) \\[5pt] &\approx& 0,0990 \\[5pt] &=& 9,9\,\% \end{array}$

$\begin{array}[t]{rll} P(B)&=&B_{50;0,637}(Y\geq 30) \\[5pt] &\approx& 0,7573 \\[5pt] &=& 75,73\,\% \end{array}$

Screenshot einer mathematischen Berechnung mit binomialPDF-Funktion und Ergebnis.

Screenshot einer Software mit einer Berechnung zur binomialen kumulativen Verteilungsfunktion.

Für den Erwartungswert $\mu$ und die Standardabweichung $\sigma$ der Zufallsgröße $X$ gilt:

$\mu=n\cdot p = 0,363\cdot 50$ $= 18,15$

$\sigma=\sqrt{n \cdot p \cdot (1-p)}$ $= \sqrt{50 \cdot 0,363 \cdot 0,637}\approx 3,4$

Die Grenzen des gesuchten Intervalls ergeben sich als $18,15-3,4 = 14,75$ und $18,15+3,4 = 21,55.$ Da die Zufallsgröße $X$ nur ganze Werte annimmt, folgt das Intervall $[15;21].$ Das CAS liefert:

$B_{50;0,363}(15\leq X \leq 21 )$ $\approx 0,6969 =69,69\,\%$

Die gesuchte Wahrscheinlichkeit beträgt somit ca. $69,69\,\%.$

Alternativer Lösungsweg

Fehler 1. Art berechnen

$\begin{array}[t]{rll} \alpha&=&B_{100;0,363}(Z\leq 30) \\[5pt] &\approx& 0,1129 \\[5pt] &=& 11,29\,\% \end{array}$

Sachzusammenhang erklären

$\begin{array}[t]{rll} \beta&=&1-B_{100;0,25}(Z\leq30) \\[5pt] &\approx& 0,1038 \end{array}$

Systematisches Ausprobieren durch Einsetzen verschiedener Werte für $p_1$ in den CAS zeigt, dass der Fehler 2. Art umso größer wird, je mehr $p_1$ sich von unten an $p_0$ annähert.

Der neue Verwerfungsbereich $V=\{0;\ldots;k\}$ muss so gewählt werden, dass gilt:

$B_{100;0,363}(Z\leq k)\leq 0,05=5\,\%$

Systematisches Ausprobieren im CAS liefert:

$B_{100;0,363}(Z\leq 27)$ $\approx 0,0316 = 3,16\,\%$

$B_{100;0,363}(Z\leq 28)$ $\approx 0,0504 = 5,04\,\%$

Es folgt $k=27$ und damit der neue Verwerfungsbereich $V=\{0;\ldots;27\}.$

Die Zufallsvariable $Z_2$ gibt die Zeit in Minuten an, die ein ausgewählter Prüfling insgesamt für die Prüfung benötigt und ist normalverteilt mit $\mu=45$ und $\sigma=5.$ Mit dem CAS folgt:

$\begin{array}[t]{rll} P(C)&=&P(Z_2=45) \\[5pt] &\approx& 0,0798 \\[5pt] &=&7,98\,\% \end{array}$

$\begin{array}[t]{rll} P(D)&=&P(Z_2\leq 35) \\[5pt] &\approx& 0,0228 \\[5pt] &=&2,28\,\% \end{array}$

Mathematische Berechnung mit normCDF-Funktion, die einen Wert von 0.0797 anzeigt.

Screenshot einer Berechnung mit der Funktion normCDF in einem mathematischen Programm.

$\begin{array}[t]{rll} \overline{LM_k}&=& 5 \\[5pt] \left\vert \pmatrix{k- (-1)\\k-0\\k-3}\right\vert&=& 5 \\[5pt] \end{array}$

Mit dem solve-Befehl des CAS folgt:

$\begin{array}[t]{rll} k_1&=&-\dfrac{5}{3} \\[5pt] k_2&=&3 \end{array}$

Mathematische Berechnung mit einer Gleichung und Lösungsansätzen für k in einem Programm.

Für und $k_1=-\dfrac{5}{3}$ und $k_2=3$ haben die Punkte $L$ und $M_k$ somit einen Abstand von $5\;\text{LE}.$

Der Abstand zwischen den Punkten kann, abhängig von $k,$ durch die folgende Funktion dargestellt werden:

$f(k)=\left\vert\overline{LM_k}\right\vert$ $=\sqrt{3k^2-4k+10}$

1. Schritt: Notwendiges Kriterium für Extremstellen anwenden

Für die ersten beiden Ableitungen folgt mit dem CAS:

$\(f$

Mit dem solve-Befehl des CAS liefert $\(f$

$\begin{array}[t]{rll} k&=& \dfrac{2}{3} \end{array}$

2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen

$\(f$

Screenshot einer mathematischen Software mit Berechnungen und Funktionen.

An der Stelle $k=\frac{2}{3}$ besitzt $f$ somit ein lokales Minimum. Mit dem CAS folgt für den minimalen Abstand der Punkte $L$ und $M_k$ somit:

$f\left(\dfrac{2}{3}\right)\approx 2,94\;\text{LE}$

Die Punktmenge $M_k$ liegt auf einer Geraden $g.$ Als mögliche Geradengleichung ergibt sich:

$g:\overrightarrow{x}=\pmatrix{k\\k\\k}$ $=\pmatrix{0\\0\\0}+k\cdot \pmatrix{1\\1\\1}$

Ein Normalenvektor der $xy$ -Ebene ist wie folgt gegeben:

$\overrightarrow{n}=\pmatrix{0\\0\\1}$

Mit der Formel für den Schnittwinkel einer Gerade mit einer Ebene liefert der CAS:

Der Schnittwinkel von $g$ mit der $xy$ -Ebene beträgt somit ca. $35,26^\circ.$

Der Lotfußpunkt $F$ von $L$ bezüglich der Geraden $g$ ist der Punkt auf $g,$ der den geringsten Abstand zu $L$ besitzt. Mit Aufgabenteil b) folgt somit:

$\overrightarrow{OF} = \pmatrix{0\\0\\0}+\dfrac{2}{3}\cdot \pmatrix{1\\1\\1}$ $= \pmatrix{\frac{2}{3}\\\frac{2}{3}\\\frac{2}{3}}$

Für den Ortsvektor des gesuchten Bildpunkts $\(L$ folgt nun:

Rechenweg anzeigen

$\( OL$

Die Koordinaten des Bildpunktes sind somit gegeben durch $\(L$