Teil B1
Gegeben ist die Funktion  mit
mit 

Die Höhenprofillinie längs des Grundstückes kann näherungsweise durch die Funktion im Intervall
im Intervall  beschrieben werden.
beschrieben werden.
Die Werte von und
und  sind Längen in Meter.
sind Längen in Meter.

 eine Funktion
eine Funktion  durch
durch 
 .
.
Jeder zugehörige Graph besitzt zwei Extrempunkte.
a)
Berechne die Koordinaten der lokalen Extrempunkte und des Punktes mit dem größten Anstieg.
(4 BE)
b)
Untersuche, ob auf dem Graphen von  Punkte existieren, die gleichweit von der Geraden
Punkte existieren, die gleichweit von der Geraden  entfernt sind und in denen sich die Anstiege nur durch das Vorzeichen unterscheiden.
entfernt sind und in denen sich die Anstiege nur durch das Vorzeichen unterscheiden.
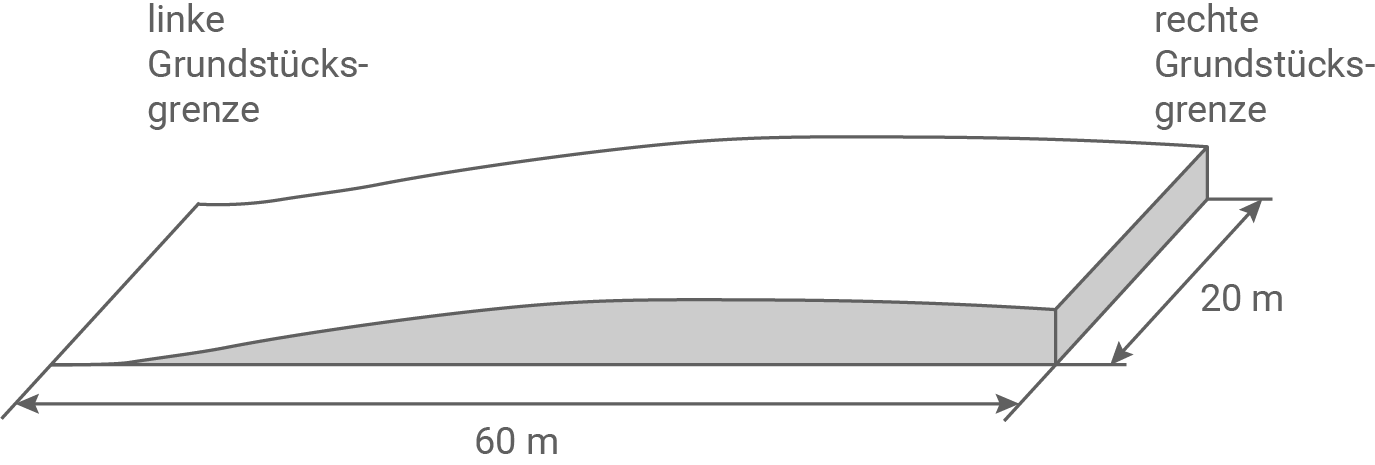
Eine Familie möchte auf ihrem Grundstück ein Wohnhaus errichten. Der Grundriss des Grundstückes ist ein Rechteck.
(2 BE)
Die Höhenprofillinie längs des Grundstückes kann näherungsweise durch die Funktion
Die Werte von

c)
Skizziere die Profillinie in einem Koordinatensystem mit geeignet eingeteilten Achsen.
Gib den größten Anstieg des Geländes in Prozent an.
Das Haus soll auf einer waagerechten Fläche errichtet werden. Dazu soll parallel zur linken Grundstücksgrenze eine Mauer errichtet werden. Ausgehend von der Höhe der rechten Grundstücksgrenze wird das Grundstück planiert. Die abgetragene Erde soll rechts der Mauer aufgefüllt werden, so dass eine waagerechte Fläche vom rechten Grundstücksrand bis zur Mauer entsteht.
Gib den größten Anstieg des Geländes in Prozent an.
(3 BE)
d)
Veranschauliche den Sachverhalt in deiner Skizze aus Aufgabe c).
Berechne die Größe des zu bewegenden Erdvolumens und die Entfernung der Mauer vom linken Grundstücksrand.
Gegeben ist für jede reelle Zahl Berechne die Größe des zu bewegenden Erdvolumens und die Entfernung der Mauer vom linken Grundstücksrand.
(5 BE)
Jeder zugehörige Graph besitzt zwei Extrempunkte.
e)
Begründe ohne Verwendung der Mittel der Differentialgleichung, dass die  -Koordinaten der Extrempunkte unabhängig von
-Koordinaten der Extrempunkte unabhängig von  sind und ein Extrempunkt immer im Ursprung liegt.
sind und ein Extrempunkt immer im Ursprung liegt.
(2 BE)
f)
Gib den Wertebereich von  in Abhängigkeit von
in Abhängigkeit von  an.
an.
(2 BE)
g)
Die Graphen der Funktion  entstehen durch Spiegelung der Graphen von
entstehen durch Spiegelung der Graphen von  an der Geraden
an der Geraden 
Gib eine Gleichung für an.
an.
Gib eine Gleichung für
(2 BE)
a)
Lokale Extrempunkte berechnen
Mit dem CAS folgt für die ersten zwei Ableitungen von 


 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&=&0 \\[5pt]
x_2&=&40
\end{array}\)](https://www.schullv.de/resources/formulas/14a53282bad0a9090d127f2a45f0a82dd66eb026e93cc350dd08d5ac347deb56_light.svg) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von  und
und  in
in  liefert mit dem CAS:
liefert mit dem CAS:

 Der Graph von
Der Graph von  besitzt also bei
besitzt also bei  einen lokalen Tiefpunkt und bei
einen lokalen Tiefpunkt und bei  einen lokalen Hochpunkt.
3. Schritt: Funktionswerte ausrechnen
Einsetzen von
einen lokalen Hochpunkt.
3. Schritt: Funktionswerte ausrechnen
Einsetzen von  und
und  in
in  liefert mit dem CAS:
liefert mit dem CAS:
![\(\begin{array}[t]{rll}
f(0)&=&0 \\[5pt]
f(40)&\approx&3,9
\end{array}\)](https://www.schullv.de/resources/formulas/130622d68011d745f09db6c2e289d5a6ce4623cb4d4d8d9cf5cdc0a58d63d6e1_light.svg) Die Koordinaten der lokalen Extrempunkte von
Die Koordinaten der lokalen Extrempunkte von  sind somit
sind somit  und ca.
und ca.  Punkt mit dem größten Anstieg berechnen
Für die dritte Ableitung von
Punkt mit dem größten Anstieg berechnen
Für die dritte Ableitung von  folgt mit dem CAS:
folgt mit dem CAS:


 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_3&\approx&11,7 \\[5pt]
x_4&\approx&68,3
\end{array}\)](https://www.schullv.de/resources/formulas/e252c7e2ca55c9edb0c0806cb7dcaa55cbe01beb903398de60409c0048bdf30a_light.svg) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von  und
und  in
in  liefert mit dem CAS:
liefert mit dem CAS:


 besitzt also bei
besitzt also bei  einen lokalen Hochpunkt.
3. Schritt: Funktionswert ausrechnen
Einsetzen von
einen lokalen Hochpunkt.
3. Schritt: Funktionswert ausrechnen
Einsetzen von  in
in  liefert mit dem CAS:
liefert mit dem CAS:
![\(\begin{array}[t]{rll}
f(x_3)&\approx&1,38
\end{array}\)](https://www.schullv.de/resources/formulas/a28d6b3c044205215689cca80ff19069e78ba4122b45fcf569944c59717f9612_light.svg) Der Punkt
Der Punkt  mit dem größten Anstieg hat somit ungefähr die Koordinaten
mit dem größten Anstieg hat somit ungefähr die Koordinaten 
b)
Der Hochpunkt  des Graphen von
des Graphen von  liegt auf der Geraden
liegt auf der Geraden  Somit sind die Anstiege bei
Somit sind die Anstiege bei  positiv, und bei
positiv, und bei  negativ. Die gesuchten Punkte sollen gleichweit von der Geraden weg und auf dem Graphen von
negativ. Die gesuchten Punkte sollen gleichweit von der Geraden weg und auf dem Graphen von  liegen und die Anstiege dort sich nur im Vorzeichen unterscheiden, das heißt es soll gelten:
liegen und die Anstiege dort sich nur im Vorzeichen unterscheiden, das heißt es soll gelten:
 mit
mit  Eingabe in den CAS liefert mit Hilfe des solve-Befehls:
Eingabe in den CAS liefert mit Hilfe des solve-Befehls:
![\(\begin{array}[t]{rll}
x_1&=&10^{-38} \\[5pt]
x_2&=&38,3
\end{array}\)](https://www.schullv.de/resources/formulas/f3b4e4650e481ace969afa3263b28fd108faa06c58c3c8c795f8777600864458_light.svg) Die Lösung
Die Lösung  ist annähernd Null und kann somit vernachlässigt werden, da der Hochpunkt selber ausgeschlossen wird. Da
ist annähernd Null und kann somit vernachlässigt werden, da der Hochpunkt selber ausgeschlossen wird. Da  gilt, existieren auf dem Graphen von
gilt, existieren auf dem Graphen von  also Punkte mit den gewünschten Eigenschaften.
also Punkte mit den gewünschten Eigenschaften.
c)
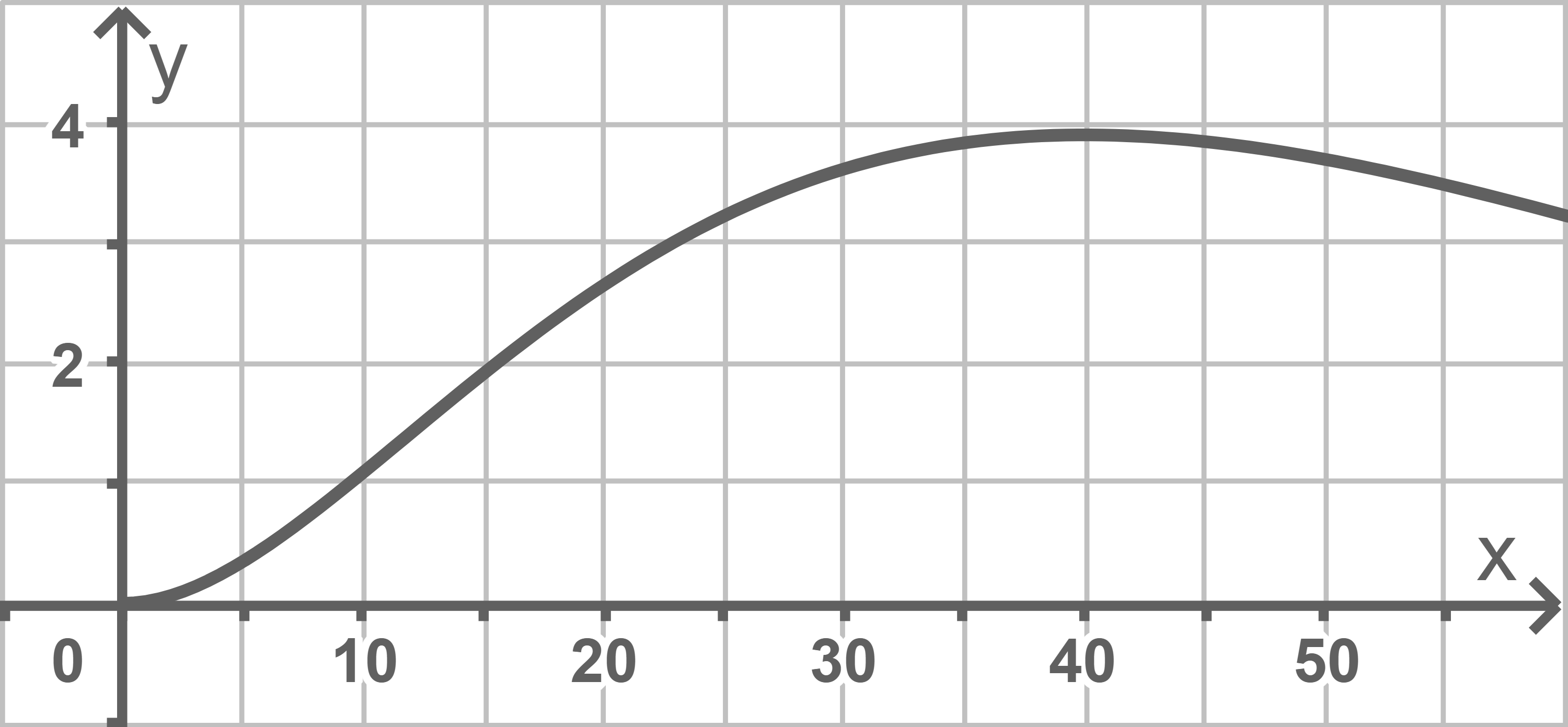
Skizze des Höhenprofils erstellen
Mit Hilfe einer Wertetabelle der Funktionswerte von  im CAS folgt:
im CAS folgt:
 Größten Anstieg des Geländes bestimmen
Die Stelle des größten Anstiegs entspricht der Wendestelle. Mit Aufgabenteil a) folgt somit mit Hilfe des CAS für den größten Anstieg des Geländes:
Größten Anstieg des Geländes bestimmen
Die Stelle des größten Anstiegs entspricht der Wendestelle. Mit Aufgabenteil a) folgt somit mit Hilfe des CAS für den größten Anstieg des Geländes:

d)
Skizze zur Aufgabenstellung erstellen
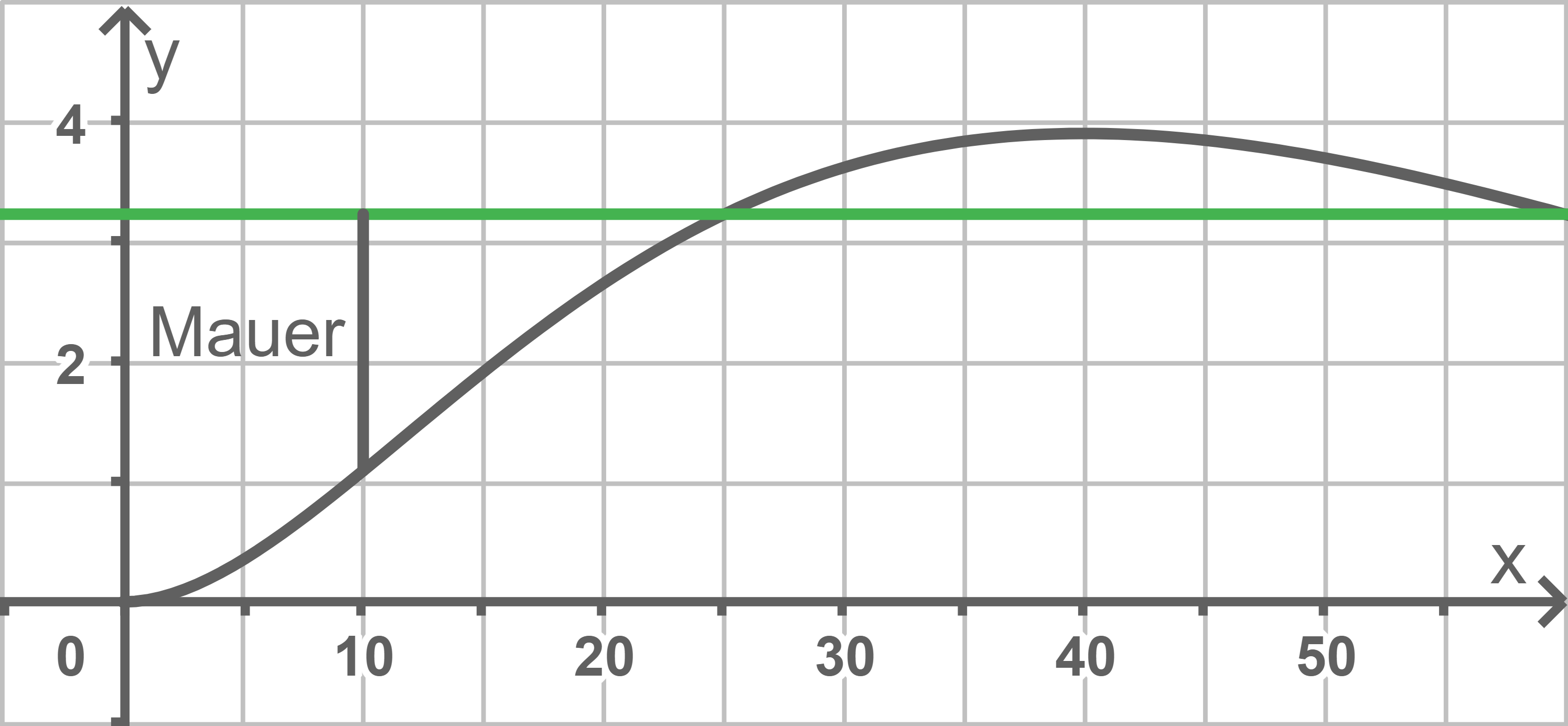 Zu bewegendes Erdvolumen berechnen
Das Volumen der Erde, die bewegt werden soll entspricht dem Inhalt der Fläche, die der Graph von
Zu bewegendes Erdvolumen berechnen
Das Volumen der Erde, die bewegt werden soll entspricht dem Inhalt der Fläche, die der Graph von  im rechten Teil der Skizze mit der Geraden
im rechten Teil der Skizze mit der Geraden  einschließt, multipliziert mit
einschließt, multipliziert mit  Mit dem solve-Befehl des CAS für
Mit dem solve-Befehl des CAS für  ergeben sich die Schnittstellen von
ergeben sich die Schnittstellen von  mit
mit  an denen
an denen  gilt, wie folgt:
gilt, wie folgt:
![\(\begin{array}[t]{rll}
x_1&\approx&25,03 \\[5pt]
x_2&=&60
\end{array}\)](https://www.schullv.de/resources/formulas/c924b64e8ea600fe3a4c7b56f671fc7eacaf818067b06e9b1447bc3b24ed4f9f_light.svg) Mit
Mit  und
und  als Integrationsgrenzen folgt für das Volumen der zu bewegenden Erde mit Hilfe des CAS:
als Integrationsgrenzen folgt für das Volumen der zu bewegenden Erde mit Hilfe des CAS:
![\(\begin{array}[t]{rll}
V&=&20\cdot A \\[5pt]
&=&20\cdot \displaystyle\int_{x_1}^{x_2}(f(x)-g(x))\;\mathrm dx \\[5pt]
&=&20\cdot \displaystyle\int_{25,03}^{60}(f(x)-f(60))\;\mathrm dx \\[5pt]
&\approx&306,46\;[\text{m}^3]
\end{array}\)](https://www.schullv.de/resources/formulas/d1b25c89d1ae620a653748bfe4526817c79098f1dc0794a9ff2616da9d608597_light.svg) Entfernung der Mauer bestimmen
Entfernung der Mauer bestimmen
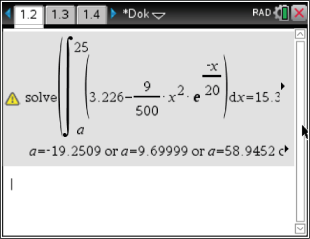

Die Mauer soll an einer Stelle  stehen, sodass gilt:
Mit dem solve-Befehl des CAS folgt eine Lösung, die zwischen
stehen, sodass gilt:
Mit dem solve-Befehl des CAS folgt eine Lösung, die zwischen  und
und  liegt, nämlich
liegt, nämlich  Die Mauer ist somit
Die Mauer ist somit  von der linken Grundstücksgrenze entfernt.
von der linken Grundstücksgrenze entfernt.

e)
Da die Multiplikation mit dem Faktor  eine Streckung oder Stauchung der Funktion in
eine Streckung oder Stauchung der Funktion in  -Richtung oder eine Spiegelung an der
-Richtung oder eine Spiegelung an der  -Achse bewirkt, sind die
-Achse bewirkt, sind die  -Koordinaten aller Extrempunkte unabhängig von
-Koordinaten aller Extrempunkte unabhängig von  Der Faktor
Der Faktor  von
von  ist stets ungleich Null und nach der Aufgabenstellung gilt
ist stets ungleich Null und nach der Aufgabenstellung gilt  Da
Da  gilt, wird
gilt, wird  somit genau dann Null, wenn
somit genau dann Null, wenn  Null wird. Nach Aufgabenteil a) besitzt
Null wird. Nach Aufgabenteil a) besitzt  eine lokale Extremstelle bei
eine lokale Extremstelle bei  damit muss auch
damit muss auch  dort eine lokale Extremstelle besitzen. Ein Extrempunkt der Funktion
dort eine lokale Extremstelle besitzen. Ein Extrempunkt der Funktion  liegt somit immer im Ursprung.
liegt somit immer im Ursprung.
f)
Da  sowie die Exponentialfunktion für alle
sowie die Exponentialfunktion für alle  größer oder gleich Null sind, muss eine Fallunterscheidung durchgeführt werden:
Fall 1:
größer oder gleich Null sind, muss eine Fallunterscheidung durchgeführt werden:
Fall 1: 

 Der Wertebereich von
Der Wertebereich von  für
für  ist somit gegeben durch
ist somit gegeben durch  Fall 2:
Fall 2: 

 Der Wertebereich von
Der Wertebereich von  für
für  ist somit gegeben durch
ist somit gegeben durch 
g)
Die Spiegelung an einer Geraden, die parallel zur  -Achse verläuft, entspricht einer Spiegelung an der
-Achse verläuft, entspricht einer Spiegelung an der  -Achse mit anschließender Verschiebung in
-Achse mit anschließender Verschiebung in  -Richtung. Da die Gerade, an der gespiegelt wird, durch die Gleichung
-Richtung. Da die Gerade, an der gespiegelt wird, durch die Gleichung  gegeben ist, wird zuerst an der
gegeben ist, wird zuerst an der  -Achse gespiegelt und anschließend um
-Achse gespiegelt und anschließend um  Längeneinheiten in
Längeneinheiten in  -Richtung verschoben. Somit folgt:
-Richtung verschoben. Somit folgt:
![\( \begin{array}[t]{rll}
s_{a}(x)&=& -h_a(x)+8 \\[5pt]
&=&- a\cdot x^2 \cdot \mathrm e^{- \frac{1}{20}x} +8
\end{array}\)](https://www.schullv.de/resources/formulas/77ff0f10062e1a05c8a7851b48a7ccd6dd1a73413df367128e5dc70da49f5765_light.svg)
a)
Lokale Extrempunkte berechnen
Mit dem CAS folgt für die ersten zwei Ableitungen von 


 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&=&0 \\[5pt]
x_2&=&40
\end{array}\)](https://www.schullv.de/resources/formulas/14a53282bad0a9090d127f2a45f0a82dd66eb026e93cc350dd08d5ac347deb56_light.svg) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von  und
und  in
in  liefert mit dem CAS:
liefert mit dem CAS:

 Der Graph von
Der Graph von  besitzt also bei
besitzt also bei  einen lokalen Tiefpunkt und bei
einen lokalen Tiefpunkt und bei  einen lokalen Hochpunkt.
3. Schritt: Funktionswerte ausrechnen
Einsetzen von
einen lokalen Hochpunkt.
3. Schritt: Funktionswerte ausrechnen
Einsetzen von  und
und  in
in  liefert mit dem CAS:
liefert mit dem CAS:
![\(\begin{array}[t]{rll}
f(0)&=&0 \\[5pt]
f(40)&\approx&3,9
\end{array}\)](https://www.schullv.de/resources/formulas/130622d68011d745f09db6c2e289d5a6ce4623cb4d4d8d9cf5cdc0a58d63d6e1_light.svg) Die Koordinaten der lokalen Extrempunkte von
Die Koordinaten der lokalen Extrempunkte von  sind somit
sind somit  und ca.
und ca.  Punkt mit dem größten Anstieg berechnen
Für die dritte Ableitung von
Punkt mit dem größten Anstieg berechnen
Für die dritte Ableitung von  folgt mit dem CAS:
folgt mit dem CAS:


 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_3&\approx&11,7 \\[5pt]
x_4&\approx&68,3
\end{array}\)](https://www.schullv.de/resources/formulas/e252c7e2ca55c9edb0c0806cb7dcaa55cbe01beb903398de60409c0048bdf30a_light.svg) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
Einsetzen von  und
und  in
in  liefert mit dem CAS:
liefert mit dem CAS:


 besitzt also bei
besitzt also bei  einen lokalen Hochpunkt.
3. Schritt: Funktionswert ausrechnen
Einsetzen von
einen lokalen Hochpunkt.
3. Schritt: Funktionswert ausrechnen
Einsetzen von  in
in  liefert mit dem CAS:
liefert mit dem CAS:
![\(\begin{array}[t]{rll}
f(x_3)&\approx&1,38
\end{array}\)](https://www.schullv.de/resources/formulas/a28d6b3c044205215689cca80ff19069e78ba4122b45fcf569944c59717f9612_light.svg) Der Punkt
Der Punkt  mit dem größten Anstieg hat somit ungefähr die Koordinaten
mit dem größten Anstieg hat somit ungefähr die Koordinaten 
b)
Der Hochpunkt  des Graphen von
des Graphen von  liegt auf der Geraden
liegt auf der Geraden  Somit sind die Anstiege bei
Somit sind die Anstiege bei  positiv, und bei
positiv, und bei  negativ. Die gesuchten Punkte sollen gleichweit von der Geraden weg und auf dem Graphen von
negativ. Die gesuchten Punkte sollen gleichweit von der Geraden weg und auf dem Graphen von  liegen und die Anstiege dort sich nur im Vorzeichen unterscheiden, das heißt es soll gelten:
liegen und die Anstiege dort sich nur im Vorzeichen unterscheiden, das heißt es soll gelten:
 mit
mit  Eingabe in den CAS liefert mit Hilfe des solve-Befehls:
Eingabe in den CAS liefert mit Hilfe des solve-Befehls:
![\(\begin{array}[t]{rll}
x_1&=&10^{-38} \\[5pt]
x_2&=&38,3
\end{array}\)](https://www.schullv.de/resources/formulas/f3b4e4650e481ace969afa3263b28fd108faa06c58c3c8c795f8777600864458_light.svg) Die Lösung
Die Lösung  ist annähernd Null und kann somit vernachlässigt werden, da der Hochpunkt selber ausgeschlossen wird. Da
ist annähernd Null und kann somit vernachlässigt werden, da der Hochpunkt selber ausgeschlossen wird. Da  gilt, existieren auf dem Graphen von
gilt, existieren auf dem Graphen von  also Punkte mit den gewünschten Eigenschaften.
also Punkte mit den gewünschten Eigenschaften.
c)
Skizze des Höhenprofils erstellen
Mit Hilfe einer Wertetabelle der Funktionswerte von  im CAS folgt:
im CAS folgt:
 Größten Anstieg des Geländes bestimmen
Die Stelle des größten Anstiegs entspricht der Wendestelle. Mit Aufgabenteil a) folgt somit mit Hilfe des CAS für den größten Anstieg des Geländes:
Größten Anstieg des Geländes bestimmen
Die Stelle des größten Anstiegs entspricht der Wendestelle. Mit Aufgabenteil a) folgt somit mit Hilfe des CAS für den größten Anstieg des Geländes:

d)
Skizze zur Aufgabenstellung erstellen
 Zu bewegendes Erdvolumen berechnen
Das Volumen der Erde, die bewegt werden soll entspricht dem Inhalt der Fläche, die der Graph von
Zu bewegendes Erdvolumen berechnen
Das Volumen der Erde, die bewegt werden soll entspricht dem Inhalt der Fläche, die der Graph von  im rechten Teil der Skizze mit der Geraden
im rechten Teil der Skizze mit der Geraden  einschließt, multipliziert mit
einschließt, multipliziert mit  Mit dem solve-Befehl des CAS für
Mit dem solve-Befehl des CAS für  ergeben sich die Schnittstellen von
ergeben sich die Schnittstellen von  mit
mit  an denen
an denen  gilt, wie folgt:
gilt, wie folgt:
![\(\begin{array}[t]{rll}
x_1&\approx&25,03 \\[5pt]
x_2&=&60
\end{array}\)](https://www.schullv.de/resources/formulas/c924b64e8ea600fe3a4c7b56f671fc7eacaf818067b06e9b1447bc3b24ed4f9f_light.svg) Mit
Mit  und
und  als Integrationsgrenzen folgt für das Volumen der zu bewegenden Erde mit Hilfe des CAS:
als Integrationsgrenzen folgt für das Volumen der zu bewegenden Erde mit Hilfe des CAS:
![\(\begin{array}[t]{rll}
V&=&20\cdot A \\[5pt]
&=&20\cdot \displaystyle\int_{x_1}^{x_2}(f(x)-g(x))\;\mathrm dx \\[5pt]
&=&20\cdot \displaystyle\int_{25,03}^{60}(f(x)-f(60))\;\mathrm dx \\[5pt]
&\approx&306,46\;[\text{m}^3]
\end{array}\)](https://www.schullv.de/resources/formulas/d1b25c89d1ae620a653748bfe4526817c79098f1dc0794a9ff2616da9d608597_light.svg) Entfernung der Mauer bestimmen
Die Mauer soll an einer Stelle
Entfernung der Mauer bestimmen
Die Mauer soll an einer Stelle  stehen, sodass gilt:
stehen, sodass gilt:

Mit dem solve-Befehl des CAS folgt eine Lösung, die zwischen  und
und  liegt, nämlich
liegt, nämlich  Die Mauer ist somit
Die Mauer ist somit  von der linken Grundstücksgrenze entfernt.
von der linken Grundstücksgrenze entfernt.
e)
Da die Multiplikation mit dem Faktor  eine Streckung oder Stauchung der Funktion in
eine Streckung oder Stauchung der Funktion in  -Richtung oder eine Spiegelung an der
-Richtung oder eine Spiegelung an der  -Achse bewirkt, sind die
-Achse bewirkt, sind die  -Koordinaten aller Extrempunkte unabhängig von
-Koordinaten aller Extrempunkte unabhängig von  Der Faktor
Der Faktor  von
von  ist stets ungleich Null und nach der Aufgabenstellung gilt
ist stets ungleich Null und nach der Aufgabenstellung gilt  Da
Da  gilt, wird
gilt, wird  somit genau dann Null, wenn
somit genau dann Null, wenn  Null wird. Nach Aufgabenteil a) besitzt
Null wird. Nach Aufgabenteil a) besitzt  eine lokale Extremstelle bei
eine lokale Extremstelle bei  damit muss auch
damit muss auch  dort eine lokale Extremstelle besitzen. Ein Extrempunkt der Funktion
dort eine lokale Extremstelle besitzen. Ein Extrempunkt der Funktion  liegt somit immer im Ursprung.
liegt somit immer im Ursprung.
f)
Da  sowie die Exponentialfunktion für alle
sowie die Exponentialfunktion für alle  größer oder gleich Null sind, muss eine Fallunterscheidung durchgeführt werden:
Fall 1:
größer oder gleich Null sind, muss eine Fallunterscheidung durchgeführt werden:
Fall 1: 

 Der Wertebereich von
Der Wertebereich von  für
für  ist somit gegeben durch
ist somit gegeben durch  Fall 2:
Fall 2: 

 Der Wertebereich von
Der Wertebereich von  für
für  ist somit gegeben durch
ist somit gegeben durch 
g)
Die Spiegelung an einer Geraden, die parallel zur  -Achse verläuft, entspricht einer Spiegelung an der
-Achse verläuft, entspricht einer Spiegelung an der  -Achse mit anschließender Verschiebung in
-Achse mit anschließender Verschiebung in  -Richtung. Da die Gerade, an der gespiegelt wird, durch die Gleichung
-Richtung. Da die Gerade, an der gespiegelt wird, durch die Gleichung  gegeben ist, wird zuerst an der
gegeben ist, wird zuerst an der  -Achse gespiegelt und anschließend um
-Achse gespiegelt und anschließend um  Längeneinheiten in
Längeneinheiten in  -Richtung verschoben. Somit folgt:
-Richtung verschoben. Somit folgt:
![\( \begin{array}[t]{rll}
s_{a}(x)&=& -h_a(x)+8 \\[5pt]
&=&- a\cdot x^2 \cdot \mathrm e^{- \frac{1}{20}x} +8
\end{array}\)](https://www.schullv.de/resources/formulas/77ff0f10062e1a05c8a7851b48a7ccd6dd1a73413df367128e5dc70da49f5765_light.svg)