Teil B

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ mit

$f_a(x)=\left(\dfrac{1}{2}-x\right)\cdot \text e^{a-x}$ $(a\,\epsilon\,\mathbb{R}).$

Gib die Koordinaten der Schnittpunkte der Graphen von $f_a$ mit den Koordinatenachsen an.

Ermittle den Wert für $a$ so, dass der Graph von $f_a$ die $y$ -Achse unter einem Winkel von $45^{\circ}$ schneidet.

(4 BE)

Berechne die Koordinaten der lokalen Extrempunkte und Wendepunkte der Graphen von $f_a.$

Gib zwei Eigenschaften für die Lage der Extrempunkte im Koordinatensystem an.

(8 BE)

Für jeden Wert von $a$ bilden die Punkte $S\left(\dfrac{1}{2} \mid f_a \left(\dfrac{1}{2}\right)\right)$ , $E \left(\dfrac{3}{2} \mid f_a \left(\dfrac{3}{2} \right)\right)$ und $W \left(\dfrac{5}{2} \mid f_a \left(\dfrac{5}{2} \right)\right)$ ein Dreieck.

Bestimme den Wert von $a,$ für den dieses Dreieck gleichschenklich mit der Basis $\overline{EW}$ ist.

(3 BE)

Der Anstieg einer Tangente im Punkt $W \left(\dfrac{5}{2} \mid f_a \left(\dfrac{5}{2} \right)\right)$ an einen Graphen von $f_a$ soll eine natürliche Zahl sein.

Ermittle eine zugehörige Tangentengleichung.

(3 BE)

Die Graphen der Schar $g_a$ ergeben sich, wenn die Graphen der Schar $f_a$ so in $x$ -Richtung verschoben werden, dass die Extrempunkte auf der $y$ -Achse liegen.

Gib die Verschiebung und eine Gleichung von $g_a$ an.

Begründe, dass kein Wert für $a$ existiert, so dass der Extrempunkt des Graphen der zugehörigen Funktion $g_a$ im Kooordinatenursprung liegt.

(3 BE)

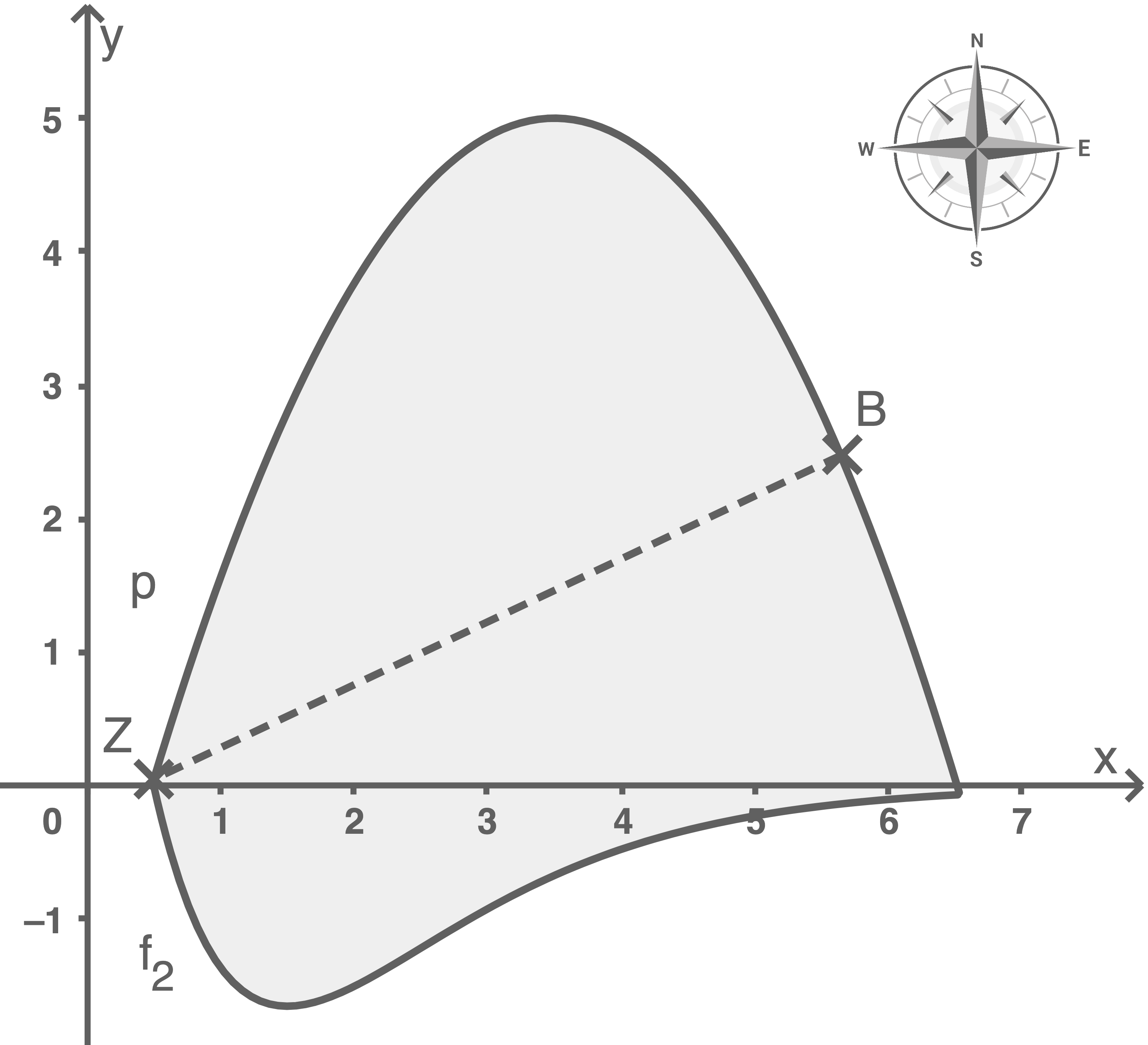
Das Ufer eines Sees kann im Süden durch den Graphen der Funktion $f_2$ mit
$f_2(x)=\left(\dfrac{1}{2}-x\right)\cdot \text e^{2-x}$
und im größeren, restlichen Bereich durch den Graphen einer quadratischen Funktion $p$ mathematisch modelliert werden. Der Zufluss zum See wird durch den Punkt $Z$ dargestellt. In der Darstellung liegt der Scheitelpunkt des Graphen von $p$ bei $S \left(\dfrac{7}{2} \mid 5\right)$ . Der Graph von $p$ schneidet den Graphen von $f_2$ im Punkt $Z \left(\dfrac{1}{2} \mid f_2 \left(\dfrac{1}{2} \right)\right)$ .

thüringen mathe abi 2021 teil b abbildung 1

Weise nach, dass $p(x)= -\dfrac{5}{9}x^2+\dfrac{35}{9}x-\dfrac{65}{36}$ eine Funktionsgleichung von $p$ ist.

(3 BE)

Eine Längeneinheit entspricht $20\,\text{m}$ in der Wirklichkeit.
Berechne die Größe der Fläche des Sees in Quadratmeter.

(4 BE)

Der südliche Teil des Sees wird als Badebereich freigegeben. Dieser soll aus Gründen des Naturschutzes nur die Hälfte der Gesamtfläche des Sees umfassen. Ausgehend vom Zufluss wird der Badebereich geradlinig mit Baumstämmen abgegrenzt.

Berechne die Koordinaten des Punktes $B,$ der den zweiten Befestigungspunkt der Baumstämme beschreibt.
Runde die Koordinaten von $B$ auf zwei Dezimalstellen genau.

(7 BE)

Im nördlichen Teil des Sees gibt es eine geschützte Wasserpflanzenart.
Die von den Pflanzen bedeckte Fläche kann mathematisch durch die Funktion $h$ mit $h(t)=\dfrac{80\cdot \text e^{0,11t}}{9+\text e^{0,11t}}$ beschreiben werden.
Dabei gibt $h(t)$ die von den Pflanzen bedeckte Fläche in Quadratmeter und $t$ die Beobachtungszeit in Tagen an.
Die Beobachtung beginnt zum Zeitpunkt $t=0$ und endet nach 80 Tagen.

Stelle den Graphen der Funktion $h$ im gegebenen Intervall dar.
Beschreibe die Größe der von den Pflanzen bedeckten Fläche anhand der graphischen Darstellung ab Beobachtungsbeginn.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Schnittpunkt mit der $y$ -Achse

$f_a(0) = \left( \dfrac{1}{2} - 0 \right) \cdot \mathrm{e}^{a-0} = \dfrac{1}{2} \cdot \mathrm{e}^{a}$

$S_y \left(0 \; \biggr\rvert \; \dfrac{1}{2} \cdot \mathrm{e}^{a} \right)$

Schnittpunkt mit der $x$ -Achse

$f_a(x)=0$

Mit Hilfe des solve-Befehls des CAS folgt $x=\frac{1}{2}.$ Somit ergibt sich folgender Schnittpunkt:

$S_x\left( \dfrac{1}{2} \; \biggr\rvert \; 0\right)$

Wert von $a$ ermitteln

Der Graph schneidet die $y$ -Achse in einem Winkel von $45^{\circ},$ wenn er auch die $x-$ Achse in diesem Winkel schneidet.
Damit der Graph die $x$ -Achse mit einem Winkel von $45^\circ$ schneidet muss Folgendes gelten:

$\( f_a$

Mit Hilfe des CAS wird die erste Ableitung von $f(x)$ bestimmt.

$\( f_a$

Wird die oben genannte Bedingung in den CAS eingegeben, so ergibt sich das folgende Ergebnis:

$a = \ln \left( \dfrac{2}{3} \right)$

Mit dem CAS folgt für die Ableitungen:

$\( f_a$

Notwendige Bedingung

$\( f_a$

Mit dem solve-Befehl des CAS folgt:

$x = \dfrac{3}{2}$

Hinreichende Bedingung

Da wegen der Positivität der $\mathrm e$ -Funktion $\( f_a$ gilt, ist die hinreichende Bedingung erfüllt und es handelt sich um einen Tiefpunkt.

$f_a \left( \dfrac{3}{2} \right) = - \mathrm{e}^{a - \frac{3}{2}}$

Somit hat der Tiefpunkt folgende Koordinaten:

$T_a \left(\dfrac{3}{2} \; \biggr\rvert \; - \mathrm{e}^{a - \frac{3}{2}} \right)$

Notwendige Bedingung

$\( f_a$

Mit dem solve-Befehl des CAS folgt:

$x = \dfrac{5}{2}$

Hinreichende Bedingung

Da wegen der Positivität der $\mathrm e$ -Funktion $\( f_a$ gilt, ist die hinreichende Bedingung erfüllt und es handelt sich um eine Linksrechtswendestelle.

$f_a \left( \dfrac{5}{2} \right) = - 2\mathrm{e}^{a - \frac{5}{2}}$

Somit hat der Wendepunkt folgende Koordinaten:

$W_a \left(\dfrac{5}{2} \; \biggr\rvert \; - 2\mathrm{e}^{a - \frac{5}{2}} \right)$

Zwei Eigenschaften:

Extrempunkte liegen im vierten Quadranten
Extrempunkte liegen auf der Gerade $x=\dfrac{3}{2}$

$f_a \left( \dfrac{1}{2} \right) = 0$

$f_a \left( \dfrac{3}{2} \right) = - \mathrm{e}^{a - \frac{3}{2}}$

$f_a \left( \dfrac{5}{2} \right) = - 2\mathrm{e}^{a - \frac{5}{2}}$

$|SE| = \sqrt{1^2 + \left( - \mathrm{e}^{a - \frac{3}{2}} \right)^2}$

$|SW| = \sqrt{2^2 + \left( - 2 \mathrm{e}^{a - \frac{5}{2}} \right)^2}$

Im gleichschenkligen Dreieck müssen die beiden Schenkel in der Länge übereinstimmen.

Aufstellen von $\mid SE\mid = \mid SW\mid$ im CAS liefert mit dem solve-Befehl:

$a \approx 2,44$

$\( f_a$

Ermitteln von $a$

Für $a = \dfrac{5}{2}$ ist $\( f_{\frac{5}{2}}$ und somit ist die Steigung an der Stelle $x = \dfrac{5}{2}$ eine natürliche Zahl.

Tangentengleichung ermitteln

$t(x)=1\cdot x+b$

Einsetzen des Punktes $W$ liefert mit dem solve-Befehl des CAS für $b:$

$b=-\dfrac{9}{2}$

Somit folgt $t(x)=x-\dfrac{9}{2}$

Die Extrempunkte der Schar $f_a$ liegen bei $x= \dfrac{3}{2} .$ Damit die Extrempunkte auf der $y$ -Achse liegen muss der Graph von $f_a$ um $\dfrac{3}{2}$ Längeneinheiten nach links verschoben werden. Es folgt:

$g_a (x)$ $= f_a \left(x + \dfrac{3}{2} \right)$ $= - \left(x + 1 \right) \cdot \mathrm{e}^{a-x-\frac{3}{2}}$

Damit der Extrempunkt im Ursprung liegt muss gelten: $g_a(0) = 0$

Aber es gilt $g_a(0) \lt 0$ für alle $a$ , da die $\mathrm e$ -Funktion stets ungleich null ist.

Somit ist die Gleichung nicht lösbar und der Extrempunkt kann nicht im Ursprung liegen.

$f_2\left(\dfrac{1}{2}\right) = \left(\dfrac{1}{2} - \dfrac{1}{2} \right) \cdot \mathrm{e}^{2-\frac{1}{2}} = 0$

$p\left(\dfrac{1}{2}\right)$ $= - \dfrac{5}{9} \cdot \left(\dfrac{1}{2}\right)^2 + \dfrac{35}{9} \cdot \dfrac{1}{2} - \dfrac{65}{36}$ $= 0$

Somit ist $f_2\left(\dfrac{1}{2}\right) = p\left(\dfrac{1}{2}\right)$

Der Scheitelpunkt einer Parabel ist immer auch ihr Extrempunkt. Für die Ableitung von $p(x)$ folgt:

$\(p$

Mit Hilfe des solve-Befehls des CAS folgt aus $\(p$

$x=\dfrac{7}{2}$

Da eine Parabel immer einen Extrempunkt besitzt, kann auf die Überprüfung der hinreichenden Bedingung verzichtet werden. Mit $p\left( \frac{7}{2} \right) = 5$ folgt, dass der angegebene Scheitelpunkt mit dem errechneten Scheitelpunkt übereinstimmt. Da damit beide der angegebenen Punkte übereinstimmen, ist $p(x)$ eine Funktionsgleichung von $p.$

Bestimmen der Schnittstellen von $p$ mit $f_2:$

Rechenweg anzeigen

$-\dfrac{5}{9}x^2+\dfrac{35}{9}x-\dfrac{65}{36}$ $= \left(\dfrac{1}{2}-x\right)\cdot \mathrm e^{2-x}$

Mit Hilfe des solve-Befehls des CAS folgt:

$x_1 = \dfrac{1}{2}$

$x_2 \approx 6,52$

$A_{\text{Modell}}$ $= \bigg \vert \displaystyle\int_{\frac{1}{2}}^{6,52}(p(x) -f_2(x))\;\mathrm dx\bigg \vert$ $= 24,405$

$A_{\text{Real}} = A_{\text{Modell}} \cdot (20\;\mathrm{m})^2$ $= 9761,832\;\mathrm{m}^2$

$A_1 = \dfrac{A_{\text{Modell}}}{2} \approx 12,2$

Funktionsgleichung der Baumstämme: $b(x) = m \cdot (x - 0,5)$

Es müssen folgende Gleichungen erfüllt werden:

$(1)$ $\displaystyle\int_{0,5}^{a}(p(x) -b(x))\;\mathrm dx = 12,2$

$(2)$ $p(a) = b(a)$

Die beiden Gleichungen bilden ein Gleichungssystem mit den beiden Variablen $a$ und $m.$ Lösung des Gleichungssystems im CAS ergibt:

$m \approx 0,51$

$a \approx 5,59$

Es folgt:

$p(5,59) \approx 2,58$

Somit ergeben sich die Koordinaten $B(5,59 \mid 2,58).$

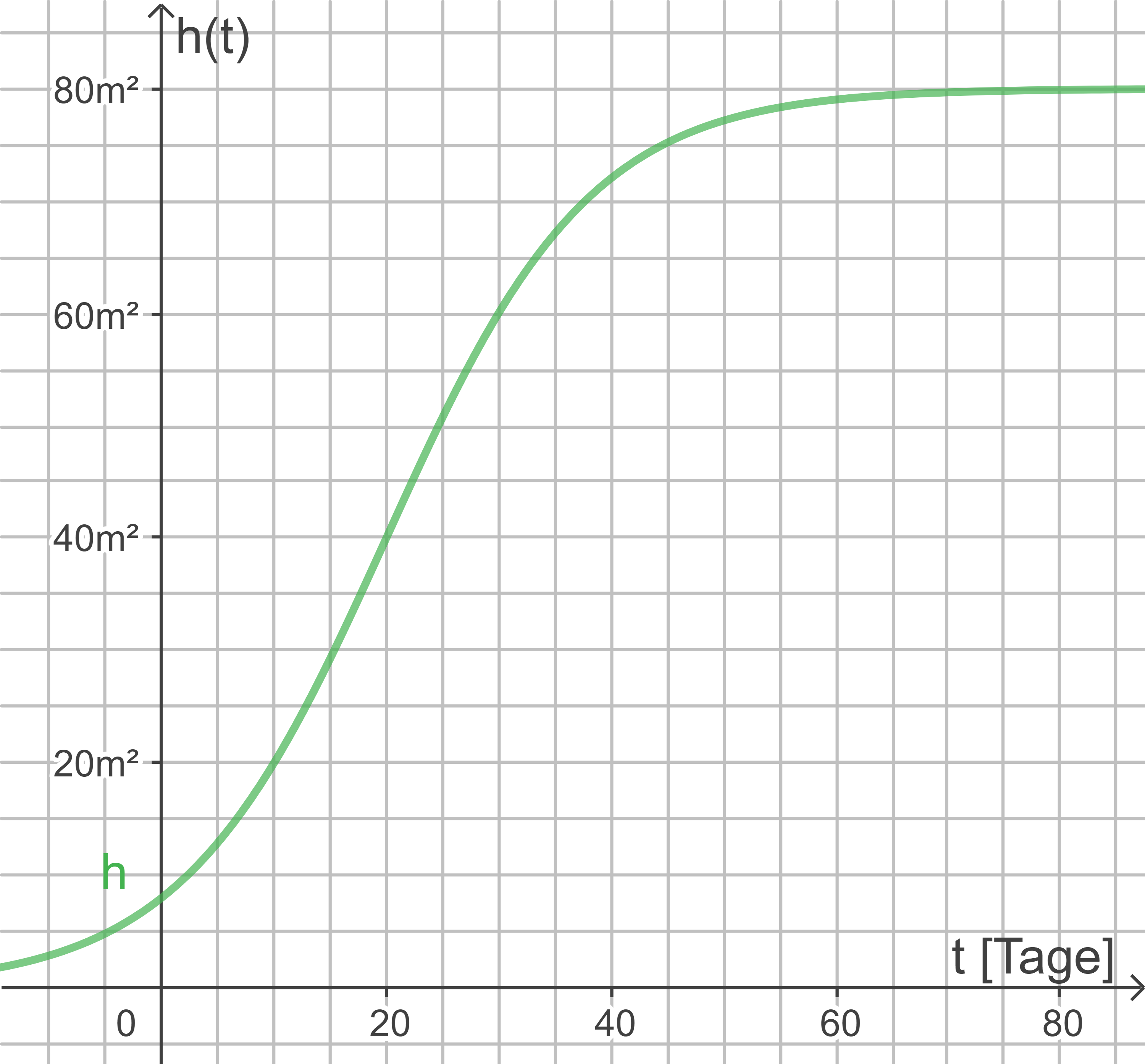
Grafik eines Wachstumsprozesses mit der Zeit in Tagen auf der x-Achse und Fläche in Quadratmetern auf der y-Achse.

Abb.: Funktion h(t)

Beschreibung:

Die von Pflanzen bedeckte Fläche wächst streng monoton.
Die Fläche wächst zu Beginn immer schneller, bis zum Wendepunkt bei ca. $t= 20\;\text{Tage}.$
Ab dem Wendepunkt nimmt das Wachstum der Fläche immer weiter ab.
Langfristig werden 80 Quadratmeter des Sees mit Planzen bedeckt sein.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?