Teil B1 - Analysis

Gegeben ist für jede positive reelle Zahl $k$ eine in $\mathbb{R}$ definierte Funktion $f_k.$

$f_k(x)=k \cdot x^3+2 \cdot k \cdot x^2-1$

Berechne die Koordinaten der lokalen Extrempunkte des Graphen von $f_k$ und weise deren Art nach.
Beschreibe den Einfluss von $k$ auf die Koordinaten dieser Punkte.

$\left[\text{Kontrollergebnis: } H_k\left(x_H\,\bigg\vert\, \dfrac{32}{27}k-1\right)\right]$

(6 BE)

Bestimme die Anzahl der Nullstellen von $f_k$ in Abhängigkeit von $k,$ ohne die Nullstellen zu berechnen.

(4 BE)

Berechne den kleinsten Anstieg aller Tangenten an den Graphen von $f_k$ in Abhängigkeit von $k.$

(3 BE)

Die Graphen der Funktionen $f_5$ und $f_{10}$ begrenzen eine Fläche $A$ vollständig. Berechne einen Wert für $k,$ für den die von den Graphen der Funktionen $f_5$ und $f_k$ vollständig eingeschlossene Fläche den doppelten Flächeninhalt der Fläche $A$ besitzt.

(5 BE)

Bei einer Operation wird für die Narkose ein Medikament verwendet, das im Laufe der Zeit vom Körper abgebaut wird. Die Restmenge des Medikaments in Milligramm, die nach $t$ Minuten im Körper einer Patientin noch vorhanden ist, kann bis zum Zeitpunkt des Aufwachens durch die Funktion $m$ mit

$m(t)=m_0 \cdot \mathrm{e}^{-0,0173 \cdot t}$

beschrieben werden. Dabei gibt $m_0$ die Menge des Medikaments in Milligramm zum Zeitpunkt $t = 0$ im Körper der Patientin an. Die Patientin wacht auf, wenn die Restmenge des Medikaments im Körper $0,5\;\text{mg}$ beträgt.

Berechne den Wert des Terms $\frac{m_0-m(30)}{m_0}$ und interpretiere dessen Bedeutung im Sachzusammenhang.

(3 BE)

Berechne die Mindestmenge des Medikaments, die sich zu Beginn einer einstündigen Narkose im Körper befinden müsste.

(2 BE)

Zu Beginn der Narkose befinden sich $2\;\text{mg}$ des Medikaments im Körper der Patientin.

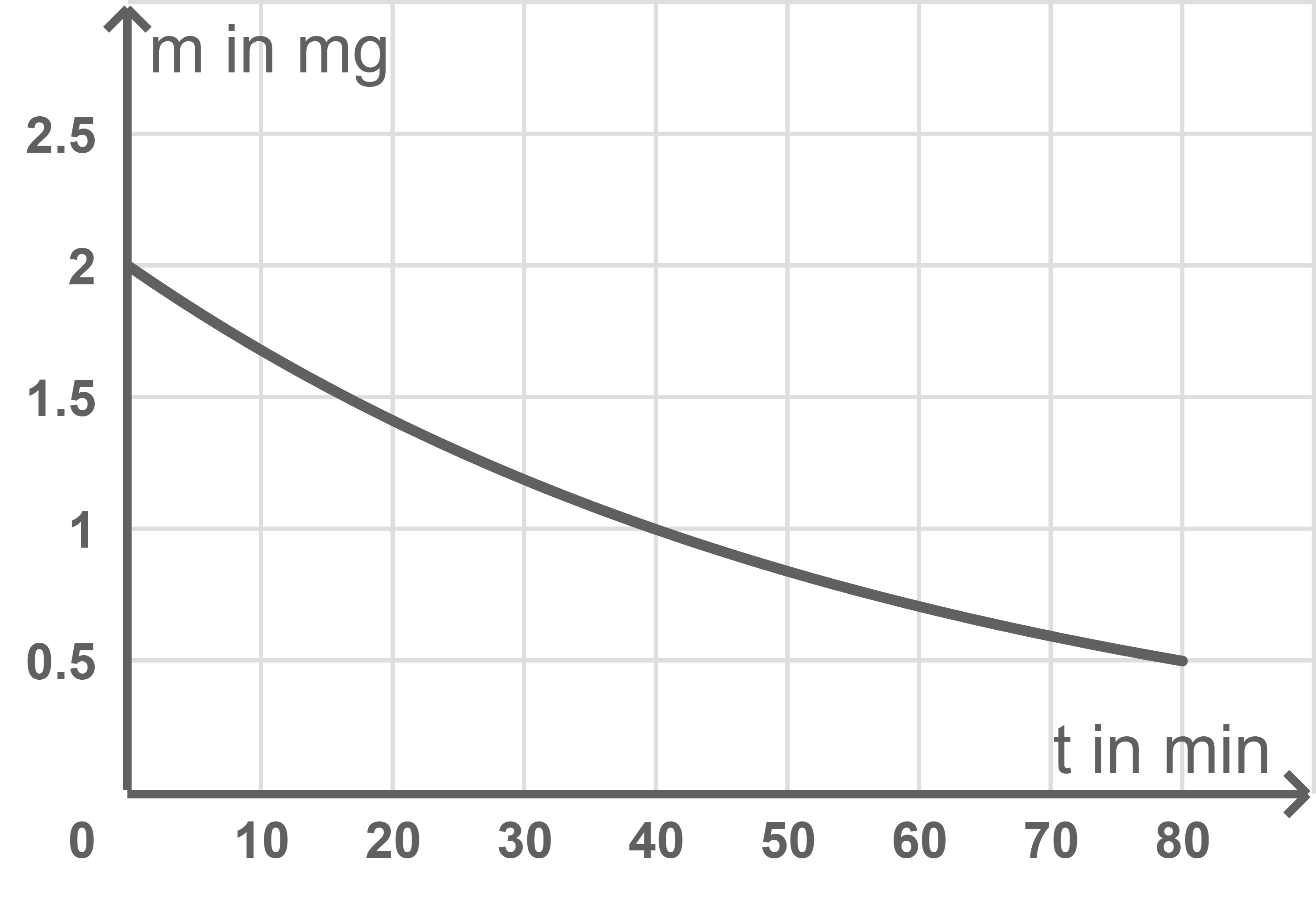
Stelle die Restmenge des Medikaments in Abhängigkeit von der Zeit für die Dauer der Narkose graphisch dar.

(2 BE)

Um die Dauer der Narkose zu verlängern, wird eine Stunde nach Beginn der Narkose nochmals $1\;\text{mg}$ des Medikaments direkt verabreicht. Ab dem Zeitpunkt des Aufwachens wird das Medikament linear mit der zum Zeitpunkt des Aufwachens vorliegenden Abbaurate des Medikaments abgebaut.
Ermittle die Zeitdauer vom Aufwachen bis zum Zeitpunkt, zu dem das Medikament im Körper vollständig abgebaut ist.

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Mit dem CAS folgt für die ersten beiden Ableitungen von $f_k:$

$\(\begin{array}[t]{rlll} f_k$

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(f_k$

Auflösen nach $x$ mit dem solve-Befehl des CAS liefert:

$\begin{array}[t]{rlll} x_1&=&-\dfrac{4}{3} \\[5pt] x_2&=&0 \end{array}$

2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen

$\(\begin{array}[t]{rlll} f_k$

Somit besitzt $f_k$ bei $x_1$ einen Hochpunkt und bei $x_2$ einen Tiefpunkt.

3. Schritt: Funktionswerte berechnen

Rechenweg anzeigen

$f_k\left(-\dfrac{4}{3}\right) = \dfrac{32}{27}k-1$

$\begin{array}[t]{rlll} f_k\left(0\right)&=&k\cdot0^3+2k\cdot0^2-1 \\[5pt] &=&-1 \end{array}$

Die Extrempunkte von $f_k$ sind damit durch $T(0\mid-1)$ und $H_k\left(-\frac{4}{3}\mid\frac{32}{27}k-1\right)$ gegeben. Der Wert von $k$ hat keinen Einfluss auf $T$ und auch keinen auf die $x$ -Koordinate von $H_k.$ Für verschiedene Werte von $k$ wird der Hochpunkt somit entlang der Geraden $x=-\frac{4}{3}$ verschoben.

Die Anzahl der Nullstellen von $f_k$ hängt nur von der Lage des Hochpunkts $H_k$ ab. Die $y$ -Koordinate des Punktes ist für $k=\frac{27}{32}$ gleich Null, für größere Werte von $k$ positiv und für kleinere negativ.
Damit besitzt $f_k$ eine Nullstelle, wenn $k\lt\frac{27}{32}$ gilt, zwei Nullstellen, wenn $k=\frac{27}{32}$ gilt und drei Nullstellen für $k\gt\frac{27}{32}.$

Für die dritte Ableitung von $f_k$ folgt:

$\(f_k$

Auflösen der notwendigen Bedingung $\(f_k$ nach $x$ mit dem CAS liefert:

$x=-\dfrac{2}{3}$

Da die dritte Ableitung immer größer als Null ist, ist das die Stelle mit minimaler Steigung. Einsetzen in $f_k$ liefert:

$\(\begin{array}[t]{rlll} f_k$

Auflösen der Gleichung $f_5(x)=f_k(x)$ nach $k$ liefert mit dem solve-Befehl des CAS:

$\begin{array}[t]{rlll} x_1&=&-2 \\[5pt] x_2&=&0 \end{array}$

Der Zusammenhang aus der Aufgabenstellung wird somit durch folgende Gleichung beschrieben:

$2\cdot\displaystyle\int_{-2}^{0}(f_{10}(x)-f_5(x))\;\mathrm dx$ $=\displaystyle\int_{-2}^{0}(f_k(x)-f_5(x))\;\mathrm dx$

Auflösen nach $k$ mit dem solve-Befehl des CAS liefert dann für den gesuchten Wert $k=15.$

Term berechnen

$\begin{array}[t]{rlll} \dfrac{m_0-m(30)}{m_0}&=&\dfrac{m_0-m_0\cdot\mathrm e^{-0,0173\cdot30}}{m_0} \\[5pt] &=&1-\mathrm e^{-0,519} \\[5pt] &\approx&0,405 \end{array}$

Bedeutung im Sachzusammenhang interpretieren

Der Term gibt den Anteil des Medikaments von der verabreichten Menge an, der in den ersten 30 Minuten abgebaut wird.

Auflösen der Gleichung $m(60)=0,5$ nach $m_0$ liefert mit dem solve-Befehl des CAS $m_0\approx1,41.$ Die Mindestmenge des Medikaments, die sich zu Beginn einer einstündigen Narkose im Körper befinden müsste, beträgt somit $1,41\;\text{mg}.$

Graph zeigt den Verlauf der Masse (in mg) über die Zeit (in Minuten).

Für die Menge des Medikaments nach einer Stunde gilt:

$\begin{array}[t]{rlll} m(60)&=&2\cdot\mathrm e^{-0,0173\cdot60}\\[5pt] &\approx&0,708\;\text{mg} \end{array}$

Da zu diesem Zeitpunkt nochmal $1\;\text{mg}$ verabreicht werden, ergibt sich zur Bestimmung des gesuchten Zeitpunkts $t$ folgende Gleichung:

$1,708 \cdot \mathrm{e}^{-0,0173 \cdot t}=0,5$

Mit dem solve-Befehl des CAS folgt:

$t\approx71,02$

Der CAS liefert für die erste Ableitung von $m:$

$\(m$

Für die Abbaurate des Medikaments zum obigen Zeitpunkt ergibt sich somit:

$\(\begin{array}[t]{rlll} m$

Einsetzen der Koordinaten $(71,02\mid0,5)$ in die allgemeine Gleichung $f(t)=-0,00865t+n$ liefert mit dem CAS für $n:$

$n\approx1,1143$

Nullsetzen der damit bestimmten Gleichung von $g$ liefert mit dem solve-Befehl des CAS für den gesuchten Zeitpunkt $t:$

$t\approx128,82$

Die Zeitdauer vom Aufwachen bis zu dem Zeitpunkt, an dem das Medikament vollständig abgebaut ist beträgt somit ca. $128,82-71,02=57,8$ Minuten.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?