Wahlaufgaben

Gegeben sind die in $\mathbb{R}_0^{+}$ definierten Funktionen $f$ und $g,$ wobei $g$ die Umkehrfunktion von $f$ ist. Die Abbildung zeigt die Graphen $G_f$ von $f$ und $G_g$ von $g.$ $G_f$ und $G_g$ schneiden sich nur im Koordinatenursprung und im Punkt $(x_S \mid f(x_S)).$ Beurteile die folgende Aussage:

$\displaystyle\int_{0}^{x_S}(g(x)-f(x))\;\mathrm dx= 2\cdot \displaystyle\int_{0}^{x_S}(x-f(x))\;\mathrm dx$

(5 BE)

Für jede positive reelle Zahl $a$ besitzt der Graph der Funktion $f_a$ mit $f_a(x)=\frac{1}{3} x^3+a \cdot x^2$ zwei lokale Extrempunkte.
Berechne den Wert für $a$ so, dass die Gerade durch die beiden Extrempunkte den Anstieg $-6$ besitzt.

(5 BE)

Gegeben ist die Schar der Ebenen $E_k: k \cdot x+(2-k) \cdot y=k$ mit $k \in \mathbb{R}.$

Es gibt eine Koordinatenebene, zu der alle Ebenen der Schar senkrecht stehen.
Gib diese an.

(1 BE)

Zeige, dass jeweils zwei verschiedene Ebenen der Schar nicht parallel zueinander sind.

(4 BE)

Der abgebildete Körper $ABCDEFGH$ ist Teil einer geraden Pyramide mit rechteckiger Grundfläche $EFGH.$ Die Rechtecke $ABCD$ und $EFGH$ liegen in zwei zueinander parallelen Ebenen mit dem Abstand $5.$ Der Flächeninhalt von EFGH ist viermal so groß wie der von $ABCD.$ Es gilt:

$A(0\mid0\mid 0), B(4\mid0\mid 0),$ $C(4\mid6\mid 0)$ und $D(0\mid6\mid 0)$

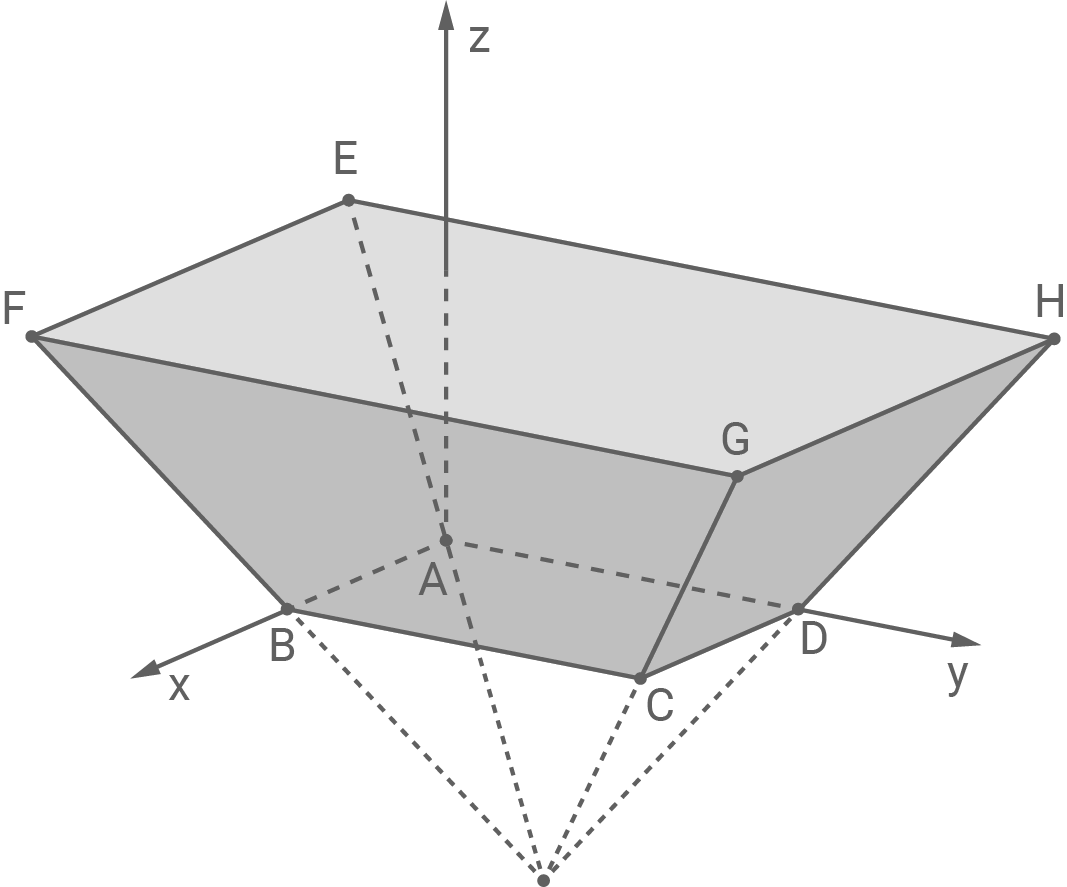
Gib eine Gleichung einer der beiden Symmetrieebenen des Körpers $ABCDEFGH$ an.

(1 BE)

Begründe, dass die Koordinaten des Punkts $F$ mit folgendem Term ermittelt werden können:

$\pmatrix{2\\3\\5}+2\cdot\left(\pmatrix{4\\0\\0}-\pmatrix{2\\3\\0}\right)$

(4 BE)

Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n$ und $p,$ mit $p \lt1.$
Es ist bekannt, dass $P(X=1)$ vierzehnmal so groß ist wie $P(X=0)$ und dass der Erwartungswert von $X$ gleich $10$ ist.
Berechne die Werte von $p$ und $n.$

(5 BE)

Betrachtet wird ein Würfel, dessen Seiten mit den Zahlen von $1$ bis $6$ durchnummeriert sind.

Der Würfel wird zweimal geworfen. Die Zufallsgröße $X$ gibt das Produkt der dabei erzielten Zahlen an.

Begründe, dass $P(X = 10) = P(X = 15)$ ist.

(2 BE)

Nun wird der Würfel $n$ -mal geworfen, wobei $n$ größer als $2$ ist. Ermittle einen Term, mit dem man die Wahrscheinlichkeit für das folgende Ereignis berechnen kann:

„Das Produkt der $n$ erzielten Zahlen ist $2,3$ oder $5.$ “

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die linke Seite der Gleichung gibt den Flächeninhalt der Fläche an, die $G_g$ und $G_f$ miteinander einschließen. Die rechte Seite der Gleichung gibt den doppelten Inhalt der Fläche an, die die Graphen der Gerade $y=x$ und $f$ miteinander einschließen.

Da $g$ die Umkehrfunktion von $f$ ist und somit durch Spiegelung von $f$ an der Gerade $y=x$ hervorgeht, hat die von $G_g$ und $G_f$ eingeschlossene Fläche den doppelten Inhalt wie die Fläche, die von der Graphen von $y=x$ und $f$ eingeschlossen wird. Damit ist die Aussage korrekt.

Für die Ableitung von $f$ folgt:

$\(f_a$

Anwenden der notwendigen Bedingung $\(f$ für Extremstellen liefert:

$\(\begin{array}[t]{rlll} f$

Mit dem Satz des Nullprodukts folgt $x_1=0$ und $x_2=-2a.$ Da der Graph von $f_a$ zwei Extrempunkte besitzt, kann auf die Überprüfung der hinreichenden Bedingung verzichtet werden. Einsetzen der Werte in $f_a$ liefert:

$\begin{array}[t]{rlll} f_a(0)&=&\dfrac{1}{3}\cdot0^3+a\cdot0^2\\[5pt] &=&0 \end{array}$

$\begin{array}[t]{rlll} f_a(-2a)&=&\dfrac{1}{3}\cdot(-2a)^3+a\cdot(-2a)^2\\[5pt] &=&-\dfrac{8}{3}\cdot a^3+4a^3\\[5pt] &=&\dfrac{4}{3}a^3 \end{array}$

Für die Steigung $m$ der Geraden durch die beiden Punkte folgt damit:

$\begin{array}[t]{rlll} m&=&6 \\[5pt] \dfrac{f_a(-2a)-f_a(0)}{-2a-0}&=&-6 \\[5pt] \dfrac{\frac{4}{3}a^3-0}{-2a-0}&=&-6 \\[5pt] -\frac{2}{3}a^2&=&-6 &\mid\;\cdot\left(-\frac{3}{2}\right)\\[5pt] a^2&=&9 &\mid\;\sqrt{\;} \\[5pt] a_{1;2}&=&\pm3 \end{array}$

Da der Wert von $a$ positiv sein muss, folgt somit $a=3.$

Alle Ebenengleichungen der Schar enthalten $z$ nicht. Somit stehen die Ebenen der Schar senkrecht zur $x$ - $y$ -Ebene.

Zwei Ebenen $E_{k_1}$ und $E_{k_2}$ der Schar sind genau dann parallel, wenn ihre Normalenvektoren Vielfache voneinander sind:

$\pmatrix{k_1\\2-k_1\\0}=a\cdot\pmatrix{k_2\\2-k_2\\0}$

Aus den ersten beiden Zeilen folgt:

$\begin{array}{lrll} \text{I}\quad&k_1&=& a\cdot k_2 \\ \text{II}\quad&2-k_1&=&a\cdot(2-k_2) \\ \end{array}$

Addieren von $\text{I}$ und $\text{II}$ liefert:

$\begin{array}[t]{rlll} 2&=&2a &\mid\;:2\\[5pt] 1&=&a \end{array}$

Der einzige mögliche Wert ist somit $a=1.$ Für diesen Wert sind die beiden Vektoren allerdings keine Vielfachen voneinander, sondern der gleiche Vektor und gehören somit zur gleichen Ebene. Zwei verschiedene Ebenen der Schar sind damit nicht parallel zueinander.

Eine mögliche Ebenengleichung ist gegeben durch $x=2.$

Da die Pyramide gerade ist, unterscheiden sich die Koordinaten der Mittelpunkte der beiden Rechtecke $ABCD$ und $EFGH$ nur in der $z$ -Koordinate. Anhand der Koordinaten der Eckpunkte des Rechtecks $ABCD$ folgt für den Mittelpunkt direkt:

$M(2\mid3\mid0)$

Mit der Anmerkung aus der Aufgabenstellung, dass die beiden Rechtecke um $5\;\text{LE}$ auseinander liegen, und der Darstellung der Pyramide in der Abbildung folgt für die Koordinaten des Mittelpunkts des Rechtecks $EFGH$ direkt $\(M$

Die Aufgabenstellung liefert zudem, dass der Flächeninhalt von $EFGH$ viermal so groß ist, wie der von $ABCD.$ Da die Pyramide gerade ist, sind die beiden Rechtecke ähnlich und es gilt somit, dass die Diagonalen von $EFGH$ doppelt so lang sind wie die von $ABCD.$ Insgesamt folgt damit für den Ortsvektor des Punktes $F:$

$\(\begin{array}[t]{rlll} \overrightarrow{OF}&=&\overrightarrow{OM$

Für $p$ gilt, da $n\cdot p$ der Erwartungswert von $X$ ist:

Rechenweg anzeigen

$p=\dfrac{2}{7}$

Damit ergibt sich für $n:$

$\begin{array}[t]{rlll} n\cdot p&=&10 \\[5pt] n\cdot \dfrac{2}{7}&=&10 &\mid\;\cdot\frac{7}{2} \\[5pt] n&=&35 \end{array}$

Sowohl $10$ als auch $15$ können jeweils nur durch genau ein Produkt von zwei Zahlen erhalten werden, nämlich das Produkt von $2$ und $5$ bzw. das Produkt von $3$ und $5.$ Hierbei ist egal, in welcher Reihenfolge die beiden Zahlen gewürfelt werden, d.h. es gibt jeweils zwei Ergebnisse, die $X=10$ bzw. $X=15$ liefern. Da jede zahl auf dem Würfel mit gleicher Wahrscheinlichkeit erzielt wird, gilt damit $P(X=10)=P(X=15).$

Die Zahlen $2,3$ und $5$ sind Primzahlen. Somit ist die einzige Möglichkeit, dass das Produkt der $n$ erzielten Zahlen $2,3$ oder $5$ ist, dass $(n-1)$ -mal die Zahl $1$ gewürfelt wird, und einmal $2,3$ bzw. $5.$ Da es $n$ mögliche Würfe gibt, in denen die Zahl ungleich $1$ gewürfelt werden kann, folgt für die gesuchte Wahrscheinlichkeit $p$ somit:

$p=3\cdot n\cdot\dfrac{1}{6}\cdot\left(\dfrac{1}{6}\right)^{n-1}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?