Teil B2
Gegeben ist die Funktion  durch
durch 

a)
Durch Spiegelung des Graphen von  an der
an der  -Achse entsteht der Graph von
-Achse entsteht der Graph von  . Der Graph von
. Der Graph von  entsteht durch Spiegelung des Graphen von
entsteht durch Spiegelung des Graphen von  an der Geraden
an der Geraden  . Der Graph von
. Der Graph von  entsteht durch Verschiebung des Graphen von
entsteht durch Verschiebung des Graphen von  derart, dass der Tiefpunkt des Graphen von
derart, dass der Tiefpunkt des Graphen von  im Koordinatenursprung liegt.
im Koordinatenursprung liegt.
Gib je eine Funktionsgleichung von ,
,  und
und  an.
an.
Gib je eine Funktionsgleichung von
(3 BE)
b)
In den Extrempunkten und in den beiden vom Koordinatenursprung verschiedenen Schnittpunkten des Graphen von  mit der
mit der  -Achse werden die Tangenten an den Graphen von
-Achse werden die Tangenten an den Graphen von  gelegt. Diese Tangenten bilden ein Viereck.
gelegt. Diese Tangenten bilden ein Viereck.
Begründe, dass dieses Viereck ein Parallelogramm ist.
Berechne dessen Flächeninhalt und die Größe eines Innenwinkels.
Begründe, dass dieses Viereck ein Parallelogramm ist.
Berechne dessen Flächeninhalt und die Größe eines Innenwinkels.
(4 BE)
c)
Für jede positive reelle Zahl  ist durch
ist durch  eine Gerade
eine Gerade  gegeben. Der Graph von
gegeben. Der Graph von  begrenzt mit der
begrenzt mit der  -Achse im I. Quadranten die Fläche
-Achse im I. Quadranten die Fläche  vollständig. Der Graph von
vollständig. Der Graph von  teilt die Fläche
teilt die Fläche  in zwei Teilflächen.
in zwei Teilflächen.
Zeige, dass das Verhältnis der Teilflächen beträgt.
beträgt.
Ermittle den Wert für so, dass die Gerade
so, dass die Gerade  die Fläche
die Fläche  in zwei gleich große Flächen teilt.
in zwei gleich große Flächen teilt.
Zeige, dass das Verhältnis der Teilflächen
Ermittle den Wert für
(5 BE)
d)
In einem Betrieb fallen Abfallstücke, welche die Form der Fläche  aus Teilaufgabe c) haben, an.
aus Teilaufgabe c) haben, an.
Untersuche, ob man aus einem solchen Stück (siehe Abbildung) ein Quadrat mit der Seitenlänge ausschneiden kann.
ausschneiden kann.
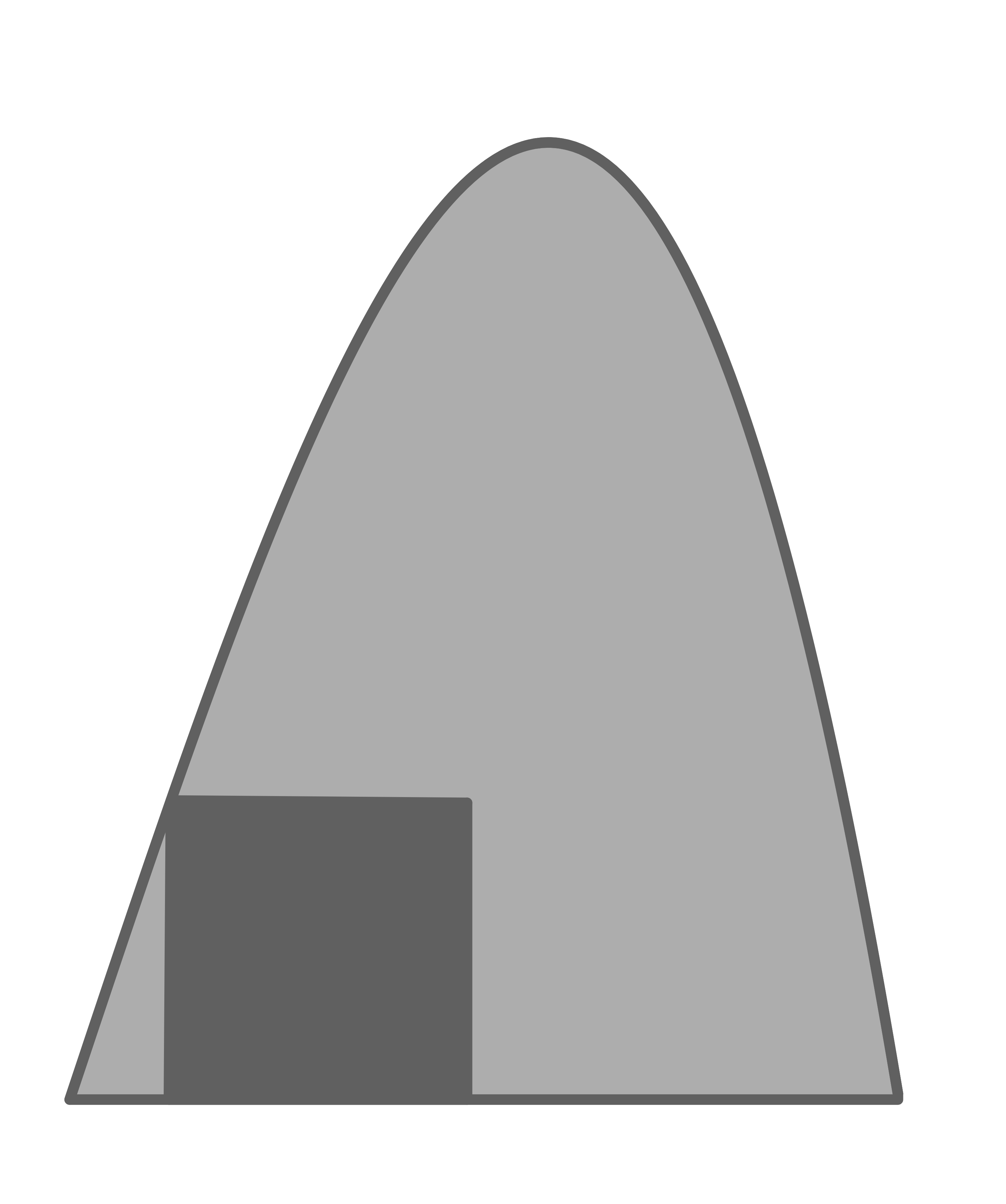
Untersuche, ob man aus einem solchen Stück (siehe Abbildung) ein Quadrat mit der Seitenlänge

(3 BE)
e)
Für jede positive reelle Zahl  ist eine Funktion
ist eine Funktion  gegeben durch
gegeben durch 
 . Beschreibe, wie die Graphen von
. Beschreibe, wie die Graphen von  aus dem Graphen von
aus dem Graphen von  in Abhängigkeit von
in Abhängigkeit von  hervorgehen.
hervorgehen.
Der Hochpunkt und die Schnittpunkte des Graphen von mit der
mit der  -Achse
-Achse  bilden ein Dreieck.
bilden ein Dreieck.
Berechne alle Werte für so, dass das Dreieck gleichschenklig ist.
so, dass das Dreieck gleichschenklig ist.
Der Hochpunkt und die Schnittpunkte des Graphen von
Berechne alle Werte für
(5 BE)
a)
Funktionsgleichung von  angeben
angeben
 Funktionsgleichung von
Funktionsgleichung von  angeben
Die Gerade
angeben
Die Gerade  verläuft parallel zur
verläuft parallel zur  -Achse und im Abstand von
-Achse und im Abstand von  überhalb von dieser. Eine Spiegelung an der Geraden
überhalb von dieser. Eine Spiegelung an der Geraden  entspricht somit einer Spiegelung an der
entspricht somit einer Spiegelung an der  -Achse mit anschließender Verschiebung um
-Achse mit anschließender Verschiebung um  in
in  -Richtung:
-Richtung:
 Funktionsgleichung von
Funktionsgleichung von  angeben
Mit der graphischen Darstellung im CAS folgt, dass der Tiefpunkt von
angeben
Mit der graphischen Darstellung im CAS folgt, dass der Tiefpunkt von  die Koordinaten
die Koordinaten  besitzt. Der Graph von
besitzt. Der Graph von  entsteht somit aus dem Graphen von
entsteht somit aus dem Graphen von  durch eine Verschiebung um
durch eine Verschiebung um  in
in  -Richtung und um
-Richtung und um  in
in  -Richtung:
-Richtung:

b)
Parallelogramm begründen
Da  gilt, ist der Graph der Funktion
gilt, ist der Graph der Funktion  punktsymmetrisch zum Ursprung. Damit besitzen die beiden Tangenten an die Nullstellen von
punktsymmetrisch zum Ursprung. Damit besitzen die beiden Tangenten an die Nullstellen von  die gleiche Steigung, sind also parallel zueinander. Da zudem in den beiden Extrempunkten
die gleiche Steigung, sind also parallel zueinander. Da zudem in den beiden Extrempunkten  gelten muss, liegen auch diese beiden Tangenten parallel zueinander. Somit handelt es sich bei dem Viereck um ein Parallelogramm.
Flächeninhalt des Parallelogramms berechnen
Für den Flächeninhalt eines Parallelogramms gilt
gelten muss, liegen auch diese beiden Tangenten parallel zueinander. Somit handelt es sich bei dem Viereck um ein Parallelogramm.
Flächeninhalt des Parallelogramms berechnen
Für den Flächeninhalt eines Parallelogramms gilt  wobei
wobei  bzw.
bzw.  die in dieser Hilfsabbildung eingezeichneten Längen bezeichnen:
die in dieser Hilfsabbildung eingezeichneten Längen bezeichnen:
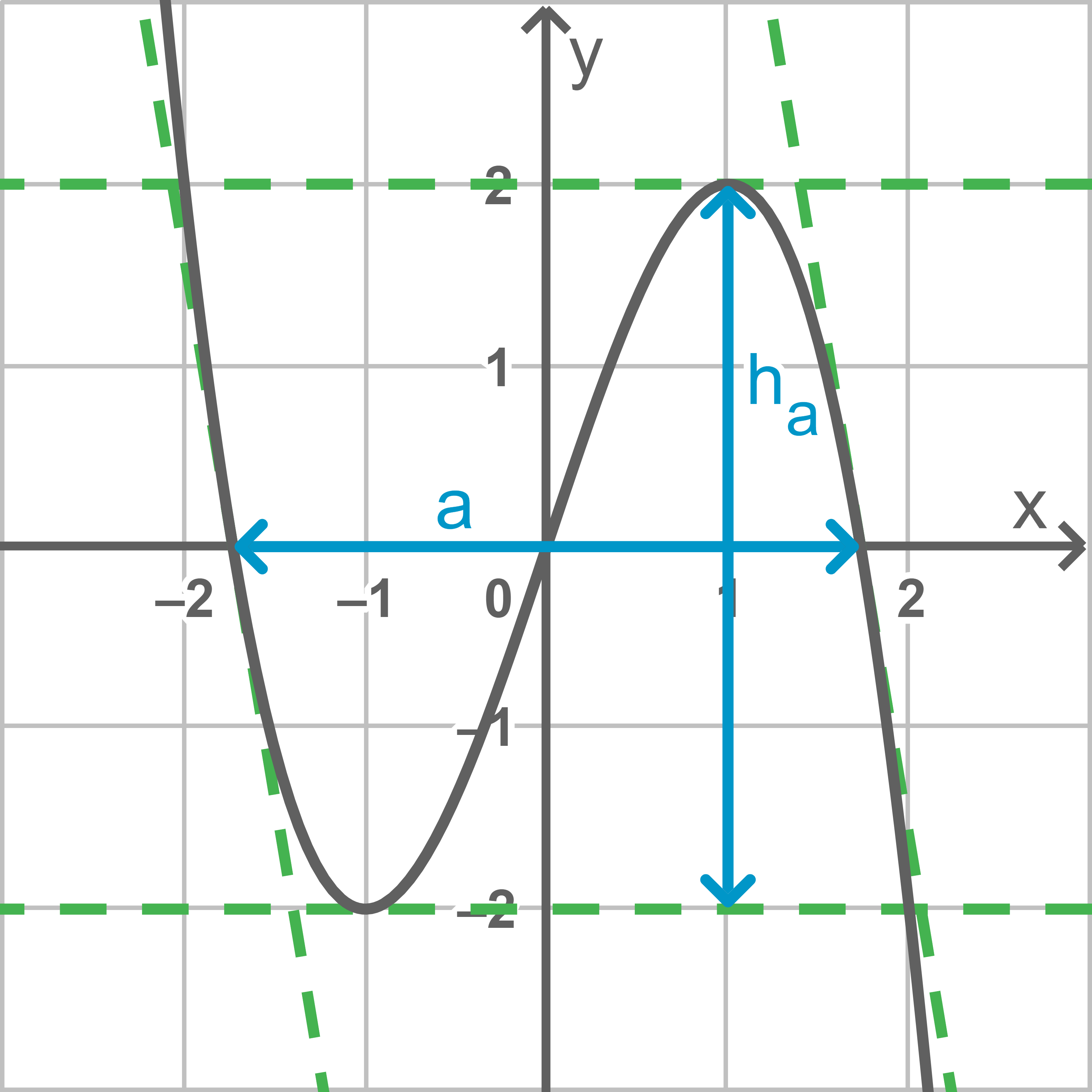 Mit Hilfe des solve-Befehls des CAS liefert
Mit Hilfe des solve-Befehls des CAS liefert 
![\(\begin{array}[t]{rll}
x_1&=&-\sqrt{3} \\[5pt]
x_2&=&0 \\[5pt]
x_3&=&\sqrt{3}
\end{array}\)](https://www.schullv.de/resources/formulas/bc62bcf8eed64b17495f4b47aebee32ace47ee6d3199a60b5c770865ad56107a_light.svg) Somit gilt
Somit gilt  Aus Aufgabenteil a) folgt, dass der Tiefpunkt
Aus Aufgabenteil a) folgt, dass der Tiefpunkt  von
von  die
die  -Koordinate
-Koordinate  besitzt, das heißt da
besitzt, das heißt da  punktsymmetrisch zum Ursprung ist, besitzt der Hochpunkt
punktsymmetrisch zum Ursprung ist, besitzt der Hochpunkt  von
von  die
die  _Koordinate
_Koordinate  Somit folgt
Somit folgt  Insgesamt besitzt das Parallelogramm damit einen Flächeninhalt von
Insgesamt besitzt das Parallelogramm damit einen Flächeninhalt von  Innenwinkel des Parallelogramms bestimmen
Innenwinkel des Parallelogramms bestimmen
 Für die Steigung dieser Tangente gilt somit
Für die Steigung dieser Tangente gilt somit  Da die obere und untere Seite des Parallelogramms parallel zur
Da die obere und untere Seite des Parallelogramms parallel zur  -Achse verlaufen, folgt somit für den rechten oberen Innenwinkel mit dem CAS:
-Achse verlaufen, folgt somit für den rechten oberen Innenwinkel mit dem CAS:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&m \\[5pt]
\tan(\alpha)&=&-6 \\[5pt]
\alpha&\approx&99,46^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/6c4038b2fe34b2a33d0e3ac8380c1393f081508f0a48119a1eb47bf2379ff871_light.svg) Die Größe des einen Innenwinkels beträgt somit ca.
Die Größe des einen Innenwinkels beträgt somit ca. 

Mit Hilfe des CAS folgt für die Funktionsgleichung der Tangente an  in beispielsweise
in beispielsweise 


c)
Verhältnis von  zeigen
Mit Hilfe der Nullstellen von
zeigen
Mit Hilfe der Nullstellen von  aus Aufgabenteil b) folgt durch Integrieren mit Hilfe des CAS für den Flächeninhalt der Fläche
aus Aufgabenteil b) folgt durch Integrieren mit Hilfe des CAS für den Flächeninhalt der Fläche 
 Für die Schnittstellen des Graphen von
Für die Schnittstellen des Graphen von  mit dem Graphen von
mit dem Graphen von  an denen
an denen  gilt, folgt mit dem solve-Befehl des CAS:
gilt, folgt mit dem solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
x_1&=&-\sqrt{2} \\[5pt]
x_2&=&0 \\[5pt]
x_3&=&\sqrt{2}
\end{array}\)](https://www.schullv.de/resources/formulas/f31708d104f3eccacc517259817cfb759ef8a773124a7fb9b4f080ec49bc8c36_light.svg) Von diesen Schnittstellen liegt nur
Von diesen Schnittstellen liegt nur  im I. Quadranten und ist somit die gesuchte Schnittstelle der beiden Graphen.
Der Flächeninhalt der Teilfläche zwischen
im I. Quadranten und ist somit die gesuchte Schnittstelle der beiden Graphen.
Der Flächeninhalt der Teilfläche zwischen  und
und  ergibt sich somit mit Hilfe des CAS wie folgt:
ergibt sich somit mit Hilfe des CAS wie folgt:
![\(\begin{array}[t]{rll}
A_1&=&\displaystyle\int_{0}^{\sqrt{2}}(f(x)-g_1(x))\;\mathrm dx \\[5pt]
&=&1\;[\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/a6d6fd85885fb3f6b15390ac306eb18a9399cf88ccaee0fa8c7e433dd2226152_light.svg) Für den Flächeninhalt der unteren Teilfläche folgt somit:
Für den Flächeninhalt der unteren Teilfläche folgt somit:
![\(A_2=A_A-A_1=1,25\;[\text{FE}]\)](https://www.schullv.de/resources/formulas/35934ef6b98a4c7631de821a031d30cf2e7c839cc5bd2737567ad954ad76fdcb_light.svg) Für das Verhältnis der Teilflächen gilt damit:
Für das Verhältnis der Teilflächen gilt damit:
 Wert für
Wert für  bestimmen
Mit Hilfe des Flächeninhalts der Fläche
bestimmen
Mit Hilfe des Flächeninhalts der Fläche  folgt, dass beide Teilfächen
folgt, dass beide Teilfächen ![\(\frac{1}{2}\cdot2,25=1,125\;[\text{FE}]\)](https://www.schullv.de/resources/formulas/ee6f2fb0cb78fa216f6155d1398510ba6e401d405e84be4fdb69be91e24e0d90_light.svg) groß sein müssen. Für die Schnittpunkte von
groß sein müssen. Für die Schnittpunkte von  und
und  folgt mit Hilfe des solve-Befehls des CAS:
folgt mit Hilfe des solve-Befehls des CAS:
 Für diese Schnittstellen kann sich der jeweilige Schnittpunkt nur für
Für diese Schnittstellen kann sich der jeweilige Schnittpunkt nur für  im I. Quadranten befinden. Damit die beiden Teilflächen gleichgroß sind, muss also folgende Gleichung gelten:
im I. Quadranten befinden. Damit die beiden Teilflächen gleichgroß sind, muss also folgende Gleichung gelten:
 Mit dem solve-Befehl des CAS folgt damit für
Mit dem solve-Befehl des CAS folgt damit für 
![\(\begin{array}[t]{rll}
m_1&\approx&0,88 \\[5pt]
m_2&\approx&-5,12
\end{array}\)](https://www.schullv.de/resources/formulas/00c49098f3bf6d25008863a161c23d3e8f64101138fa443e81f92fe0da6fe613_light.svg)
 Sowohl
Sowohl  als auch
als auch  erfüllen die Bedingung
erfüllen die Bedingung  allerdings verläuft
allerdings verläuft  für
für  bei positiven
bei positiven  -Werten komplett unterhalb der
-Werten komplett unterhalb der  -Achse, sodass der Schnittpunkt mit
-Achse, sodass der Schnittpunkt mit  nicht im I. Quadranten liegen kann. Die Gerade
nicht im I. Quadranten liegen kann. Die Gerade  teilt die Fläche
teilt die Fläche  somit für den Wert
somit für den Wert  in zwei gleich große Flächen.
in zwei gleich große Flächen.
falls
falls


d)
Mit Hilfe des solve-Befehls des CAS folgt für die Lösungen der Gleichung 
![\(\begin{array}[t]{rll}
x_1&\approx&-1,89 \\[5pt]
x_2&\approx&0,39 \\[5pt]
x_3&\approx&1,51
\end{array}\)](https://www.schullv.de/resources/formulas/4cfdb02ba96bca4cd7777808cdae56e90d88b09a0020bd329a000af24989a2fc_light.svg) Von diesen Lösungen liegen nur die zu
Von diesen Lösungen liegen nur die zu  und
und  gehörenden Funktionswerte im betrachteten I. Quadranten.
gehörenden Funktionswerte im betrachteten I. Quadranten.
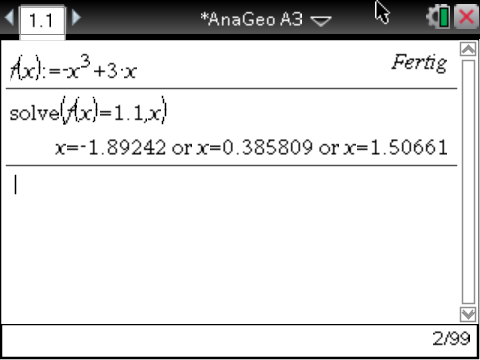 Damit ein Quadrat mit der Seitenlänge
Damit ein Quadrat mit der Seitenlänge  in die Fläche passt, muss der Abstand zwischen
in die Fläche passt, muss der Abstand zwischen  und
und  größer oder gleich
größer oder gleich  sein. Für die Differenz gilt:
sein. Für die Differenz gilt:
![\(x_3-x_2 \approx 1,12\gt1,1\;[\text{LE}]\)](https://www.schullv.de/resources/formulas/3c0d5d2617419f4973d7e78d5151646a3626cd6f24f6ebbed169de8f1ab981e3_light.svg) Es folgt, dass man ein Quadrat mit der Seitenlänge
Es folgt, dass man ein Quadrat mit der Seitenlänge  aus der betrachteten Fläche ausschneiden kann.
aus der betrachteten Fläche ausschneiden kann.

e)
Graphen von  beschreiben
Es gilt
beschreiben
Es gilt 
 das heißt die Graphen von
das heißt die Graphen von  gehen aus dem Graphen von
gehen aus dem Graphen von  durch eine Streckung bzw. Stauchung entlang der
durch eine Streckung bzw. Stauchung entlang der  -Achse hervor.
Werte von
-Achse hervor.
Werte von  für gleichschenkliges Dreieck berechnen
Da die Graphen von
für gleichschenkliges Dreieck berechnen
Da die Graphen von  durch Streckung bzw. Stauchung entlang der
durch Streckung bzw. Stauchung entlang der  -Achse aus dem Graphen von
-Achse aus dem Graphen von  hervorgehen, besitzen alle Funktionen dieselben Nullstellen wie
hervorgehen, besitzen alle Funktionen dieselben Nullstellen wie  das heißt nach Aufgabenteil b) lauten die beiden gesuchten Nullstellen
das heißt nach Aufgabenteil b) lauten die beiden gesuchten Nullstellen  und
und 
Zudem ergeben sich die jeweiligen Hochpunkte durch Streckung bzw. Stauchung mit entlang der
entlang der  -Achse aus dem von
-Achse aus dem von  das heißt sie besitzen nach Aufgabenteil b) die Koordinaten
das heißt sie besitzen nach Aufgabenteil b) die Koordinaten  Damit das Dreick aus den Punkten mit den Koordinaten
Damit das Dreick aus den Punkten mit den Koordinaten  und
und  gleichschenklig ist, müssen mindestens zwei Seiten gleichlang sein.
gleichschenklig ist, müssen mindestens zwei Seiten gleichlang sein.
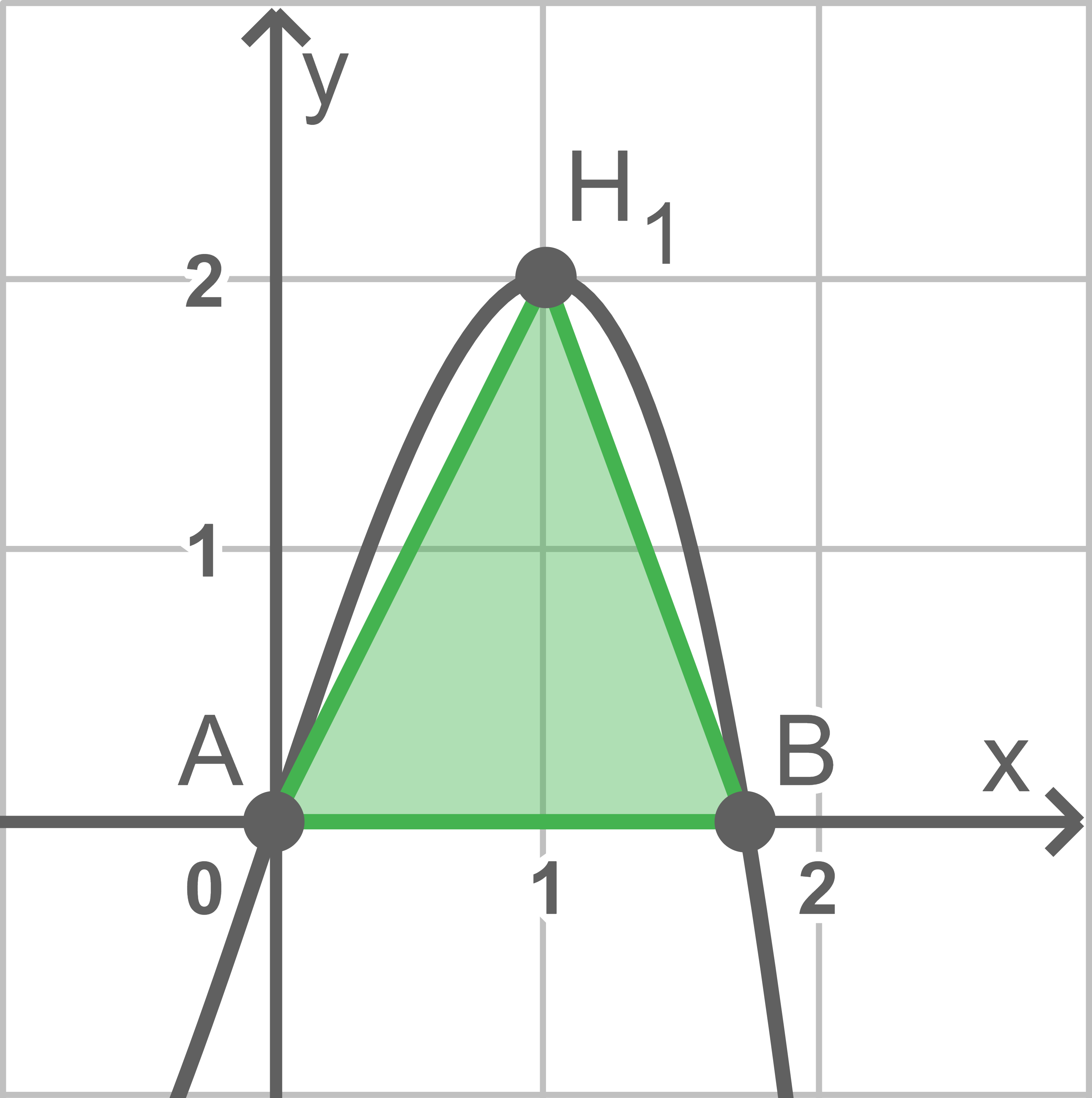 Da die Strecke
Da die Strecke  auf der
auf der  -Achse verläuft und der
-Achse verläuft und der  -Wert von
-Wert von  für alle
für alle  nicht in der Mitte dieser Strecke liegt, wie in der Skizze für
nicht in der Mitte dieser Strecke liegt, wie in der Skizze für  verdeutlicht, kann
verdeutlicht, kann  für kein
für kein  gelten.
Die Länge der Seite
gelten.
Die Länge der Seite  ergibt sich als
ergibt sich als ![\(\left\vert\overrightarrow{AB}\right\vert = 3\;[\text{LE}].\)](https://www.schullv.de/resources/formulas/d0c8073af4a295f67d766f8b428094e2187ba6469660f181bd12a4da1e5c472a_light.svg) Für
Für ![\(\left\vert\overrightarrow{AH_k}\right\vert = 3\;[\text{LE}]\)](https://www.schullv.de/resources/formulas/204d1c578f9dc03fa4bba0e194417ff5407e0de6a3b820f7b3c2c28c5a65fe9c_light.svg) liefert der solve-Befehl des CAS:
liefert der solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
k_1&=&-\dfrac{\sqrt{2}}{2} \\[5pt]
k_2&=&\dfrac{\sqrt{2}}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/6c4c6d8b8ef7049958905d8a42a817fc3051850a83c049f8e9fe7270d4dda322_light.svg) Für die andere Möglichkeit,
Für die andere Möglichkeit, ![\(\left\vert\overrightarrow{BH_k}\right\vert = 3\;[\text{LE}],\)](https://www.schullv.de/resources/formulas/adb4000953a66e3eac0dfbabea7327070ec1d4e7887fa891c97e852b3c8d989f_light.svg) ergibt sich mit Hilfe des solve-Befehls des CAS:
ergibt sich mit Hilfe des solve-Befehls des CAS:
![\(\begin{array}[t]{rll}
k_3&=&-\dfrac{\sqrt{2\cdot\sqrt{3}-1}}{2} \\[5pt]
k_4&=&\dfrac{\sqrt{2\cdot\sqrt{3}-1}}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/3ed5a97c472255f6a539b3adea2833ef1504d39270e8923654ea857fbcb0c94e_light.svg) Da
Da  laut Aufgabenstellung eine positive reelle Zahl ist, ist das betrachtete Dreieck nur für die Werte
laut Aufgabenstellung eine positive reelle Zahl ist, ist das betrachtete Dreieck nur für die Werte  und
und  gleichschenklig.
gleichschenklig.
Zudem ergeben sich die jeweiligen Hochpunkte durch Streckung bzw. Stauchung mit

a)
Funktionsgleichung von  angeben
angeben
 Funktionsgleichung von
Funktionsgleichung von  angeben
Die Gerade
angeben
Die Gerade  verläuft parallel zur
verläuft parallel zur  -Achse und im Abstand von
-Achse und im Abstand von  überhalb von dieser. Eine Spiegelung an der Geraden
überhalb von dieser. Eine Spiegelung an der Geraden  entspricht somit einer Spiegelung an der
entspricht somit einer Spiegelung an der  -Achse mit anschließender Verschiebung um
-Achse mit anschließender Verschiebung um  in
in  -Richtung:
-Richtung:
 Funktionsgleichung von
Funktionsgleichung von  angeben
Mit der graphischen Darstellung im CAS folgt, dass der Tiefpunkt von
angeben
Mit der graphischen Darstellung im CAS folgt, dass der Tiefpunkt von  die Koordinaten
die Koordinaten  besitzt. Der Graph von
besitzt. Der Graph von  entsteht somit aus dem Graphen von
entsteht somit aus dem Graphen von  durch eine Verschiebung um
durch eine Verschiebung um  in
in  -Richtung und um
-Richtung und um  in
in  -Richtung:
-Richtung:

b)
Parallelogramm begründen
Da  gilt, ist der Graph der Funktion
gilt, ist der Graph der Funktion  punktsymmetrisch zum Ursprung. Damit besitzen die beiden Tangenten an die Nullstellen von
punktsymmetrisch zum Ursprung. Damit besitzen die beiden Tangenten an die Nullstellen von  die gleiche Steigung, sind also parallel zueinander. Da zudem in den beiden Extrempunkten
die gleiche Steigung, sind also parallel zueinander. Da zudem in den beiden Extrempunkten  gelten muss, liegen auch diese beiden Tangenten parallel zueinander. Somit handelt es sich bei dem Viereck um ein Parallelogramm.
Flächeninhalt des Parallelogramms berechnen
Für den Flächeninhalt eines Parallelogramms gilt
gelten muss, liegen auch diese beiden Tangenten parallel zueinander. Somit handelt es sich bei dem Viereck um ein Parallelogramm.
Flächeninhalt des Parallelogramms berechnen
Für den Flächeninhalt eines Parallelogramms gilt  wobei
wobei  bzw.
bzw.  die in dieser Hilfsabbildung eingezeichneten Längen bezeichnen:
die in dieser Hilfsabbildung eingezeichneten Längen bezeichnen:
 Mit Hilfe des solve-Befehls des CAS liefert
Mit Hilfe des solve-Befehls des CAS liefert 
![\(\begin{array}[t]{rll}
x_1&=&-\sqrt{3} \\[5pt]
x_2&=&0 \\[5pt]
x_3&=&\sqrt{3}
\end{array}\)](https://www.schullv.de/resources/formulas/bc62bcf8eed64b17495f4b47aebee32ace47ee6d3199a60b5c770865ad56107a_light.svg) Somit gilt
Somit gilt  Aus Aufgabenteil a) folgt, dass der Tiefpunkt
Aus Aufgabenteil a) folgt, dass der Tiefpunkt  von
von  die
die  -Koordinate
-Koordinate  besitzt, das heißt da
besitzt, das heißt da  punktsymmetrisch zum Ursprung ist, besitzt der Hochpunkt
punktsymmetrisch zum Ursprung ist, besitzt der Hochpunkt  von
von  die
die  _Koordinate
_Koordinate  Somit folgt
Somit folgt  Insgesamt besitzt das Parallelogramm damit einen Flächeninhalt von
Insgesamt besitzt das Parallelogramm damit einen Flächeninhalt von  Innenwinkel des Parallelogramms bestimmen
Innenwinkel des Parallelogramms bestimmen
 Für die Steigung dieser Tangente gilt somit
Für die Steigung dieser Tangente gilt somit  Da die obere und untere Seite des Parallelogramms parallel zur
Da die obere und untere Seite des Parallelogramms parallel zur  -Achse verlaufen, folgt somit für den rechten oberen Innenwinkel mit dem CAS:
-Achse verlaufen, folgt somit für den rechten oberen Innenwinkel mit dem CAS:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&m \\[5pt]
\tan(\alpha)&=&-6 \\[5pt]
\alpha&\approx&99,46^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/6c4038b2fe34b2a33d0e3ac8380c1393f081508f0a48119a1eb47bf2379ff871_light.svg) Die Größe des einen Innenwinkels beträgt somit ca.
Die Größe des einen Innenwinkels beträgt somit ca. 

Mit Hilfe des CAS folgt für die Funktionsgleichung der Tangente an  in beispielsweise
in beispielsweise 


c)
Verhältnis von  zeigen
Mit Hilfe der Nullstellen von
zeigen
Mit Hilfe der Nullstellen von  aus Aufgabenteil b) folgt durch Integrieren mit Hilfe des CAS für den Flächeninhalt der Fläche
aus Aufgabenteil b) folgt durch Integrieren mit Hilfe des CAS für den Flächeninhalt der Fläche 
 Für die Schnittstellen des Graphen von
Für die Schnittstellen des Graphen von  mit dem Graphen von
mit dem Graphen von  an denen
an denen  gilt, folgt mit dem solve-Befehl des CAS:
gilt, folgt mit dem solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
x_1&=&-\sqrt{2} \\[5pt]
x_2&=&0 \\[5pt]
x_3&=&\sqrt{2}
\end{array}\)](https://www.schullv.de/resources/formulas/f31708d104f3eccacc517259817cfb759ef8a773124a7fb9b4f080ec49bc8c36_light.svg) Von diesen Schnittstellen liegt nur
Von diesen Schnittstellen liegt nur  im I. Quadranten und ist somit die gesuchte Schnittstelle der beiden Graphen.
Der Flächeninhalt der Teilfläche zwischen
im I. Quadranten und ist somit die gesuchte Schnittstelle der beiden Graphen.
Der Flächeninhalt der Teilfläche zwischen  und
und  ergibt sich somit mit Hilfe des CAS wie folgt:
ergibt sich somit mit Hilfe des CAS wie folgt:
![\(\begin{array}[t]{rll}
A_1&=&\displaystyle\int_{0}^{\sqrt{2}}(f(x)-g_1(x))\;\mathrm dx \\[5pt]
&=&1\;[\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/a6d6fd85885fb3f6b15390ac306eb18a9399cf88ccaee0fa8c7e433dd2226152_light.svg) Für den Flächeninhalt der unteren Teilfläche folgt somit:
Für den Flächeninhalt der unteren Teilfläche folgt somit:
![\(A_2=A_A-A_1=1,25\;[\text{FE}]\)](https://www.schullv.de/resources/formulas/35934ef6b98a4c7631de821a031d30cf2e7c839cc5bd2737567ad954ad76fdcb_light.svg) Für das Verhältnis der Teilflächen gilt damit:
Für das Verhältnis der Teilflächen gilt damit:
 Wert für
Wert für  bestimmen
Mit Hilfe des Flächeninhalts der Fläche
bestimmen
Mit Hilfe des Flächeninhalts der Fläche  folgt, dass beide Teilfächen
folgt, dass beide Teilfächen ![\(\frac{1}{2}\cdot2,25=1,125\;[\text{FE}]\)](https://www.schullv.de/resources/formulas/ee6f2fb0cb78fa216f6155d1398510ba6e401d405e84be4fdb69be91e24e0d90_light.svg) groß sein müssen. Für die Schnittpunkte von
groß sein müssen. Für die Schnittpunkte von  und
und  folgt mit Hilfe des solve-Befehls des CAS:
folgt mit Hilfe des solve-Befehls des CAS:
 im I. Quadranten befinden. Damit die beiden Teilflächen gleichgroß sind, muss also folgende Gleichung gelten:
im I. Quadranten befinden. Damit die beiden Teilflächen gleichgroß sind, muss also folgende Gleichung gelten:
 Mit dem solve-Befehl des CAS folgt damit für
Mit dem solve-Befehl des CAS folgt damit für 
![\(\begin{array}[t]{rll}
m_1&\approx&0,88 \\[5pt]
m_2&\approx&-5,12
\end{array}\)](https://www.schullv.de/resources/formulas/00c49098f3bf6d25008863a161c23d3e8f64101138fa443e81f92fe0da6fe613_light.svg)
 Sowohl
Sowohl  als auch
als auch  erfüllen die Bedingung
erfüllen die Bedingung  allerdings verläuft
allerdings verläuft  für
für  bei positiven
bei positiven  -Werten komplett unterhalb der
-Werten komplett unterhalb der  -Achse, sodass der Schnittpunkt mit
-Achse, sodass der Schnittpunkt mit  nicht im I. Quadranten liegen kann. Die Gerade
nicht im I. Quadranten liegen kann. Die Gerade  teilt die Fläche
teilt die Fläche  somit für den Wert
somit für den Wert  in zwei gleich große Flächen.
in zwei gleich große Flächen.
falls
falls

d)
Mit Hilfe des solve-Befehls des CAS folgt für die Lösungen der Gleichung 
![\(\begin{array}[t]{rll}
x_1&\approx&-1,89 \\[5pt]
x_2&\approx&0,39 \\[5pt]
x_3&\approx&1,51
\end{array}\)](https://www.schullv.de/resources/formulas/4cfdb02ba96bca4cd7777808cdae56e90d88b09a0020bd329a000af24989a2fc_light.svg) Von diesen Lösungen liegen nur die zu
Von diesen Lösungen liegen nur die zu  und
und  gehörenden Funktionswerte im betrachteten I. Quadranten.
Damit ein Quadrat mit der Seitenlänge
gehörenden Funktionswerte im betrachteten I. Quadranten.
Damit ein Quadrat mit der Seitenlänge  in die Fläche passt, muss der Abstand zwischen
in die Fläche passt, muss der Abstand zwischen  und
und  größer oder gleich
größer oder gleich  sein. Für die Differenz gilt:
sein. Für die Differenz gilt:
![\(x_3-x_2 \approx 1,12\gt1,1\;[\text{LE}]\)](https://www.schullv.de/resources/formulas/3c0d5d2617419f4973d7e78d5151646a3626cd6f24f6ebbed169de8f1ab981e3_light.svg) Es folgt, dass man ein Quadrat mit der Seitenlänge
Es folgt, dass man ein Quadrat mit der Seitenlänge  aus der betrachteten Fläche ausschneiden kann.
aus der betrachteten Fläche ausschneiden kann.
e)
Graphen von  beschreiben
Es gilt
beschreiben
Es gilt 
 das heißt die Graphen von
das heißt die Graphen von  gehen aus dem Graphen von
gehen aus dem Graphen von  durch eine Streckung bzw. Stauchung entlang der
durch eine Streckung bzw. Stauchung entlang der  -Achse hervor.
Werte von
-Achse hervor.
Werte von  für gleichschenkliges Dreieck berechnen
Da die Graphen von
für gleichschenkliges Dreieck berechnen
Da die Graphen von  durch Streckung bzw. Stauchung entlang der
durch Streckung bzw. Stauchung entlang der  -Achse aus dem Graphen von
-Achse aus dem Graphen von  hervorgehen, besitzen alle Funktionen dieselben Nullstellen wie
hervorgehen, besitzen alle Funktionen dieselben Nullstellen wie  das heißt nach Aufgabenteil b) lauten die beiden gesuchten Nullstellen
das heißt nach Aufgabenteil b) lauten die beiden gesuchten Nullstellen  und
und 
Zudem ergeben sich die jeweiligen Hochpunkte durch Streckung bzw. Stauchung mit entlang der
entlang der  -Achse aus dem von
-Achse aus dem von  das heißt sie besitzen nach Aufgabenteil b) die Koordinaten
das heißt sie besitzen nach Aufgabenteil b) die Koordinaten  Damit das Dreick aus den Punkten mit den Koordinaten
Damit das Dreick aus den Punkten mit den Koordinaten  und
und  gleichschenklig ist, müssen mindestens zwei Seiten gleichlang sein.
gleichschenklig ist, müssen mindestens zwei Seiten gleichlang sein.
 Da die Strecke
Da die Strecke  auf der
auf der  -Achse verläuft und der
-Achse verläuft und der  -Wert von
-Wert von  für alle
für alle  nicht in der Mitte dieser Strecke liegt, wie in der Skizze für
nicht in der Mitte dieser Strecke liegt, wie in der Skizze für  verdeutlicht, kann
verdeutlicht, kann  für kein
für kein  gelten.
Die Länge der Seite
gelten.
Die Länge der Seite  ergibt sich als
ergibt sich als ![\(\left\vert\overrightarrow{AB}\right\vert = 3\;[\text{LE}].\)](https://www.schullv.de/resources/formulas/d0c8073af4a295f67d766f8b428094e2187ba6469660f181bd12a4da1e5c472a_light.svg) Für
Für ![\(\left\vert\overrightarrow{AH_k}\right\vert = 3\;[\text{LE}]\)](https://www.schullv.de/resources/formulas/204d1c578f9dc03fa4bba0e194417ff5407e0de6a3b820f7b3c2c28c5a65fe9c_light.svg) liefert der solve-Befehl des CAS:
liefert der solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
k_1&=&-\dfrac{\sqrt{2}}{2} \\[5pt]
k_2&=&\dfrac{\sqrt{2}}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/6c4c6d8b8ef7049958905d8a42a817fc3051850a83c049f8e9fe7270d4dda322_light.svg) Für die andere Möglichkeit,
Für die andere Möglichkeit, ![\(\left\vert\overrightarrow{BH_k}\right\vert = 3\;[\text{LE}],\)](https://www.schullv.de/resources/formulas/adb4000953a66e3eac0dfbabea7327070ec1d4e7887fa891c97e852b3c8d989f_light.svg) ergibt sich mit Hilfe des solve-Befehls des CAS:
ergibt sich mit Hilfe des solve-Befehls des CAS:
![\(\begin{array}[t]{rll}
k_3&=&-\dfrac{\sqrt{2\cdot\sqrt{3}-1}}{2} \\[5pt]
k_4&=&\dfrac{\sqrt{2\cdot\sqrt{3}-1}}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/3ed5a97c472255f6a539b3adea2833ef1504d39270e8923654ea857fbcb0c94e_light.svg) Da
Da  laut Aufgabenstellung eine positive reelle Zahl ist, ist das betrachtete Dreieck nur für die Werte
laut Aufgabenstellung eine positive reelle Zahl ist, ist das betrachtete Dreieck nur für die Werte  und
und  gleichschenklig.
gleichschenklig.
Zudem ergeben sich die jeweiligen Hochpunkte durch Streckung bzw. Stauchung mit
