Teil B3 - Stochastik

Johanna studiert Lehramt und untersucht im Rahmen ihrer Examensarbeit, inwieweit sich Thüringer Jugendliche im Alter von 12 bis 17 Jahren für Weltgeschehen, Klimawandel und Diversität interessieren.
Als Grundlage nutzt sie die Ergebnisse einer deutschlandweiten Befragung, deren Ergebnisse sie auf die Thüringer Jugendlichen überträgt.

Johanna plant eine Befragung mit $118$ Jugendlichen im Alter von 12 bis 13 Jahren und $132$ Jugendlichen im Alter von 16 bis 17 Jahren. Für ihre Prognose verwendet sie das Modell der Binomialverteilung und interpretiert die relativen Häufigkeiten der deutschlandweiten Studie als Wahrscheinlichkeiten.

Berechne die Wahrscheinlichkeiten der Ereignisse $A$ und $B.$

$A:$

„Genau $60$ der 12- bis 13-Jährigen interessieren sich für Diversität.“

$B:$

„Mindestens die Hälfte der 16- bis 17-Jährigen interessiert sich für Diversität.“

(4 BE)

Von den 16- bis 17-Jährigen gaben $110$ an, sich für Weltgeschehen zu interessieren. Johanna stellt folgende Rechnung auf:

$\begin{array}{ll} (\text{I})\quad&132\cdot 0,73 \approx 96 \\ (\text{II})\quad&\sqrt{132\cdot 0,73\cdot 0,27}\approx 5 \\ (\text{III})\quad&110\notin [86; 106] \\ \end{array}$

Interpretiere die einzelnen Schritte und formuliere daraus eine mögliche Schlussfolgerung für Johanna im Sachzusammenhang.

(5 BE)

Von den 12- bis 13-Jährigen gaben $74$ Jugendliche an, sich für den Klimawandel zu interessieren.
Beurteile mithilfe eines $95\,\text{%}$ -Konfidenzintervalls die Verträglichkeit dieses Umfrageergebnisses der 12- bis 13-Jährigen mit dem Ergebnis der deutschlandweiten Befragung.

Auch von den 16- bis 17-Jährigen gaben $74$ Jugendliche an, sich für den Klimawandel zu interessieren.
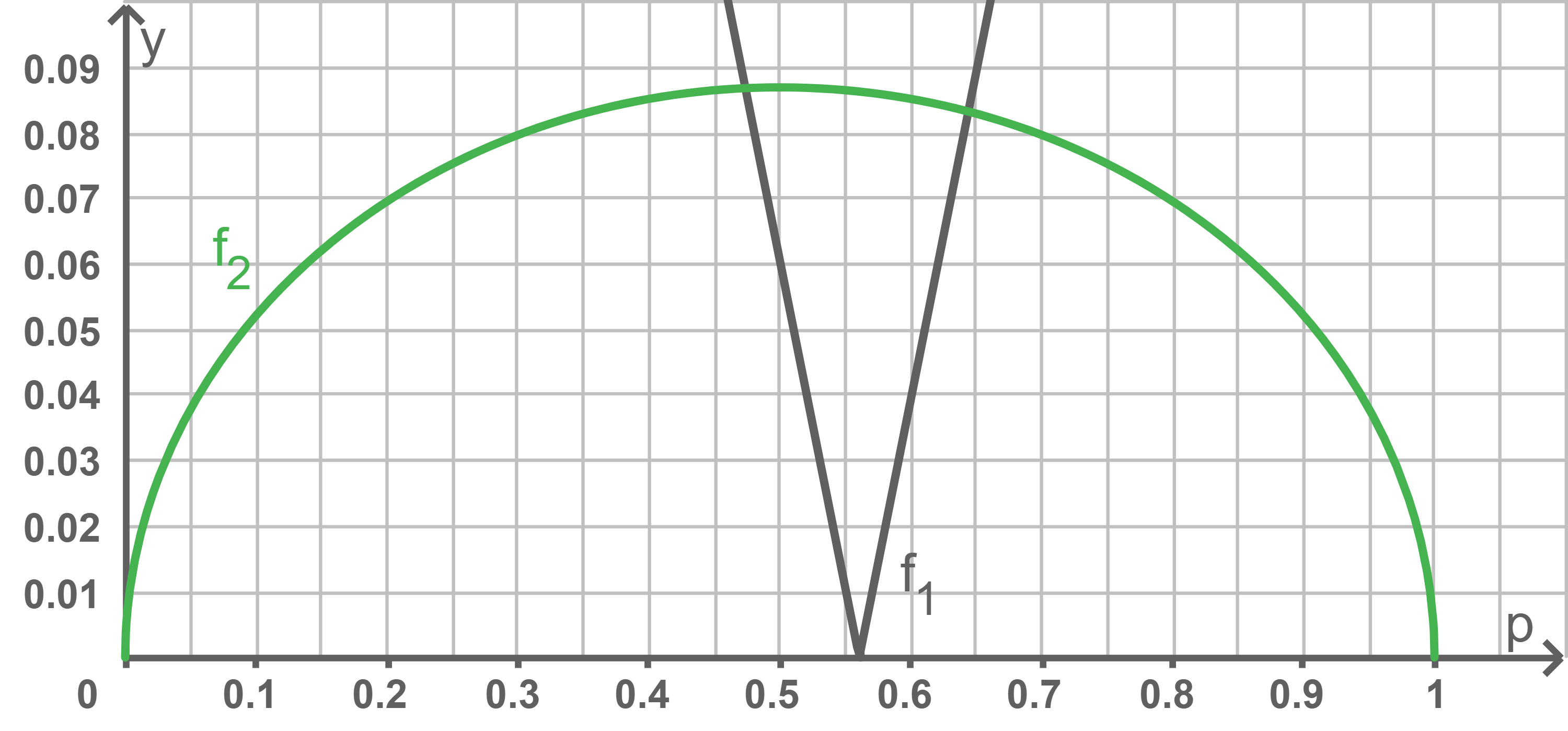
Beurteile die Verträglichkeit dieses Umfrageergebnisses der 16- bis 17-Jährigen mit dem Ergebnis der deutschlandweiten Befragung nur unter Verwendung der Graphen der Funktionen $f_1$ und $f_2.$ (siehe Abbildung)

$f_1(p)= \left\vert \dfrac{74}{132}-p \right\vert\quad$ $f_2(p)= \left\vert 2\cdot \sqrt{\dfrac{p\cdot (1-p)}{132}}\right\vert$

(6 BE)

Durch Beobachtung des Wetters über einen langen Zeitraum kann auf einen Klimawandel geschlussfolgert werden. Es wird die mittlere Tagestemperatur an einem Ort in Grad Celsius erfasst. Betrachtet werden die Daten einer Wetterstation in einem Zeitraum von 30 Jahren. Die mittlere Temperatur eines Augusttages im Zeitraum von 1991 bis 2020 wird durch die normalverteilte Zufallsgröße $X$ mit den Parametern $\mu = 18,1$ und $\sigma = 2,4$ beschrieben. Tage werden als extrem warm bezeichnet, wenn deren mittlere Tagestemperatur mindestens $22\;^\circ\text{C}$ beträgt.

Gib die Wahrscheinlichkeit $P(X \lt 22)$ und deren Bedeutung im Sachzusammenhang an.

(2 BE)

Ein Klimamodell prognostiziert für den Zeitraum von 2021 bis 2050 eine Verdreifachung der Wahrscheinlichkeit für einen extrem warmen Tag im August bezogen auf den Zeitraum von 1991 bis 2020.
Bestimme den Erwartungswert für die prognostizierte mittlere Tagestemperatur unter der Annahme, dass die Standardabweichung konstant bleibt.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Zufallsvariable $X$ gibt die Anzahl der befragten Personen in der jeweiligen Altersgruppe an, die sich für Diversität interessieren und ist binomialverteilt mit $n=118$ bzw. $n=132$ und $p=0,52$ bzw. $p=0,45.$ Somit folgt:

$\begin{array}[t]{rlll} P(A)&=&B_{118;0,52}(X=60) \\[5pt] &\approx&0,0710 \\[5pt] &=&7,1\,\% \end{array}$

$\begin{array}[t]{rlll} P(B)&=&B_{132;0,45}(X\geq66) \\[5pt] &\approx&0,1430 \\[5pt] &=&14,3\,\% \end{array}$

Schritt $(\text{I})$ berechnet den Erwartungswertfür die Anzahl an 16- bis 17-Jährigen, die sich für das Weltgeschehen interessieren. In Schritt $(\text{II})$ wird die zugehörige Standardabweichung bestimmt. Schritt $(\text{III})$ zeigt, dass der Wert von $110$ bei Johannas Befragung nicht im Prognoseintervall zur Sicherheitswahrscheinlichkeit von $95\,\%$ liegt.
Johanna sollte somit anzweifeln, ob sie die Angabe der deutschlandweiten Befragung bezüglich des Weltgeschehens der 16- bis 17-Jährigen auf ihre Stichprobe zur Sicherheitswahrscheinlichkeit von $95\,\%$ übertragen kann.

Verträglichkeit für 12- bis 13-Jährige beurteilen

Mit Hilfe der gegebenen Wert ergibt sich folgende Gleichung bezüglich des $95\,\%$ -Konfidenzintervalls:

$\left\vert\dfrac{74}{118}-p\right\vert \leq 2 \cdot \sqrt{\dfrac{p \cdot(1-p)}{118}}$

Auflösen mit dem CAS liefert das $95\,\%$ -Konfidenzintervall $[0,54;0,71].$ Da $0,58$ in diesem Intervall liegt, sind die Umfrageergebnisse somit verträglich mit dem Ergebnis der deutschlandweiten Befragung.

Verträglichkeit für 16- bis 17-Jährige beurteilen

Die Schnittstellen der Graphen entsprechen den Intervallgrenzen des $95\,\%$ -Konfidenzintervalls für $h=\frac{74}{132}.$ Da $0,66$ rechts von der oberen Intervallgrenze liegt, ist das Umfrageergebnis somit nicht mit der deutschlandweiten Befragung verträglich.

Wahrscheinlichkeit angeben

$P(X\lt22)\approx0,9479=94,79\,\%$

Bedeutung im Sachzusammenhang angeben

Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Tag nicht als extrem warm bezeichnet wird, beträgt $94,79\,\%.$

Aus der Aufgabenstellung ergibt sich folgende Gleichung, wenn $\(\mu$ der gesuchte neue Erwartungswert ist:

$\(3\cdot N_{18,1;2,4}(X\gt22)=N_{\mu$

Mit dem solve-Befehl des CAS ergibt sich $\(\mu$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?