Teil C2
1
Auf einem ebenen Gelände befindet sich ein  hoher Antennenmast. Dieses Gelände wird durch die
hoher Antennenmast. Dieses Gelände wird durch die  -Ebene eines Koordinatensystems dargestellt. Der Punkt
-Ebene eines Koordinatensystems dargestellt. Der Punkt  beschreibt den Fußpunkt des Antennenmastes. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
beschreibt den Fußpunkt des Antennenmastes. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
Zu einem bestimmten Zeitpunkt verlaufen die Sonnenstrahlen in Richtung des Vektors Sie erzeugen auf dem Boden einen Schatten des Antennenmastes.
Sie erzeugen auf dem Boden einen Schatten des Antennenmastes.
 beschrieben werden. Es soll untersucht werden, ob sich die Pflanze zu dem bestimmten Zeitpunkt im Schatten des Antennenmastes befindet.
beschrieben werden. Es soll untersucht werden, ob sich die Pflanze zu dem bestimmten Zeitpunkt im Schatten des Antennenmastes befindet.
Zu einem bestimmten Zeitpunkt verlaufen die Sonnenstrahlen in Richtung des Vektors
a)
Die Gerade  beschreibt den Verlauf des Lichtstrahles, der auf die Spitze des Antennenmastes trifft.
beschreibt den Verlauf des Lichtstrahles, der auf die Spitze des Antennenmastes trifft.
Gib eine Gleichung für an.
an.
Gib eine Gleichung für
(1 BE)
b)
Berechne die Koordinaten des Durchstoßpunktes  von
von  mit der
mit der  -Ebene sowie die Länge des Schattens in Metern.
-Ebene sowie die Länge des Schattens in Metern.
(2 BE)
c)
Bestimme die Größe des Winkels, unter dem das Licht auf den Boden fällt.
Eine kleine Pflanze wächst in der Nähe des Antennenmastes. Ihr Standort kann im Koordinatensystem durch den Punkt
(1 BE)
d)
Beurteile dazu die beiden folgenden Lösungsansätze:
(A)
Der Abstand zwischen Pflanze und Antennenmast wird berechnet und das Ergebnis wird mit der Schattenlänge des Antennenmastes verglichen.
(B)
Die Gleichung der Geraden durch die Punkte  und
und  wird aufgestellt. Anschließend wird überprüft, ob der Punkt
wird aufgestellt. Anschließend wird überprüft, ob der Punkt  auf dieser Geraden liegt.
auf dieser Geraden liegt.
(3 BE)
e)
Gib an, ob sich die Pflanze im Schatten des Antennenmastes befindet.
(1 BE)
2
Seit einiger Zeit wird in Politik und Medien diskutiert, ob es sinnvoll ist, dass Kinder in der Schule die Schreibschrift erlernen. Die Position, dass durch Computer und Smartphone für Kinder der Umgang mit der Druckschrift Alltag ist, kaum dass sie das Alphabet kennen, steht der Ansicht gegenüber, dass das Schreiben mit der Hand kreative Prozesse unterstützt oder, wie Cornelia Funke poetisch ausdrückte: „Die Schreibschrift bringe die ‚Gedanken zum Fliegen.‘“
Ein IT-Unternehmen hat hierzu eine Studie in Auftrag gegeben, die folgende Ergebnisse lieferte:
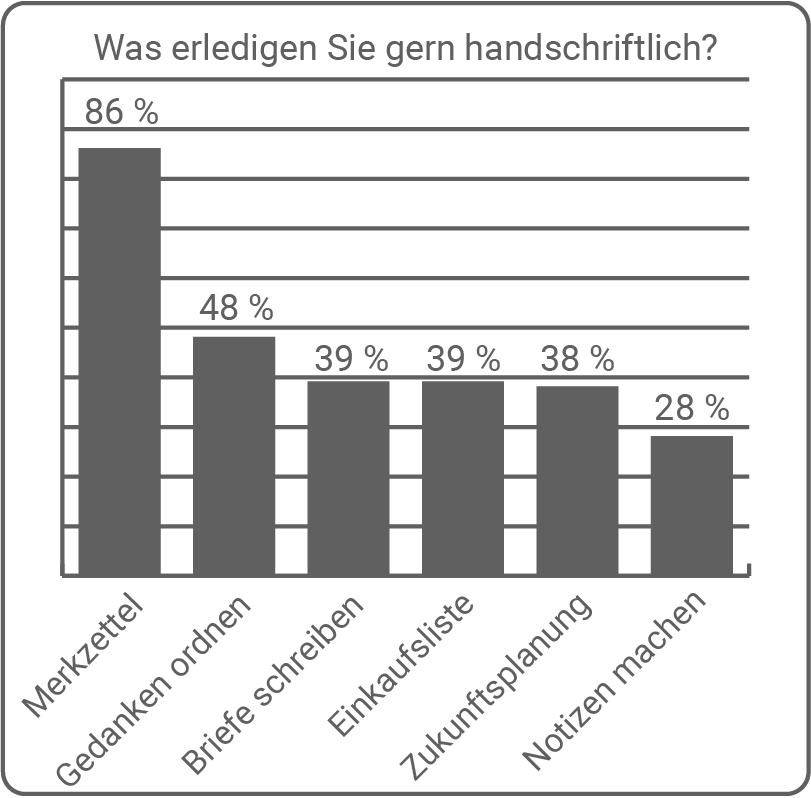
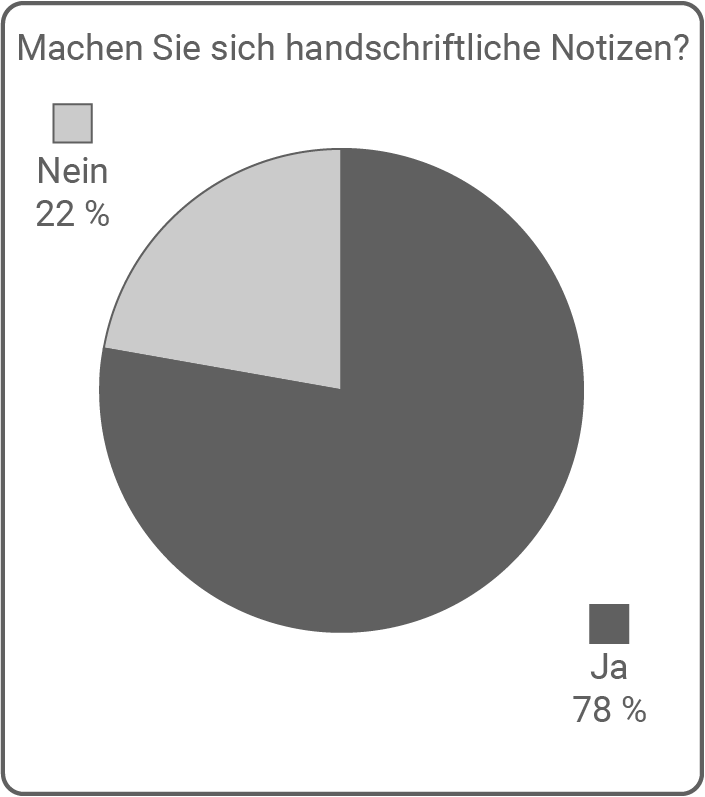

Nach: Rauch, Elena: Mehrheit überzeugt: Handschrift fördert Kreativität.
In Ostthüringer Zeitung. 21.05.2015.
In Ostthüringer Zeitung. 21.05.2015.

a)
Begründe, dass es nicht möglich ist, die Verteilung zur Frage „Was erledigen Sie gern handschriftlich?“ in einem Kreisdiagramm darzustellen.
(1 BE)
b)
Beschreibe unter Verwendung der obigen Statistik ein Ereignis  , dessen Wahrscheinlichkeit durch den Term
, dessen Wahrscheinlichkeit durch den Term  berechnet werden kann.
berechnet werden kann.
(2 BE)
c)
In einer Schule werden 96 Abiturienten befragt, was sie gern handschriftlich erledigen.
Berechne unter der Annahme des Modells der Binomialverteilung und unter Verwendung der obigen Statistik die Wahrscheinlichkeiten folgender Ereignisse:






„Genau 80 Abiturienten schreiben Merkzettel mit der Hand.“
„Mindestens 10 aber weniger als 80 Abiturienten schreiben Merkzettel mit der Hand.“
„Höchstens 40 Abiturienten ordnen ihre Gedanken handschriftlich.“
(3 BE)
d)
Ermittle die zu erwartende Anzahl unter den  Abiturienten, die handschriftlich Briefe schreiben.
Abiturienten, die handschriftlich Briefe schreiben.
Gib eine mögliche Ursache dafür an, dass dieses Ergebnis deinen Alltagsbeobachtungen widerspricht.
Bestimme die Wahrscheinlichkeit des Ereignisses:


Gib eine mögliche Ursache dafür an, dass dieses Ergebnis deinen Alltagsbeobachtungen widerspricht.
Bestimme die Wahrscheinlichkeit des Ereignisses:
„Die Anzahl der Abiturienten, die handschriftlich Briefe schreiben, weicht um höchstens fünf Abiturienten vom Erwartungswert ab.“
(3 BE)
e)
Die Frage „Machen Sie sich handschriftliche Notizen?“ wird vermutlich in zehn Jahren nur noch zu  mit „Ja“ beantwortet
mit „Ja“ beantwortet  statt der
statt der  aus dem Jahr 2015
aus dem Jahr 2015 
Konstruiere einen Alternativtest mit dem Stichprobenumfang der diese Hypothese zu höchstens
der diese Hypothese zu höchstens  zu Unrecht ablehnt.
zu Unrecht ablehnt.
Konstruiere einen Alternativtest mit dem Stichprobenumfang
(3 BE)
1.
a)
Die Mastspitze befindet sich  über
über  das heißt die
das heißt die  - und
- und  -Koordinaten der Spitze stimmen mit denen des Fußpunktes überein. Somit folgt für den Ortsvektor der Mastspitze:
-Koordinaten der Spitze stimmen mit denen des Fußpunktes überein. Somit folgt für den Ortsvektor der Mastspitze:
 Zusammen mit dem Richtungsvektor
Zusammen mit dem Richtungsvektor  aus der Aufgabenstellung ergibt sich für die gesuchte Geradengleichung:
aus der Aufgabenstellung ergibt sich für die gesuchte Geradengleichung:

b)
Koordinaten von  berechnen
Ein allgemeiner Punkt der
berechnen
Ein allgemeiner Punkt der  -Ebene hat die Koordinaten
-Ebene hat die Koordinaten  Gleichsetzen mit der Geradengleichung von
Gleichsetzen mit der Geradengleichung von  liefert folgendes Gleichungssystem:
liefert folgendes Gleichungssystem:
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
t&=&3 \\[5pt]
x&=&1 \\[5pt]
y&=&33
\end{array}\)](https://www.schullv.de/resources/formulas/5cf1dd6b5a933fc250193b3fef88b3419b3e6ff450f5dbb3b8655c378b3f69af_light.svg)
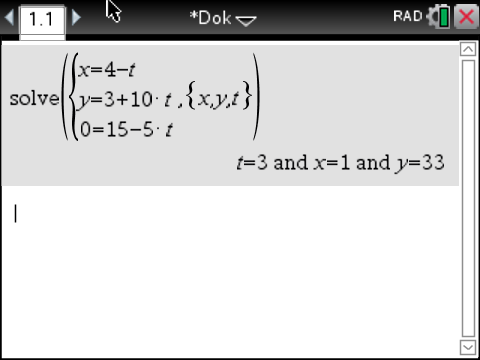 Der Durchstoßpunkt besitzt somit die Koordinaten
Der Durchstoßpunkt besitzt somit die Koordinaten  Länge des Schattens berechnen
Für den Vektor, der den Schatten beschreibt, ergibt sich:
Länge des Schattens berechnen
Für den Vektor, der den Schatten beschreibt, ergibt sich:
![\(\begin{array}[t]{rll}
\overrightarrow{FD}&=& \pmatrix{1\\33\\0}-\pmatrix{4\\3\\0} \\[5pt]
&=& \pmatrix{-3\\30\\0}
\end{array}\)](https://www.schullv.de/resources/formulas/d5030b2f14cbc66b89cbd2c4065e98dc54d26aa1c245b6131430f990492c8a68_light.svg) Mit Hilfe des CAS folgt nun für die Länge des Schattens:
Mit Hilfe des CAS folgt nun für die Länge des Schattens:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{FD}\right\vert&=&3\cdot\sqrt{101} \\[5pt]
&\approx&30,15\;[\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/fa20949f7b168ba1b62968b1ef7e2f66e42e7c45e7e01da00d04ec712b53148c_light.svg)



c)
Der Einfallswinkel  des Lichtes ergibt sich durch folgende Formel:
des Lichtes ergibt sich durch folgende Formel:
 Ein Normalenvektor der
Ein Normalenvektor der  -Ebene ist gegeben durch:
-Ebene ist gegeben durch:
 Einsetzen von
Einsetzen von  und
und  liefert mit Hilfe des CAS:
liefert mit Hilfe des CAS:
![\(\begin{array}[t]{rll}
\alpha&\approx&26,45^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/0d014335bca5553975c7471cfe03078214b3c68f3b742867ffede917d7b3530f_light.svg)
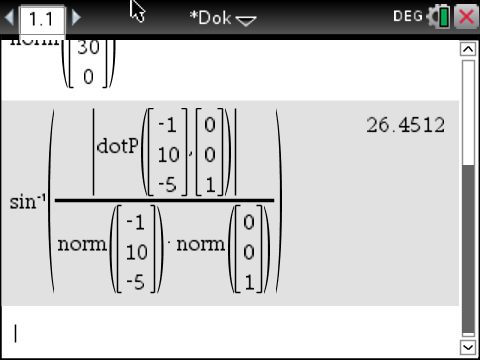 Das Licht fällt somit unter einem Winkel von ca.
Das Licht fällt somit unter einem Winkel von ca.  auf den Boden.
auf den Boden.

d)
Lösungsansatz (A) beurteilen
Lösungsansatz (A) ergibt keine hinreichende Überprüfung dafür, dass sich die Pflanze im Schatten des Antennenmastes befindet, denn der Schatten des Mastes verläuft in der Richtung des Vektors  In Ansatz (A) wird aber lediglich der Abstand zum Antennenmast betrachtet.
Lösungsansatz (B) beurteilen
Auch Lösungsansatz (B) ergibt keine hinreichende Überprüfung dafür, dass sich die Pflanze im Schatten des Antennenmastes befindet. Hier wird nur überprüft, ob die Pflanze in der gleichen Richtung wächst, in der auch der Schatten des Mastes verläuft. Da der Schatten allerdings nicht unbegrenzt lang ist, fehlt die Überprüfung des Abstandes der Pflanze zum Mast.
In Ansatz (A) wird aber lediglich der Abstand zum Antennenmast betrachtet.
Lösungsansatz (B) beurteilen
Auch Lösungsansatz (B) ergibt keine hinreichende Überprüfung dafür, dass sich die Pflanze im Schatten des Antennenmastes befindet. Hier wird nur überprüft, ob die Pflanze in der gleichen Richtung wächst, in der auch der Schatten des Mastes verläuft. Da der Schatten allerdings nicht unbegrenzt lang ist, fehlt die Überprüfung des Abstandes der Pflanze zum Mast.
e)
Damit sich die Pflanze im Schatten des Antennenmastes befindet, muss sie auf der Strecke  liegen. Die Gleichung
liegen. Die Gleichung  die dazu betrachtet wird, liefert folgendes Gleichungssystem:
die dazu betrachtet wird, liefert folgendes Gleichungssystem:
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
s&=&-0,5
\end{array}\)](https://www.schullv.de/resources/formulas/83c1305b9d3a194f8cb3790a36292e017a78f6871637086ab2aa40e791e26e08_light.svg) Da
Da ![\(s\notin[0;1]\)](https://www.schullv.de/resources/formulas/013390d161fe5cf3207c5b76b4b327a8aa2111ef275f2ba4ffa0a7557a765f27_light.svg) gilt, liegt die Pflanze nicht auf der Strecke
gilt, liegt die Pflanze nicht auf der Strecke  und befindet sich somit nicht im Schatten des Antennenmastes.
und befindet sich somit nicht im Schatten des Antennenmastes.
2.
a)
Eine Person kann z.B. sowohl einen Merkzettel als auch einen Brief gerne handschriftlich verfassen, das heißt Mehrfachnennungen sind möglich. Somit beträgt die Summe der Prozentsätze über  und ein Kreisdiagramm ist eher ungeeignet.
und ein Kreisdiagramm ist eher ungeeignet.
b)
Das Ereignis steht im Zusammenhang mit der im Kreisdiagramm dargestellten Statistik, da nur die beiden Wahrscheinlichkeiten  für die Antwortmöglichkeit „Ja“ und
für die Antwortmöglichkeit „Ja“ und  für die Antwortmöglichkeit „Nein“ vorkommen. Ein Vergleich mit der allgemeinen Schreibweise der Wahrscheinlichkeit eines binomialverteilten Ereignisses liefert als alternative Schreibweise des Terms:
für die Antwortmöglichkeit „Nein“ vorkommen. Ein Vergleich mit der allgemeinen Schreibweise der Wahrscheinlichkeit eines binomialverteilten Ereignisses liefert als alternative Schreibweise des Terms:

 Diese Gleichung verdeutlicht den Bezug zu einer binomialverteilten Zufallsgröße mit Parametern
Diese Gleichung verdeutlicht den Bezug zu einer binomialverteilten Zufallsgröße mit Parametern  und
und  Ein mögliches Ereignis
Ein mögliches Ereignis  ist somit gegeben durch:
„Von zehn zufällig ausgewählten Personen gaben mindestens neun an, sich handschriftliche Notizen zu machen“
ist somit gegeben durch:
„Von zehn zufällig ausgewählten Personen gaben mindestens neun an, sich handschriftliche Notizen zu machen“
c)
Die Zufallsgröße  beschreibt die Anzahl der Abiturienten, die Merkzettel mit der Hand schreiben, und ist binomialverteilt mit den Paramertern
beschreibt die Anzahl der Abiturienten, die Merkzettel mit der Hand schreiben, und ist binomialverteilt mit den Paramertern  und
und  Mit dem CAS folgt:
Mit dem CAS folgt:
![\(\begin{array}[t]{rll}
P(A)&=&B_{96;0,86}(X=80) \\[5pt]
&\approx&0,083 \\[5pt]
&=&8,3\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/ce4c5b90db924cea4630fa438ed65b1fadd47a263bd123a07858bd5969773f9e_light.svg)
![\(\begin{array}[t]{rll}
P(B)&=&B_{96;0,86}(10\leq X\leq79) \\[5pt]
&\approx&0,1820 \\[5pt]
&=&18,2\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/47884f289010223e787deb188a72ffa513da91dac8ce02d8d5ec8171b259db5c_light.svg) Die Zufallsgröße
Die Zufallsgröße  beschreibt die Anzahl der Abiturienten, die ihre Gedanken gerne handschriftlich ordnen, und ist binomialverteilt mit den Paramertern
beschreibt die Anzahl der Abiturienten, die ihre Gedanken gerne handschriftlich ordnen, und ist binomialverteilt mit den Paramertern  und
und  Mit dem CAS folgt somit für die Wahrscheinlichkeit von Ereignis
Mit dem CAS folgt somit für die Wahrscheinlichkeit von Ereignis 
![\(\begin{array}[t]{rll}
P(C)&=&B_{96;0,48}(Y\leq40) \\[5pt]
&\approx&0,1270 \\[5pt]
&=&12,7\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/bc71f3a5db15b7fe9ef95410bd9cd3d7e5b7aa692b618e3d51a8a34306141a0c_light.svg)
d)
Zu erwartende Anzahl ermitteln
Die zu erwartende Anzahl beträgt  und somit ca.
und somit ca.  Abiturienten.
Ursache angeben
Eine mögliche Ursache dafür, dass dieses Ergebnis den Alltagsbeobachtungen widerspricht ist, dass Briefe meist zu Hause geschrieben werden, wo es nur ein kleiner Teil der Allgemeinheit mitbekommt. Im Hinblick auf die größtenteils digitale Kommunikation lässt das dann darauf schließen, dass die Alltagsbeobachtung nicht der erwarteten Anzahl an Abiturienten entspricht.
Wahrscheinlichkeit bestimmen
Die Zufallsvariable
Abiturienten.
Ursache angeben
Eine mögliche Ursache dafür, dass dieses Ergebnis den Alltagsbeobachtungen widerspricht ist, dass Briefe meist zu Hause geschrieben werden, wo es nur ein kleiner Teil der Allgemeinheit mitbekommt. Im Hinblick auf die größtenteils digitale Kommunikation lässt das dann darauf schließen, dass die Alltagsbeobachtung nicht der erwarteten Anzahl an Abiturienten entspricht.
Wahrscheinlichkeit bestimmen
Die Zufallsvariable  gibt die Anzahl der Abiturienten an, die handschriftlich Briefe schreiben, und ist binomialverteilt mit den Parametern
gibt die Anzahl der Abiturienten an, die handschriftlich Briefe schreiben, und ist binomialverteilt mit den Parametern  und
und  Mit der eben berechneten zu erwarteten Anzahl ergibt sich mit Hilfe des CAS für die gesuchte Wahrscheinlichkeit:
Mit der eben berechneten zu erwarteten Anzahl ergibt sich mit Hilfe des CAS für die gesuchte Wahrscheinlichkeit:
e)
Der Alternativtest besitzt einen Stichprobenumfang von  ein Signifikanzniveau von
ein Signifikanzniveau von  eine Nullhypothese
eine Nullhypothese  mit
mit  und eine Alternativhypothese
und eine Alternativhypothese  mit
mit  Da
Da  gilt, hat der gesuchte Verwerfungsbereich somit folgende Form:
gilt, hat der gesuchte Verwerfungsbereich somit folgende Form:
 Die Zufallsvariable
Die Zufallsvariable  gibt die Anzahl der Befragten an, die sich handschriftliche Notizen machen, und ist binomialverteilt mit den Parametern
gibt die Anzahl der Befragten an, die sich handschriftliche Notizen machen, und ist binomialverteilt mit den Parametern  und
und  Für den gesuchten Test soll nun
Für den gesuchten Test soll nun  erfüllt sein. Systematisches Ausprobieren mit dem CAS liefert:
erfüllt sein. Systematisches Ausprobieren mit dem CAS liefert:

 Der Verwerfungsbereich ist somit gegeben durch
Der Verwerfungsbereich ist somit gegeben durch  das heißt die Nullhypothese des Tests wird abgelehnt, wenn mindestens
das heißt die Nullhypothese des Tests wird abgelehnt, wenn mindestens  der
der  Befragten angeben, handschriftliche Notizen zu machen.
Befragten angeben, handschriftliche Notizen zu machen.
1.
a)
Die Mastspitze befindet sich  über
über  das heißt die
das heißt die  - und
- und  -Koordinaten der Spitze stimmen mit denen des Fußpunktes überein. Somit folgt für den Ortsvektor der Mastspitze:
-Koordinaten der Spitze stimmen mit denen des Fußpunktes überein. Somit folgt für den Ortsvektor der Mastspitze:
 Zusammen mit dem Richtungsvektor
Zusammen mit dem Richtungsvektor  aus der Aufgabenstellung ergibt sich für die gesuchte Geradengleichung:
aus der Aufgabenstellung ergibt sich für die gesuchte Geradengleichung:

b)
Koordinaten von  berechnen
Ein allgemeiner Punkt der
berechnen
Ein allgemeiner Punkt der  -Ebene hat die Koordinaten
-Ebene hat die Koordinaten  Gleichsetzen mit der Geradengleichung von
Gleichsetzen mit der Geradengleichung von  liefert folgendes Gleichungssystem:
liefert folgendes Gleichungssystem:
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
t&=&3 \\[5pt]
x&=&1 \\[5pt]
y&=&33
\end{array}\)](https://www.schullv.de/resources/formulas/5cf1dd6b5a933fc250193b3fef88b3419b3e6ff450f5dbb3b8655c378b3f69af_light.svg)
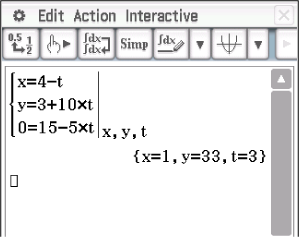 Der Durchstoßpunkt besitzt somit die Koordinaten
Der Durchstoßpunkt besitzt somit die Koordinaten  Länge des Schattens berechnen
Für den Vektor, der den Schatten beschreibt, ergibt sich:
Länge des Schattens berechnen
Für den Vektor, der den Schatten beschreibt, ergibt sich:
![\(\begin{array}[t]{rll}
\overrightarrow{FD}&=& \pmatrix{1\\33\\0}-\pmatrix{4\\3\\0} \\[5pt]
&=& \pmatrix{-3\\30\\0}
\end{array}\)](https://www.schullv.de/resources/formulas/d5030b2f14cbc66b89cbd2c4065e98dc54d26aa1c245b6131430f990492c8a68_light.svg) Mit Hilfe des CAS folgt nun für die Länge des Schattens:
Mit Hilfe des CAS folgt nun für die Länge des Schattens:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{FD}\right\vert&=&3\cdot\sqrt{101} \\[5pt]
&\approx&30,15\;[\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/fa20949f7b168ba1b62968b1ef7e2f66e42e7c45e7e01da00d04ec712b53148c_light.svg)
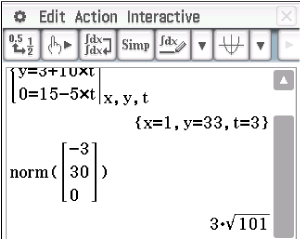


c)
Der Einfallswinkel  des Lichtes ergibt sich durch folgende Formel:
des Lichtes ergibt sich durch folgende Formel:
 Ein Normalenvektor der
Ein Normalenvektor der  -Ebene ist gegeben durch:
-Ebene ist gegeben durch:
 Einsetzen von
Einsetzen von  und
und  liefert mit Hilfe des CAS:
liefert mit Hilfe des CAS:
![\(\begin{array}[t]{rll}
\alpha&\approx&26,45^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/0d014335bca5553975c7471cfe03078214b3c68f3b742867ffede917d7b3530f_light.svg)
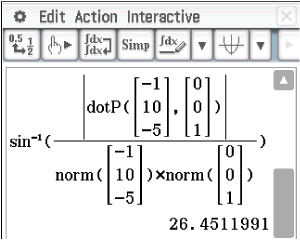 Das Licht fällt somit unter einem Winkel von ca.
Das Licht fällt somit unter einem Winkel von ca.  auf den Boden.
auf den Boden.

d)
Lösungsansatz (A) beurteilen
Lösungsansatz (A) ergibt keine hinreichende Überprüfung dafür, dass sich die Pflanze im Schatten des Antennenmastes befindet, denn der Schatten des Mastes verläuft in der Richtung des Vektors  In Ansatz (A) wird aber lediglich der Abstand zum Antennenmast betrachtet.
Lösungsansatz (B) beurteilen
Auch Lösungsansatz (B) ergibt keine hinreichende Überprüfung dafür, dass sich die Pflanze im Schatten des Antennenmastes befindet. Hier wird nur überprüft, ob die Pflanze in der gleichen Richtung wächst, in der auch der Schatten des Mastes verläuft. Da der Schatten allerdings nicht unbegrenzt lang ist, fehlt die Überprüfung des Abstandes der Pflanze zum Mast.
In Ansatz (A) wird aber lediglich der Abstand zum Antennenmast betrachtet.
Lösungsansatz (B) beurteilen
Auch Lösungsansatz (B) ergibt keine hinreichende Überprüfung dafür, dass sich die Pflanze im Schatten des Antennenmastes befindet. Hier wird nur überprüft, ob die Pflanze in der gleichen Richtung wächst, in der auch der Schatten des Mastes verläuft. Da der Schatten allerdings nicht unbegrenzt lang ist, fehlt die Überprüfung des Abstandes der Pflanze zum Mast.
e)
Damit sich die Pflanze im Schatten des Antennenmastes befindet, muss sie auf der Strecke  liegen. Die Gleichung
liegen. Die Gleichung  die dazu betrachtet wird, liefert folgendes Gleichungssystem:
die dazu betrachtet wird, liefert folgendes Gleichungssystem:
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
s&=&-0,5
\end{array}\)](https://www.schullv.de/resources/formulas/83c1305b9d3a194f8cb3790a36292e017a78f6871637086ab2aa40e791e26e08_light.svg) Da
Da ![\(s\notin[0;1]\)](https://www.schullv.de/resources/formulas/013390d161fe5cf3207c5b76b4b327a8aa2111ef275f2ba4ffa0a7557a765f27_light.svg) gilt, liegt die Pflanze nicht auf der Strecke
gilt, liegt die Pflanze nicht auf der Strecke  und befindet sich somit nicht im Schatten des Antennenmastes.
und befindet sich somit nicht im Schatten des Antennenmastes.
2.
a)
Eine Person kann z.B. sowohl einen Merkzettel als auch einen Brief gerne handschriftlich verfassen, das heißt Mehrfachnennungen sind möglich. Somit beträgt die Summe der Prozentsätze über  und ein Kreisdiagramm ist eher ungeeignet.
und ein Kreisdiagramm ist eher ungeeignet.
b)
Das Ereignis steht im Zusammenhang mit der im Kreisdiagramm dargestellten Statistik, da nur die beiden Wahrscheinlichkeiten  für die Antwortmöglichkeit „Ja“ und
für die Antwortmöglichkeit „Ja“ und  für die Antwortmöglichkeit „Nein“ vorkommen. Ein Vergleich mit der allgemeinen Schreibweise der Wahrscheinlichkeit eines binomialverteilten Ereignisses liefert als alternative Schreibweise des Terms:
für die Antwortmöglichkeit „Nein“ vorkommen. Ein Vergleich mit der allgemeinen Schreibweise der Wahrscheinlichkeit eines binomialverteilten Ereignisses liefert als alternative Schreibweise des Terms:

 Diese Gleichung verdeutlicht den Bezug zu einer binomialverteilten Zufallsgröße mit Parametern
Diese Gleichung verdeutlicht den Bezug zu einer binomialverteilten Zufallsgröße mit Parametern  und
und  Ein mögliches Ereignis
Ein mögliches Ereignis  ist somit gegeben durch:
„Von zehn zufällig ausgewählten Personen gaben mindestens neun an, sich handschriftliche Notizen zu machen“
ist somit gegeben durch:
„Von zehn zufällig ausgewählten Personen gaben mindestens neun an, sich handschriftliche Notizen zu machen“
c)
Die Zufallsgröße  beschreibt die Anzahl der Abiturienten, die Merkzettel mit der Hand schreiben, und ist binomialverteilt mit den Paramertern
beschreibt die Anzahl der Abiturienten, die Merkzettel mit der Hand schreiben, und ist binomialverteilt mit den Paramertern  und
und  Mit dem CAS folgt:
Mit dem CAS folgt:
![\(\begin{array}[t]{rll}
P(A)&=&B_{96;0,86}(X=80) \\[5pt]
&\approx&0,083 \\[5pt]
&=&8,3\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/ce4c5b90db924cea4630fa438ed65b1fadd47a263bd123a07858bd5969773f9e_light.svg)
![\(\begin{array}[t]{rll}
P(B)&=&B_{96;0,86}(10\leq X\leq79) \\[5pt]
&\approx&0,1820 \\[5pt]
&=&18,2\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/47884f289010223e787deb188a72ffa513da91dac8ce02d8d5ec8171b259db5c_light.svg) Die Zufallsgröße
Die Zufallsgröße  beschreibt die Anzahl der Abiturienten, die ihre Gedanken gerne handschriftlich ordnen, und ist binomialverteilt mit den Paramertern
beschreibt die Anzahl der Abiturienten, die ihre Gedanken gerne handschriftlich ordnen, und ist binomialverteilt mit den Paramertern  und
und  Mit dem CAS folgt somit für die Wahrscheinlichkeit von Ereignis
Mit dem CAS folgt somit für die Wahrscheinlichkeit von Ereignis 
![\(\begin{array}[t]{rll}
P(C)&=&B_{96;0,48}(Y\leq40) \\[5pt]
&\approx&0,1270 \\[5pt]
&=&12,7\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/bc71f3a5db15b7fe9ef95410bd9cd3d7e5b7aa692b618e3d51a8a34306141a0c_light.svg)
d)
Zu erwartende Anzahl ermitteln
Die zu erwartende Anzahl beträgt  und somit ca.
und somit ca.  Abiturienten.
Ursache angeben
Eine mögliche Ursache dafür, dass dieses Ergebnis den Alltagsbeobachtungen widerspricht ist, dass Briefe meist zu Hause geschrieben werden, wo es nur ein kleiner Teil der Allgemeinheit mitbekommt. Im Hinblick auf die größtenteils digitale Kommunikation lässt das dann darauf schließen, dass die Alltagsbeobachtung nicht der erwarteten Anzahl an Abiturienten entspricht.
Wahrscheinlichkeit bestimmen
Die Zufallsvariable
Abiturienten.
Ursache angeben
Eine mögliche Ursache dafür, dass dieses Ergebnis den Alltagsbeobachtungen widerspricht ist, dass Briefe meist zu Hause geschrieben werden, wo es nur ein kleiner Teil der Allgemeinheit mitbekommt. Im Hinblick auf die größtenteils digitale Kommunikation lässt das dann darauf schließen, dass die Alltagsbeobachtung nicht der erwarteten Anzahl an Abiturienten entspricht.
Wahrscheinlichkeit bestimmen
Die Zufallsvariable  gibt die Anzahl der Abiturienten an, die handschriftlich Briefe schreiben, und ist binomialverteilt mit den Parametern
gibt die Anzahl der Abiturienten an, die handschriftlich Briefe schreiben, und ist binomialverteilt mit den Parametern  und
und  Mit der eben berechneten zu erwarteten Anzahl ergibt sich mit Hilfe des CAS für die gesuchte Wahrscheinlichkeit:
Mit der eben berechneten zu erwarteten Anzahl ergibt sich mit Hilfe des CAS für die gesuchte Wahrscheinlichkeit:
e)
Der Alternativtest besitzt einen Stichprobenumfang von  ein Signifikanzniveau von
ein Signifikanzniveau von  eine Nullhypothese
eine Nullhypothese  mit
mit  und eine Alternativhypothese
und eine Alternativhypothese  mit
mit  Da
Da  gilt, hat der gesuchte Verwerfungsbereich somit folgende Form:
gilt, hat der gesuchte Verwerfungsbereich somit folgende Form:
 Die Zufallsvariable
Die Zufallsvariable  gibt die Anzahl der Befragten an, die sich handschriftliche Notizen machen, und ist binomialverteilt mit den Parametern
gibt die Anzahl der Befragten an, die sich handschriftliche Notizen machen, und ist binomialverteilt mit den Parametern  und
und  Für den gesuchten Test soll nun
Für den gesuchten Test soll nun  erfüllt sein. Systematisches Ausprobieren mit dem CAS liefert:
erfüllt sein. Systematisches Ausprobieren mit dem CAS liefert:

 Der Verwerfungsbereich ist somit gegeben durch
Der Verwerfungsbereich ist somit gegeben durch  das heißt die Nullhypothese des Tests wird abgelehnt, wenn mindestens
das heißt die Nullhypothese des Tests wird abgelehnt, wenn mindestens  der
der  Befragten angeben, handschriftliche Notizen zu machen.
Befragten angeben, handschriftliche Notizen zu machen.