Pflichtaufgaben
Funktionsgleichung von  |
Funktionsgleichung von  |
|---|---|
 |
|
 |
|
 |
|
 |
|
 |
Gegeben ist die in 
definierte Funktion 
mit 
Es gilt 
Zeige, dass 
eine Extremstelle von ist.
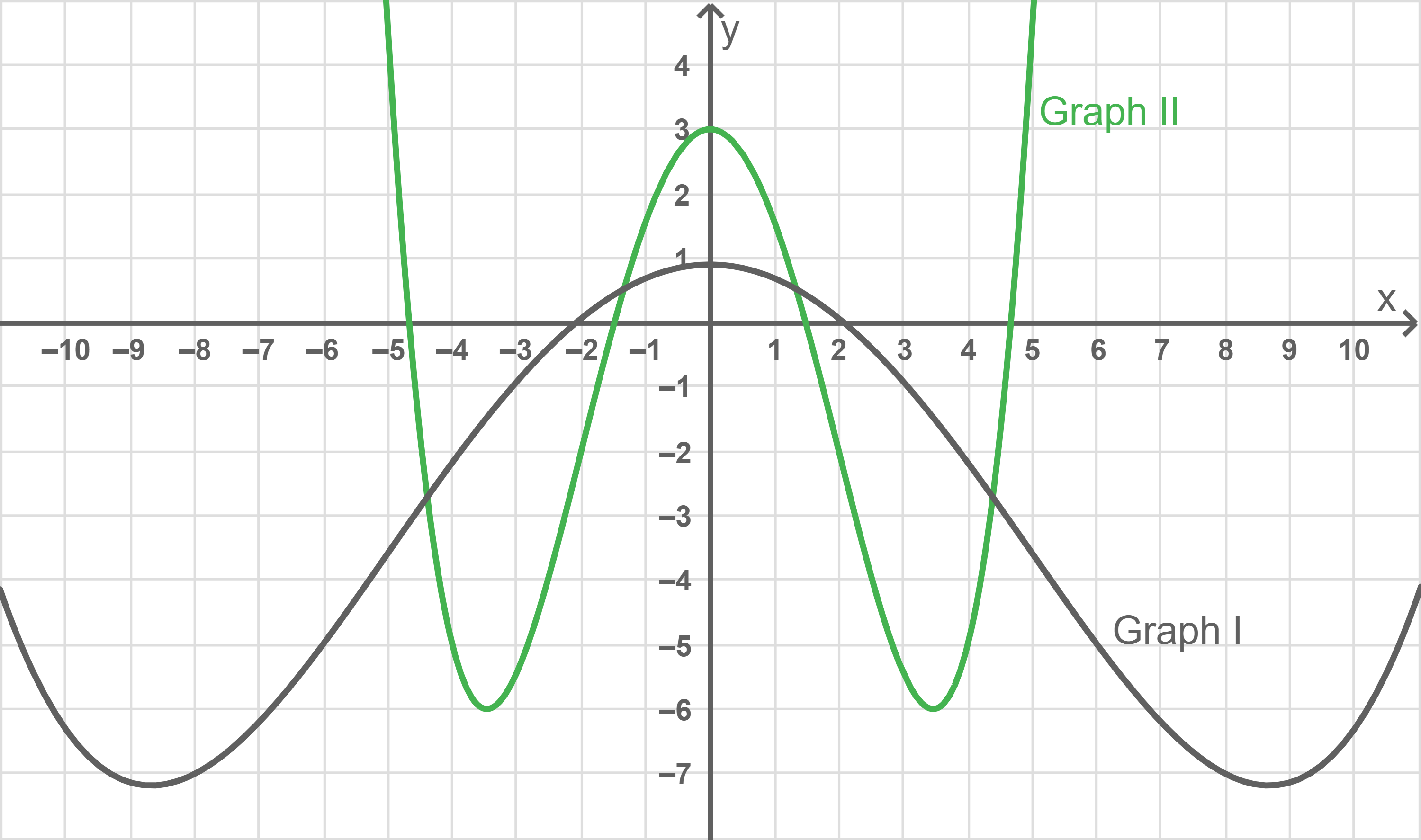
Einer der abgebildeten Graphen I und II ist der Graph einer Stammfunktion von 
Gib diesen Graphen an und begründe deine Angabe.
Die Abbildung zeigt einen Würfel 
der Kantenlänge 
in einem Koordinatensystem. Drei Seitenflächen dieses Würfels liegen in Koordinatenebenen. Die Ebene 
enthält die Punkte 
und den Mittelpunkt der Kante 
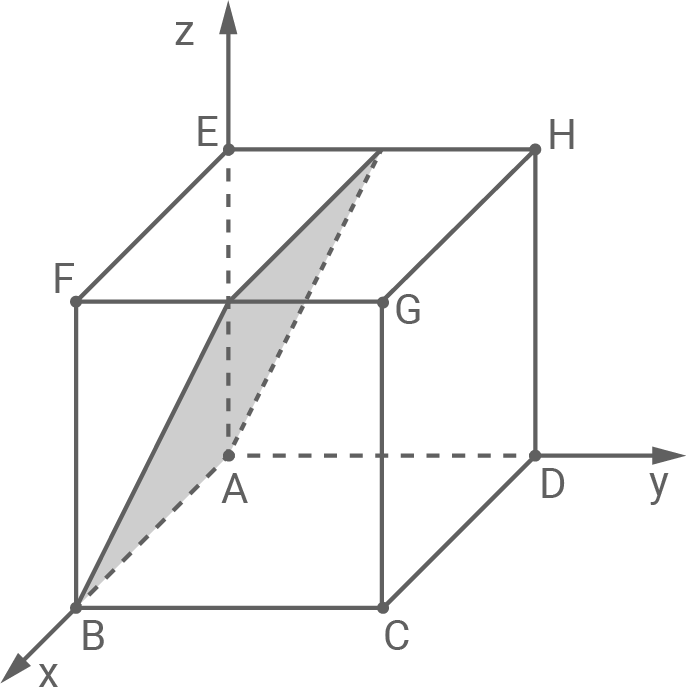
Die Ebene teilt den Würfel in zwei Teilkörper.
Berechne das Volumen des kleineren Teilkörpers.
Eine zweite Ebene 
enthält die Punkte 
und 
sowie den Mittelpunkt der Kante 
Zeichne die Schnittfigur dieser Ebene mit dem Würfel in die Abbildung ein und gib eine Gleichung der Schnittgerade der Ebenen und an.
Betrachtet wird die binomialverteilte Zufallsgröße 
mit den Parametern 
und 
Abbildung 1 zeigt die Wahrscheinlichkeitsverteilung von 
Entscheide, ob die folgende Aussage richtig ist, und begründe deine Entscheidung:
Betrachtet wird zudem die binomialverteilte Zufallsgröße 
mit den Parametern 
und 
Abbildung 2 zeigt die Wahrscheinlichkeitsverteilung von 
Die Erwartungswerte von und sind ganzzahlig und es gilt 
Weise unter Verwendung der Abbildungen 1 und 2 nach, dass 
gilt.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
Für die erste Ableitung von gilt:
![\(\begin{array}[t]{rlll}
f](https://www.schullv.de/resources/formulas/99e56acaa8282445519ae93d1f86702863d4ce101da2da223e6adfcaaf75d3c1_light.svg)
Einsetzen von 
liefert:
![\(\begin{array}[t]{rlll}
f](https://www.schullv.de/resources/formulas/a728329042414ce77cdbac65e27fc50f339f97497a87ed3188eec62ba0a4eec9_light.svg)
Somit ist die notwendige Bendingung für Extremstellen in erfüllt. Da die hinreichende Bedingung für Extremstellen bereits in der Aufgabenstellung gegeben ist, folgt somit, dass eine Extremstelle von ist.
Da bei eine Extremstelle besitzt, hat jede Stammfunktion von bei eine Wendestelle. Aus der Abbildung folgt somit, dass Graph II der Graph einer Stammfunktion von ist.
Da die Ebene die Kante 
und die zu dieser Kante parallelverlaufende Verbindungsstrecke zwischen den Mittelpunkten der Kanten 
und 
enthält (siehe Abbildung), halbiert sie eine Hälfte des Würfels 
Das Volumen des kleineren Teilkörpers macht somit insgesamt ein Viertel des Gesamtvolumens aus.
Aus den Koordinaten der Punkte 
und 
lässt sich direkt ablesen, dass die Länge der Kanten des Würfels 
beträgt. Damit folgt für das gesuchte Volumen des kleineren Teilkörpers:
Schnittfigur einzeichnen
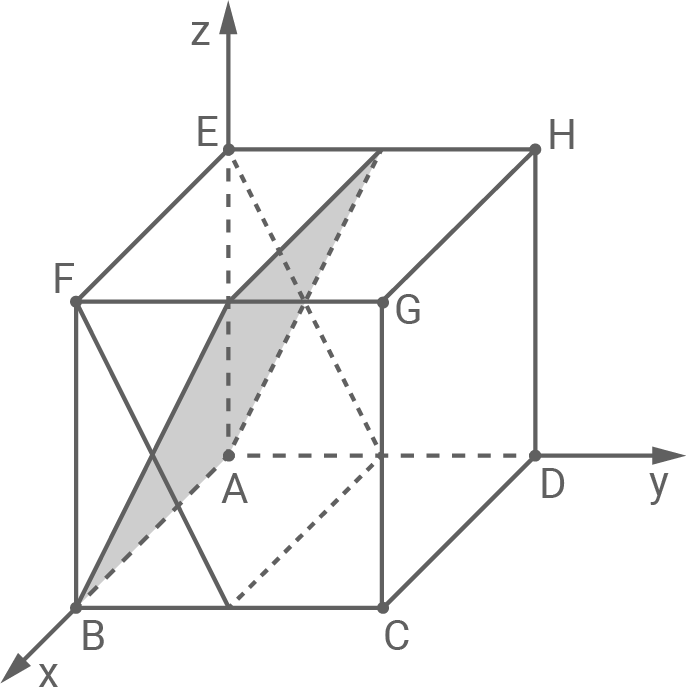
Gleichung der Schnittgeraden angeben
Anhand der Schnittfigur der Ebene mit dem Würfel lässt sich erkennen, dass die Schnittgerade der beiden Ebenen parallel zur 
-Achse verläuft und auf halber Höhe des Würfels liegt, d.h. alle Punkte der Geraden besitzen 
-Koordinate 
Anhand der Ähnlichkeit der beiden Ebenen folgt zudem, dass die 
-Koordinate der Punkte auf der Geraden konstant 
beträgt. Somit folgt als Geradengleichung der Schnittgeraden:
Die Abbildung zeigt, dass alle fünf Werte, die aufsummiert werden, jeweils kleiner als 
sind. Damit kann die Summe nicht größer als 
sein und die Aussage ist somit falsch.
Aus den beiden Abbildungen lässt sich erkennen, dass der Erwartungswert von genau 
beträgt und 
der Erwartungswert von Damit gilt also 
und 
Es folgt:
![\(\begin{array}[t]{rlll}
56&=&n_2\cdot p_2 \\[5pt]
4\cdot14&=&n_2\cdot p_2 \\[5pt]
4\cdot n_1\cdot p_1&=&n_2\cdot p_2
\end{array}\)](https://www.schullv.de/resources/formulas/b3dbae2cadfa0545b7d7aba795ee3caab1cb354d9de05dbce1f864cbc6df3295_light.svg)
Nach der Aufgabenstellung gilt 
Dividieren durch diesen Wert auf beiden Seiten liefert somit 