Teil B1
Die Profillinie einer Achterbahn wird abschnittsweise durch Funktionsgraphen modelliert. Für den letzten Abschnitt dieser Achterbahn mit anschließendem Anhaltebereich können die Graphen dreier Funktionen  ,
,  und
und  verwendet werden.
verwendet werden.
Die Werte

 und
und  stellen Maßzahlen zu Längenangaben in Metern dar.
stellen Maßzahlen zu Längenangaben in Metern dar.
Die Funktionen und
und  sind gegeben durch
sind gegeben durch

 und
und 
 Der Abschnitt der Achterbahn im Intervall
Der Abschnitt der Achterbahn im Intervall  wird durch den Graphen einer Funktion
wird durch den Graphen einer Funktion  beschrieben. Die Übergänge in den Randpunkten des Graphen von
beschrieben. Die Übergänge in den Randpunkten des Graphen von  sind ohne Knick zu realisieren.
sind ohne Knick zu realisieren.
Die Werte
Die Funktionen
a)
Stelle die Graphen von  und
und  in den angegebenen Intervallen in einem geeigneten Koordinatensystem graphisch dar.
in den angegebenen Intervallen in einem geeigneten Koordinatensystem graphisch dar.
Skizziere einen möglichen Verlauf des Graphen von .
.
Berechne die maximale Höhe der Achterbahn für
Berechne die Koordinaten des Punktes, in dem das Gefälle in diesem Intervall am größten ist.
Skizziere einen möglichen Verlauf des Graphen von
Berechne die maximale Höhe der Achterbahn für
Berechne die Koordinaten des Punktes, in dem das Gefälle in diesem Intervall am größten ist.
(6 BE)
b)
Im Punkt  trifft ein Sonnenstrahl senkrecht auf die Bahn. Dieser Sonnenstrahl schließt mit der Horizontalen einen Winkel ein.
trifft ein Sonnenstrahl senkrecht auf die Bahn. Dieser Sonnenstrahl schließt mit der Horizontalen einen Winkel ein.
Ermittle die Größe dieses Winkels.
Zu einem anderen Zeitpunkt treffen Sonnenstrahlen unter einem Winkel von zur Horizontalen auf die Bahn.
zur Horizontalen auf die Bahn.
Bestimme die Koordinaten der Punkte auf dem fallenden Bereich des Graphen von , in denen die Sonnenstrahlen senkrecht auf die Bahn treffen.
, in denen die Sonnenstrahlen senkrecht auf die Bahn treffen.
Ermittle die Größe dieses Winkels.
Zu einem anderen Zeitpunkt treffen Sonnenstrahlen unter einem Winkel von
Bestimme die Koordinaten der Punkte auf dem fallenden Bereich des Graphen von
(4 BE)
c)
Gesucht ist eine Gleichung für den Graphen von  , so dass der Graph die beschriebenen Eigenschaften besitzt.
, so dass der Graph die beschriebenen Eigenschaften besitzt.
Erläutere ein Vorgehen, um diese zu ermitteln. Gib eine mögliche Gleichung für an.
an.
Erläutere ein Vorgehen, um diese zu ermitteln. Gib eine mögliche Gleichung für
(4 BE)
d)
Eine mögliche Gleichung für  ist
ist

 Die Länge
Die Länge  eines Graphen einer Funktion
eines Graphen einer Funktion  im Intervall
im Intervall  kann mit der Gleichung
kann mit der Gleichung  berechnet werden. Für das Intervall
berechnet werden. Für das Intervall  wurde mit dieser Gleichung die Länge
wurde mit dieser Gleichung die Länge  ermittelt.
ermittelt.
Berechne die Länge der Bahn im Intervall .
.
Berechne die Länge der Bahn im Intervall
(3 BE)
e)
Um die aktuelle Geschwindigkeit der Wagen der Achterbahn anzuzeigen, sind diese jeweils mit einem Tachometer ausgerüstet. Mit Beginn des Bremsvorganges zeichnet ein Tachometer folgende Daten auf:
(Erst nach 10 Sekunden kommt der Wagen zum Stillstand.)
Ermittle eine Gleichung für eine Funktion  in Abhängigkeit von
in Abhängigkeit von  , die diesen Sachverhalt näherungsweise beschreibt.
, die diesen Sachverhalt näherungsweise beschreibt.
Bestimme den Flächeninhalt der Fläche zwischen dem Graphen der Funktion und der
und der  -Achse im Intervall
-Achse im Intervall  .
.
Interpretiere dieses Ergebnis im Zusammenhang mit dem Sachverhalt.
| Zeit |
Geschwindigkeit |
|---|---|
| 0 | 20 |
| 2 | 10 |
| 4 | 4 |
| 6 | 1,5 |
| 10 | 0 |
Bestimme den Flächeninhalt der Fläche zwischen dem Graphen der Funktion
Interpretiere dieses Ergebnis im Zusammenhang mit dem Sachverhalt.
(3 BE)
a)
Graphen von  und
und  darstellen
Der CAS liefert folgende graphische Darstellung der beiden Funktionen
darstellen
Der CAS liefert folgende graphische Darstellung der beiden Funktionen  und
und  sowie eine Wertetabelle für die beiden betrachteten Funktionen:
sowie eine Wertetabelle für die beiden betrachteten Funktionen:
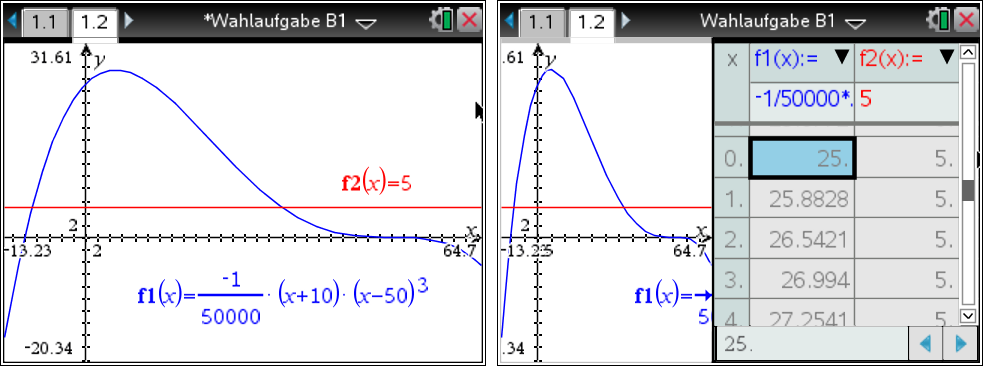 Unter Zuhilfenahme der Wertetabelle und Beachtung der in der Aufgabenstellung angegebenen Intervalle ergibt sich folgende Abbildung:
Unter Zuhilfenahme der Wertetabelle und Beachtung der in der Aufgabenstellung angegebenen Intervalle ergibt sich folgende Abbildung:
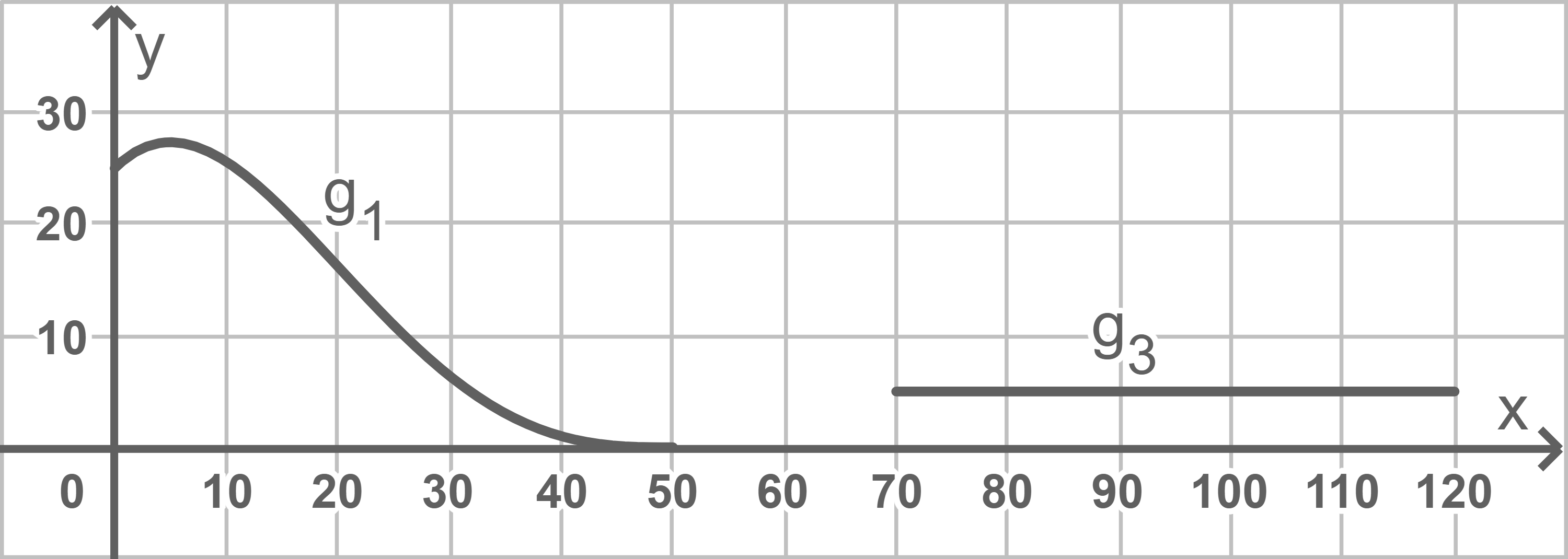 Möglichen Verlauf des Graphen von
Möglichen Verlauf des Graphen von  skizzieren
Der Graph der Funktion
skizzieren
Der Graph der Funktion  soll knickfrei in die beiden bereits eingezeichneten Graphen übergehen, somit ergibt sich ein möglicher Verlauf des Graphen von
soll knickfrei in die beiden bereits eingezeichneten Graphen übergehen, somit ergibt sich ein möglicher Verlauf des Graphen von  wie folgt:
wie folgt:
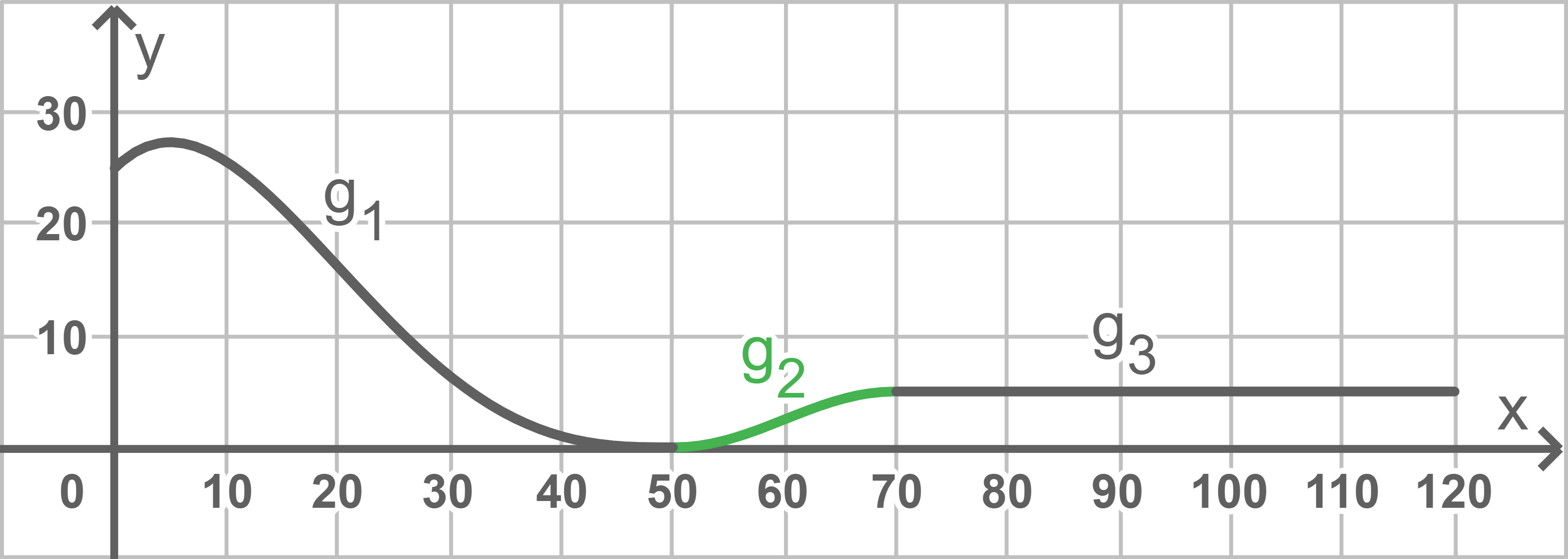 Maximale Höhe berechnen
Mit dem CAS folgt für die ersten beiden Ableitungen von
Maximale Höhe berechnen
Mit dem CAS folgt für die ersten beiden Ableitungen von 

 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&=&5 \\[5pt]
x_2&=&50
\end{array}\)](https://www.schullv.de/resources/formulas/cadb9159ed6e503885b973d085ac8696d7e08d5ff5f00a91ba55f4493e479523_light.svg)
 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
g_1](https://www.schullv.de/resources/formulas/5fe4f211c0ce489521f859d54274a47f19b1d59a9704ba437f0665480ae00fe2_light.svg)
 Dem Verlauf des Graphen von
Dem Verlauf des Graphen von  ist zu entnehmen, dass keine Randmaxima existieren. Somit besitzt der Graph von
ist zu entnehmen, dass keine Randmaxima existieren. Somit besitzt der Graph von  an der Stelle
an der Stelle  ein Hochpunkt. Einsetzen von
ein Hochpunkt. Einsetzen von  in
in  liefert die gesuchte maximale Höhe von
liefert die gesuchte maximale Höhe von ![\(g_1(5)\approx27,34\;[\text{m}].\)](https://www.schullv.de/resources/formulas/dcebbf46152157812bffebd9a3310a6f0cddc2360c74c40667929f290ea1fc57_light.svg) Punkt bestimmen, in dem Gefälle am größten ist
Mit dem CAS folgt für die dritte Ableitung von
Punkt bestimmen, in dem Gefälle am größten ist
Mit dem CAS folgt für die dritte Ableitung von 
 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_3&=&20 \\[5pt]
x_4&=&50
\end{array}\)](https://www.schullv.de/resources/formulas/e7ccdae4802d3c7e8a53c749de84ecaf46fcb2e942d6b4fd1ea4ffe9249b27e2_light.svg)
 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
g_1](https://www.schullv.de/resources/formulas/971e9839200799df099c854efaa4bf7034e11ef4a3a2eea309a6588f1fc7497c_light.svg)
 Dem Verlauf des Graphen von
Dem Verlauf des Graphen von  ist zu entnehmen, dass das Gefälle an der Stelle
ist zu entnehmen, dass das Gefälle an der Stelle  größer als an der Stelle
größer als an der Stelle  ist. Einsetzen von
ist. Einsetzen von  in
in  liefert
liefert  Die Koordinaten des Punktes
Die Koordinaten des Punktes  in dem das Gefälle in diesem Intervall am größten ist betragen somit
in dem das Gefälle in diesem Intervall am größten ist betragen somit 







b)
Größe des Winkels bestimmen
Mit dem CAS folgt für die Funktionsgleichung der Normalen im Punkt 
 Da die Normale eine Gerade ist, folgt aus der Funktionsgleichung direkt ihre Steigung von
Da die Normale eine Gerade ist, folgt aus der Funktionsgleichung direkt ihre Steigung von 
 Für den Winkel, den die Normale mit der
Für den Winkel, den die Normale mit der  -Achse einschließt, folgt somit mit dem CAS:
-Achse einschließt, folgt somit mit dem CAS:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&\dfrac{25}{27} \\[5pt]
\alpha&\approx&42,8^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/1b5fbc962eecda577011761a4e7662710a942178a437b6911ae56d06a4906f0a_light.svg) Koordinaten der Punkte bestimmen
Wenn die Sonnenstrahlen einen Winkel von
Koordinaten der Punkte bestimmen
Wenn die Sonnenstrahlen einen Winkel von  mit der Horizontalen einschließen, dann gilt für die Steigung
mit der Horizontalen einschließen, dann gilt für die Steigung  der Normalen an den Graphen
der Normalen an den Graphen  in diesem Punkt:
in diesem Punkt:
 Die Steigung der zugehörigen Tangente an
Die Steigung der zugehörigen Tangente an  und somit der Wert von
und somit der Wert von  an diesem Punkt beträgt damit
an diesem Punkt beträgt damit  Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&\approx&15,51 \\[5pt]
x_2&=&25 \\[5pt]
x_3&\approx&64,5
\end{array}\)](https://www.schullv.de/resources/formulas/c7c466c16b23749646cf2a9cd4bac736dca9c55ff4dae9ce0ac00b830385e739_light.svg) Da
Da ![\(x_3\notin[0;50]\)](https://www.schullv.de/resources/formulas/f636c3c008fa0e1d1cd359b5817e5580dc451ff67d05081676d71db6d8fd5e1b_light.svg) gilt, kommt dieser Wert nicht infrage.
gilt, kommt dieser Wert nicht infrage.
 Einsetzen von
Einsetzen von  und
und  in
in  liefert die Koordinaten
liefert die Koordinaten  und
und  der gesuchten Punkte.
der gesuchten Punkte.


c)
Damit der Graph von  knickfrei in die anderen beiden Graphen übergeht, müssen folgende Bedingungen gelten:
knickfrei in die anderen beiden Graphen übergeht, müssen folgende Bedingungen gelten:
![\(\begin{array}[t]{rll}
g_2(50)&=&g_1(50) \\[5pt]
g_2(70)&=&g_3(70) \\[5pt]
g_2](https://www.schullv.de/resources/formulas/6b0895d22650776b70a84b09e1eaadde1d195f174dc420e772c5908858ef8240_light.svg) Anhand des in Teilaufgabe a) skizzierten Graphen ist ersichtlich, dass
Anhand des in Teilaufgabe a) skizzierten Graphen ist ersichtlich, dass  weder eine lineare noch quadratische Funktion sein kann. Ein möglicher Ansatz ist nun, eine kubische Funktion
weder eine lineare noch quadratische Funktion sein kann. Ein möglicher Ansatz ist nun, eine kubische Funktion  zu konstruieren, das heißt
zu konstruieren, das heißt  und
und  sind der folgenden allgemeinen Formen:
sind der folgenden allgemeinen Formen:

 Mit dem CAS ergeben sich die Werte
Mit dem CAS ergeben sich die Werte 

 und
und  für die obigen Bedingungen. Zusammen mit den allgemeinen Funktionsgleichungen ergibt sich folgendes lineares Gleichungssystem:
für die obigen Bedingungen. Zusammen mit den allgemeinen Funktionsgleichungen ergibt sich folgendes lineares Gleichungssystem:
 Ein möglicher Funktionsterm von
Ein möglicher Funktionsterm von  ist somit gegeben durch
ist somit gegeben durch 

Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
a&=&-\dfrac{1}{800} \\[5pt]
b&=&\dfrac{9}{40} \\[5pt]
c&=&-\dfrac{105}{8} \\[5pt]
d&=&250
\end{array}\)](https://www.schullv.de/resources/formulas/e450c858b16a162c4819461d2af9551c79e04ab2be349e7cd3cc8084f4ba1c7f_light.svg)

d)
1. Schritt: Länge im Intervall ![\(\boldsymbol{[50;70]}\)](https://www.schullv.de/resources/formulas/27f88ad0df2ad5219770fd1f3edab56e49685f0317e1427988e82461c1be48fd_light.svg) berechnen
berechnen
 2. Schritt: Länge im Intervall
2. Schritt: Länge im Intervall ![\(\boldsymbol{[70;120]}\)](https://www.schullv.de/resources/formulas/6b78c0107a3dd91888cb09e302989d2547637d8449cc04bd4cf87a89f1047843_light.svg) berechnen
Im Intervall
berechnen
Im Intervall ![\([70;120]\)](https://www.schullv.de/resources/formulas/1638ab42ace7801b366bfb13ef3e0fc0af718a6118e3a3c1670431f3e25d5fa2_light.svg) wird die Bahn durch
wird die Bahn durch  beschrieben. Da
beschrieben. Da  konstant ist, ergibt sich die Länge der Bahn direkt als Differenz der Randstellen:
konstant ist, ergibt sich die Länge der Bahn direkt als Differenz der Randstellen:
![\(k_3=120-70=50\;[\text{m}]\)](https://www.schullv.de/resources/formulas/fb7f41311e71f24cad6561f3adf426ff53c4809678fc4e1586fadd64d7c9ce25_light.svg) 3. Schritt: Länge im Intervall
3. Schritt: Länge im Intervall ![\(\boldsymbol{[0;120]}\)](https://www.schullv.de/resources/formulas/164c9f69f1a0d652fe950b8e427cd3ac3e0ef38b6d80da86f7608767541b482c_light.svg) berechnen
Für die gesuchte Länge der Bahn folgt nun mit den berechneten Werten:
berechnen
Für die gesuchte Länge der Bahn folgt nun mit den berechneten Werten:
![\(\begin{array}[t]{rll}
k&=&k_1+k_2+k_3 \\[5pt]
&\approx&130,74\;[\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/53106e65a0b18823f35a29dd43cf1be45830306e2118dcb6d5fa141de36561f2_light.svg)
Im Intervall ![\([50;70]\)](https://www.schullv.de/resources/formulas/36afcfff5c9036023f9b0a4be4cd34b9df9ad8375c762443a07c601503e37d56_light.svg) wird die Bahn durch
wird die Bahn durch  beschrieben. Ableiten der in der Aufgabenstellung gegebenen Funktionsgleichung von
beschrieben. Ableiten der in der Aufgabenstellung gegebenen Funktionsgleichung von  im CAS und Einsetzen in die Formel für die Länge liefert mit Hilfe des CAS:
im CAS und Einsetzen in die Formel für die Länge liefert mit Hilfe des CAS:
![\(\begin{array}[t]{rll}
k_2&=&\displaystyle\int_{50}^{70}\sqrt{1+(g_2](https://www.schullv.de/resources/formulas/32406e0bc1603c0a01c750a51a8f13e39419bc3f1ef8869ad457d00aac3aca4d_light.svg)

e)
Gleichung für  ermitteln
Wegen der Werte aus der Tabelle kommt eine konstante oder lineare Funktion
ermitteln
Wegen der Werte aus der Tabelle kommt eine konstante oder lineare Funktion  nicht infrage. Eintragen der Werte aus der Tabelle im CAS und Durchführen einer quadratischen Regression liefert einen Funktionsgraphen, der zweitweise unterhalb der
nicht infrage. Eintragen der Werte aus der Tabelle im CAS und Durchführen einer quadratischen Regression liefert einen Funktionsgraphen, der zweitweise unterhalb der  -Achse verläuft. Im Sachzusammenhang ist das nicht sinvoll, da das bedeuten würde, dass die Achterbahn dort rückwärts fährt.
-Achse verläuft. Im Sachzusammenhang ist das nicht sinvoll, da das bedeuten würde, dass die Achterbahn dort rückwärts fährt.
Kubische Regression liefert einen Funktionsgraphen für der im betrachteten Zeitraum überhalb der
der im betrachteten Zeitraum überhalb der  -Achse liegt. Für die Funktionsgleichung gilt:
-Achse liegt. Für die Funktionsgleichung gilt:

 Der im CAS angezeigte Korrelationskoeffizient beträgt nahezu
Der im CAS angezeigte Korrelationskoeffizient beträgt nahezu  sodass die erhaltene Funktionsgleichung sehr gut zu den in der Tabelle angegebenen Werten passt und als gute Näherung des Sachverhalts angenommen werden kann.
Flächeninhalt bestimmen
Mit Hilfe des CAS und der eben bestimmten Funktionsgleichung für
sodass die erhaltene Funktionsgleichung sehr gut zu den in der Tabelle angegebenen Werten passt und als gute Näherung des Sachverhalts angenommen werden kann.
Flächeninhalt bestimmen
Mit Hilfe des CAS und der eben bestimmten Funktionsgleichung für  folgt für den gesuchten Flächeninhalt:
folgt für den gesuchten Flächeninhalt:
![\(\begin{array}[t]{rll}
A&=&\displaystyle\int_{0}^{10}v(t)\;\mathrm dt \\[5pt]
&=&50\;[FE]
\end{array}\)](https://www.schullv.de/resources/formulas/c25724508476ac68b3a0cd324129a3c857d470d66151f2f4dfad2dfa9c3878ba_light.svg)
 Ergebnis im Sachzusammenhang interpretieren
Die Funktion
Ergebnis im Sachzusammenhang interpretieren
Die Funktion  beschreibt im Intervall
beschreibt im Intervall  die Geschwindigkeit des Wagens der Achterbahn beim Bremsvorgang. Der über das Integral berechnete Flächeninhalt der betrachteten Fläche unter dem Graphen von
die Geschwindigkeit des Wagens der Achterbahn beim Bremsvorgang. Der über das Integral berechnete Flächeninhalt der betrachteten Fläche unter dem Graphen von  gibt somit den Bremsweg des Wagens in Metern an.
gibt somit den Bremsweg des Wagens in Metern an.
Kubische Regression liefert einen Funktionsgraphen für

a)
Graphen von  und
und  darstellen
Der CAS liefert folgende graphische Darstellung der beiden Funktionen
darstellen
Der CAS liefert folgende graphische Darstellung der beiden Funktionen  und
und  sowie eine Wertetabelle für die beiden betrachteten Funktionen:
sowie eine Wertetabelle für die beiden betrachteten Funktionen:
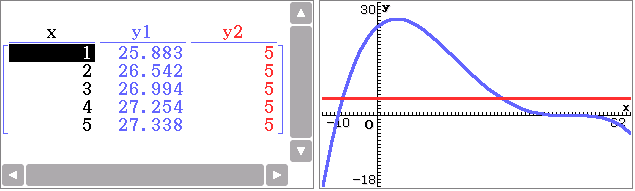 Unter Zuhilfenahme der Wertetabelle und Beachtung der in der Aufgabenstellung angegebenen Intervalle ergibt sich folgende Abbildung:
Unter Zuhilfenahme der Wertetabelle und Beachtung der in der Aufgabenstellung angegebenen Intervalle ergibt sich folgende Abbildung:
 Möglichen Verlauf des Graphen von
Möglichen Verlauf des Graphen von  skizzieren
Der Graph der Funktion
skizzieren
Der Graph der Funktion  soll knickfrei in die beiden bereits eingezeichneten Graphen übergehen, somit ergibt sich ein möglicher Verlauf des Graphen von
soll knickfrei in die beiden bereits eingezeichneten Graphen übergehen, somit ergibt sich ein möglicher Verlauf des Graphen von  wie folgt:
wie folgt:
 Maximale Höhe berechnen
Mit dem CAS folgt für die ersten beiden Ableitungen von
Maximale Höhe berechnen
Mit dem CAS folgt für die ersten beiden Ableitungen von 

 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&=&5 \\[5pt]
x_2&=&50
\end{array}\)](https://www.schullv.de/resources/formulas/cadb9159ed6e503885b973d085ac8696d7e08d5ff5f00a91ba55f4493e479523_light.svg)
 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
g_1](https://www.schullv.de/resources/formulas/5fe4f211c0ce489521f859d54274a47f19b1d59a9704ba437f0665480ae00fe2_light.svg)
 Dem Verlauf des Graphen von
Dem Verlauf des Graphen von  ist zu entnehmen, dass keine Randmaxima existieren. Somit besitzt der Graph von
ist zu entnehmen, dass keine Randmaxima existieren. Somit besitzt der Graph von  an der Stelle
an der Stelle  ein Hochpunkt. Einsetzen von
ein Hochpunkt. Einsetzen von  in
in  liefert die gesuchte maximale Höhe von
liefert die gesuchte maximale Höhe von ![\(g_1(5)\approx27,34\;[\text{m}].\)](https://www.schullv.de/resources/formulas/dcebbf46152157812bffebd9a3310a6f0cddc2360c74c40667929f290ea1fc57_light.svg) Punkt bestimmen, in dem Gefälle am größten ist
Mit dem CAS folgt für die dritte Ableitung von
Punkt bestimmen, in dem Gefälle am größten ist
Mit dem CAS folgt für die dritte Ableitung von 
 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_3&=&20 \\[5pt]
x_4&=&50
\end{array}\)](https://www.schullv.de/resources/formulas/e7ccdae4802d3c7e8a53c749de84ecaf46fcb2e942d6b4fd1ea4ffe9249b27e2_light.svg)
 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
g_1](https://www.schullv.de/resources/formulas/971e9839200799df099c854efaa4bf7034e11ef4a3a2eea309a6588f1fc7497c_light.svg)
 Dem Verlauf des Graphen von
Dem Verlauf des Graphen von  ist zu entnehmen, dass das Gefälle an der Stelle
ist zu entnehmen, dass das Gefälle an der Stelle  größer als an der Stelle
größer als an der Stelle  ist. Einsetzen von
ist. Einsetzen von  in
in  liefert
liefert  Die Koordinaten des Punktes
Die Koordinaten des Punktes  in dem das Gefälle in diesem Intervall am größten ist betragen somit
in dem das Gefälle in diesem Intervall am größten ist betragen somit 







b)
Größe des Winkels bestimmen
Mit dem CAS folgt für die Funktionsgleichung der Normalen im Punkt 
 Da die Normale eine Gerade ist, folgt aus der Funktionsgleichung direkt ihre Steigung von
Da die Normale eine Gerade ist, folgt aus der Funktionsgleichung direkt ihre Steigung von 
 Für den Winkel, den die Normale mit der
Für den Winkel, den die Normale mit der  -Achse einschließt, folgt somit mit dem CAS:
-Achse einschließt, folgt somit mit dem CAS:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&\dfrac{25}{27} \\[5pt]
\alpha&\approx&42,8^\circ
\end{array}\)](https://www.schullv.de/resources/formulas/1b5fbc962eecda577011761a4e7662710a942178a437b6911ae56d06a4906f0a_light.svg) Koordinaten der Punkte bestimmen
Wenn die Sonnenstrahlen einen Winkel von
Koordinaten der Punkte bestimmen
Wenn die Sonnenstrahlen einen Winkel von  mit der Horizontalen einschließen, dann gilt für die Steigung
mit der Horizontalen einschließen, dann gilt für die Steigung  der Normalen an den Graphen
der Normalen an den Graphen  in diesem Punkt:
in diesem Punkt:
 Die Steigung der zugehörigen Tangente an
Die Steigung der zugehörigen Tangente an  und somit der Wert von
und somit der Wert von  an diesem Punkt beträgt damit
an diesem Punkt beträgt damit  Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&\approx&15,51 \\[5pt]
x_2&=&25 \\[5pt]
x_3&\approx&64,5
\end{array}\)](https://www.schullv.de/resources/formulas/c7c466c16b23749646cf2a9cd4bac736dca9c55ff4dae9ce0ac00b830385e739_light.svg) Da
Da ![\(x_3\notin[0;50]\)](https://www.schullv.de/resources/formulas/f636c3c008fa0e1d1cd359b5817e5580dc451ff67d05081676d71db6d8fd5e1b_light.svg) gilt, kommt dieser Wert nicht infrage.
gilt, kommt dieser Wert nicht infrage.
 Einsetzen von
Einsetzen von  und
und  in
in  liefert die Koordinaten
liefert die Koordinaten  und
und  der gesuchten Punkte.
der gesuchten Punkte.


c)
Damit der Graph von  knickfrei in die anderen beiden Graphen übergeht, müssen folgende Bedingungen gelten:
knickfrei in die anderen beiden Graphen übergeht, müssen folgende Bedingungen gelten:
![\(\begin{array}[t]{rll}
g_2(50)&=&g_1(50) \\[5pt]
g_2(70)&=&g_3(70) \\[5pt]
g_2](https://www.schullv.de/resources/formulas/6b0895d22650776b70a84b09e1eaadde1d195f174dc420e772c5908858ef8240_light.svg) Anhand des in Teilaufgabe a) skizzierten Graphen ist ersichtlich, dass
Anhand des in Teilaufgabe a) skizzierten Graphen ist ersichtlich, dass  weder eine lineare noch quadratische Funktion sein kann. Ein möglicher Ansatz ist nun, eine kubische Funktion
weder eine lineare noch quadratische Funktion sein kann. Ein möglicher Ansatz ist nun, eine kubische Funktion  zu konstruieren, das heißt
zu konstruieren, das heißt  und
und  sind der folgenden allgemeinen Formen:
sind der folgenden allgemeinen Formen:

 Mit dem CAS ergeben sich die Werte
Mit dem CAS ergeben sich die Werte 

 und
und  für die obigen Bedingungen. Zusammen mit den allgemeinen Funktionsgleichungen ergibt sich folgendes lineares Gleichungssystem:
für die obigen Bedingungen. Zusammen mit den allgemeinen Funktionsgleichungen ergibt sich folgendes lineares Gleichungssystem:
 Ein möglicher Funktionsterm von
Ein möglicher Funktionsterm von  ist somit gegeben durch
ist somit gegeben durch 

Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
a&=&-\dfrac{1}{800} \\[5pt]
b&=&\dfrac{9}{40} \\[5pt]
c&=&-\dfrac{105}{8} \\[5pt]
d&=&250
\end{array}\)](https://www.schullv.de/resources/formulas/e450c858b16a162c4819461d2af9551c79e04ab2be349e7cd3cc8084f4ba1c7f_light.svg)

d)
1. Schritt: Länge im Intervall ![\(\boldsymbol{[50;70]}\)](https://www.schullv.de/resources/formulas/27f88ad0df2ad5219770fd1f3edab56e49685f0317e1427988e82461c1be48fd_light.svg) berechnen
berechnen
 2. Schritt: Länge im Intervall
2. Schritt: Länge im Intervall ![\(\boldsymbol{[70;120]}\)](https://www.schullv.de/resources/formulas/6b78c0107a3dd91888cb09e302989d2547637d8449cc04bd4cf87a89f1047843_light.svg) berechnen
Im Intervall
berechnen
Im Intervall ![\([70;120]\)](https://www.schullv.de/resources/formulas/1638ab42ace7801b366bfb13ef3e0fc0af718a6118e3a3c1670431f3e25d5fa2_light.svg) wird die Bahn durch
wird die Bahn durch  beschrieben. Da
beschrieben. Da  konstant ist, ergibt sich die Länge der Bahn direkt als Differenz der Randstellen:
konstant ist, ergibt sich die Länge der Bahn direkt als Differenz der Randstellen:
![\(k_3=120-70=50\;[\text{m}]\)](https://www.schullv.de/resources/formulas/fb7f41311e71f24cad6561f3adf426ff53c4809678fc4e1586fadd64d7c9ce25_light.svg) 3. Schritt: Länge im Intervall
3. Schritt: Länge im Intervall ![\(\boldsymbol{[0;120]}\)](https://www.schullv.de/resources/formulas/164c9f69f1a0d652fe950b8e427cd3ac3e0ef38b6d80da86f7608767541b482c_light.svg) berechnen
Für die gesuchte Länge der Bahn folgt nun mit den berechneten Werten:
berechnen
Für die gesuchte Länge der Bahn folgt nun mit den berechneten Werten:
![\(\begin{array}[t]{rll}
k&=&k_1+k_2+k_3 \\[5pt]
&\approx&130,74\;[\text{m}]
\end{array}\)](https://www.schullv.de/resources/formulas/53106e65a0b18823f35a29dd43cf1be45830306e2118dcb6d5fa141de36561f2_light.svg)
Im Intervall ![\([50;70]\)](https://www.schullv.de/resources/formulas/36afcfff5c9036023f9b0a4be4cd34b9df9ad8375c762443a07c601503e37d56_light.svg) wird die Bahn durch
wird die Bahn durch  beschrieben. Ableiten der in der Aufgabenstellung gegebenen Funktionsgleichung von
beschrieben. Ableiten der in der Aufgabenstellung gegebenen Funktionsgleichung von  im CAS und Einsetzen in die Formel für die Länge liefert mit Hilfe des CAS:
im CAS und Einsetzen in die Formel für die Länge liefert mit Hilfe des CAS:
![\(\begin{array}[t]{rll}
k_2&=&\displaystyle\int_{50}^{70}\sqrt{1+(g_2](https://www.schullv.de/resources/formulas/32406e0bc1603c0a01c750a51a8f13e39419bc3f1ef8869ad457d00aac3aca4d_light.svg)

e)
Gleichung für  ermitteln
Wegen der Werte aus der Tabelle kommt eine konstante oder lineare Funktion
ermitteln
Wegen der Werte aus der Tabelle kommt eine konstante oder lineare Funktion  nicht infrage. Eintragen der Werte aus der Tabelle im CAS und Durchführen einer quadratischen Regression liefert einen Funktionsgraphen, der zweitweise unterhalb der
nicht infrage. Eintragen der Werte aus der Tabelle im CAS und Durchführen einer quadratischen Regression liefert einen Funktionsgraphen, der zweitweise unterhalb der  -Achse verläuft. Im Sachzusammenhang ist das nicht sinvoll, da das bedeuten würde, dass die Achterbahn dort rückwärts fährt.
-Achse verläuft. Im Sachzusammenhang ist das nicht sinvoll, da das bedeuten würde, dass die Achterbahn dort rückwärts fährt.
Kubische Regression liefert einen Funktionsgraphen für der im betrachteten Zeitraum überhalb der
der im betrachteten Zeitraum überhalb der  -Achse liegt. Für die Funktionsgleichung gilt:
-Achse liegt. Für die Funktionsgleichung gilt:

 Der im CAS angezeigte Korrelationskoeffizient beträgt nahezu
Der im CAS angezeigte Korrelationskoeffizient beträgt nahezu  sodass die erhaltene Funktionsgleichung sehr gut zu den in der Tabelle angegebenen Werten passt und als gute Näherung des Sachverhalts angenommen werden kann.
Flächeninhalt bestimmen
Mit Hilfe des CAS und der eben bestimmten Funktionsgleichung für
sodass die erhaltene Funktionsgleichung sehr gut zu den in der Tabelle angegebenen Werten passt und als gute Näherung des Sachverhalts angenommen werden kann.
Flächeninhalt bestimmen
Mit Hilfe des CAS und der eben bestimmten Funktionsgleichung für  folgt für den gesuchten Flächeninhalt:
folgt für den gesuchten Flächeninhalt:
![\(\begin{array}[t]{rll}
A&=&\displaystyle\int_{0}^{10}v(t)\;\mathrm dt \\[5pt]
&=&50\;[FE]
\end{array}\)](https://www.schullv.de/resources/formulas/c25724508476ac68b3a0cd324129a3c857d470d66151f2f4dfad2dfa9c3878ba_light.svg) Ergebnis im Sachzusammenhang interpretieren
Die Funktion
Ergebnis im Sachzusammenhang interpretieren
Die Funktion  beschreibt im Intervall
beschreibt im Intervall  die Geschwindigkeit des Wagens der Achterbahn beim Bremsvorgang. Der über das Integral berechnete Flächeninhalt der betrachteten Fläche unter dem Graphen von
die Geschwindigkeit des Wagens der Achterbahn beim Bremsvorgang. Der über das Integral berechnete Flächeninhalt der betrachteten Fläche unter dem Graphen von  gibt somit den Bremsweg des Wagens in Metern an.
gibt somit den Bremsweg des Wagens in Metern an.
Kubische Regression liefert einen Funktionsgraphen für