Stochastik
Aufgabe 2A
Bei einer Naturkostkette besitzen die meisten Kundinnen und Kunden ein Konto für Online-Bestellungen. Im Folgenden werden ausschließlich diese Personen betrachtet. der Personen sind jünger als
Jahre.
der Personen sind jünger als
Jahre und wohnen nicht in einer Großstadt. Der Anteil der Personen, die in einer Großstadt wohnen, beträgt
Es soll davon ausgegangen werden, dass in einer zufälligen Auswahl von Personen die Anzahl derjenigen, die in einer Großstadt wohnen, binomialverteilt ist.
Stelle den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.
Beurteile die folgende Aussage:
Die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person entweder in einer Großstadt wohnt oder nicht jünger als Jahre ist, ist kleiner als
Beschreibe im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses wie folgt berechnet werden kann:
Gib den Wert des Terms an und gib die Bedeutung des Terms im Sachzusammenhang an.
Die Naturkostkette produziert Gläser mit veganem Brotaufstrich. Diese Gläser werden in Kisten verpackt; jede Kiste enthält Gläser. Für die Naturkostkette belaufen sich die Gesamtkosten auf
pro Glas.
Ein Glas weist mit einer Wahrscheinlichkeit von einen optischen Mangel auf. Die Naturkostkette legt daher generell für die Bezahlung einer gelieferten Kiste Folgendes fest:
- Wenn höchstens sechs Gläser diesen Mangel aufweisen, so muss für die Kiste der vollständige Preis bezahlt werden.
- Wenn genau sieben oder genau acht Gläser diesen Mangel aufweisen, so muss für die Kiste der halbe Preis bezahlt werden.
- Wenn mehr als acht Gläser diesen Mangel aufweisen, so muss für die Kiste nichts bezahlt werden.
Die in den folgenden Teilaufgaben aufgeführten Näherungswerte für Wahrscheinlichkeiten sollen bei Verwendung in weiteren Rechnungen als exakte Werte betrachtet werden.
Zeige, dass die Wahrscheinlichkeit dafür, dass in einer der Produktion entnommenen Kiste höchstens sechs Gläser den Mangel aufweisen, etwa beträgt.
Die Wahrscheinlichkeit dafür, dass in einer der Produktion entnommenen Kiste genau sieben oder genau acht Gläser diesen Mangel aufweisen, beträgt etwa
Es wird davon ausgegangen, dass bei jeder Lieferung alle Gläser von der Kundin bzw. vom Kunden überprüft werden und die Anzahl der Gläser mit diesem Mangel der Naturkostkette wahrheitsgemäß rückgemeldet wird.
Ermittle den geringsten Preis pro Glas mit veganem Brotaufstrich auf Cent genau, so dass die Naturkostkette im Mittel einen Gewinn von mindestens pro Glas erwarten kann.
Aufgabe 2B
Betrachtet wird ein Brettspiel mit zwei Würfeln, deren Seiten jeweils mit den Zahlen bis
durchnummeriert sind. In jedem Spielzug werden beide Würfel geworfen. Wenn sich dabei die Augensumme
oder
ergibt, wird eine Ereigniskarte aufgedeckt, ansonsten nicht.
Begründe, dass die Wahrscheinlichkeit dafür, dass in einem Spielzug eine Ereigniskarte aufgedeckt wird, beträgt.
Betrachtet werden die ersten fünf Spielzüge.
Beschreibe im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit mit dem Term berechnet werden kann.
Die Zufallsgröße beschreibt die Anzahl der in einem Spiel mit
Spielzügen insgesamt aufgedeckten Ereigniskarten.
Berechne die Wahrscheinlichkeit dafür, dass im Laufe dieses Spiels weniger als zwölf Ereigniskarten aufgedeckt werden.
Die Abbildung 1 zeigt die Wahrscheinlichkeitsverteilung von
Skaliere in der Abbildung die beiden Achsen, indem du jeweils einen geeigneten Wert ermittelst und diesen auf der zugehörigen Achse einträgst.
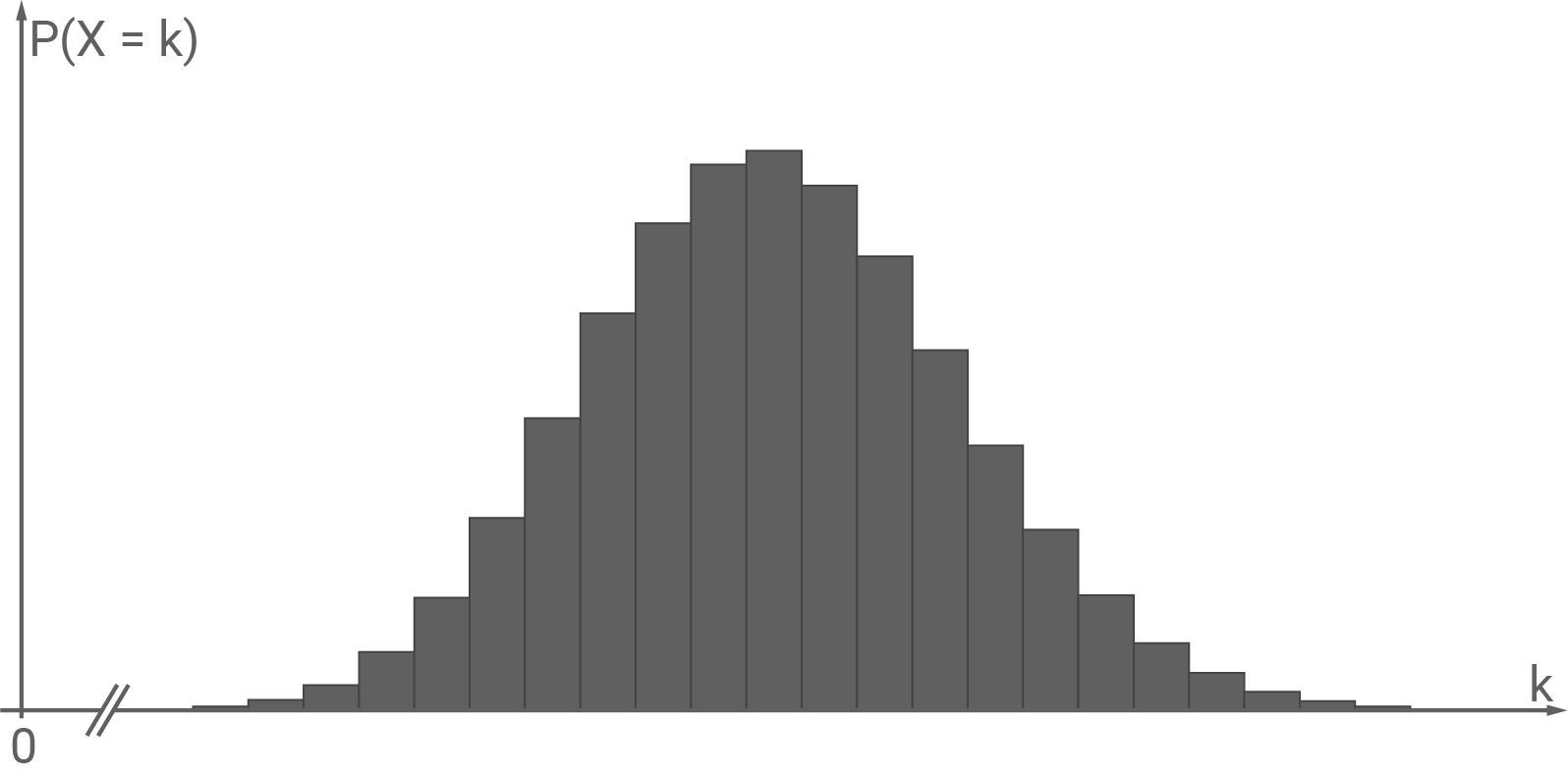
Zu dem Brettspiel gehören Plättchen, auf denen Landschaften und Tiere abgebildet sind. Es kommen genau drei verschiedene Landschaftssymbole und zwei verschiedene Tiersymbole vor. Auf jedem Plättchen sind genau zwei Landschaftssymbole und ein oder zwei Tiersymbole abgebildet, wobei kein Symbol doppelt vorkommt. Zwei Plättchen gelten als gleich, wenn auf ihnen genau die gleichen Symbole abgebildet sind.
Ermittle die Anzahl der verschiedenen Plättchen, die es bei diesem Spiel höchstens geben kann.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Aufgabe 2A
Die Aussage ist falsch, da ist.
In einem Zufallsexperiment werden insgesamt Personen nach dem Zufallsprinzip ausgewählt. Jede dieser Personen hat mit einer Wahrscheinlichkeit von
ihren Wohnsitz in einer Großstadt. Der gegebene Summen-Term beschreibt die Wahrscheinlichkeit dafür, dass unter diesen
ausgewählten Personen mindestens
und höchstens
Personen in einer Großstadt leben.
Durch Ausrechnen mit dem GTR folgt für den Wert des Terms ungefähr Das bedeutet: Die Wahrscheinlichkeit, dass zwischen
und
der
zufällig gewählten Personen in einer Großstadt leben, liegt bei etwa
ist eine binomialverteilte Zufallsgröße mit den Parametern
und
Sie gibt die Anzahl der Gläser in der Kiste, die den Mangel aufweisen, an.
Wahrscheinlichkeit für volle Bezahlung (höchstens 6 mangelhafte Gläser):
Wahrscheinlichkeit für halbe Bezahlung (genau 7 oder 8 mangelhafte Gläser):
Wahrscheinlichkeit für keine Bezahlung (mehr als 8 mangelhafte Gläser):
Mit dem solve-Befehl des GTR folgt:
Der geringstmögliche Preis pro Glas beträgt also Euro.
Aufgabe 2B
Um die Augensumme mit zwei Würfeln zu erzielen gibt es
verschiedene Kombinationen:
Somit beträgt die Wahrscheinlichkeit, die Augensumme zu erzielen
Um die Augensumme mit zwei Würfeln zu erzielen gibt es
verschiedene Kombinationen:
Somit beträgt die Wahrscheinlichkeit, die Augensumme zu erzielen
Addiert ergibt das:
In den ersten fünf Spielzügen werden fünf Ereigniskarten aufgedeckt oder es wird keine Ereigniskarte aufgedeckt.
Geeignete Werte ermitteln
Achsen skalieren
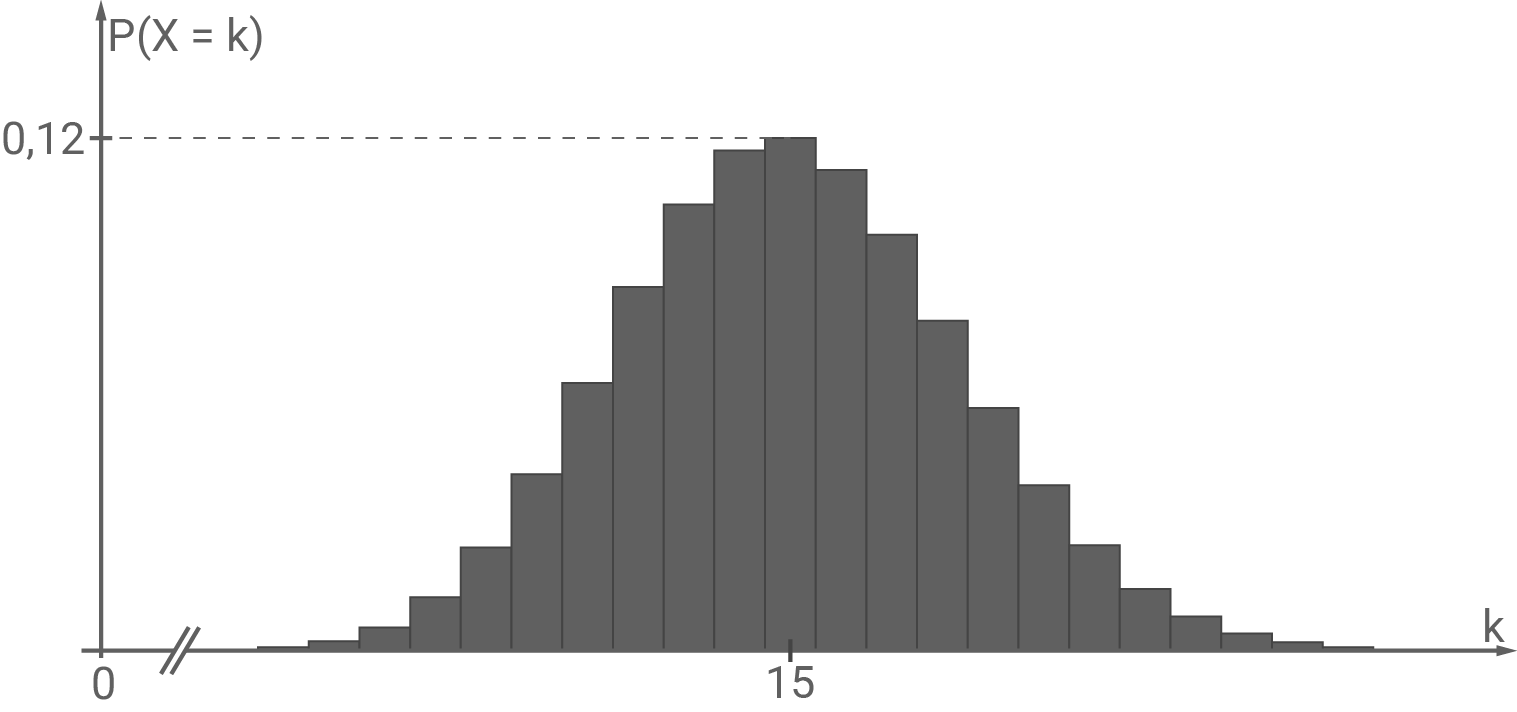
Aus Landschaftssymbolen sollen jeweils
ohne Reihenfolge ausgewählt werden. Das ist eine Kombination ohne Zurücklegen:
Es gibt Tiersymbole. Ein Plättchen kann
oder
verschiedene Tiere enthalten:
- Wählt man
Tier, gibt es
Möglichkeiten
- Wählt man
Tier, gibt es
Möglichkeit
Für jedes Landschaftspaar kann eine der Tierkombinationen gewählt werden:
Es kann bei diesem Spiel höchstens verschiedene Plättchen geben.