Wahlaufgabe 2
Aufgabe R1
Gegeben ist die in definierte Funktion
mit
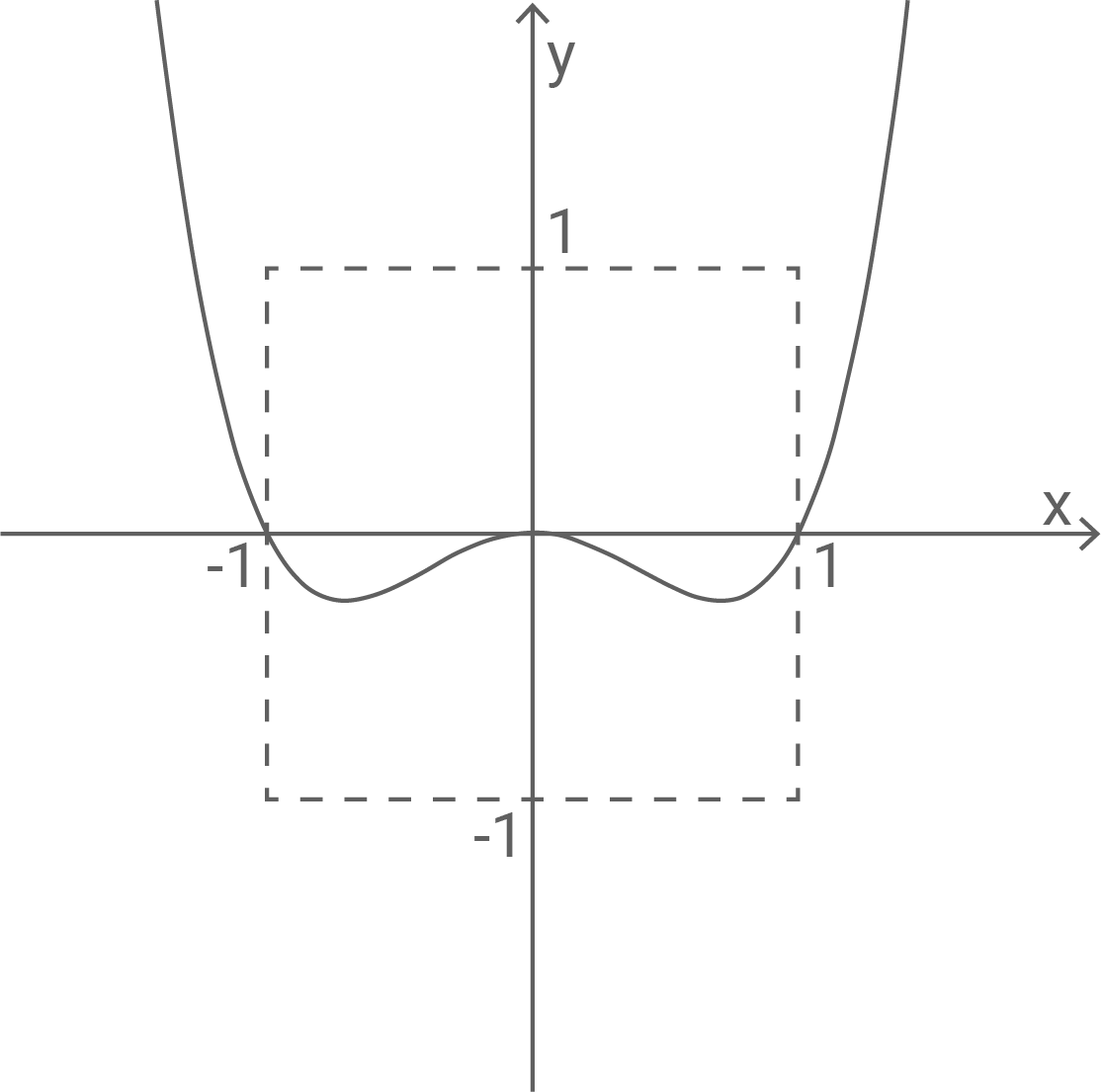
Die Abbildung zeigt ein zu beiden Koordinatenachsen symmetrisches Quadrat mit der Seitenlänge
sowie den Graphen von
Der Graph von wird um
in
-Richtung verschoben.
Skizziere den verschobenen Graphen in der Abbildung.
Der Graph von wird nun um
mit
in
-Richtung verschoben, sodass der Graph das Quadrat in zwei Flächen gleichen Inhalts teilt.
Berechne
Aufgabe R2
Die Abbildung zeigt die Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße mit den Parametern
und
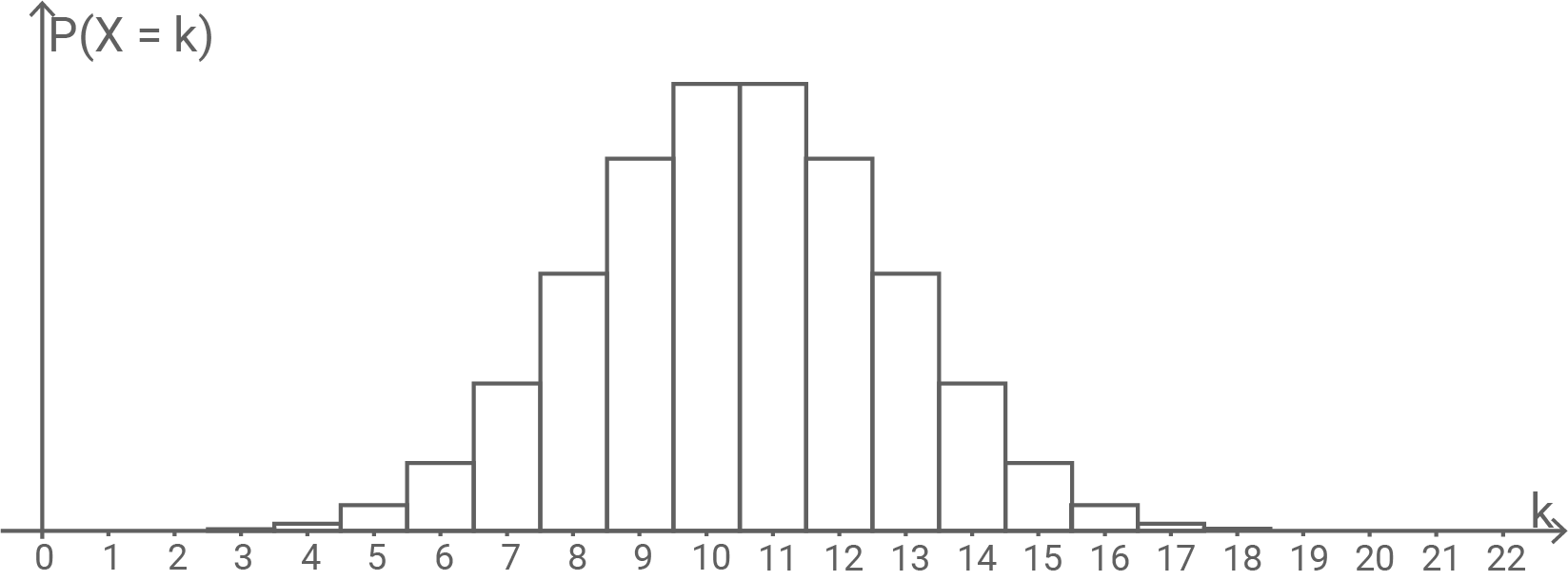
Es gilt
Begründe, dass nicht gerade ist.
Es gilt und
Berechne unter Verwendung dieser Werte näherungsweise die Wahrscheinlichkeit
Aufgabe R3
Die Ebene wird durch die Gleichung
mit
beschrieben.
Zeige, dass der Vektor senkrecht zur Ebene
steht.
Bestimme die Koordinaten eines Punkts mit folgender Eigenschaft:
Wird der Punkt an der Ebene
gespiegelt, so hat der entstehende Punkt vom Punkt
den Abstand
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Aufgabe R1
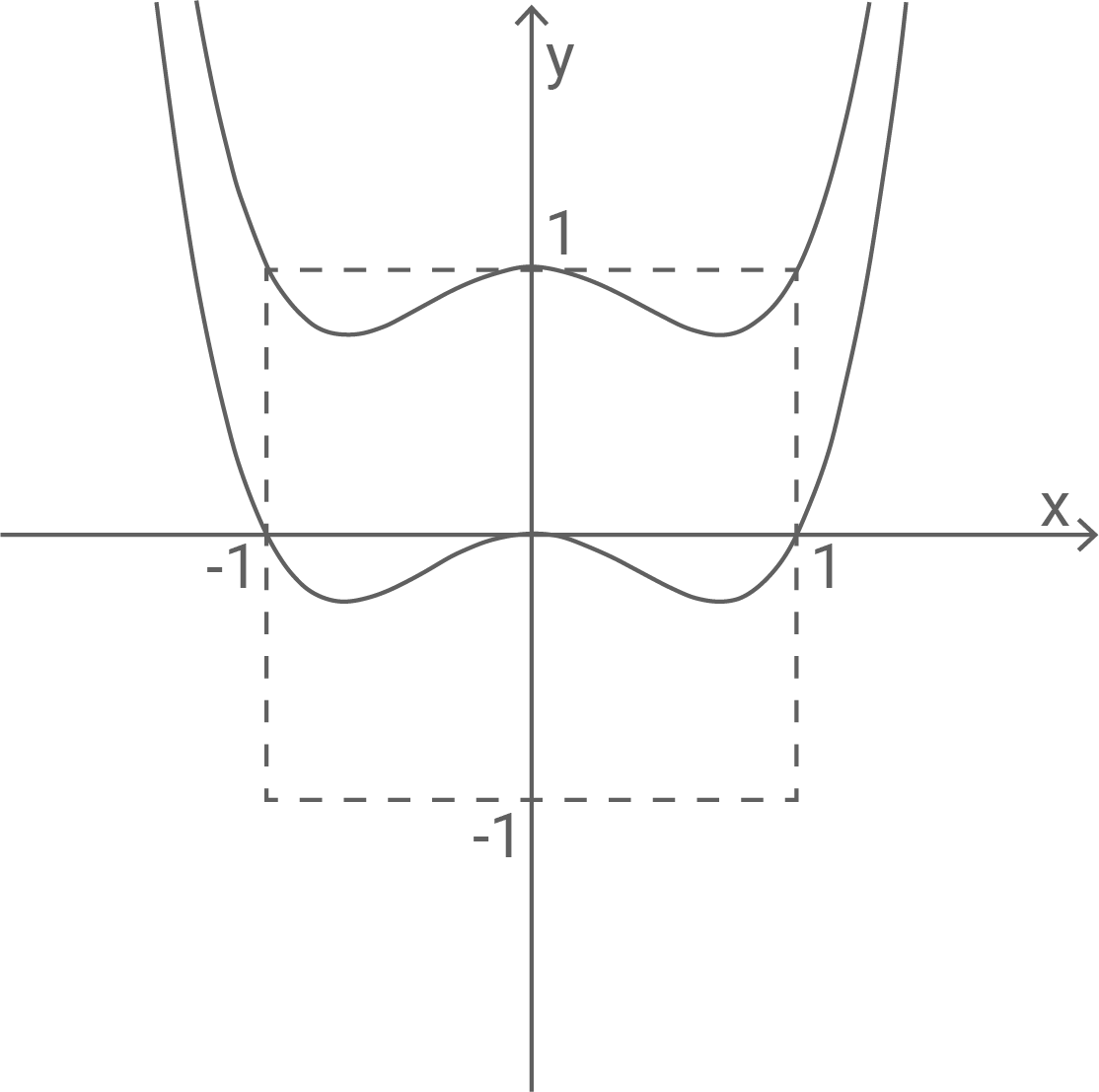
Wegen der Symmetrie genügt es, nur den Bereich von bis
zu betrachten und dort die Fläche über dem Graphen mit der Fläche unterhalb gleichzusetzen.
Damit die Funktion das Quadrat halbiert, muss die Bilanz des Integrals gleich sein:
Aufgabe R2
Da die Wahrscheinlichkeiten bei und
gleich groß und am größten sind, liegt der Erwartungswert
genau dazwischen - also zwischen zwei ganzen Zahlen. Das geht nur, wenn
ungerade ist.
Gegeben ist und
Wegen der Symmetrie gilt dann auch
Außerdem ist also folgt:
Aufgabe R3
Ein Vektor steht genau dann senkrecht zur Ebene
wenn er senkrecht zu beiden Spannvektoren der Ebene ist.
Um das zu überprüfen, wird jeweils das Skalarprodukt berechnet.
Skalarprodukt mit berechnen
Skalarprodukt mit berechnen
Da beide Skalarprodukte null sind, steht der Vektor senkrecht zur Ebene
Gegeben ist der Normalenvektor
Länge des Vektors berechnen
Der Einheitsvektor von ist also
ist der gespiegelte Punkt von
an der Ebene
Insgesamt sollen und
einen Abstand von
haben. Somit müssen die Punkte einen Abstand von
zur Ebene
haben.
Ein möglicher Spiegelpunkt auf der Ebene ist der Stützvektor der Ebene
Koordinaten eines Punktes berechnen