Aufgabe 2B
Beim Vereinsfest eines Angelvereins kann man aus zwei Becken Plastikfische angeln, von denen einige auf der Unterseite mit einem Gewinnpunkt markiert sind.
a) Im ersten Becken befinden sich 15 Fische, von denen fünf mit einem Gewinnpunkt markiert sind. Es werden zufällig drei Fische ohne Zurücklegen geangelt.
Bestimmen Sie die Wahrscheinlichkeiten der folgenden Ereignisse: :
:  Es werden genau zwei Gewinnpunkte erzielt.
Es werden genau zwei Gewinnpunkte erzielt.
 :
:  Es wird mindestens ein Gewinnpunkt erzielt.
Es wird mindestens ein Gewinnpunkt erzielt.
Bestimmen Sie die Wahrscheinlichkeiten der folgenden Ereignisse:
(6P)
b) Beim zweiten Becken wird jeder geangelte Fisch vor dem nächsten Angeln wieder ins Becken zurückgelegt. Der Term  beschreibt die Wahrscheinlichkeit für einen einfachen Gewinn und der Term
beschreibt die Wahrscheinlichkeit für einen einfachen Gewinn und der Term  die Wahrscheinlichkeit für einen Hauptgewinn.
die Wahrscheinlichkeit für einen Hauptgewinn.
Geben Sie an, welche Aussagen sich aus den obigen Termen
Berechnen Sie die Wahrscheinlichkeit, dass bei diesem Spiel genau drei Gewinnpunkte erzielt werden.
Geben Sie an, welche Aussagen sich aus den obigen Termen
- über den Anteil der Fische mit Gewinnpunkt und
- über die Spielregeln
Berechnen Sie die Wahrscheinlichkeit, dass bei diesem Spiel genau drei Gewinnpunkte erzielt werden.
(6P)
c) Der Präsident des Angelvereins behauptet, dass im großen See mindestens 10.000 Fische leben. Zur Schätzung der tatsächlichen Fischanzahl wurden 283 Fische gefangen, markiert und wieder im See ausgesetzt. Anschließend werden bei einer Zufallsstichprobe 639 Fische gefangen, von denen 25 markiert sind.
Untersuchen Sie mit einem Vertrauensintervall ), ob die Behauptung des Präsidenten auf Basis dieser Stichprobe widerlegt werden kann.
), ob die Behauptung des Präsidenten auf Basis dieser Stichprobe widerlegt werden kann.
Untersuchen Sie mit einem Vertrauensintervall
(5P)
(17P)
a)  Wahrscheinlichkeiten berechnen
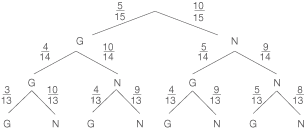
Deine Aufgabe ist es, die Wahrscheinlichkeiten zweier Ereignisse zu berechnen. Hierbei sind 15 Fische in dem betrachteten Becken, von denen 5 Fische einen Gewinnpunkt tragen, und es werden nacheinander drei Fische geangelt. Dabei handelt es sich um ein Ziehen ohne Zurücklegen. Zur Hilfe kannst du ein Baumdiagramm wie das folgende skizzieren. Dabei steht G für einen Gewinn und N für eine Niete.
Wahrscheinlichkeiten berechnen
Deine Aufgabe ist es, die Wahrscheinlichkeiten zweier Ereignisse zu berechnen. Hierbei sind 15 Fische in dem betrachteten Becken, von denen 5 Fische einen Gewinnpunkt tragen, und es werden nacheinander drei Fische geangelt. Dabei handelt es sich um ein Ziehen ohne Zurücklegen. Zur Hilfe kannst du ein Baumdiagramm wie das folgende skizzieren. Dabei steht G für einen Gewinn und N für eine Niete.
 Du kannst die gesuchten Wahrscheinlichkeiten mit Hilfe der Pfadregeln berechnen.
Du kannst die gesuchten Wahrscheinlichkeiten mit Hilfe der Pfadregeln berechnen.
Definiere dazu zunächst eine Zufallsvariable . Díe Zufallsvariable
. Díe Zufallsvariable  beschreibt die Anzahl der Gewinne.
Ereignis
beschreibt die Anzahl der Gewinne.
Ereignis  Hierbei handelt es sich um das Ereignis, dass genau zwei Gewinnfische geangelt werden. Mit Hilfe der Pfadregeln und dem Baumdiagramm ergibt sich hier:
Hierbei handelt es sich um das Ereignis, dass genau zwei Gewinnfische geangelt werden. Mit Hilfe der Pfadregeln und dem Baumdiagramm ergibt sich hier:
 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  werden genau zwei Gewinnpunkte erzielt.
Ereignis
werden genau zwei Gewinnpunkte erzielt.
Ereignis  Hierbei handelt es sich um das Ereignis, dass mindestens ein Gewinnfisch geangelt wird. Du suchst also die Wahrscheinlichkeit
Hierbei handelt es sich um das Ereignis, dass mindestens ein Gewinnfisch geangelt wird. Du suchst also die Wahrscheinlichkeit  .
.
Diese kannst du wieder mit Hilfe der Pfadregeln und des obigen Baumdiagramms berechnen. Du kannst hierbei auch den Trick des Gegenereignisses anwenden, damit du weniger Pfade addieren musst: Dann ergibt sich:
Dann ergibt sich:
 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  wird mindestens ein Gewinnpunkt erzielt.
wird mindestens ein Gewinnpunkt erzielt.

Definiere dazu zunächst eine Zufallsvariable
Diese kannst du wieder mit Hilfe der Pfadregeln und des obigen Baumdiagramms berechnen. Du kannst hierbei auch den Trick des Gegenereignisses anwenden, damit du weniger Pfade addieren musst:
b)  Aussagen ableiten
In diesem Aufgabenteil sollst du dich mit dem zweiten Becken beschäftigen. In diesem Becken wird jeder Fisch vor dem nächsten Angelversuch zurück ins Becken gelegt. Hierbei handelt es sich also um ein Ziehen mit Zurücklegen.
Aussagen ableiten
In diesem Aufgabenteil sollst du dich mit dem zweiten Becken beschäftigen. In diesem Becken wird jeder Fisch vor dem nächsten Angelversuch zurück ins Becken gelegt. Hierbei handelt es sich also um ein Ziehen mit Zurücklegen.
Du weißt hier nicht, wie viele Fische im Becken sind, und auch nicht wie hoch der Anteil der Gewinnfische ist. Dir ist der folgende Term gegeben, der die Wahrscheinlichkeit für einen einfachen Gewinn beschreibt:
 Zusätzlich ist dir noch ein zweiter Term gegeben, der die Wahrscheinlichkeit für einen Hauptgewinn darstellt:
Zusätzlich ist dir noch ein zweiter Term gegeben, der die Wahrscheinlichkeit für einen Hauptgewinn darstellt:
 Aus diesen beiden Termen sollst du nun Aussagen über die Spielregeln, sowie über den Anteil der Gewinnfische ableiten.
Du kannst dazu beide Terme getrennt betrachten. Beginne mit dem ersten Term und überlege dir, ob dich dieser Term an eine Formel erinnert, die du bereits kennst.
Mit dieser Erkenntnis kannst du dann den zweiten Term interpretieren.
1. Schritt: Ersten Term betrachten
Aus diesen beiden Termen sollst du nun Aussagen über die Spielregeln, sowie über den Anteil der Gewinnfische ableiten.
Du kannst dazu beide Terme getrennt betrachten. Beginne mit dem ersten Term und überlege dir, ob dich dieser Term an eine Formel erinnert, die du bereits kennst.
Mit dieser Erkenntnis kannst du dann den zweiten Term interpretieren.
1. Schritt: Ersten Term betrachten
 Dieser Term hat Ähnlichkeit mit der Formel für die Binomialverteilung. Ist
Dieser Term hat Ähnlichkeit mit der Formel für die Binomialverteilung. Ist  eine binomialverteilte Zufallsvariable mit den Parametern
eine binomialverteilte Zufallsvariable mit den Parametern  und
und  , so gilt:
, so gilt:
 Vergleichst du nun, den obigen Term mit dieser Formel, so kannst du davon ausgehen, dass der Term eine Wahrscheinlichkeit der Form
Vergleichst du nun, den obigen Term mit dieser Formel, so kannst du davon ausgehen, dass der Term eine Wahrscheinlichkeit der Form  für eine binomialverteilte Zufallsvariable
für eine binomialverteilte Zufallsvariable  beschreibt. Die Parameter kannst du dabei ablesen, sodass du erhältst:
beschreibt. Die Parameter kannst du dabei ablesen, sodass du erhältst:
 ,
,  und
und  Da es sich im gegebenen Sachverhalt um ein Ziehen mit Zurücklegen handelt und nur zwei Merkmalsausprägungen unterschieden werden, kannst du nun diese Erkenntnisse auf den Sachzusammenhang übertragen.
Nimmst du
Da es sich im gegebenen Sachverhalt um ein Ziehen mit Zurücklegen handelt und nur zwei Merkmalsausprägungen unterschieden werden, kannst du nun diese Erkenntnisse auf den Sachzusammenhang übertragen.
Nimmst du  als Wahrscheinlichkeit dafür, einen Gewinnfisch zu angeln , und
als Wahrscheinlichkeit dafür, einen Gewinnfisch zu angeln , und  als Anzahl der Angelversuche an, so kannst du den obigen Term als Wahrscheinlichkeit dafür in fünf Versuchen vier Gewinnpunkte zu erzielen interpretieren.
als Anzahl der Angelversuche an, so kannst du den obigen Term als Wahrscheinlichkeit dafür in fünf Versuchen vier Gewinnpunkte zu erzielen interpretieren.
Daran kannst du auch erkennen, dass ein einfacher Gewinn darin besteht, in fünf Versuchen vier Gewinnpunkte zu erzielen. 2. Schritt: Zweiten Term betrachten Der zweite Term ist dir gegeben mit:
 Dieser Term beschreibt die Wahrscheinlichkeit dafür, einen Hauptgewinn zu erzielen. Du weißt bereits, dass in diesem Spiel fünfmal geangelt wird und der Anteil der Gewinnfische
Dieser Term beschreibt die Wahrscheinlichkeit dafür, einen Hauptgewinn zu erzielen. Du weißt bereits, dass in diesem Spiel fünfmal geangelt wird und der Anteil der Gewinnfische  beträgt. Daraus kannst du ableiten, dass der hier betrachtete Term die Wahrscheinlichkeit beschreibt, dass in fünf Versuchen genau fünf Gewinnfische geangelt werden.
beträgt. Daraus kannst du ableiten, dass der hier betrachtete Term die Wahrscheinlichkeit beschreibt, dass in fünf Versuchen genau fünf Gewinnfische geangelt werden.
Der Hauptgewinn besteht also darin in fünf Versuchen fünf Fische mit einem Gewinnpunkt zu angeln. Insgesamt lässt sich aus den beiden Termen also folgendes ableiten: Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, genau drei Gewinnpunkte zu erzielen. Oben hast du die Formel für die Binomialverteilung bereits gesehen und weißt, dass solche Wahrscheinlichkeiten mit dieser berechnet werden können. Betrachtest du hier die Zufallsvariable
Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, genau drei Gewinnpunkte zu erzielen. Oben hast du die Formel für die Binomialverteilung bereits gesehen und weißt, dass solche Wahrscheinlichkeiten mit dieser berechnet werden können. Betrachtest du hier die Zufallsvariable  , die die zufällige Anzahl der Fische mit Gewinnpunkten beschreibt, so ist
, die die zufällige Anzahl der Fische mit Gewinnpunkten beschreibt, so ist  binomialverteilt mit den Parametern
binomialverteilt mit den Parametern  und
und  . Du suchst hier also
. Du suchst hier also  .
.
Diese kannst du handschriftlich mit der obigen Formel für die Binomialverteilung berechnen, oder auch mit dem CAS. Lösungsweg A: Formel für die Binomialverteilung
Lösungsweg A: Formel für die Binomialverteilung

 Lösungsweg B: CAS
Hierbei kannst du den binompdf-Befehl des CAS verwenden. Diesen findest du unter:
Lösungsweg B: CAS
Hierbei kannst du den binompdf-Befehl des CAS verwenden. Diesen findest du unter:
 ,
,  und
und  ein, so erhältst du das folgende Ergebnis:
ein, so erhältst du das folgende Ergebnis:

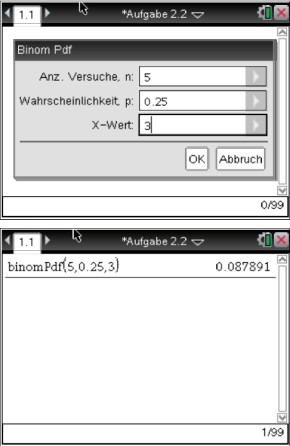 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  werden in diesem Spiel genau drei Gewinnpunkte erzielt.
werden in diesem Spiel genau drei Gewinnpunkte erzielt.
Du weißt hier nicht, wie viele Fische im Becken sind, und auch nicht wie hoch der Anteil der Gewinnfische ist. Dir ist der folgende Term gegeben, der die Wahrscheinlichkeit für einen einfachen Gewinn beschreibt:
Daran kannst du auch erkennen, dass ein einfacher Gewinn darin besteht, in fünf Versuchen vier Gewinnpunkte zu erzielen. 2. Schritt: Zweiten Term betrachten Der zweite Term ist dir gegeben mit:
Der Hauptgewinn besteht also darin in fünf Versuchen fünf Fische mit einem Gewinnpunkt zu angeln. Insgesamt lässt sich aus den beiden Termen also folgendes ableiten:
- Der Anteil der Fische mit Gewinnpunkt liegt bei
.
- Es wird fünfmal geangelt.
- Werden vier Gewinnpunkte erzielt, so gibt es einen einfachen Gewinn.
- Werden fünf Gewinnpunkte erzielt, so gibt es einen Hauptgewinn.
Diese kannst du handschriftlich mit der obigen Formel für die Binomialverteilung berechnen, oder auch mit dem CAS.
menu  5: Wahrscheinlichkeit
5: Wahrscheinlichkeit  5: Verteilungen
5: Verteilungen  D: Binomial Pdf
D: Binomial Pdf
Gibst du dort die entsprechenden Parameter 
c)  Behauptung des Präsidenten mit Hilfe eines Vertrauensintervalls untersuchen
In diesem Aufgabenteil geht es nun um einen See. Der Präsident des Angelvereins behauptet, dass in diesem See mindestens
Behauptung des Präsidenten mit Hilfe eines Vertrauensintervalls untersuchen
In diesem Aufgabenteil geht es nun um einen See. Der Präsident des Angelvereins behauptet, dass in diesem See mindestens  Fische leben. Um die tatsächliche Anzahl der Fische zu schätzen wurden
Fische leben. Um die tatsächliche Anzahl der Fische zu schätzen wurden  Fische gefangen, markiert und wieder zurückgelegt.
Fische gefangen, markiert und wieder zurückgelegt.
Nun wird eine Stichprobe von Fischen entnommen. Davon sind
Fischen entnommen. Davon sind  Fische markiert. Anhand dieser Stichprobe sollst du nun ein Vertrauensintervall mit einer Vertrauenswahrscheinlichkeit von
Fische markiert. Anhand dieser Stichprobe sollst du nun ein Vertrauensintervall mit einer Vertrauenswahrscheinlichkeit von  aufstellen, und so überprüfen, ob die Behauptung des Präsidenten widerlegt werden kann.
Wenn der Präsident Recht hat, dann darf der Anteil
aufstellen, und so überprüfen, ob die Behauptung des Präsidenten widerlegt werden kann.
Wenn der Präsident Recht hat, dann darf der Anteil  der markierten Fische höchstens
der markierten Fische höchstens  betragen. Gesucht ist nun also ein Vertrauensintervall über den Anteil der markierten Fische im See. Liegt
betragen. Gesucht ist nun also ein Vertrauensintervall über den Anteil der markierten Fische im See. Liegt  innerhalb dieses Intervalls, so kann nicht ausgeschlossen werden, dass der Präsident Recht hat, andernfalls, kann davon ausgegangen werden, dass der Präsident mit seiner Behauptung falsch liegt.
Das Vertrauensintervall wird dabei ausgehend von der Stichprobe mit
innerhalb dieses Intervalls, so kann nicht ausgeschlossen werden, dass der Präsident Recht hat, andernfalls, kann davon ausgegangen werden, dass der Präsident mit seiner Behauptung falsch liegt.
Das Vertrauensintervall wird dabei ausgehend von der Stichprobe mit  Fischen, von denen
Fischen, von denen  markiert sind, bestimmt.
Das Vertrauensintervall soll sich auf den Anteil
markiert sind, bestimmt.
Das Vertrauensintervall soll sich auf den Anteil  der Fische im See beziehen, der in diesem Fall unbekannt ist. Einen ersten Schätzwert für
der Fische im See beziehen, der in diesem Fall unbekannt ist. Einen ersten Schätzwert für  kannst du über die Angabe ermitteln, dass von
kannst du über die Angabe ermitteln, dass von  Fischen
Fischen  markiert sind:
markiert sind:
 .
Gesucht ist nun ein Intervall, in dem der tatsächliche Anteil
.
Gesucht ist nun ein Intervall, in dem der tatsächliche Anteil  der markierten Fische mit einer Wahrscheinlichkeit von 95 % liegt. Einen Ansatz für dieses Problem bieten die
der markierten Fische mit einer Wahrscheinlichkeit von 95 % liegt. Einen Ansatz für dieses Problem bieten die  -Regeln.
Du kannst also so vorgehen:
-Regeln.
Du kannst also so vorgehen:
 -Regel auswählen
Du findest die Regel
-Regel auswählen
Du findest die Regel
 2. Schritt: Ausdruck umformen
Betrachte nur den Ausdruck in Klammern und forme ihn so um, dass er eine Aussage über
2. Schritt: Ausdruck umformen
Betrachte nur den Ausdruck in Klammern und forme ihn so um, dass er eine Aussage über  macht. Du kennst bereits:
macht. Du kennst bereits:
![\( \begin{array}{rrrl}
\mu-1,96\sigma &\leq & X &\leq& \mu+1,96\sigma&\scriptsize \mid\; \mu=n\cdot p\\[5pt]
n\cdot p-1,96\sigma &\leq & X &\leq& n\cdot p+1,96\sigma&\scriptsize \mid\; \sigma=\sqrt{n\cdot p\cdot (1-p)}\\[5pt]
n\cdot p-1,96\cdot\sqrt{n\cdot p\cdot (1-p)} &\leq& X &\leq& n\cdot p+1,96\sqrt{n\cdot p\cdot (1-p)}&\scriptsize \mid\; :n\\[5pt]
p-1,96\cdot\sqrt{\frac{p\cdot (1-p)}{n}} &\leq& \frac{X}{n} &\leq& p+1,96\sqrt{\frac{p\cdot (1-p)}{n}}&\scriptsize \mid\; -p\\[5pt]
-1,96\cdot\sqrt{\frac{p\cdot (1-p)}{n}} &\leq& \frac{X}{n}-p &\leq& 1,96\sqrt{\frac{p\cdot (1-p)}{n}}\\[5pt]
\left|\frac{X}{n}-p\right| &\leq& 1,96\sqrt{\frac{p\cdot (1-p)}{n}}&&&\scriptsize \mid\; \frac{X}{n}=0,0391;\qquad n=639\\[5pt]
\left|0,0391-p\right| &\leq& 1,96\sqrt{\frac{p\cdot (1-p)}{639}}&\scriptsize \\
\end{array}\)](https://www.schullv.de/resources/formulas/572eda1da4a9fb286761b50d6f332031a943d15715826a94935350454e5dbe31_light.svg) 3. Schritt: Ungleichung lösen
Du kannst auf beiden Seiten quadrieren und die Ungleichung nach
3. Schritt: Ungleichung lösen
Du kannst auf beiden Seiten quadrieren und die Ungleichung nach  auflösen.
auflösen.
![\( \begin{array}{rll}
\left|0,0391-p\right| &\leq& 1,96\sqrt{\frac{p\cdot (1-p)}{639}}&\scriptsize \mid\; (\;)^2\\[5pt]
(0,0391-p)^2 &\leq& (1,96)^2\cdot\frac{p\cdot(1-p)}{639}&\scriptsize \\[5pt]
0,0391^2-2\cdot0,0391\cdot p+p^2 &\leq& \frac{3,8416}{639}\cdot p\cdot(1-p)&\scriptsize \\[5pt]
0,0391^2-2\cdot0,0391\cdot p+p^2 &\leq& \frac{3,8416}{639}p-\frac{3,8416}{639}p^2&\scriptsize \mid\; -\frac{3,8416}{639}p+\frac{3,8416}{639}p^2\\[5pt]
p^2+\frac{3,8416}{639}p^2-2\cdot0,0391\cdot p-\frac{3,8416}{639}p+0,0391^2 &\leq& 0&\scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/853d94a5bce3bafafcb2fe23eb2e0289cd67d4cad244b7fdb77860247c11479c_light.svg) Fasse den Ausdruck links vom Gleichheitszeichen als Funktionsterm
Fasse den Ausdruck links vom Gleichheitszeichen als Funktionsterm  einer Funktion
einer Funktion  auf. Der Graph von
auf. Der Graph von  ist eine nach oben geöffnete Parabel.
Diese Ungleichung kannst du nun mit dem solve-Befehl des CAS nach
ist eine nach oben geöffnete Parabel.
Diese Ungleichung kannst du nun mit dem solve-Befehl des CAS nach  umformen. So erhältst du das gesuchte Intervall.
umformen. So erhältst du das gesuchte Intervall.
Das CAS liefert dir die folgenden Grenzen für :
:  .
.
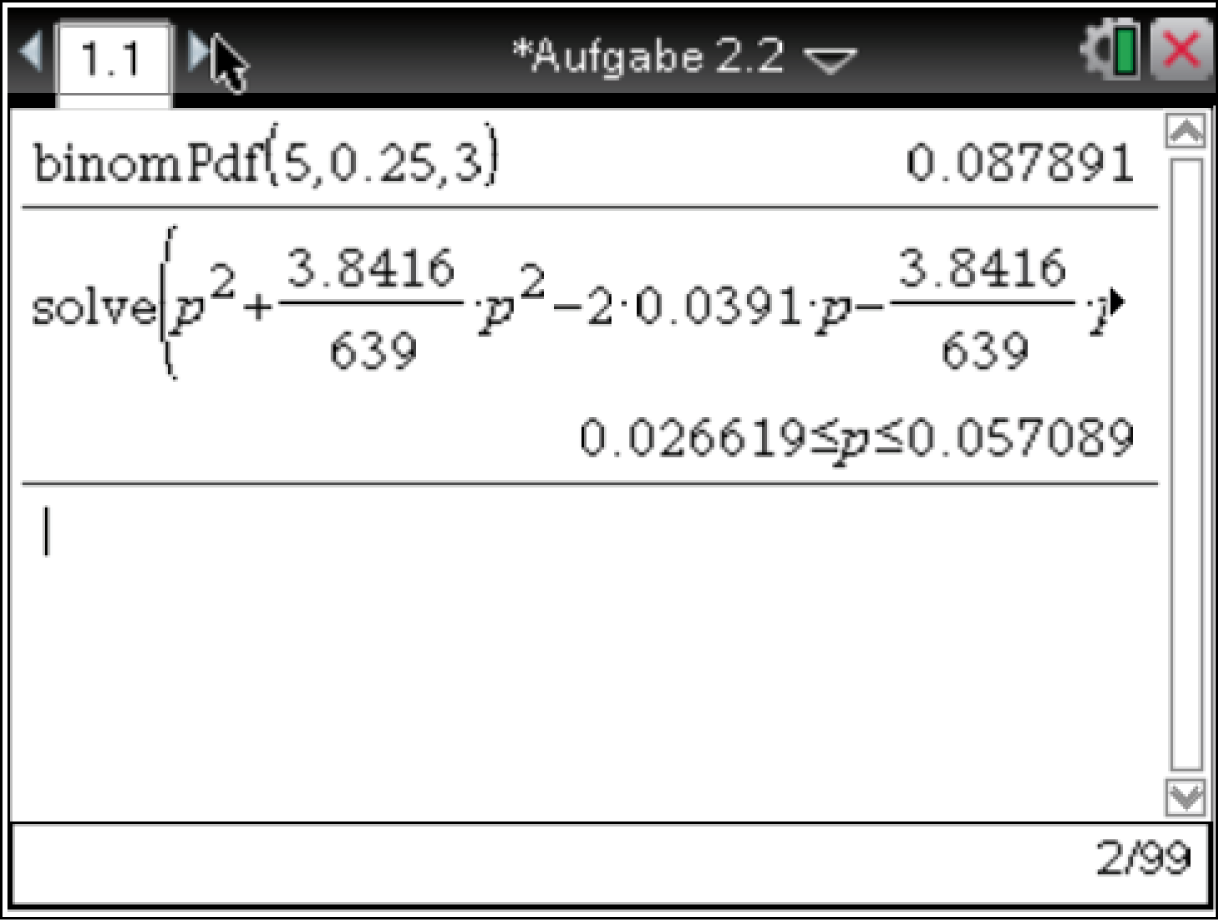 Damit folgt: der tatsächliche Anteil
Damit folgt: der tatsächliche Anteil  der markierten Fische liegt mit einer Wahrscheinlichkeit von 95 % im Intervall
der markierten Fische liegt mit einer Wahrscheinlichkeit von 95 % im Intervall ![\( [0,0266\,;\,0,0571]\)](https://www.schullv.de/resources/formulas/b99e3618e6c907f2f6779ba79b8cb20bfb762c835afd04b9758ced553e5f95e1_light.svg) .
4. Schritt: Aussage des Präsidenten überprüfen
Wenn nun der Präsident des Angelvereins Recht hat, so darf der Anteil der markierten Fische höchstens
.
4. Schritt: Aussage des Präsidenten überprüfen
Wenn nun der Präsident des Angelvereins Recht hat, so darf der Anteil der markierten Fische höchstens  betragen.
Dieser Wert liegt innerhalb des Vertrauensintervalls. Der Präsident könnte also Recht haben.
Insgesamt ergibt sich, dass der Anteil der markierten Fische mit einer Wahrscheinlichkeit von
betragen.
Dieser Wert liegt innerhalb des Vertrauensintervalls. Der Präsident könnte also Recht haben.
Insgesamt ergibt sich, dass der Anteil der markierten Fische mit einer Wahrscheinlichkeit von  im Intervall
im Intervall ![\( [0,0266\,;\,0,0571]\)](https://www.schullv.de/resources/formulas/b99e3618e6c907f2f6779ba79b8cb20bfb762c835afd04b9758ced553e5f95e1_light.svg) liegt. Aus der Behauptung des Präsidenten des Angelvereins ergäbe sich der Anteil der markierten Fische mit höchstens
liegt. Aus der Behauptung des Präsidenten des Angelvereins ergäbe sich der Anteil der markierten Fische mit höchstens  . Dieser Wert liegt innerhalb des angegebenen Vertrauensintervalls. Daher kann die Behauptung des Präsidenten nicht widerlegt werden.
. Dieser Wert liegt innerhalb des angegebenen Vertrauensintervalls. Daher kann die Behauptung des Präsidenten nicht widerlegt werden.
Nun wird eine Stichprobe von
- Wähle die
-Regel, welche eine Aussage über ein 95\,\%-Konfidenzintervall um den Erwartungswert
macht.
- Bedenke:
. Forme den Ausdruck in der
-Regel also so um, dass er eine Aussage über
trifft. Hieraus ergibt sich:
.
- Löse die Ungleichung nach
auf und berechne so die Grenzen des Intervalls.
- Vergiss nicht, zum Schluss die Aussage des Präsidenten anhand des Vertrauensintervalls zu überprüfen.
- die relative Häufigkeit
Das CAS liefert dir die folgenden Grenzen für

a)  Wahrscheinlichkeiten berechnen
Deine Aufgabe ist es, die Wahrscheinlichkeiten zweier Ereignisse zu berechnen. Hierbei sind 15 Fische in dem betrachteten Becken, von denen 5 Fische einen Gewinnpunkt tragen, und es werden nacheinander drei Fische geangelt. Dabei handelt es sich um ein Ziehen ohne Zurücklegen. Zur Hilfe kannst du ein Baumdiagramm wie das folgende skizzieren. Dabei steht G für einen Gewinn und N für eine Niete.
Wahrscheinlichkeiten berechnen
Deine Aufgabe ist es, die Wahrscheinlichkeiten zweier Ereignisse zu berechnen. Hierbei sind 15 Fische in dem betrachteten Becken, von denen 5 Fische einen Gewinnpunkt tragen, und es werden nacheinander drei Fische geangelt. Dabei handelt es sich um ein Ziehen ohne Zurücklegen. Zur Hilfe kannst du ein Baumdiagramm wie das folgende skizzieren. Dabei steht G für einen Gewinn und N für eine Niete.
 Du kannst die gesuchten Wahrscheinlichkeiten mit Hilfe der Pfadregeln berechnen.
Du kannst die gesuchten Wahrscheinlichkeiten mit Hilfe der Pfadregeln berechnen.
Definiere dazu zunächst eine Zufallsvariable . Díe Zufallsvariable
. Díe Zufallsvariable  beschreibt die Anzahl der Gewinne.
Ereignis
beschreibt die Anzahl der Gewinne.
Ereignis  Hierbei handelt es sich um das Ereignis, dass genau zwei Gewinnfische geangelt werden. Mit Hilfe der Pfadregeln und dem Baumdiagramm ergibt sich hier:
Hierbei handelt es sich um das Ereignis, dass genau zwei Gewinnfische geangelt werden. Mit Hilfe der Pfadregeln und dem Baumdiagramm ergibt sich hier:
 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  werden genau zwei Gewinnpunkte erzielt.
Ereignis
werden genau zwei Gewinnpunkte erzielt.
Ereignis  Hierbei handelt es sich um das Ereignis, dass mindestens ein Gewinnfisch geangelt wird. Du suchst also die Wahrscheinlichkeit
Hierbei handelt es sich um das Ereignis, dass mindestens ein Gewinnfisch geangelt wird. Du suchst also die Wahrscheinlichkeit  .
.
Diese kannst du wieder mit Hilfe der Pfadregeln und des obigen Baumdiagramms berechnen. Du kannst hierbei auch den Trick des Gegenereignisses anwenden, damit du weniger Pfade addieren musst: Dann ergibt sich:
Dann ergibt sich:
 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  wird mindestens ein Gewinnpunkt erzielt.
wird mindestens ein Gewinnpunkt erzielt.

Definiere dazu zunächst eine Zufallsvariable
Diese kannst du wieder mit Hilfe der Pfadregeln und des obigen Baumdiagramms berechnen. Du kannst hierbei auch den Trick des Gegenereignisses anwenden, damit du weniger Pfade addieren musst:
b)  Aussagen ableiten
In diesem Aufgabenteil sollst du dich mit dem zweiten Becken beschäftigen. In diesem Becken wird jeder Fisch vor dem nächsten Angelversuch zurück ins Becken gelegt. Hierbei handelt es sich also um ein Ziehen mit Zurücklegen.
Aussagen ableiten
In diesem Aufgabenteil sollst du dich mit dem zweiten Becken beschäftigen. In diesem Becken wird jeder Fisch vor dem nächsten Angelversuch zurück ins Becken gelegt. Hierbei handelt es sich also um ein Ziehen mit Zurücklegen.
Du weißt hier nicht, wie viele Fische im Becken sind, und auch nicht wie hoch der Anteil der Gewinnfische ist. Dir ist der folgende Term gegeben, der die Wahrscheinlichkeit für einen einfachen Gewinn beschreibt:
 Zusätzlich ist dir noch ein zweiter Term gegeben, der die Wahrscheinlichkeit für einen Hauptgewinn darstellt:
Zusätzlich ist dir noch ein zweiter Term gegeben, der die Wahrscheinlichkeit für einen Hauptgewinn darstellt:
 Aus diesen beiden Termen sollst du nun Aussagen über die Spielregeln, sowie über den Anteil der Gewinnfische ableiten.
Du kannst dazu beide Terme getrennt betrachten. Beginne mit dem ersten Term und überlege dir, ob dich dieser Term an eine Formel erinnert, die du bereits kennst.
Mit dieser Erkenntnis kannst du dann den zweiten Term interpretieren.
1. Schritt: Ersten Term betrachten
Aus diesen beiden Termen sollst du nun Aussagen über die Spielregeln, sowie über den Anteil der Gewinnfische ableiten.
Du kannst dazu beide Terme getrennt betrachten. Beginne mit dem ersten Term und überlege dir, ob dich dieser Term an eine Formel erinnert, die du bereits kennst.
Mit dieser Erkenntnis kannst du dann den zweiten Term interpretieren.
1. Schritt: Ersten Term betrachten
 Dieser Term hat Ähnlichkeit mit der Formel für die Binomialverteilung. Ist
Dieser Term hat Ähnlichkeit mit der Formel für die Binomialverteilung. Ist  eine binomialverteilte Zufallsvariable mit den Parametern
eine binomialverteilte Zufallsvariable mit den Parametern  und
und  , so gilt:
, so gilt:
 Vergleichst du nun, den obigen Term mit dieser Formel, so kannst du davon ausgehen, dass der Term eine Wahrscheinlichkeit der Form
Vergleichst du nun, den obigen Term mit dieser Formel, so kannst du davon ausgehen, dass der Term eine Wahrscheinlichkeit der Form  für eine binomialverteilte Zufallsvariable
für eine binomialverteilte Zufallsvariable  beschreibt. Die Parameter kannst du dabei ablesen, sodass du erhältst:
beschreibt. Die Parameter kannst du dabei ablesen, sodass du erhältst:
 ,
,  und
und  Da es sich im gegebenen Sachverhalt um ein Ziehen mit Zurücklegen handelt und nur zwei Merkmalsausprägungen unterschieden werden, kannst du nun diese Erkenntnisse auf den Sachzusammenhang übertragen.
Nimmst du
Da es sich im gegebenen Sachverhalt um ein Ziehen mit Zurücklegen handelt und nur zwei Merkmalsausprägungen unterschieden werden, kannst du nun diese Erkenntnisse auf den Sachzusammenhang übertragen.
Nimmst du  als Wahrscheinlichkeit dafür, einen Gewinnfisch zu angeln , und
als Wahrscheinlichkeit dafür, einen Gewinnfisch zu angeln , und  als Anzahl der Angelversuche an, so kannst du den obigen Term als Wahrscheinlichkeit dafür in fünf Versuchen vier Gewinnpunkte zu erzielen interpretieren.
als Anzahl der Angelversuche an, so kannst du den obigen Term als Wahrscheinlichkeit dafür in fünf Versuchen vier Gewinnpunkte zu erzielen interpretieren.
Daran kannst du auch erkennen, dass ein einfacher Gewinn darin besteht, in fünf Versuchen vier Gewinnpunkte zu erzielen. 2. Schritt: Zweiten Term betrachten Der zweite Term ist dir gegeben mit:
 Dieser Term beschreibt die Wahrscheinlichkeit dafür, einen Hauptgewinn zu erzielen. Du weißt bereits, dass in diesem Spiel fünfmal geangelt wird und der Anteil der Gewinnfische
Dieser Term beschreibt die Wahrscheinlichkeit dafür, einen Hauptgewinn zu erzielen. Du weißt bereits, dass in diesem Spiel fünfmal geangelt wird und der Anteil der Gewinnfische  beträgt. Daraus kannst du ableiten, dass der hier betrachtete Term die Wahrscheinlichkeit beschreibt, dass in fünf Versuchen genau fünf Gewinnfische geangelt werden.
beträgt. Daraus kannst du ableiten, dass der hier betrachtete Term die Wahrscheinlichkeit beschreibt, dass in fünf Versuchen genau fünf Gewinnfische geangelt werden.
Der Hauptgewinn besteht also darin in fünf Versuchen fünf Fische mit einem Gewinnpunkt zu angeln. Insgesamt lässt sich aus den beiden Termen also folgendes ableiten: Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, genau drei Gewinnpunkte zu erzielen. Oben hast du die Formel für die Binomialverteilung bereits gesehen und weißt, dass solche Wahrscheinlichkeiten mit dieser berechnet werden können. Betrachtest du hier die Zufallsvariable
Wahrscheinlichkeit berechnen
Hier sollst du nun die Wahrscheinlichkeit dafür berechnen, genau drei Gewinnpunkte zu erzielen. Oben hast du die Formel für die Binomialverteilung bereits gesehen und weißt, dass solche Wahrscheinlichkeiten mit dieser berechnet werden können. Betrachtest du hier die Zufallsvariable  , die die zufällige Anzahl der Fische mit Gewinnpunkten beschreibt, so ist
, die die zufällige Anzahl der Fische mit Gewinnpunkten beschreibt, so ist  binomialverteilt mit den Parametern
binomialverteilt mit den Parametern  und
und  . Du suchst hier also
. Du suchst hier also  .
.
Diese kannst du handschriftlich mit der obigen Formel für die Binomialverteilung berechnen, oder auch mit dem CAS. Lösungsweg A: Formel für die Binomialverteilung
Lösungsweg A: Formel für die Binomialverteilung

 Lösungsweg B: CAS
Hierbei kannst du den binompdf-Befehl des CAS verwenden. Diesen findest du im Statistik unter:
Lösungsweg B: CAS
Hierbei kannst du den binompdf-Befehl des CAS verwenden. Diesen findest du im Statistik unter:
 ,
,  und
und  ein, so erhältst du das folgende Ergebnis:
ein, so erhältst du das folgende Ergebnis:

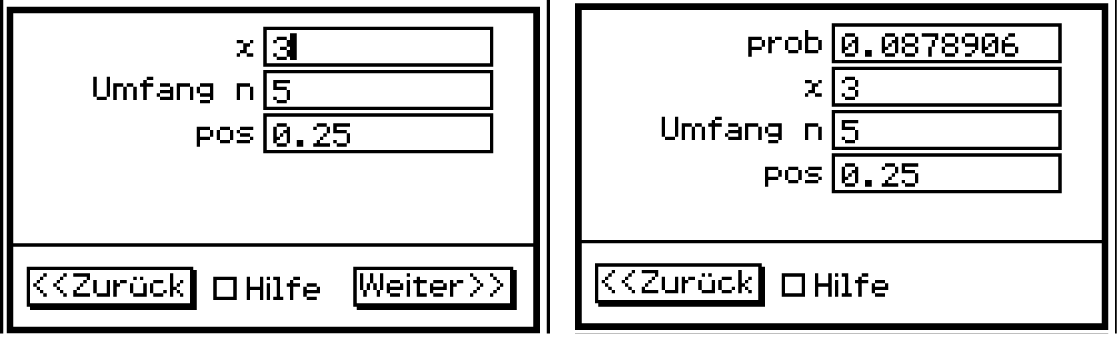 Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  werden in diesem Spiel genau drei Gewinnpunkte erzielt.
werden in diesem Spiel genau drei Gewinnpunkte erzielt.
Du weißt hier nicht, wie viele Fische im Becken sind, und auch nicht wie hoch der Anteil der Gewinnfische ist. Dir ist der folgende Term gegeben, der die Wahrscheinlichkeit für einen einfachen Gewinn beschreibt:
Daran kannst du auch erkennen, dass ein einfacher Gewinn darin besteht, in fünf Versuchen vier Gewinnpunkte zu erzielen. 2. Schritt: Zweiten Term betrachten Der zweite Term ist dir gegeben mit:
Der Hauptgewinn besteht also darin in fünf Versuchen fünf Fische mit einem Gewinnpunkt zu angeln. Insgesamt lässt sich aus den beiden Termen also folgendes ableiten:
- Der Anteil der Fische mit Gewinnpunkt liegt bei
.
- Es wird fünfmal geangelt.
- Werden vier Gewinnpunkte erzielt, so gibt es einen einfachen Gewinn.
- Werden fünf Gewinnpunkte erzielt, so gibt es einen Hauptgewinn.
Diese kannst du handschriftlich mit der obigen Formel für die Binomialverteilung berechnen, oder auch mit dem CAS.
CALC  Verteilung
Verteilung  Binom. Einzelwkt.
Binom. Einzelwkt.
Gibst du dort die entsprechenden Parameter 
c)  Behauptung des Präsidenten mit Hilfe eines Vertrauensintervalls untersuchen
In diesem Aufgabenteil geht es nun um einen See. Der Präsident des Angelvereins behauptet, dass in diesem See mindestens
Behauptung des Präsidenten mit Hilfe eines Vertrauensintervalls untersuchen
In diesem Aufgabenteil geht es nun um einen See. Der Präsident des Angelvereins behauptet, dass in diesem See mindestens  Fische leben. Um die tatsächliche Anzahl der Fische zu schätzen wurden
Fische leben. Um die tatsächliche Anzahl der Fische zu schätzen wurden  Fische gefangen, markiert und wieder zurückgelegt.
Fische gefangen, markiert und wieder zurückgelegt.
Nun wird eine Stichprobe von Fischen entnommen. Davon sind
Fischen entnommen. Davon sind  Fische markiert. Anhand dieser Stichprobe sollst du nun ein Vertrauensintervall mit einer Vertrauenswahrscheinlichkeit von
Fische markiert. Anhand dieser Stichprobe sollst du nun ein Vertrauensintervall mit einer Vertrauenswahrscheinlichkeit von  aufstellen, und so überprüfen, ob die Behauptung des Präsidenten widerlegt werden kann.
Wenn der Präsident Recht hat, dann darf der Anteil
aufstellen, und so überprüfen, ob die Behauptung des Präsidenten widerlegt werden kann.
Wenn der Präsident Recht hat, dann darf der Anteil  der markierten Fische höchstens
der markierten Fische höchstens  betragen. Gesucht ist nun also ein Vertrauensintervall über den Anteil der markierten Fische im See. Liegt
betragen. Gesucht ist nun also ein Vertrauensintervall über den Anteil der markierten Fische im See. Liegt  innerhalb dieses Intervalls, so kann nicht ausgeschlossen werden, dass der Präsident Recht hat, andernfalls, kann davon ausgegangen werden, dass der Präsident mit seiner Behauptung falsch liegt.
Das Vertrauensintervall wird dabei ausgehend von der Stichprobe mit
innerhalb dieses Intervalls, so kann nicht ausgeschlossen werden, dass der Präsident Recht hat, andernfalls, kann davon ausgegangen werden, dass der Präsident mit seiner Behauptung falsch liegt.
Das Vertrauensintervall wird dabei ausgehend von der Stichprobe mit  Fischen, von denen
Fischen, von denen  markiert sind, bestimmt.
Das Vertrauensintervall soll sich auf den Anteil
markiert sind, bestimmt.
Das Vertrauensintervall soll sich auf den Anteil  der Fische im See beziehen, der in diesem Fall unbekannt ist. Einen ersten Schätzwert für
der Fische im See beziehen, der in diesem Fall unbekannt ist. Einen ersten Schätzwert für  kannst du über die Angabe ermitteln, dass von
kannst du über die Angabe ermitteln, dass von  Fischen
Fischen  markiert sind:
markiert sind:
 .
Gesucht ist nun ein Intervall, in dem der tatsächliche Anteil
.
Gesucht ist nun ein Intervall, in dem der tatsächliche Anteil  der markierten Fische mit einer Wahrscheinlichkeit von 95 % liegt. Einen Ansatz für dieses Problem bieten die
der markierten Fische mit einer Wahrscheinlichkeit von 95 % liegt. Einen Ansatz für dieses Problem bieten die  -Regeln.
Du kannst also so vorgehen:
-Regeln.
Du kannst also so vorgehen:
 -Regel auswählen
Du findest die Regel
-Regel auswählen
Du findest die Regel
 2. Schritt: Ausdruck umformen
Betrachte nur den Ausdruck in Klammern und forme ihn so um, dass er eine Aussage über
2. Schritt: Ausdruck umformen
Betrachte nur den Ausdruck in Klammern und forme ihn so um, dass er eine Aussage über  macht. Du kennst bereits:
macht. Du kennst bereits:
![\(\begin{array}{rrrl}
\mu-1,96\sigma &\leq & X &\leq& \mu+1,96\sigma&\scriptsize \mid\; \mu=n\cdot p\\[5pt]
n\cdot p-1,96\sigma &\leq & X &\leq& n\cdot p+1,96\sigma&\scriptsize \mid\; \sigma=\sqrt{n\cdot p\cdot (1-p)}\\[5pt]
n\cdot p-1,96\cdot\sqrt{n\cdot p\cdot (1-p)} &\leq& X &\leq& n\cdot p+1,96\sqrt{n\cdot p\cdot (1-p)}&\scriptsize \mid\; :n\\[5pt]
p-1,96\cdot\sqrt{\frac{p\cdot (1-p)}{n}} &\leq& \frac{X}{n} &\leq& p+1,96\sqrt{\frac{p\cdot (1-p)}{n}}&\scriptsize \mid\; -p\\[5pt]
-1,96\cdot\sqrt{\frac{p\cdot (1-p)}{n}} &\leq& \frac{X}{n}-p &\leq& 1,96\sqrt{\frac{p\cdot (1-p)}{n}}\\[5pt]
\left|\frac{X}{n}-p\right| &\leq& 1,96\sqrt{\frac{p\cdot (1-p)}{n}}&&&\scriptsize \mid\; \frac{X}{n}=0,0391;\qquad n=639\\[5pt]
\left|0,0391-p\right| &\leq& 1,96\sqrt{\frac{p\cdot (1-p)}{639}}&\scriptsize \\
\end{array}\)](https://www.schullv.de/resources/formulas/6f68ef648fac6451f5977686a90a8cb1454589948c5b9a0658a507ff81e113d3_light.svg) 3. Schritt: Ungleichung lösen
Du kannst auf beiden Seiten quadrieren und die Ungleichung nach
3. Schritt: Ungleichung lösen
Du kannst auf beiden Seiten quadrieren und die Ungleichung nach  auflösen.
auflösen.
![\(\begin{array}{rll}
\left|0,0391-p\right| &\leq& 1,96\sqrt{\frac{p\cdot (1-p)}{639}}&\scriptsize \mid\; (\;)^2\\[5pt]
(0,0391-p)^2 &\leq& (1,96)^2\cdot\frac{p\cdot(1-p)}{639}&\scriptsize \\[5pt]
0,0391^2-2\cdot0,0391\cdot p+p^2 &\leq& \frac{3,8416}{639}\cdot p\cdot(1-p)&\scriptsize \\[5pt]
0,0391^2-2\cdot0,0391\cdot p+p^2 &\leq& \frac{3,8416}{639}p-\frac{3,8416}{639}p^2&\scriptsize \mid\; -\frac{3,8416}{639}p+\frac{3,8416}{639}p^2\\[5pt]
p^2+\frac{3,8416}{639}p^2-2\cdot0,0391\cdot p-\frac{3,8416}{639}p+0,0391^2 &\leq& 0&\scriptsize \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/20b3bd347f6ddd9619f1ddbaea98beb9ce7cf12961974bbb41c976b8d6d00bd9_light.svg) Fasse den Ausdruck links vom Gleichheitszeichen als Funktionsterm
Fasse den Ausdruck links vom Gleichheitszeichen als Funktionsterm  einer Funktion
einer Funktion  auf. Der Graph von
auf. Der Graph von  ist eine nach oben geöffnete Parabel.
Diese Ungleichung kannst du nun mit dem solve-Befehl im Main-Menu des CAS nach
ist eine nach oben geöffnete Parabel.
Diese Ungleichung kannst du nun mit dem solve-Befehl im Main-Menu des CAS nach  umformen. So erhältst du das gesuchte Intervall.
umformen. So erhältst du das gesuchte Intervall.
Das CAS liefert dir die folgenden Grenzen für :
:  .
.
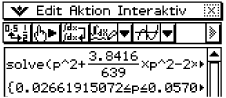 Damit folgt: der tatsächliche Anteil
Damit folgt: der tatsächliche Anteil  der markierten Fische liegt mit einer Wahrscheinlichkeit von 95 % im Intervall
der markierten Fische liegt mit einer Wahrscheinlichkeit von 95 % im Intervall ![\([0,0266\,;\,0,0571]\)](https://www.schullv.de/resources/formulas/df1f5ee26d5ca340e2220c41a46760ed1316e4c98c9c1e0f55cbf4ff5f982981_light.svg) .
4. Schritt: Aussage des Präsidenten überprüfen
Wenn nun der Präsident des Angelvereins Recht hat, so darf der Anteil der markierten Fische höchstens
.
4. Schritt: Aussage des Präsidenten überprüfen
Wenn nun der Präsident des Angelvereins Recht hat, so darf der Anteil der markierten Fische höchstens  betragen.
Dieser Wert liegt innerhalb des Vertrauensintervalls. Der Präsident könnte also Recht haben.
Insgesamt ergibt sich, dass der Anteil der markierten Fische mit einer Wahrscheinlichkeit von
betragen.
Dieser Wert liegt innerhalb des Vertrauensintervalls. Der Präsident könnte also Recht haben.
Insgesamt ergibt sich, dass der Anteil der markierten Fische mit einer Wahrscheinlichkeit von  im Intervall
im Intervall ![\([0,0266\,;\,0,0571]\)](https://www.schullv.de/resources/formulas/df1f5ee26d5ca340e2220c41a46760ed1316e4c98c9c1e0f55cbf4ff5f982981_light.svg) liegt. Aus der Behauptung des Präsidenten des Angelvereins ergäbe sich der Anteil der markierten Fische mit höchstens
liegt. Aus der Behauptung des Präsidenten des Angelvereins ergäbe sich der Anteil der markierten Fische mit höchstens  . Dieser Wert liegt innerhalb des angegebenen Vertrauensintervalls. Daher kann die Behauptung des Präsidenten nicht widerlegt werden.
. Dieser Wert liegt innerhalb des angegebenen Vertrauensintervalls. Daher kann die Behauptung des Präsidenten nicht widerlegt werden.
Nun wird eine Stichprobe von
- Wähle die
-Regel, welche eine Aussage über ein 95\,\%-Konfidenzintervall um den Erwartungswert
macht.
- Bedenke:
. Forme den Ausdruck in der
-Regel also so um, dass er eine Aussage über
trifft. Hieraus ergibt sich:
.
- Löse die Ungleichung nach
auf und berechne so die Grenzen des Intervalls.
- Vergiss nicht, zum Schluss die Aussage des Präsidenten anhand des Vertrauensintervalls zu überprüfen.
- die relative Häufigkeit
Das CAS liefert dir die folgenden Grenzen für
