Aufgabe 1B
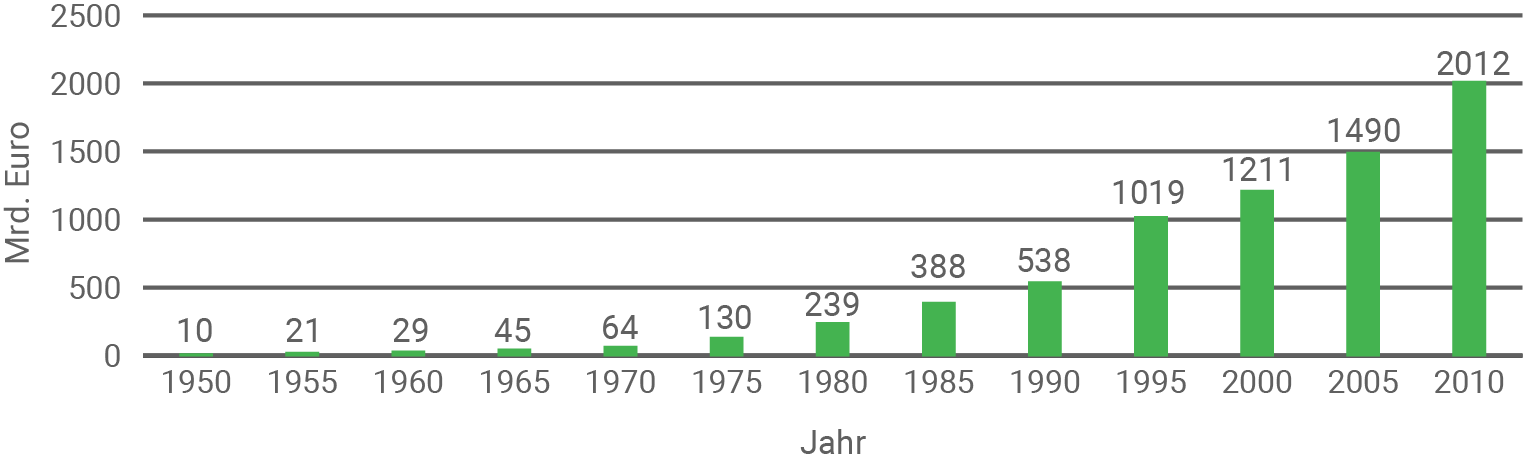
Die Grafik zeigt die Schulden Deutschlands zu Beginn eines Jahres für die Jahre 1950 bis 2010 in Mrd. Euro.
 definierte Funktion
definierte Funktion  mit
mit  beschreibt für
beschreibt für  näherungsweise die Schulden Deutschlands von 1950 bis 2010. Dabei gibt
näherungsweise die Schulden Deutschlands von 1950 bis 2010. Dabei gibt  die Zeit in Jahren seit 1950 an und
die Zeit in Jahren seit 1950 an und  die Schulden in Mrd. Euro.
die Schulden in Mrd. Euro.
 durch die auf ganz
durch die auf ganz  definierte Funktion
definierte Funktion  mit
mit  beschrieben.
beschrieben.
Dabei gibt die Zeit in Jahren seit 2005 und
die Zeit in Jahren seit 2005 und  die momentane Änderungsrate der Schulden in Mrd. Euro pro Jahr an.
die momentane Änderungsrate der Schulden in Mrd. Euro pro Jahr an.
 Jahre nach dem Jahr 2005 für
Jahre nach dem Jahr 2005 für  betrachtet.
betrachtet.

a)
Gib die beiden Fünfjahreszeiträume an, in denen sich die Schulden mindestens verdoppelt haben.
(2 BE)
b)
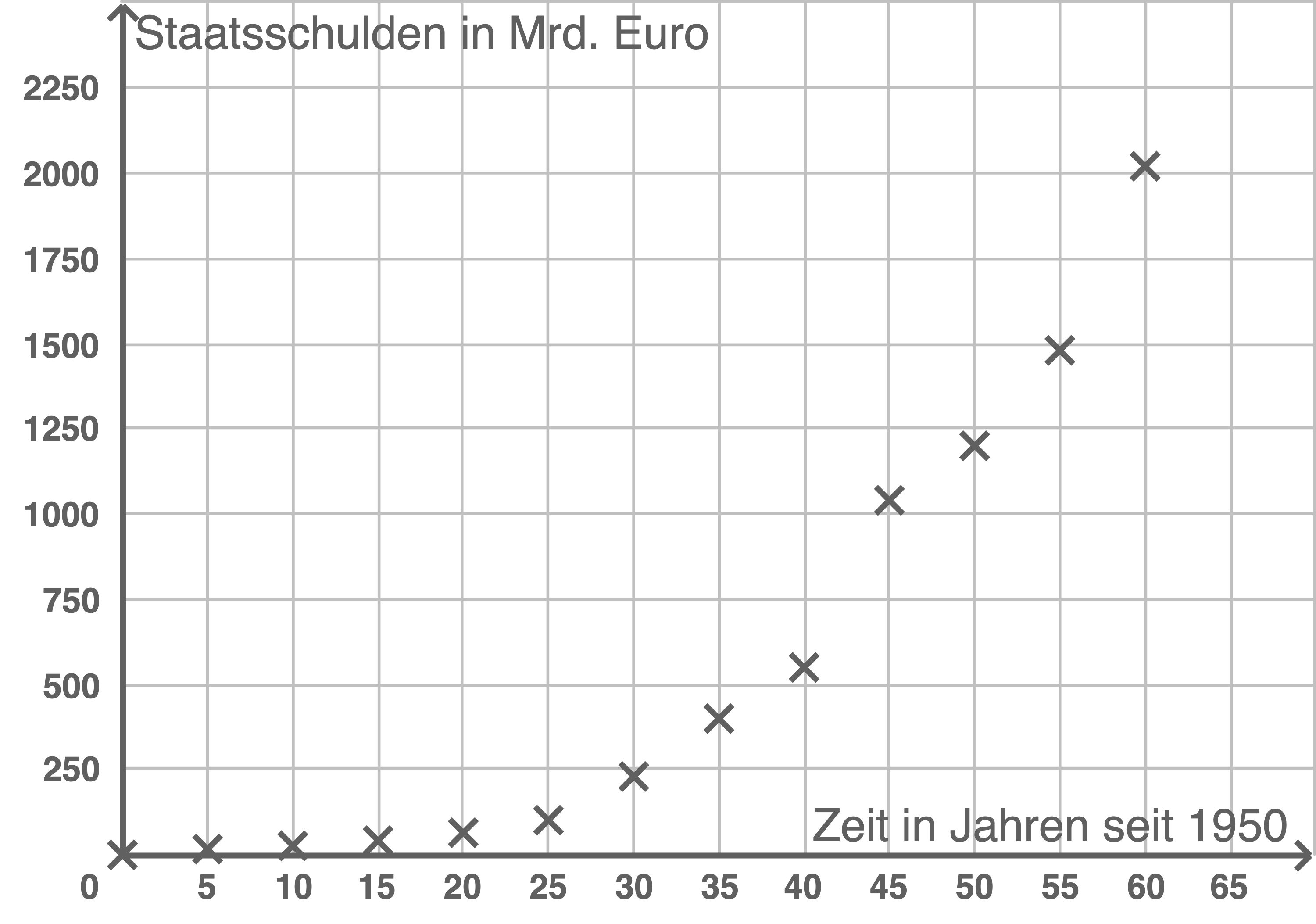
Gib ein Verfahren an zur Bestimmung einer Funktion, die für den Zeitraum von 1950 bis 2010 die Schulden in Abhängigkeit von der Zeitdauer seit 1950 näherungsweise beschreibt. Nenne drei Schritte der Durchführung des Verfahrens.
In der nebenstehenden Abbildung sind die Daten aus der Grafik eingetragen. Die auf ganz
(4 BE)

c)
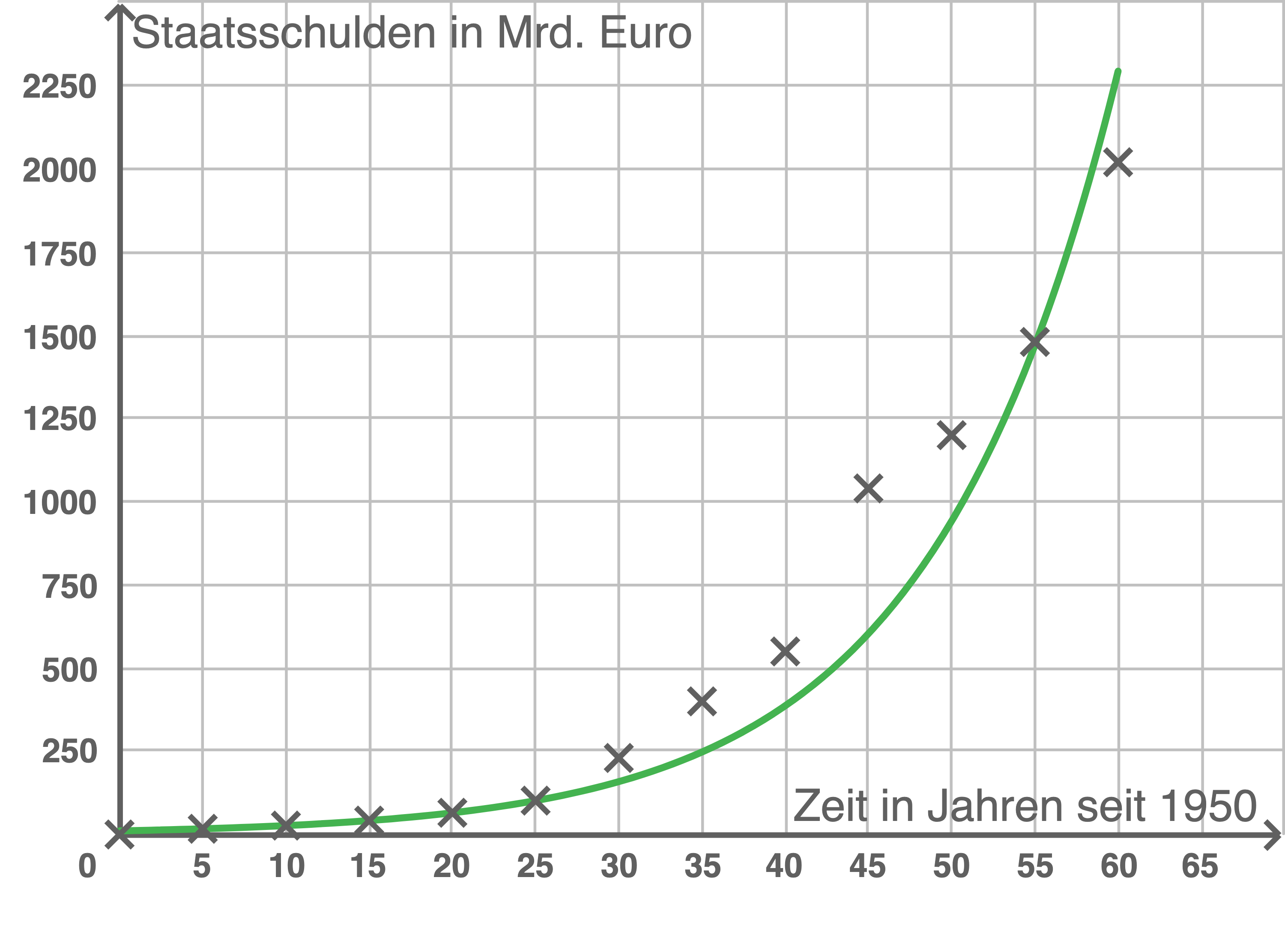
Zeichne den Graphen von  in die Abbildung.
in die Abbildung.
(3 BE)
d)
Bestimme mithilfe der Funktion  die jährliche prozentuale Zunahme der Schulden.
die jährliche prozentuale Zunahme der Schulden.
Untersuche, ob es einen Zeitpunkt gibt, zu dem die momentane Änderungsrate der Schulden größer als 250 Mrd. Euro pro Jahr ist.
Im Folgenden wird in einem anderen Modell die momentane Änderungsrate der Schulden Deutschlands zu Beginn eines Jahres ab dem Jahr 2005 betrachtet. Sie wird für Untersuche, ob es einen Zeitpunkt gibt, zu dem die momentane Änderungsrate der Schulden größer als 250 Mrd. Euro pro Jahr ist.
(5 BE)
Dabei gibt
e)
Begründe, dass in der Modellierung mit  die momentane Änderungsrate der Schulden ab Beginn des Jahres 2005 abnimmt.
die momentane Änderungsrate der Schulden ab Beginn des Jahres 2005 abnimmt.
Berechne das Jahr, in dem die Schulden ihren Höchststand erreichen.
Im Folgenden werden die zu erwartenden Schulden Deutschlands Berechne das Jahr, in dem die Schulden ihren Höchststand erreichen.
(6 BE)
f)
Begründe, dass sich die zu erwartenden Schulden zu Beginn des Jahres  mithilfe des folgenden Terms berechnen lassen:
mithilfe des folgenden Terms berechnen lassen:  Bestimme das Jahr, in dem die Schulden vollständig abgebaut sind.
Bestimme das Jahr, in dem die Schulden vollständig abgebaut sind.
(7 BE)
g)
Begründe, dass die Lösungen der Gleichung  Zeitpunkte nach dem Jahr 2005 angeben, zu denen die Schulden um
Zeitpunkte nach dem Jahr 2005 angeben, zu denen die Schulden um  der vorhandenen Schulden wachsen.
der vorhandenen Schulden wachsen.
Bestimme den Zeitraum, in dem die momentane Änderungsrate der Schulden weniger als der Schulden beträgt.
der Schulden beträgt.
Bestimme den Zeitraum, in dem die momentane Änderungsrate der Schulden weniger als
(8 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
1950 bis 1955 und 1970 bis 1975
b)
Ein geeignetes Verfahren ist die Regression. Hierbei müssen folgende drei Schritte durchgeführt werden:
- Auswahl des Funktionstyps
- Eingabe aller Wertepaare in den Taschenrechner
- Bestimmung des Funktionsterms
c)
d)
Die jährliche prozentuale Zunahme der Schulden lässt sich wie folgt berechnen:
Die Schulden nehmen jährlich um etwa  zu.
Da
zu.
Da  exponentielles Wachstum beschreibt, erreicht
exponentielles Wachstum beschreibt, erreicht  sein Maximum am rechten Rand des Definitionsbereichs. Es gilt:
sein Maximum am rechten Rand des Definitionsbereichs. Es gilt:  Folglich gibt es keinen Zeitpunkt, zu dem die momentane Änderungsrate der Schulden größer als 250 Mrd. Euro pro Jahr ist.
Folglich gibt es keinen Zeitpunkt, zu dem die momentane Änderungsrate der Schulden größer als 250 Mrd. Euro pro Jahr ist.
e)
Wegen  und
und  beschreibt der Term
beschreibt der Term  eine exponentielle Abnahme. Somit ist
eine exponentielle Abnahme. Somit ist  monoton fallend.
monoton fallend.
 hat die Lösung
hat die Lösung  mit
mit  Der Höchststand der Schulden wird also im Verlauf des Jahres 2012 erreicht.
Der Höchststand der Schulden wird also im Verlauf des Jahres 2012 erreicht.
f)
Da  die momentane Änderungsrate der Schulden ab 2005 beschreibt, lassen sich mit
die momentane Änderungsrate der Schulden ab 2005 beschreibt, lassen sich mit  die seit Beginn des Jahres 2005 im Zeitraum von
die seit Beginn des Jahres 2005 im Zeitraum von  Jahren insgesamt hinzugekommenen Schulden berechnen. Der Summand 1490 beschreibt die im Jahr 2005 bereits vorhandenen Schulden, sodass sich als Summe die Schulden im Jahr
Jahren insgesamt hinzugekommenen Schulden berechnen. Der Summand 1490 beschreibt die im Jahr 2005 bereits vorhandenen Schulden, sodass sich als Summe die Schulden im Jahr  ergeben.
ergeben.
 besitzt die positive Lösung
besitzt die positive Lösung  mit
mit  . Im Verlauf des Jahres 2070 sind die Schulden vollständig abgebaut.
. Im Verlauf des Jahres 2070 sind die Schulden vollständig abgebaut.
g)
Der Quotient beschreibt den Anteil der momentanen Änderungsrate der Schulden im Jahr  nach 2005 an den Schulden im Jahr
nach 2005 an den Schulden im Jahr  nach 2005. Damit sind die Lösungen der Gleichung die Zeitpunkte nach dem Jahr 2005, zu denen dieser Anteil
nach 2005. Damit sind die Lösungen der Gleichung die Zeitpunkte nach dem Jahr 2005, zu denen dieser Anteil  beträgt.
beträgt.
 wird mit dem solve-Befehl des Taschenrechners gelöst und besitzt im betrachteten Zeitraum die Lösung
wird mit dem solve-Befehl des Taschenrechners gelöst und besitzt im betrachteten Zeitraum die Lösung  mit
mit  Wegen
Wegen  für
für  ist
ist  der Anfang des gesuchten Zeitraums.
der Anfang des gesuchten Zeitraums.
 besitzt die Lösung
besitzt die Lösung  mit
mit  .
Somit ist
.
Somit ist  das Ende des gesuchten Zeitraums. Der gesuchte Zeitraum beginnt im Jahr 2007 und endet im Jahr 2050.
das Ende des gesuchten Zeitraums. Der gesuchte Zeitraum beginnt im Jahr 2007 und endet im Jahr 2050.