Aufgabe 2B
Aufgabe 2B
Es werden Kühe einer neuen Züchtung betrachtet. Bei zehn Prozent der Kühe enthält die Milch einen Inhaltsstoff, der sich mithilfe einer Untersuchung eindeutig nachweisen lässt. Dabei wird pro Kuh immer genau eine Milchprobe entnommen.
a)
Die Milchproben von  Kühen werden untersucht. Die Zufallsgröße
Kühen werden untersucht. Die Zufallsgröße  gibt die Anzahl der Kühe an, in deren Milch dieser Inhaltsstoff enthalten ist, und kann als binomialverteilt angenommen werden.
Bestimme die Wahrscheinlichkeit dafür, dass von den untersuchten Milchproben genau
gibt die Anzahl der Kühe an, in deren Milch dieser Inhaltsstoff enthalten ist, und kann als binomialverteilt angenommen werden.
Bestimme die Wahrscheinlichkeit dafür, dass von den untersuchten Milchproben genau  den Inhaltsstoff enthalten.
Bestimme die Wahrscheinlichkeit dafür, dass höchstens
den Inhaltsstoff enthalten.
Bestimme die Wahrscheinlichkeit dafür, dass höchstens  der untersuchten Milchproben den Inhaltstoff enthalten.
Ermittle das kleinste um den Erwartungswert von
der untersuchten Milchproben den Inhaltstoff enthalten.
Ermittle das kleinste um den Erwartungswert von  symmetrische Intervall mit ganzzahligen Grenzen
symmetrische Intervall mit ganzzahligen Grenzen  und
und  , für das gilt:
, für das gilt:
 .
.
(8P)
b)
Die Milchproben mehrerer Kühe werden nun nach folgendem Verfahren untersucht:
Jeder Milchprobe wird ein Teil entnommen. Diese Teile werden gemischt und das Gemisch wird auf den Inhaltsstoff untersucht. Wird der Inhaltsstoff aufgefunden, werden die Milchproben aller Kühe einzeln untersucht.
Die Anzahl der Kühe, deren Milch den Inhaltsstoff enthält, kann weiterhin als binomialverteilte Zufallsgröße angenommen werden.
Bestimme für die Milchproben von  Kühen
Kühen
- die Wahrscheinlichkeit dafür, dass das Gemisch den Inhaltsstoff enthält,
- die zu erwartende Anzahl an Untersuchungen.
(9P)
a)
Menu  Statistik
Statistik  Verteilungen
Verteilungen  Binomial Pdf
Binomial Pdf
 Abb. 1: Binomialverteilung berechnen
Abb. 1: Binomialverteilung berechnen
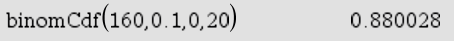 Abb. 2: Kummulierte Wahrscheinlichkeit berechnen
Abb. 2: Kummulierte Wahrscheinlichkeit berechnen
b)
Menü  Algebra
Algebra  Numerisch Lösen
Numerisch Lösen
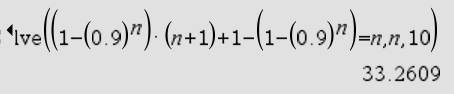 Abb. 3: Gleichung lösen
Abb. 3: Gleichung lösen
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
Interaktiv  Verteilungsfunktionen
Verteilungsfunktionen  Diskret
Diskret  binomialPDf
binomialPDf
 Abb. 1: Binomialverteilung berechnen
Abb. 1: Binomialverteilung berechnen
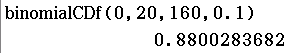 Abb. 2: Kummulierte Wahrscheinlichkeit berechnen
Abb. 2: Kummulierte Wahrscheinlichkeit berechnen
b)
Interaktive  Weiterführend
Weiterführend  solve
solve
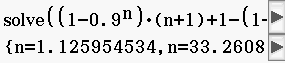 Abb. 3: Gleichung lösen
Abb. 3: Gleichung lösen
© 2016 - SchulLV.
© 2016 - SchulLV.