Aufgabe 3B

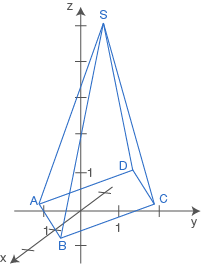
Von einer Pyramide sind folgende Eckpunkte gegeben:

$A(2\mid0\mid1)$ , $B(4\mid2\mid1)$ , $C(2\mid4\mid1)$ und $S(2\mid2\mid6)$ .

$\,$

3D-Diagramm eines geometrischen Körpers mit den Punkten A, B, C, D und S in einem Koordinatensystem.

Abb. 1: Pyramide mit Eckpunkten $A$ , $B$ , $C$ , $D$ und $S$

Zeige: Das Dreieck $ABC$ ist gleichschenklig und rechtwinklig mit dem rechten Winkel im Punkt $B$ .
Berechne die Koordinaten des vierten Punktes $D$ so, dass $A$ , $B$ , $C$ und $D$ Eckpunkte eines Quadrats sind.

(6P)

Zeige, dass es Punkte $S_{z}(2\mid2\mid z)$ es gibt, dass das jeweilige Dreieck $ACS_{z}$ ein rechtwinkliges Dreieck mit dem rechten Winkel bei $S_{z}$ ist.

(4P)

Die Punkte $B$ , $C$ und $S$ liegen in einer Ebene $E$ .
Zeige, dass es in der Ebene $E$ einen Punkt gibt, der drei gleiche Koordinaten hat und gib dessen Koordinaten an.
Untersuche, ob jede beliebige Ebene einen Punkt hat, der drei gleiche Koordinaten hat.

(7P)

Bildnachweise [nach oben]

[1]

$\blacktriangleright$ Zeigen, dass das Dreieck $\boldsymbol{ABC}$ gleischenklig ist

Ein Dreieck ist gleichschenklig, wenn zwei der drei Seiten gleich lang sind. Bilde als erstes die Verbindungsvektoren $\overrightarrow{AB}$ , $\overrightarrow{BC}$ und $\overrightarrow{CA}$ . Die Länge eines Vektors ist gerade der Betrag des Vektors. Den Betrag des Vektors kannst du mit deinem Taschenrechner berechnen.

$\overrightarrow{AB} = \pmatrix{4-2 \\ 2-0 \\ 1-1} = \pmatrix{2 \\2 \\ 0}$

$\overrightarrow{BC} = \pmatrix{2-4 \\ 4-2 \\ 1-1} = \pmatrix{-2 \\2 \\ 0}$

$\overrightarrow{CA}=\pmatrix{2-2 \\ 0-4 \\ 1-1}= \pmatrix{0 \\-4 \\ 0}$

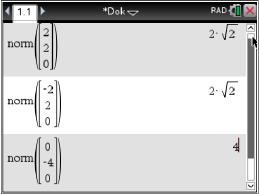Mathematische Berechnungen zur Norm von Vektoren in einem Grafikfenster.

Abb. 1: Betrag der Vektoren berechnen

Aus $|\overrightarrow{AB}| = |\overrightarrow{BC}|$ folgt, dass die beiden Vektoren $\overrightarrow{AB}$ und $\overrightarrow{BC}$ gleich lang sind. Somit hast du gezeigt, dass das Dreieck $ABC$ gleichschenklig ist.

$\blacktriangleright$ Zeige, dass das Dreieck am Punkt $\boldsymbol{B}$ einen rechten Winkel hat

Das Dreieck besitzt im Punkt $B$ einen rechten Winkel, wenn die beiden Vektoren $\overrightarrow{AB}$ und $\overrightarrow{BC}$ senkrecht zueinander stehen. Das Skalarprodukt der Vektoren $\overrightarrow{AB}$ und $\overrightarrow{BC}$ muss somit null sein.

$\overrightarrow{AB} {\circ} \overrightarrow{BC}$

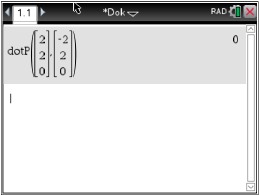Mathematik-Software mit einer Matrix und einem Eingabefeld für Berechnungen.

Abb. 2: Skalarprodukt berechnen

Da das Skalarprodukt null ist, stehen die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{BC}$ senkrecht aufeinander. Das Dreieck $ABC$ hat im Punkt $B$ einen rechten Winkel.

$\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{D}$ berechnen

In dieser Aufgabe sollst du die Koordinaten des Punktes $D$ berechnen, sodass die Punkte $A$ , $B$ , $C$ und $D$ die Eckpunkte eines Quadrates sind.

Um das Dreieck zu einem Quadrat zu ergänzen, kannst du den Vektor $\overrightarrow{BC}$ an den Ortsvektor, der zum Punkt $A$ zeigt addieren.

$\overrightarrow{OD}= \pmatrix{0 \\2 \\ 1}$

Vollständige Lösung anzeigen

Die Koordinaten des gesuchten Punktes $D$ kannst du jetzt ablesen.

Die Koordinaten des vierten Punktes sind $D(\;0 \;|\; 2 \;|\; 1 \;)$ .

$\blacktriangleright$ Winkel zwischen der Streck $\boldsymbol{\overline{AS}}$ und der Diagonalen $\boldsymbol{\overline{AC}}$ berechnen

Den Winkel zwischen zwei Vektoren kannst du mit der Cosinus-Formel berechnen.

$\cos \alpha = \dfrac{\overrightarrow{a} {\circ} \overrightarrow{b}}{|\overrightarrow{a}| \cdot |\overrightarrow{b}| }$

Um den Winkel zwischen den beiden Strecken zu berechnen, bildest du als erstes die beiden Verbindungsvektoren $\overrightarrow{AS}$ und $\overrightarrow{AC}$ und setzt diese anschließend in die Cosinus-Formel ein.

$\overrightarrow{AS} = \pmatrix{2-2 \\ 2-0 \\ 6-1} =\pmatrix{0 \\ 2 \\ 5}$

$\overrightarrow{AC} = (-1)\cdot \overrightarrow{CA} = \pmatrix{0 \\ 4 \\ 0}$

$\begin{array}[t]{rll} \cos \alpha&=& 68,199° \end{array}$

Vollständige Lösung anzeigen

Der Winkel zwischen den Strecken $\overline{AS}$ und $\overline{AC}$ beträgt $68,12°$ .

$\blacktriangleright$ Zeigen, dass es Punkte $\boldsymbol{S_z}$ gibt, sodass das Dreieck $\boldsymbol{ACS_z}$ rechtwinklig ist

Das Dreieck $ACS_z$ besitzt im Punkt $S_z$ einen rechten Winkel, wenn das Skalarprodukt zwischen den beiden Verbindungsvektoren $\overrightarrow{AS_z}$ und $\overrightarrow{CS_z}$ null ist. Berechne als erstes die beiden Verbindungsvektoren und anschließend kannst du das Skalarprodukt der beiden Vektoren berechnen. Du erhältst eine Gleichung mit einer Variablen. Ist die Gleichung lösbar, gibt es Punkte $S_z$ , sodass das Dreieck $ACS_z$ rechtwinklig ist.

1. Schritt: Verbindungsvektoren berechnen

$\overrightarrow{AS_z}= \pmatrix{2-2 \\ 2-0 \\ z-1} = \pmatrix{0 \\ 2 \\ z-1}$

$\overrightarrow{CS_z}= \pmatrix{2-2 \\ 2-4 \\ z-1} = \pmatrix{0 \\ -2 \\ z-1}$

2. Schritt: Skalarprodukt berechnen

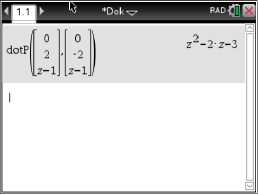Mathematische Darstellung in einer Software mit Matrizen und einer Gleichung.

Abb. 3: Skalarprodukt berechnen

3. Schritt: Gleichung lösen

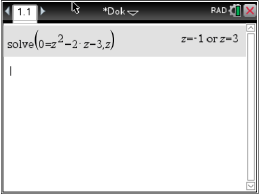Mathematische Gleichungslösung auf einem Bildschirm.

Abb. 4: Gleichung lösem

Du hast zwei Werte für $z$ gefunden, für welche die Gleichung erfüllt ist. Somit hast du gezeigt, dass es Punkte $S_z$ gibt, sodass das jeweilige Dreieck $ACS_z$ einen rechten Winkel beim Punkt $S_z$ hat.

$\blacktriangleright$ Prüfen, ob es einen Punkt in der Ebene $\boldsymbol{E}$ gibt, der drei gleiche Koordinaten hat

Um dies zu prüfen, stellst du als erstes die Ebenengleichung in Parameterform der Ebene $E$ auf und berechnest mit dieser die Koordinatengleichung der Ebene $E$ .

Setze dann einen Punkt mit drei gleichen Koordinaten, zum Beispiel $(x \;|\; x \;|\; x\;)$ , in die Koordinatengleichung ein. Ist die Gleichung lösbar, liegt ein Punkt mit drei gleichen Koordinaten in der Ebene $E$ .

1. Schritt: Ebenengleichung in Paramterform aufstellen

Bestimme mit den Punkten $B$ , $C$ und $S$ eine Ebenengleichung.

$\begin{array}[t]{rll} E: \overrightarrow{x}&=&... \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Ebenegleichung in Koordinatenform

Mit Hilfe des Vektorprodukts kannst du einen Normalenvektor der Ebene $E$ berechnen.

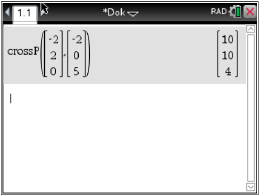Mathematische Berechnung mit Vektoren in einer Softwareanwendung.

Abb. 5: Normalenvektor berechnen

Diesen Vektor kannst du noch mit 2 kürzen.

$\overrightarrow{n}_E =\pmatrix{5 \\ 5 \\ -2}$

Die Normalengleichung der Ebene $E$ ist dann:

$E: 5x_1 + 5x_2 -2x_3 = d$

Setze die Koordinaten des Punktes $B$ ein, um $d$ zu berechnen.

$5\cdot 4 + 5\cdot 2 - 2\cdot 1 = 28$

Eine Ebenengleichung in Koordinatenform ist: $E: 5x_1 + 5x_2 -2x_3 = 28$

3. Schritt: Punkt mit drei gleichen Koordinaten einsetzen

Setze den Punkt mit den Koordinaten $(x \;|\; x \;|\; x\;)$ in die Ebenengleichung ein und löse die Gleichung nach $x$ auf. $\begin{array}[t]{rll} 5x + 5x -2x&=& 28 \\[5pt] 8x&=& 28 &\quad \scriptsize \mid\; :8 \\[5pt] x&=& 3,5 \end{array}$

In der Ebene $E$ gibt es einen Punkt bei dem alle Koordinaten gleich sind. Dieser Punkt hat die Koordinaten $(3,5\;|\; 3,5 \;|\; 3,5\;)$ .

$\blacktriangleright$ Prüfen, ob jede beliebige Ebene einen Punkt hat, der drei gleiche Koordinaten hat

Hier kannst du ähnlich wie im Aufgabenteil zuvor vorgehen. Bestimme eine allgemeine Form einer Ebene in Koordinatenform und setze einen beliebigen Punkt mit drei gleichen Koordinaten in die Ebenengleichung ein.

$E: ax_1+ bx_2 + cx_3 =d$

Setze den Punkt $(x \;|\; x \;|\; x\;)$ in die Ebenengleichung ein und löse die Gleichung nach $x$ auf.

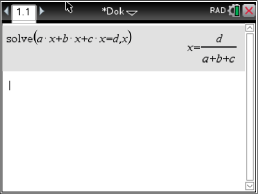Mathematik-Software zeigt eine Gleichung zur Lösung von x an.

Abb. 6: Gleichung lösen

In einer beliebigen Ebene gibt es einen Punkt, bei dem alle drei Koordinaten gleich sind, wenn gilt $a+b+c \neq 0$ . Somit liegt nicht in jeder Ebene ein Punkt, bei dem alle drei Koordinaten gleich sind.

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

[6]

$\blacktriangleright$ Zeigen, dass das Dreieck $\boldsymbol{ABC}$ gleischenklig ist

$\overrightarrow{AB} = \pmatrix{4-2 \\ 2-0 \\ 1-1} = \pmatrix{2 \\2 \\ 0}$

$\overrightarrow{BC} = \pmatrix{2-4 \\ 4-2 \\ 1-1} = \pmatrix{-2 \\2 \\ 0}$

$\overrightarrow{CA}=\pmatrix{2-2 \\ 0-4 \\ 1-1}= \pmatrix{0 \\-4 \\ 0}$

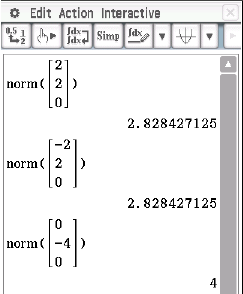Mathematische Berechnungen zur Norm von Vektoren mit Ergebnissen.

Abb. 1: Betrag der Vektoren

$\blacktriangleright$ Zeige, dass das Dreieck am Punkt $\boldsymbol{B}$ einen rechten Winkel hat

$\overrightarrow{AB} {\circ} \overrightarrow{BC}$

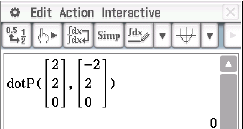Mathematische Darstellung eines Vektors mit einer Berechnung in einer Software.

Abb. 2: Skalarprodukt

Da das Skalarprodukt null ist, stehen die Vektoren $\overrightarrow{AB}$ und $\overrightarrow{BC}$ senkrecht aufeinander. Das Dreieck $ABC$ hat im Punkt $B$ einen rechten Winkel.

$\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{D}$ berechnen

In dieser Aufgabe sollst du die Koordinaten des Punktes $D$ berechnen, sodass die Punkte $A$ , $B$ , $C$ und $D$ die Eckpunkte eines Quadrates sind.

Um das Dreieck zu einem Quadrat zu ergänzen, kannst du den Vektor $\overrightarrow{BC}$ an den Ortsvektor, der zum Punkt $A$ zeigt addieren.

$\overrightarrow{OD}= \pmatrix{0 \\2 \\ 1}$

Vollständige Lösung anzeigen

Die Koordinaten des gesuchten Punktes $D$ kannst du jetzt ablesen.

Die Koordinaten des vierten Punktes sind $D(\;0 \;|\; 2 \;|\; 1 \;)$ .

$\blacktriangleright$ Winkel zwischen der Streck $\boldsymbol{\overline{AS}}$ und der Diagonalen $\boldsymbol{\overline{AC}}$ berechnen

Um den Winkel zwischen den beiden Strecken zu berechnen, bildest du als erstes die beiden Verbindungsvektoren $\overrightarrow{AS}$ und $\overrightarrow{AC}$ und berechnest den Winkel mit deinem Taschenrechner.

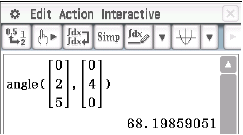Mathematische Berechnung des Winkels zwischen zwei Vektoren mit Resultat.

Abb. 3: Winkel berechnen

Der Winkel zwischen den Strecken $\overline{AS}$ und $\overline{AC}$ beträgt $68,12°$ .

$\blacktriangleright$ Zeigen, dass es Punkte $\boldsymbol{S_z}$ gibt, sodass das Dreieck $\boldsymbol{ACS_z}$ rechtwinklig ist

1. Schritt: Verbindungsvektoren berechnen

$\overrightarrow{AS_z}= \pmatrix{2-2 \\ 2-0 \\ z-1} = \pmatrix{0 \\ 2 \\ z-1}$

$\overrightarrow{CS_z}= \pmatrix{2-2 \\ 2-4 \\ z-1} = \pmatrix{0 \\ -2 \\ z-1}$

2. Schritt: Skalarprodukt berechnen

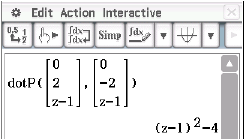Mathematische Darstellung mit einer Matrix und einer Berechnung.

Abb. 3: Skalarprodukt berechnen

3. Schritt: Gleichung lösen

Mathematische Software zeigt die Lösung einer Gleichung an.

Abb. 4: Gleichung lösem

$\blacktriangleright$ Prüfen, ob es einen Punkt in der Ebene $\boldsymbol{E}$ gibt, der drei gleiche Koordinaten hat

Um dies zu prüfen, stellst du als erstes die Ebenengleichung in Parameterform der Ebene $E$ auf und berechnest mit dieser die Koordinatengleichung der Ebene $E$ .

1. Schritt: Ebenengleichung in Paramterform aufstellen

Bestimme mit den Punkten $B$ , $C$ und $S$ eine Ebenengleichung.

$\begin{array}[t]{rll} E: \overrightarrow{x}&=&... \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Ebenegleichung in Koordinatenform

Mit Hilfe des Vektorprodukts kannst du einen Normalenvektor der Ebene $E$ berechnen.

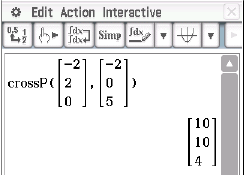Mathematische Berechnung mit Vektoren und Kreuzprodukt in einer Softwareanwendung.

Abb. 5: Normalenvektor berechnen

Diesen Vektor kannst du noch mit 2 kürzen.

$\overrightarrow{n}_E =\pmatrix{5 \\ 5 \\ -2}$

Die Normalengleichung der Ebene $E$ ist dann:

$E: 5x_1 + 5x_2 -2x_3 = d$

Setze die Koordinaten des Punktes $B$ ein, um $d$ zu berechnen.

$5\cdot 4 + 5\cdot 2 - 2\cdot 1 = 28$

Eine Ebenengleichung in Koordinatenform ist: $E: 5x_1 + 5x_2 -2x_3 = 28$

3. Schritt: Punkt mit drei gleichen Koordinaten einsetzen

Setze den Punkt mit den Koordinaten $(x \;|\; x \;|\; x\;)$ in die Ebenengleichung ein und löse die Gleichung nach $x$ auf.

$\begin{array}[t]{rll} 5x + 5x -2x&=& 28 \\[5pt] 8x&=& 28 &\quad \scriptsize \mid\; :8 \\[5pt] x&=& 3,5 \end{array}$

In der Ebene $E$ gibt es einen Punkt bei dem alle Koordinaten gleich sind. Dieser Punkt hat die Koordinaten $(3,5\;|\; 3,5 \;|\; 3,5\;)$ .

$\blacktriangleright$ Prüfen, ob jede beliebige Ebene einen Punkt hat, der drei gleiche Koordinaten hat

$E: ax_1+ bx_2 + cx_3 =d$

Setze den Punkt $(x \;|\; x \;|\; x\;)$ in die Ebenengleichung ein und löse die Gleichung nach $x$ auf.

Formel zur Lösung einer mathematischen Gleichung in einem Programm.

Abb. 6: Gleichung lösen

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

[6]