Aufgabe 3A
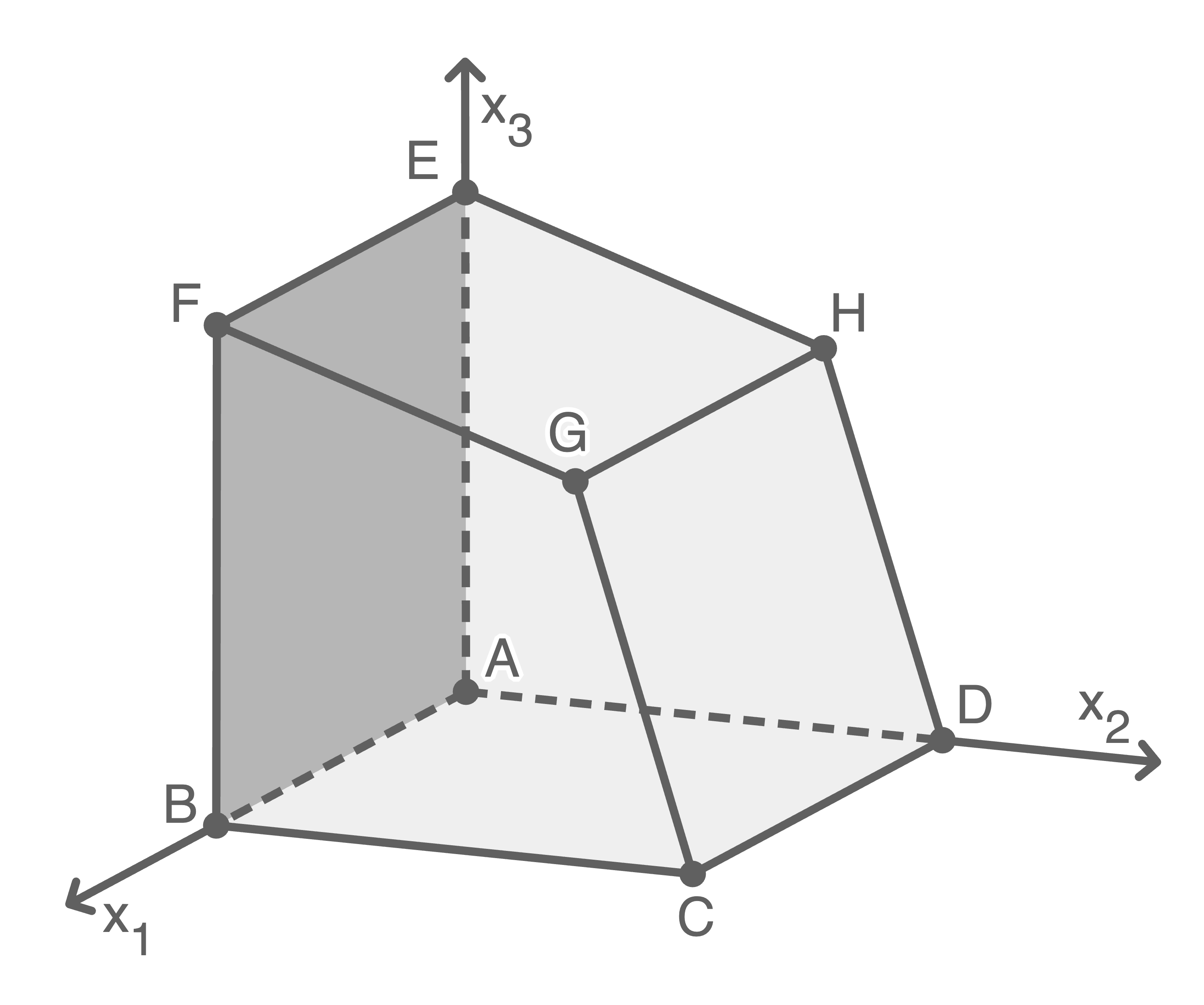
Ein Anbau eines Gebäudes wird durch das abgebildete Prisma mit den Eckpunkten 
und 
beschrieben.
Das Viereck 
stellt das Glasdach dar, das Viereck 
eine geschlossene Wand.
Die anderen Seiten des Anbaus bestehen vollständig aus Glas. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität. Die
-Ebene beschreibt den Untergrund, auf dem der Anbau steht.
und beschrieben.
Das Viereck stellt das Glasdach dar, das Viereck eine geschlossene Wand.
Die anderen Seiten des Anbaus bestehen vollständig aus Glas. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität. Die
-Ebene beschreibt den Untergrund, auf dem der Anbau steht.
a)
Begründe, dass das Viereck 
ein Drachenviereck ist.
ein Drachenviereck ist.
(3 BE)
b)
Bestimme die Größe des Winkels, den die Kanten 
und 
einschließen.
Die Punkte und einschließen.
(3 BE)
und 
liegen in der Ebene 
c)
Zeige, dass 
ein Spannvektor von 
ist.
ein Spannvektor von ist.
(3 BE)
d)
Begründe, dass das Viereck 
das Prisma 
in zwei zueinander symmetrische Teilkörper teilt.
Auf dem Glasdach kann ein Rollo herabgelassen werden.
das Prisma in zwei zueinander symmetrische Teilkörper teilt.
(3 BE)
Dabei bewegt sich das Rollo innerhalb einer Minute von der oberen Kante des Dachs, die durch
dargestellt wird, bis zur unteren Kante des Dachs.
e)
Bestimme die mittlere Geschwindigkeit, mit der das Rollo herabgelassen wird, in Zentimeter pro Sekunde.
Zu einem bestimmten Zeitpunkt kann das auf den Anbau treffende Sonnenlicht durch parallele Geraden mit dem Richtungsvektor
(3 BE)
beschrieben werden.
f)
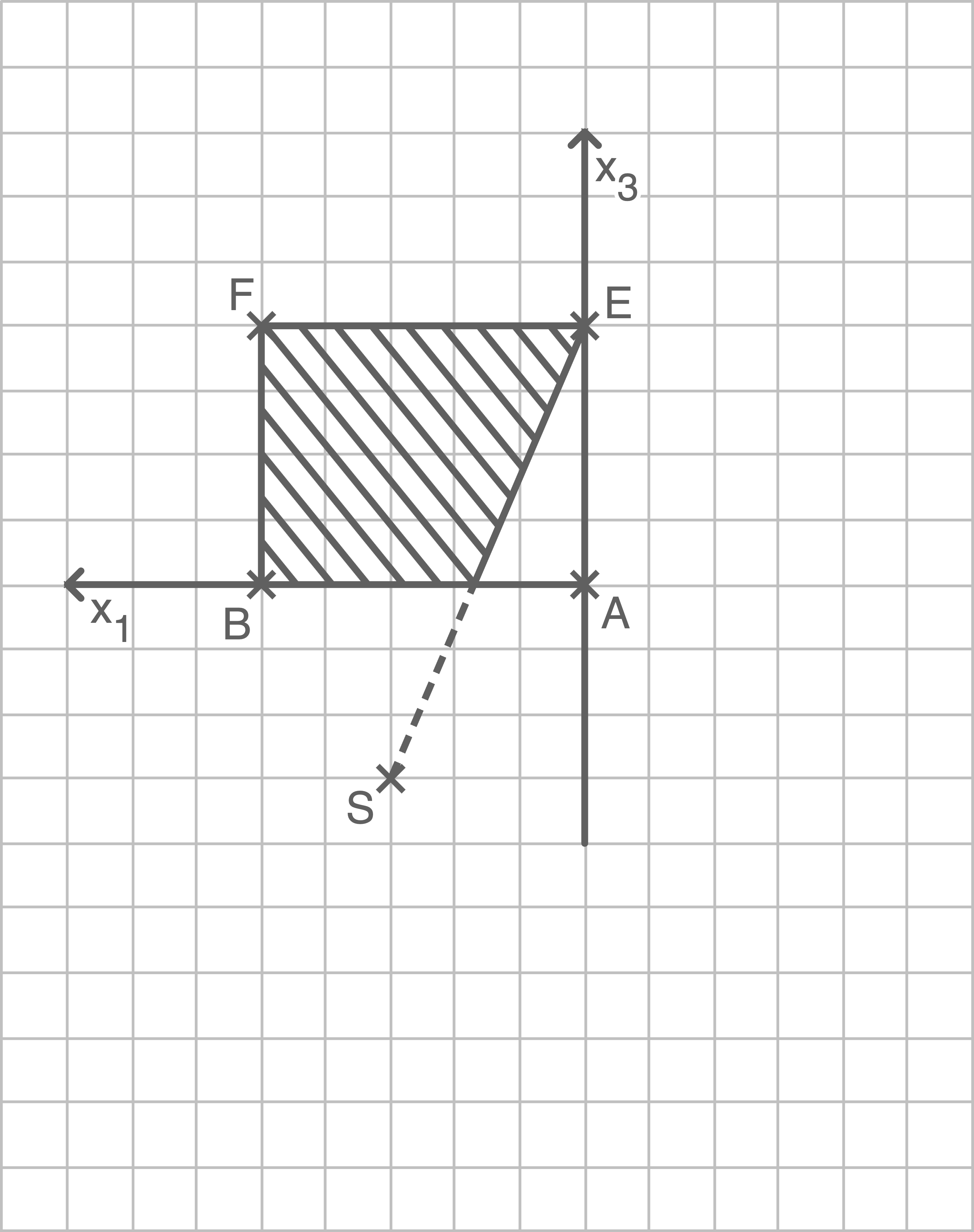
Das vollständig herabgelassene Rollo erzeugt auf der geschlossenen Wand einen Schatten. Dieser soll in der 
-Ebene grafisch dargestellt werden.
Die folgende Rechnung stellt einen wesentlichen Schritt zur Lösung dieser Aufgabe dar:
liefert 
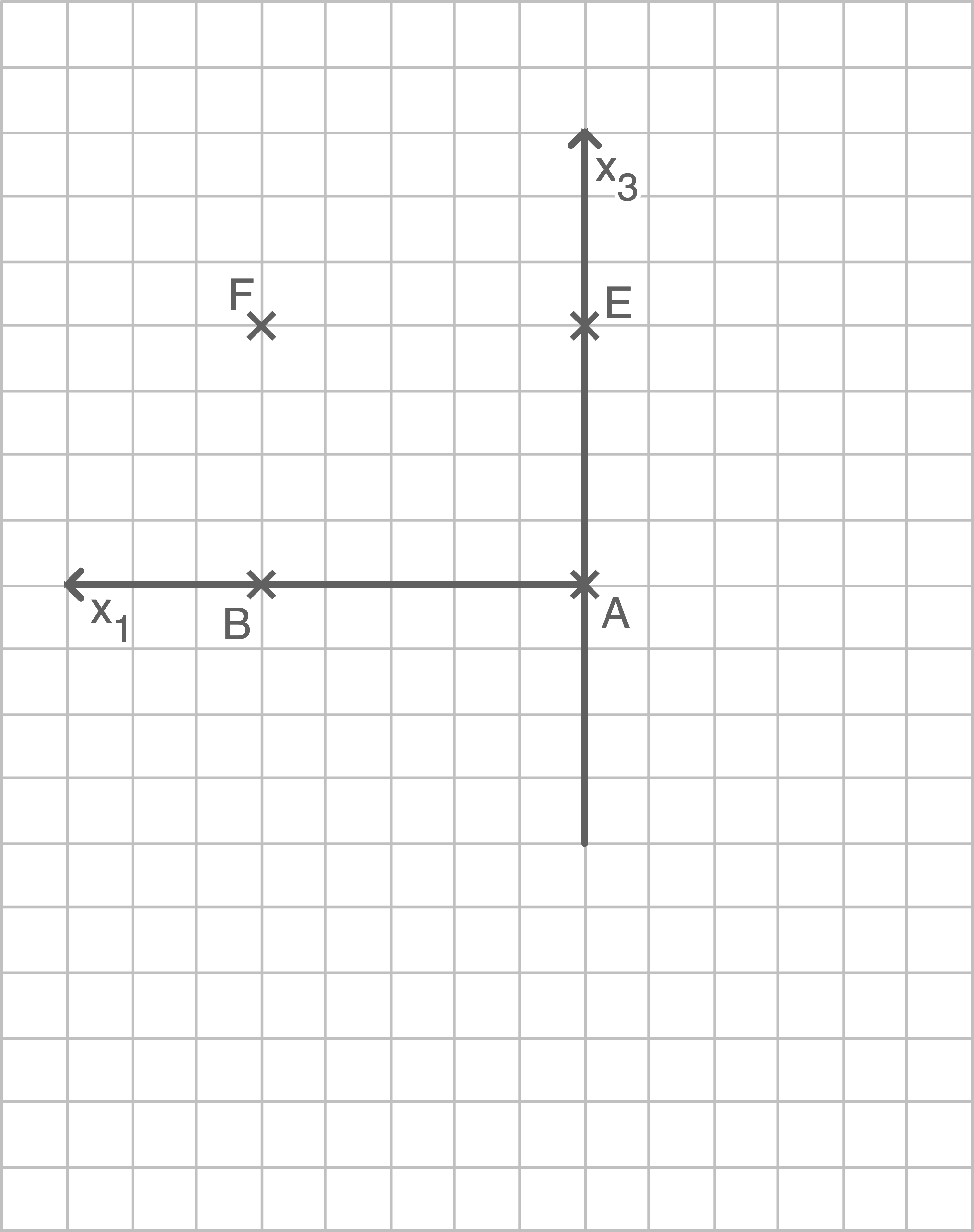
und damit 
Beschreibe die Bedeutung dieses Lösungsschritts und zeichne den Schatten in die folgende Abbildung ein.
-Ebene grafisch dargestellt werden.
Die folgende Rechnung stellt einen wesentlichen Schritt zur Lösung dieser Aufgabe dar:
liefert und damit
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
und 
gilt, ist das Viereck 
ein Drachenviereck.
b)
Es gilt:
![\(\begin{array}[t]{rll}
\cos (\alpha)&=& \dfrac{\overrightarrow{GF} \circ \overrightarrow{G C}}{|\overrightarrow{G F}| \cdot|\overrightarrow{G C}|} \\[5pt]
\cos (\alpha)&=& \dfrac{\pmatrix{0\\-3\\1} \circ \pmatrix{0\\1\\-3} }{\sqrt{10}\cdot \sqrt{10}} \\[5pt]
\cos (\alpha)&=& \dfrac{-3\cdot 1+1\cdot (-3)}{10} &\quad \scriptsize \mid\; \cos^{-1}\\[5pt]
\alpha &\approx& 127^\circ \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6c0d33fc247403c870e9f0217659e76bed697379a4f4f864127c788380bd9a4a_light.svg)
c)
Da die beiden Punkte 
und 
in der Ebene liegen, ist der Vektor 
ein Spannvektor von
Es gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{G H}&=& \pmatrix{0-5\\3-3\\3-3} & \\[5pt]
&=& \pmatrix{-5\\0\\0} & \\[5pt]
&=& -1\cdot \overrightarrow{AB}
\end{array}\)](https://www.schullv.de/resources/formulas/aad8aba847c80c3be9534ebfa919a5eaa640dbfa2c7d3f60093994032deabfda_light.svg)
Somit ist der Vektor kollinear zu 
und damit ebenfalls ein Spannvektor von
und in der Ebene liegen, ist der Vektor ein Spannvektor von
Es gilt:
Somit ist der Vektor kollinear zu und damit ebenfalls ein Spannvektor von
d)
Das Prisma mit dem Drachenviereck als Grundfläche ist gerade. Die Symmetrieachse der Grundfläche ist 
. Das Viereck steht senkrecht zur Grundfläche.
mit dem Drachenviereck als Grundfläche ist gerade. Die Symmetrieachse der Grundfläche ist . Das Viereck steht senkrecht zur Grundfläche.
e)
Für die Länge des Dachs gilt:
Da das Rollo diese Strecke innerhalb einer Minute zurücklegt, folgt für die mittlere Geschwindigkeit:
Da das Rollo diese Strecke innerhalb einer Minute zurücklegt, folgt für die mittlere Geschwindigkeit:
f)
Bedeutung beschreiben
ist der gemeinsame Punkt 
der Gerade durch 
mit dem gegebenen Richtungsvektor und der -Ebene.
Schatten zeichnen
ist der gemeinsame Punkt der Gerade durch mit dem gegebenen Richtungsvektor und der -Ebene.
Schatten zeichnen