Aufgabe Q1
Gegeben ist die in 
definierte ganzrationale Funktion 
mit 
Bestimme die Stammfunktion 
von 
deren Graph durch den Punkt 
verläuft.
Begründe ohne zu rechnen, dass 
ist.
Aufgabe Q2
Bei einem Onlinespiel wird einem Spieler zu Beginn des Spiels entweder Startpunkt 
oder Startpunkt 
zufällig zugewiesen. Die Wahrscheinlichkeit dafür, dass dem Spieler Startpunkt zugewiesen wird, beträgt 
Beginnt der Spieler das Spiel bei Startpunkt 
so beträgt die Wahrscheinlichkeit dafür, dass er im Spiel auf einen bestimmten Charakter trifft, 
Die Wahrscheinlichkeit dafür, dass dem Spieler Startpunkt zugewiesen wird und er auf diesen Charakter trifft, beträgt 
Erstelle zum beschriebenen Sachverhalt ein beschriftetes Baumdiagramm.
Ein Spieler beginnt das Spiel.
Gib im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem folgenden Term berechnet werden kann: 
Aufgabe Q3
Betrachtet werden die Punkte 
und 
Begründe, dass die Punkte 
und 
auf derselben Seite bezüglich der 
-Ebene liegen.
Die Punkte 
und der Koordinatenursprung 
sind die Eckpunkte eines gleichschenkligen Dreiecks, dessen Basis 
die Länge 
hat.
Ermittle den Flächeninhalt des Dreiecks.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Aufgabe Q1
Stammfunktion von 
aufstellen
berechnen
![\(\begin{array}[t]{rlll}
F(1) &=& 0 \\[5pt]
1^4-3 \cdot 1^2 +c &=& 0 \mid\; +2 \\[5pt]
c &=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/130ed1c95f062c0524bd614c20257a4122bb85618c5b25902e25060b9120f0e6_light.svg)
Die Stammfunktion, deren Graph durch den Punkt verläuft, ist:
Das Intervall ![\([-3 ; 3]\)](https://www.schullv.de/resources/formulas/44822fa36844621ad18d528fb4154ee3a1ec77f1a3101928dea102a70ecc03dd_light.svg)
ist symmetrisch zu 
und der Graph von ist punktsymmetrisch zum Koordinatenursprung, da der Term von nur Potenzen von 
mit ungeraden Exponenten enthält.
Aufgabe Q2
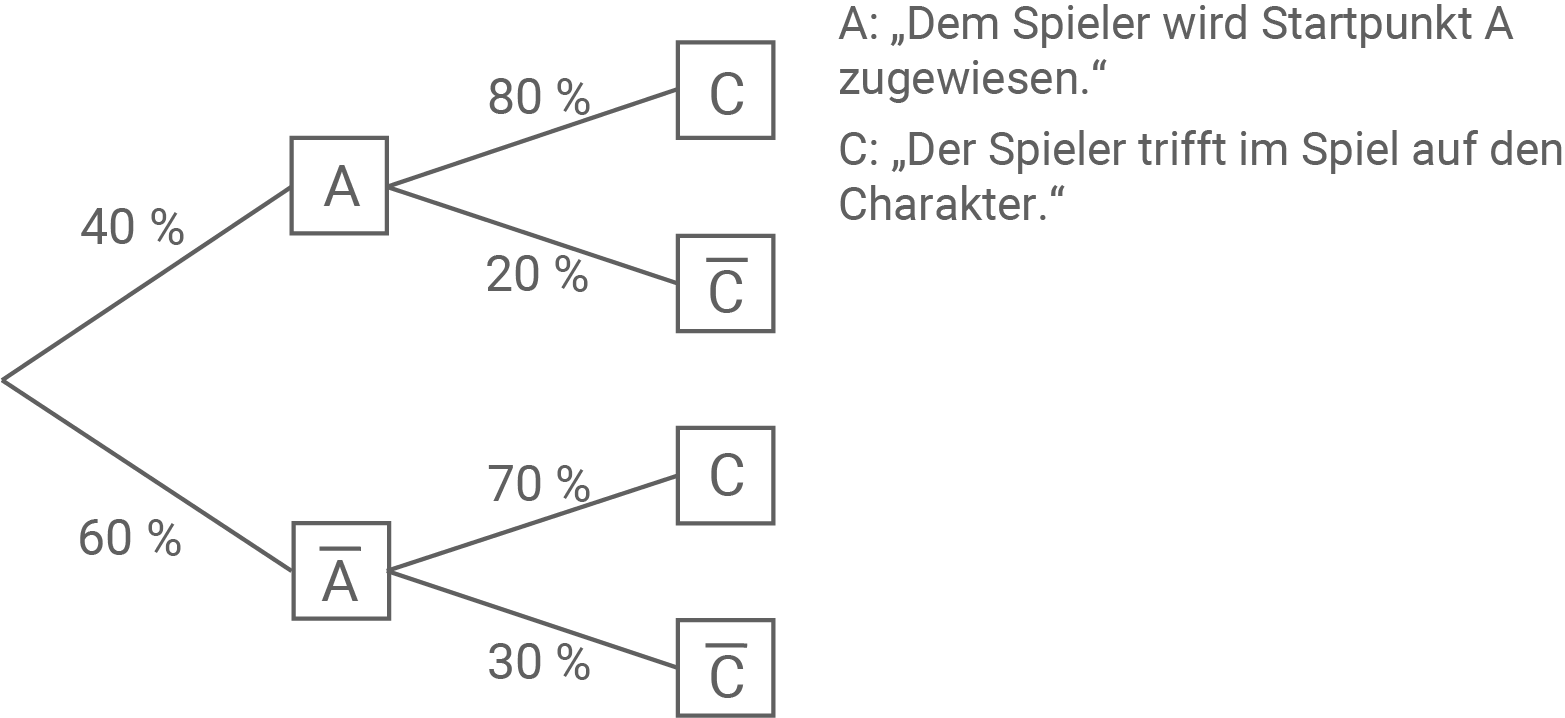
Der Teilterm 
bedeutet, dass der Spieler dem Startpunkt A zugewiesen wird und auf den Charakter trifft. Der Teilterm 
kann umgeschrieben werden in 
also, dass der Spieler nicht dem Startpunkt A zugewiesen wird aber auf den Charakter trifft. In der Klammer wird also die Wahrscheinlichkeit des Ereignisses 
berechnet.
Folglich beschreibt der Term 
die Wahrscheinlichtkeit des Gegenereignisses 
„Der Spieler trifft im Spiel nicht auf den Charakter.“
Aufgabe Q3
Die 
-Koordinaten beider Punkte haben das gleiche Vorzeichen.
Somit liegen die Punkte und auf derselben Seite bezüglich der -Ebene.
Mittelpunkt der Basis 
berechnen
![\(\begin{array}[t]{rlll}
\overrightarrow{OM} &=& \dfrac{1}{2} \cdot (\overrightarrow{O} + \overrightarrow{OQ}) \\[5pt]
&=&\dfrac{1}{2} \cdot\left(\pmatrix{0\\0\\0} + \pmatrix{4\\2\\-4}\right) \\[5pt]
&=& \pmatrix{2\\1\\-2}
\end{array}\)](https://www.schullv.de/resources/formulas/3ea9901da9acd9a1804a996a09a6ae42e1c00643ce354e98441e4d4742f4afac_light.svg)
Verbindungsvektor vom Mittelpunkt 
zum Punkt 
bestimmen
![\(\begin{array}[t]{rlll}
\overrightarrow{M P} &=& \overrightarrow{OP}-\overrightarrow{OM} \\[5pt]
&=& \pmatrix{3\\1\\-1} - \pmatrix{2\\1\\-2} \\[5pt]
&=& \pmatrix{1\\0\\1}
\end{array}\)](https://www.schullv.de/resources/formulas/c1b09b4bd51b66e5ded1fb44ae41bc7124cee6d2414d806c64b5fabae20616e6_light.svg)
Länge von 
berechnen
Flächeninhalt berechnen
![\(\begin{array}[t]{rlll}
A &=& \dfrac{1}{2} \cdot\left| \overline{OQ} \right| \cdot\left| \overline{MP} \right| \\[5pt]
&=&\dfrac{1}{2} \cdot 6 \cdot \sqrt{2} \\[5pt]
&=& 3\sqrt{2}
\end{array}\)](https://www.schullv.de/resources/formulas/7006969367d0e72f9061c472d606445bf4bdb33f7a0ee95f220fa1b6689a7de3_light.svg)