Aufgabe 3A

Ein Betrieb stellt Fruchtgummi aus der Grundsubstanz $\text{R1}$ und zwei Fruchtsaftkonzentraten $\text{R2}$ und $\text{R3}$ her. Es entstehen drei Sorten einzelner Fruchtgummitiere $\text{Z1}$ , $\text{Z2}$ und $\text{Z3}$ . Unterschiedliche Zusammensetzungen aus den drei Sorten ergeben die in Tüten verpackten Sortimente $\text{E1}$ und $\text{E2}$ . Die folgenden Tabellen geben an, wie viele Mengeneinheiten (ME) der Grundsubstanz und der Fruchtsaftkonzentrate für je ein Fruchtgummitier bzw. wie viel Stück der Fruchtgummitiere für je eine Tüte der jeweiligen Sortimente benötigt werden. Der dargestellte Übergangsgraph verdeutlicht den Produktionsprozess.

	Z1	Z2	Z3
R1	13	12	12
R2	3	2	2
R3	0	1	3

Tabelle $1$

	E1	E2
Z1	a	16
Z2	20	b
Z3	15	17

Tabelle $2$

Grafische Darstellung eines Netzwerkes mit Knoten und gerichteten Kanten.

Abb. 1: Produktionsprozess

Gib die fehlenden Werte für $a$ und $b$ aus Tabelle $2$ an.
Erläutere die Bedeutung des Eintrags $0$ in Tabelle $1$ im Sachzusammenhang.
Berechne den Bedarf für die Grundsubstanz $\text{R1}$ und die Fruchtsaftkonzentrate $\text{R2}$ und $\text{R3}$ für eine Produktion von $15$ Sortimenten $\text{E1}$ und $12$ Sortimenten $\text{E2}$ .

Es sollen $50$ Tüten des Sortiments $\text{E1}$ und $50$ Tüten des Sortiments $\text{E2}$ produziert werden. Im Lager befinden sich noch $2.000$ ME der Grundsubstanz $\text{R1}$ , $3.000$ ME des Fruchtsaftkonzentrats $\text{R2}$ und $1.000$ Stück der Fruchtgummitiere $\text{Z1}$ . Es sollen alle vorhandenen Materialien verwendet werden.
Bestimme die ME der Grundsubstanz und die ME aller Fruchtsaftkonzentrate, die für diese Produktion nachbestellt werden müssen.

(12P)

Eine Tüte eines neuen Sortiments $\text{E3}$ soll unter folgenden Bedingungen zusammengestellt werden:

Sie enthält insgesamt $50$ Stück der Fruchtgummitiere $\text{Z1}$ , $\text{Z2}$ und $\text{Z3}$ ,

von jeder Sorte der Fruchtgummitiere ist mindestens ein Stück enthalten,

es werden genau $140$ ME des Fruchtsaftkonzentrats $\text{R3}$ verwendet,

von der Grundsubstanz $\text{R1}$ und dem Fruchtsaftkonzentrat $\text{R2}$ stehen beliebig viele ME zur Verfügung.

Untersuche, aus welchen Stückzahlen der Fruchtgummitiere die Tüte des neuen Sortiments $\text{E3}$ zusammengestellt werden kann.

(5P)

Bildnachweise [nach oben]

[1]

Aufgabe 3A

$\blacktriangleright$ Fehlende Werte für $\boldsymbol{a}$ und $\boldsymbol{b}$ angeben

Mit Hilfe des gegebenen Übergangsgraphen sollst du die fehlenden Werte für $a$ und $b$ in Tabelle 2 bestimmen. Diese Tabelle beschreibt, wie viele Fruchtgummitiere $Z1$ , $Z2$ und $Z3$ jeweils in den Tüten $E1$ und $E2$ drin sind. Der Wert $a$ ist die Anzahl der Fruchtgummitiere $Z1$ , die in der Tüte $E1$ enthalten sind. Aus dem Graphen abgelesen erhältst du:

$a=15$

Der Wert $b$ gibt an, wie viele Fruchtgummitiere $Z2$ in der Packung $E2$ sind. Auch diesen Wert kannst du aus dem Übergangsgraphen ablesen.

$b=17$

Der Wert für $a=15$ und für $b=17$ .

$\blacktriangleright$ Eintrag $\boldsymbol{0}$ erläutern

In der Tabelle 1 gibt es einen Eintrag 0. Dieser Eintrag bedeutet, dass für die Fruchtgummitiere $Z1$ $0$ Mengeneinheiten vom Fruchtsaftkonzentrat $R3$ benötigt werden.

$\blacktriangleright$ $\boldsymbol{ME}$ von $\boldsymbol{R1}$ , $\boldsymbol{R2}$ und $\boldsymbol{R3}$ berechnen

In dieser Aufgabe sollst du berechnen, wie viele Mengeneinheiten der Grundsubstanz $R1$ und der Fruchtsaftkonzentrate $R2$ und $R3$ benötigt werden, um $15$ Tüten $E1$ und $12$ Tüten $E2$ produzieren zu können.

Dazu kannst du die Übergangsmatrix $M_1$ (Tabelle 2) mit einem Verteilungsvektor $\overrightarrow{v}$ multiplizieren. Da $15$ Tüten von $E1$ und $12$ Tüten $E2$ hergestellt werden, hat der Vektor die Einträge $\overrightarrow{v}=\pmatrix{15 \\ 12}$ . Du erhältst als Ergebnis einen Vektor $\overrightarrow{w}$ , den du dann mit der Übergangsmatrix $M_2$ (Tabelle 1) multiplizierst. Du erhälrst wieder einen Vektor, der nun angibt wie viele Mengeneinheiten $R1$ , $R2$ und $R3$ benötigt werden.

1. Schritt: $\boldsymbol{M_1}$ mit $\boldsymbol{\overrightarrow{v}}$ multiplizieren

$M_1 \cdot \overrightarrow{v}= \pmatrix{417 \\ 504 \\ 429} =\overrightarrow{w}$

Vollständige Lösung anzeigen

2. Schritt: $\boldsymbol{M_2}$ mit $\boldsymbol{\overrightarrow{w}}$ multiplizieren

$M_2 \cdot \overrightarrow{w} = \pmatrix{16.617 \\ 3.117 \\ 1.791}$

Vollständige Lösung anzeigen

Es werden $16.617\;ME$ der Grundsubstanz $R1$ benötigt und von den Fruchtsaftkonzentraten werden folgende Mengeneinheiten benötigt: $R2= 3.117$ und $R3=1.791$ .

$\blacktriangleright$ $\boldsymbol{ME}$ berechnen, die nachbestellt werden müssen

In dieser Aufgabe sollen jeweils $50$ Tüten $E1$ und $E2$ hergestellt werden. Im Lager befinden sich noch:

Grundsubstanz $R1$ :	$2.000\;ME$
Fruchtsaftkonzentrat $R2$ :	$3.000\;ME$
Fruchtgummitiere $Z1$	$1.000\;ME$

Berechne als erstes, wie viele Fruchtgummitiere hergestellt werden müssen. Multipliziere die Matrix $M_1$ des Übergangsgraphen (Tabelle 2) mit einem Verteilungsvektor $\overrightarrow{v}$ . Da $50$ Tüten von $E1$ und $E2$ hergestellt werden sollen, hat der Verteilungsvektor die Einträge $\overrightarrow{v}=\pmatrix{50 \\ 50}$ . Als Ergebnis erhältst du einen Vektor $\overrightarrow{w}$ , der angibt, wie viele Fruchtgummitiere $Z1$ , $Z2$ und $Z3$ hergestellt werden müssen. Diesen kannst du anschließend mit der zweiten Übergangsmatrix $M_2$ (Tabelle 1) multiplizieren und du erhältst die Mengeneinheiten der benötigten Fruchtsaftkonzentrate. Um dann zu berechnen, wie viele Mengeneinheiten noch bestellt werden müssen, subtrahierst du die Vorräte mit den benötigten Mengeneinheiten.

1. Schritt: $\boldsymbol{M_1}$ mit $\boldsymbol{\overrightarrow{v}}$ multiplizieren

$M_1 \cdot \overrightarrow{v} = \pmatrix{1.550 \\ 1.850 \\ 1.600}$

Vollständige Lösung anzeigen

Von den Fruchtgummitieren $Z1$ sind noch $1.000$ vorrätig, es müssen also nur $550$ produziert werden. Somit ändert sich der erste Eintrag des Vektors $\overrightarrow{w} = \pmatrix{550 \\ 1.850 \\ 1.600}$ .

2. Schritt: $\boldsymbol{M_2}$ mit $\boldsymbol{\overrightarrow{w}}$ multiplizieren

$M_2 \cdot \overrightarrow{w} = \pmatrix{48.550 \\ 8.550 \\6.650 }$

Vollständige Lösung anzeigen

3. Schritt: Benötigte Mengen mit den Vorräten verrechnen

Von der Grundsubstanz $R1$ werden $48.550\; ME$ benötigt, $2.000\;ME$ sind vorrätig.

$R1= 48.550 - 2.000 = 46.550$

Vom Fruchtsaftkonzentrat $R2$ werden $11.550\;ME$ benötigt und $3.000\;$ sind vorrätig.

$R2= 8.550 - 3.000 = 5.550$

Von der Grundsubstanz $R1$ müssen $46.550\; ME$ bestellt werden und von den Fruchtsaftkonzentraten müssen folgende Mengeneinheiten bestellt werden: $R2=5.550$ und $R3=6.650$ .

$\blacktriangleright$ Stücksazhl der Fruchtgummitiere bestimmen

In dieser Aufgabe sollst du bestimmen, aus welcher Stückzahl der Fruchtgummitiere $Z1$ , $Z2$ und $Z3$ eine neue Tüte des Sortiments $E3$ zusammengestellt werden kann. Dabei hast du drei Bedingungen gegeben.

Die erste ist, dass insgesamt $50$ Fruchtgummitiere in einer Tüte sind. Die Gleichung $\text{I}:\;z_1+z_2+z_3 = 50$ muss erfüllt sein.

Die zweite Bedingung ist, dass von jeder Sorte $Z1$ , $Z2$ , $Z3$ mindestens ein Stück in der Tüte sein soll. Da aber höchstens $50$ Fruchtgummitiere in einer Tüte sein dürfen, bedeutet das
$\text{II}:\;1\leq z_i \leq 48$ , mit $i\in$ { $1,2,3$ }.

Die dritte Bedingung ist, dass genau $140\;ME$ des Fruchtsaftkonzentrats $R3$ verwendet werden. Damit erhältst du die Gleichung:
$\text{III}:\;z_2 + 2z_3 = 140$ .

Du erhältst ein überbestimmtes Gleichungssystem. Stelle die erste und dritte Gleichung nach $z_1$ und $z_2$ um. Den Wert für $z_3$ erhältst du dann, wenn du den Schnittpunkt zwischen den beiden Geraden $z_1$ und $z_2$ berechnest. Erfüllt der Wert für $z_3$ die zweite Bedingung, kannst du die Werte für $z_1$ und $z_2$ berechnen. Erfüllen auch diese Werte die zweite Bedingung, hast du die Stückzahl der Fruchgummitiere berechnet.

1. Schritt: Gleichungen umformen

$\begin{array}[t]{rll} & z_2 &=& 140- 3z_3 \end{array}$

Vollständige Lösung anzeigen

Setze $z_2$ in die erste Gleichung ein und löse diese nach $z_1$ auf.

$\begin{array}[t]{rll} & z_1 &=& 2z_3 -90 \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Schnittpunkt berechnen

Berechne den Schnittpunkt der beiden Gleichungen, in dem du sie Gleichsetzt und den solve-Befehl deines Taschenrechners verwendest.

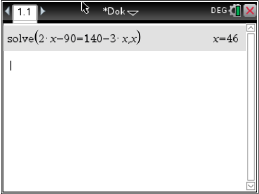Mathematische Gleichungslösung auf einem Bildschirm dargestellt.

Abb. 1: Schnittpunkt berechnen

$x=z_3 = 46$

Da $1 \leq 46\leq 48$ ist auch die zweite Bedingung erfüllt.

3. Schritt: Werte für $\boldsymbol{z_2}$ und $\boldsymbol{z_3}$ berechnen

Setze $z_3=46$ in die Gleichungen $z_2$ und $z_3$ ein.

$z_1= -90+2\cdot 46 = 2$

$z_2 = 140-3\cdot 46 = 2$

Da auch diese beide Werte die zweite Bedingung erfüllen, ist die Tüte $E3$ aus $2$ Fruchtgummitieren $Z1$ , $2$ Fruchtgummitieren $Z2$ und $46$ Fruchtgummitieren $Z3$ zusammengesetzt.

Bildnachweise [nach oben]

[1]

Aufgabe 3A

$\blacktriangleright$ Fehlende Werte für $\boldsymbol{a}$ und $\boldsymbol{b}$ angeben

$a=15$

Der Wert $b$ gibt an, wie viele Fruchtgummitiere $Z2$ in der Packung $E2$ sind. Auch diesen Wert kannst du aus dem Übergangsgraphen ablesen.

$b=17$

Der Wert für $a=15$ und für $b=17$ .

$\blacktriangleright$ Eintrag $\boldsymbol{0}$ erläutern

In der Tabelle 1 gibt es einen Eintrag 0. Dieser Eintrag bedeutet, dass für die Fruchtgummitiere $Z1$ $0$ Mengeneinheiten vom Fruchtsaftkonzentrat $R3$ benötigt werden.

$\blacktriangleright$ $\boldsymbol{ME}$ von $\boldsymbol{R1}$ , $\boldsymbol{R2}$ und $\boldsymbol{R3}$ berechnen

1. Schritt: $\boldsymbol{M_1}$ mit $\boldsymbol{\overrightarrow{v}}$ multiplizieren

$M_1 \cdot \overrightarrow{v}= \pmatrix{417 \\ 504 \\ 429} =\overrightarrow{w}$

Vollständige Lösung anzeigen

2. Schritt: $\boldsymbol{M_2}$ mit $\boldsymbol{\overrightarrow{w}}$ multiplizieren

$M_2 \cdot \overrightarrow{w} = \pmatrix{16.617 \\ 3.117 \\ 1.791}$

Vollständige Lösung anzeigen

Es werden $16.617\;ME$ der Grundsubstanz $R1$ benötigt und von den Fruchtsaftkonzentraten werden folgende Mengeneinheiten benötigt: $R2= 3.117$ und $R3=1.791$ .

$\blacktriangleright$ $\boldsymbol{ME}$ berechnen, die nachbestellt werden müssen

In dieser Aufgabe sollen jeweils $50$ Tüten $E1$ und $E2$ hergestellt werden. Im Lager befinden sich noch:

Grundsubstanz $R1$ :	$2.000\;ME$
Fruchtsaftkonzentrat $R2$ :	$3.000\;ME$
Fruchtgummitiere $Z1$	$1.000\;ME$

1. Schritt: $\boldsymbol{M_1}$ mit $\boldsymbol{\overrightarrow{v}}$ multiplizieren

$M_1 \cdot \overrightarrow{v} = \pmatrix{1.550 \\ 1.850 \\ 1.600}$

Vollständige Lösung anzeigen

2. Schritt: $\boldsymbol{M_2}$ mit $\boldsymbol{\overrightarrow{w}}$ multiplizieren

$M_2 \cdot \overrightarrow{w} = \pmatrix{48.550 \\ 8.550 \\6.650 }$

Vollständige Lösung anzeigen

3. Schritt: Benötigte Mengen mit den Vorräten verrechnen

Von der Grundsubstanz $R1$ werden $48.550\; ME$ benötigt, $2.000\;ME$ sind vorrätig.

$R1= 48.550 - 2.000 = 46.550$

Vom Fruchtsaftkonzentrat $R2$ werden $11.550\;ME$ benötigt und $3.000\;$ sind vorrätig.

$R2= 8.550 - 3.000 = 5.550$

Von der Grundsubstanz $R1$ müssen $46.550\; ME$ bestellt werden und von den Fruchtsaftkonzentraten müssen folgende Mengeneinheiten bestellt werden: $R2=5.550$ und $R3=6.650$ .

$\blacktriangleright$ Stücksazhl der Fruchtgummitiere bestimmen

Die erste ist, dass insgesamt $50$ Fruchtgummitiere in einer Tüte sind. Die Gleichung $\text{I}:\;z_1+z_2+z_3 = 50$ muss erfüllt sein.

Die zweite Bedingung ist, dass von jeder Sorte $Z1$ , $Z2$ , $Z3$ mindestens ein Stück in der Tüte sein soll. Da aber höchstens $50$ Fruchtgummitiere in einer Tüte sein dürfen, bedeutet das
$\text{II}:\;1\leq z_i \leq 48$ , mit $i\in$ { $1,2,3$ }.

Die dritte Bedingung ist, dass genau $140\;ME$ des Fruchtsaftkonzentrats $R3$ verwendet werden. Damit erhältst du die Gleichung:
$\text{III}:\;z_2 + 2z_3 = 140$ .

1. Schritt: Gleichungen umformen

$\begin{array}[t]{rll} & z_2 &=& 140- 3z_3 \end{array}$

Vollständige Lösung anzeigen

Setze $z_2$ in die erste Gleichung ein und löse diese nach $z_1$ auf.

$\begin{array}[t]{rll} & z_1 &=& 2z_3 -90 \end{array}$

Vollständige Lösung anzeigen

2. Schritt: Schnittpunkt berechnen

Berechne den Schnittpunkt der beiden Gleichungen, in dem du sie Gleichsetzt und den solve-Befehl deines Taschenrechners verwendest.

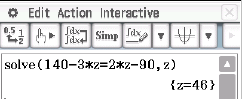Mathematische Gleichungslösung in einer Software, die das Ergebnis z = 46 anzeigt.

Abb. 1: Schnittpunkt berechnen

$x=z_3 = 46$

Da $1 \leq 46\leq 48$ ist auch die zweite Bedingung erfüllt.

3. Schritt: Werte für $\boldsymbol{z_2}$ und $\boldsymbol{z_3}$ berechnen

Setze $z_3=46$ in die Gleichungen $z_2$ und $z_3$ ein.

$z_1= -90+2\cdot 46 = 2$

$z_2 = 140-3\cdot 46 = 2$

Da auch diese beide Werte die zweite Bedingung erfüllen, ist die Tüte $E3$ aus $2$ Fruchtgummitieren $Z1$ , $2$ Fruchtgummitieren $Z2$ und $46$ Fruchtgummitieren $Z3$ zusammengesetzt.

Bildnachweise [nach oben]

[1]