Analytische Geometrie

Aufgabe 3A

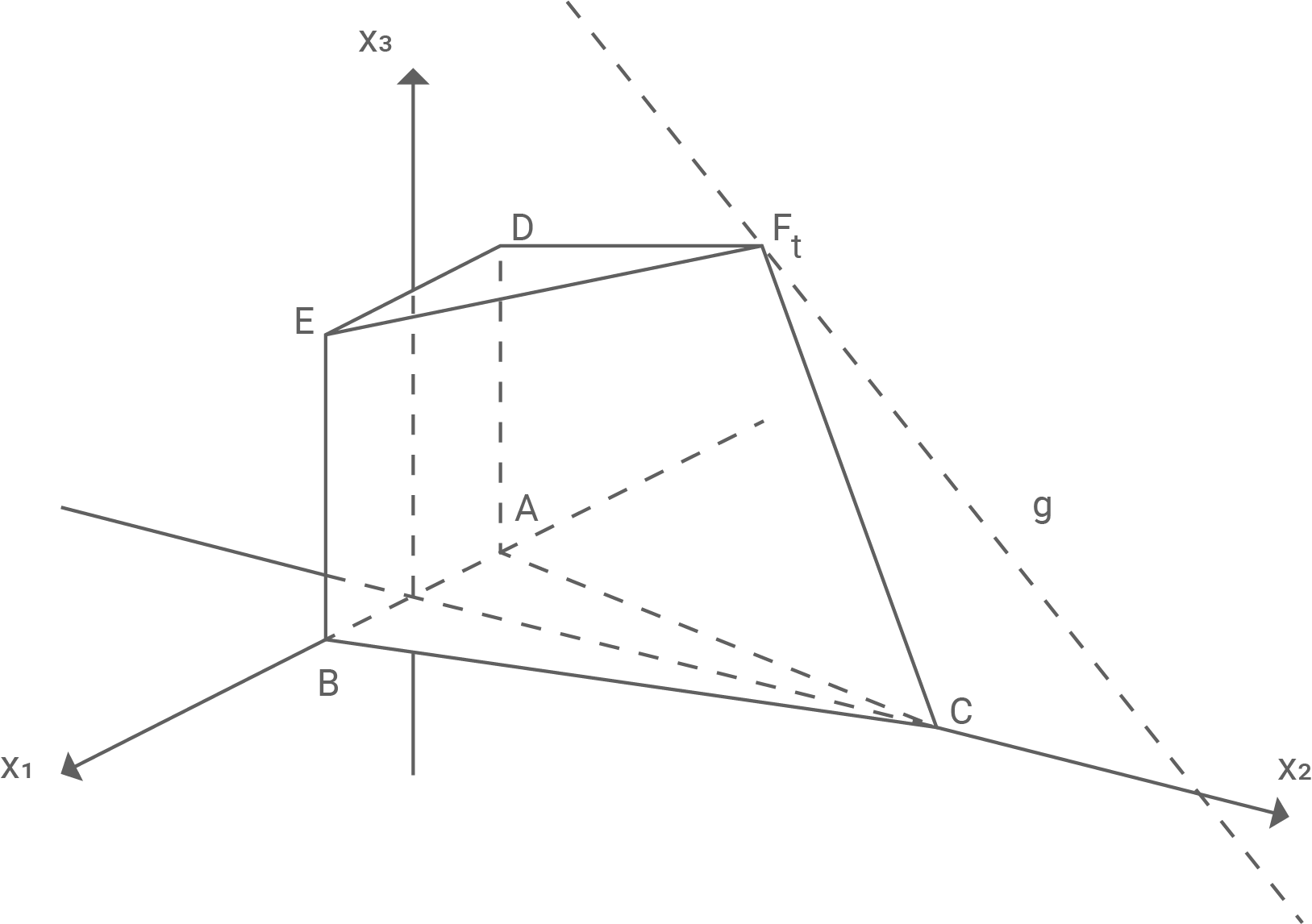
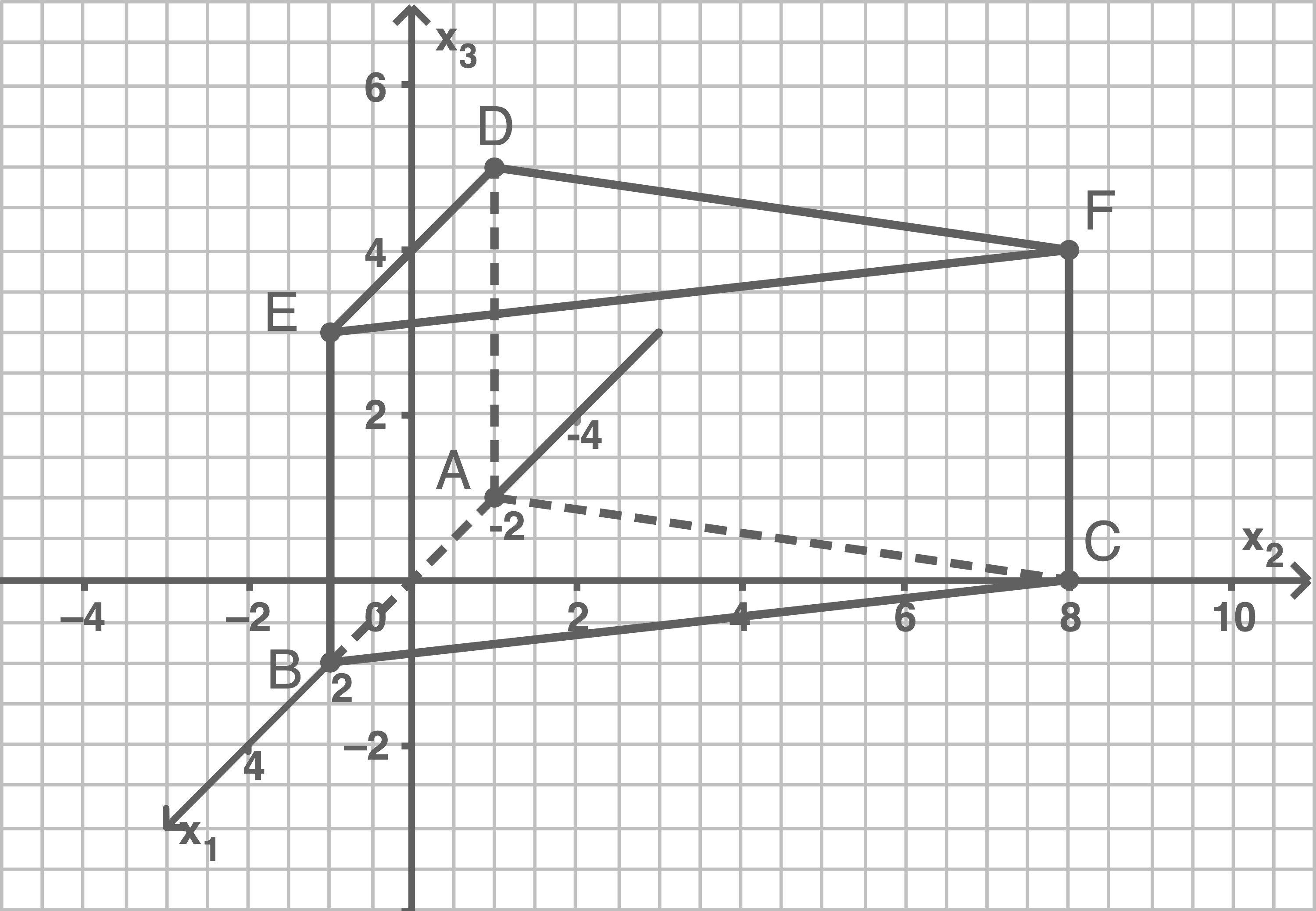
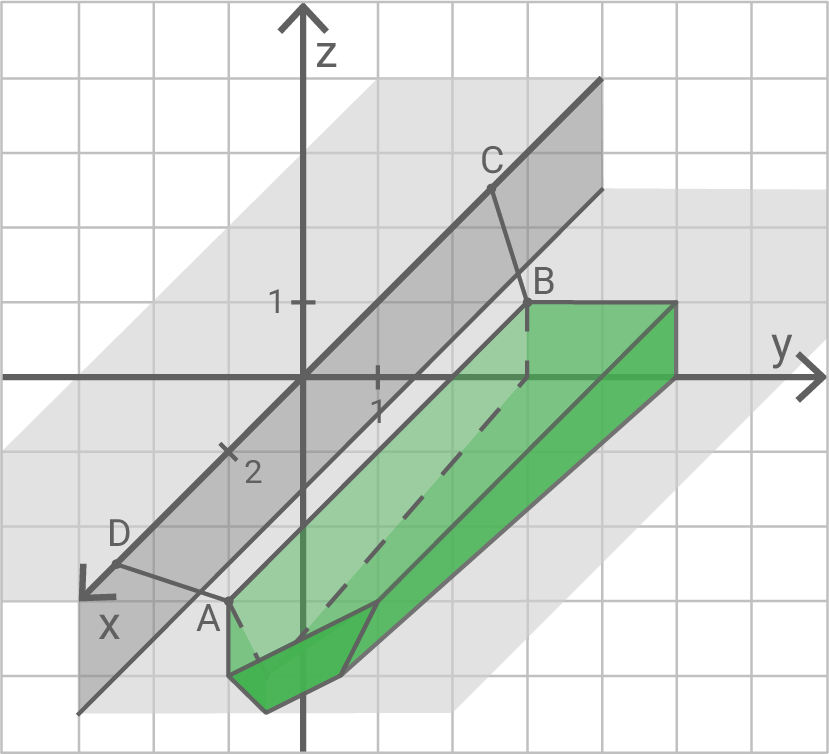
Betrachtet wird ein gerades Prisma mit den Eckpunkten
$A, B, C, D, E$ und $F.$ Seine Grundfläche ist das Dreieck $A B C.$
$A(-2 \mid 0 \mid 0), B(2 \mid 0 \mid 0), C(0 \mid 8 \mid 0),$
$D(-2 \mid 0 \mid 4), E(2 \mid 0 \mid 4)$ und $F(0 \mid 8 \mid 4).$

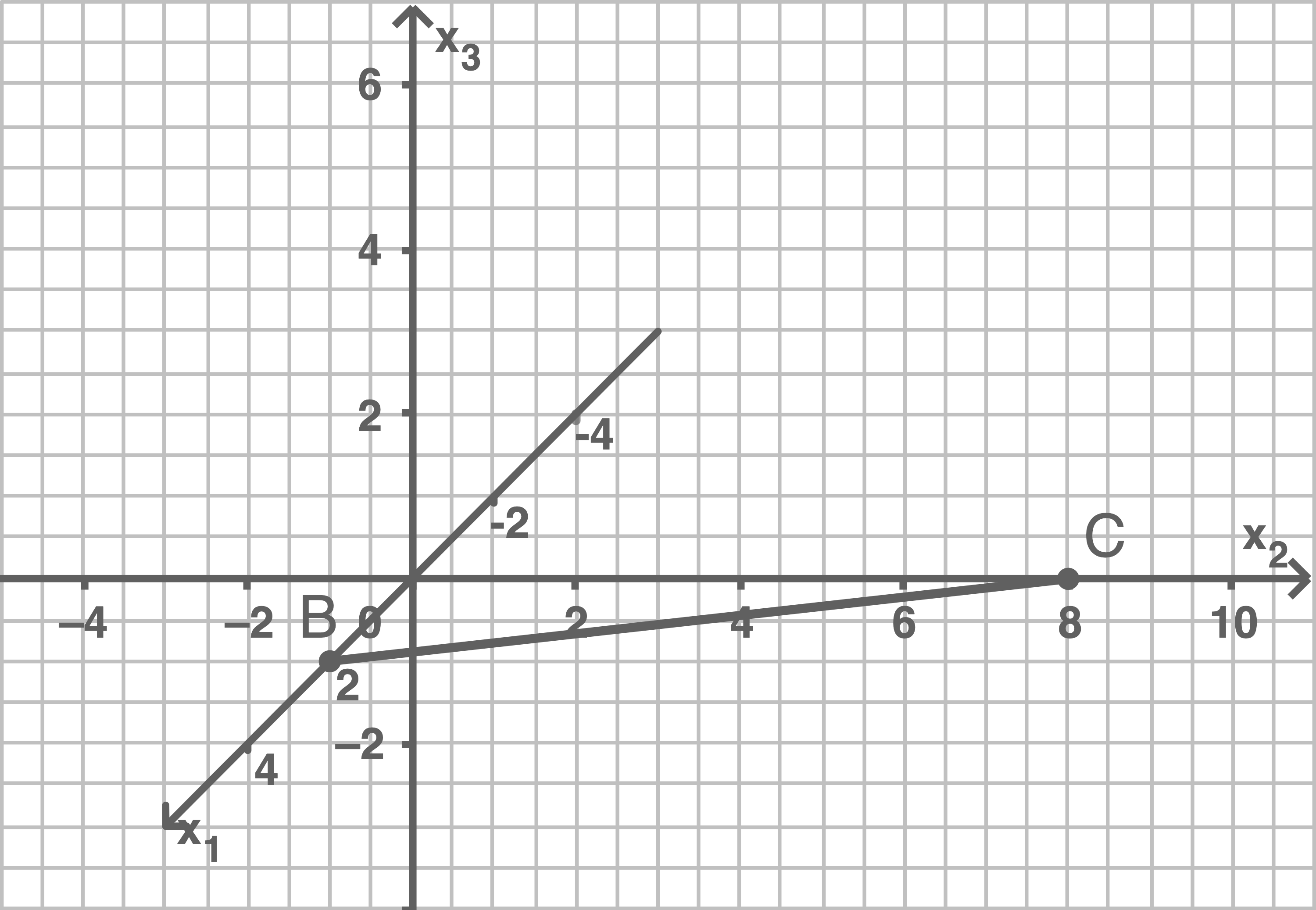
Abbildung

Abbildung 1

Abbildung 1 zeigt die Kante $\overline{B C}$ des Prismas.

Zeichne das Prisma in Abbildung 1 ein und berechne das Volumen des Prismas.

(5 BE)

Die Seitenfläche $B C F E$ liegt in der Ebene $H.$

Bestimme eine Gleichung von $H.$

Gib die Koordinaten eines weiteren Punktes auf der Seitenfläche $B C F E$ an.

$\left[\text{Zur Kontrolle: } H: \overrightarrow{x}=\pmatrix{2\\0\\0}+s \cdot \pmatrix{-2\\8\\0}+t \cdot \pmatrix{0\\0\\4} ; s, t \in \mathbb{R}\right]$

(3 BE)

Die Ebene $H$ liegt parallel zu einer der drei Koordinatenachsen.

Gib diese Achse an und begründe deine Angabe anhand der Gleichung dieser Ebene.

(2 BE)

Im Folgenden wird die Gerade $g$ mit der Gleichung $\overrightarrow{x}=\pmatrix{0\\0\\12}+t \cdot \pmatrix{0\\1\\-1},t \in \mathbb{R}$ betrachtet.
Des Weiteren wird der Punkt $F$ durch den Punkt $F_t(0 \mid t \mid 12-t)$ mit $0 \lt t \leq 8$ ersetzt. Für jeden Wert von $t$ liegt der Punkt $F_t$ auf der Gerade $g$ (vgl. Abbildung 2).
Mit $M$ wird der Mittelpunkt der Basis $\overline{D E}$ des gleichschenkligen Dreiecks $E F_t D$ bezeichnet.

Abbildung

Abbildung 2

Zeige rechnerisch, dass für $t=4$ die Strecke $\overline{M F_t}$ senkrecht auf der Gerade $g$ steht.

(2 BE)

Begründe ohne Rechnung, dass der Flächeninhalt des Dreiecks $E F_t D$ für $t=4$ am kleinsten ist.

(3 BE)

Aufgabe 3B

In manchen Häfen ändert sich die Höhe des Wasserstandes z. B. aufgrund von Gezeiten sehr stark. Dies muss beim Festmachen von Booten berücksichtigt werden. Es werden zwei von mehreren Leinen betrachtet, mit denen ein Boot festgemacht ist. Dabei wird Punkt $A(4\mid 1\mid a)$ mit Punkt $D(5\mid 0\mid 0)$ und Punkt $B(-4\mid 1\mid a)$ mit Punkt $C(-5\mid0\mid0)$ verbunden. Es gilt $-4 \leq a \leq-0,5.$ An einem bestimmten Tag stellt $a=-4$ die Situation bei Niedrigwasser und $a=-0,5$ bei Hochwasser dar. Abbildung 2 zeigt die Situation für $a=-1.$ Zur Vereinfachung wird davon ausgegangen, dass sich das Boot bei verändertem Wasserstand nur auf und ab bewegt. Alle Angaben sind in Meter $(\text{m}).$

Abbildung

Abbildung 1

Abbildung

Abbildung 2

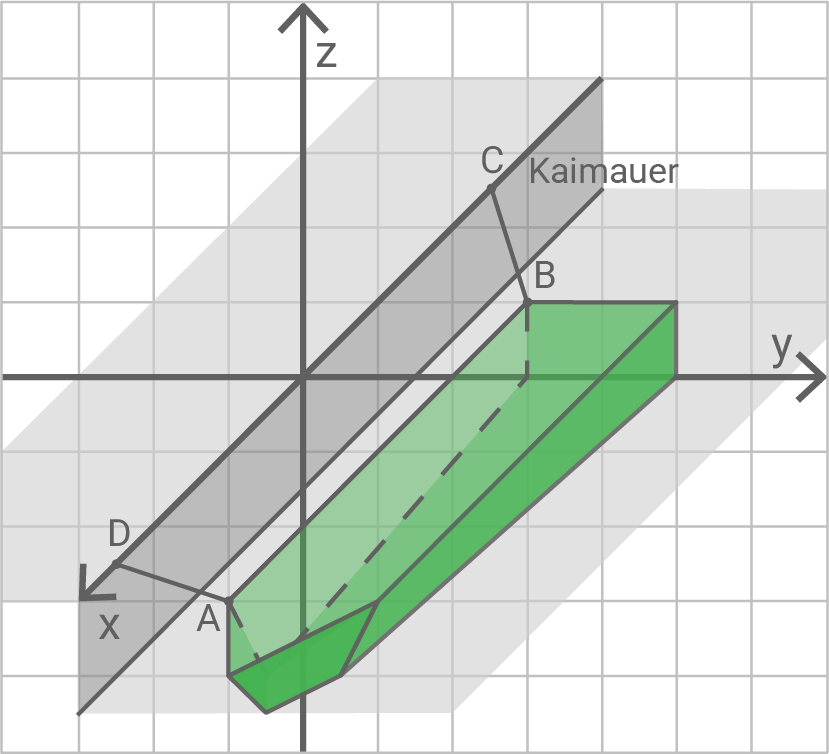
Ergänze die Skalierung des Koordinatensystems in Abbildung 2.

(2 BE)

Zeige, dass die Figur $A B C D$ ein symmetrisches Trapez ist.

(3 BE)

Zum Festmachen muss bei jeder Leine eine zusätzliche Länge von $1,5 \; \text{m}$ berücksichtigt werden.

Es wird die notwendige Länge der Leinen bei Niedrigwasser betrachtet.

Bestimme, welche Länge die Leine bei Befestigung in den Punkten $A$ und $D$ mindestens haben muss.

(3 BE)

Bestimme einen Wert von $a,$ sodass der Winkel zwischen der vorderen Leine und der Bootskante $\overline{A B}$ die Größe $110^{\circ}$ hat.

(3 BE)

Auf der Kaimauer befindet sich ein weiterer Befestigungspunkt $P(7\mid -0,5\mid 0,5).$ Das Boot wird zusätzlich in den Punkten $A$ und $P$ festgemacht.

Untersuche, ob die Leine zwischen $A$ und $P$ bei Niedrigwasser an der Kante der Kaimauer abknickt.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Aufgabe 3A

Abbildung

Volumen: $\dfrac{1}{2} \cdot 4 \cdot 8 \cdot 4=64$

Spannvektor $\boldsymbol{\overrightarrow{BC}}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{BC} &=& \overrightarrow{OC}-\overrightarrow{OB} \\[5pt] &=& \pmatrix{0\\8\\0} - \pmatrix{2\\0\\0} \end{array}$

Spannvektor $\boldsymbol{\overrightarrow{BE}}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{BE} &=& \overrightarrow{OE}-\overrightarrow{OB} \\[5pt] &=& \pmatrix{2\\0\\4} - \pmatrix{2\\0\\0} \end{array}$

Mit Stützvektor $\overrightarrow{O B}$ und den Spannvektoren $\overrightarrow{B C}$ und $\overrightarrow{B E}$ ergibt sich für eine Gleichung von $H$ : $H: \overrightarrow{x}=\pmatrix{2\\0\\0}+s \cdot \pmatrix{-2\\8\\0}+t \cdot \pmatrix{0\\0\\4} ; s, t \in \mathbb{R}.$

Mit $s=\dfrac{1}{2}$ und $t=\dfrac{1}{2}$ ergibt sich als weiterer Punkt auf der Seitenfläche $BCFE$ zum Beispiel $(1 \mid 4 \mid 2).$

Die Ebenengleichung $4 x_1+x_2=8$ enthält keine $x_3$ -Koordinate, weshalb die Ebene parallel zur $x_3$ -Achse verläuft.

Punkt $F_4$ berechnen

$\overrightarrow{OF_4}=\pmatrix{0\\4\\12-4} = \pmatrix{0\\4\\8}$

Mittelpunkt $M$ der Strecke $\overline{D E}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{OM} &=& \dfrac{1}{2}\cdot(D+E) \\[5pt] &=& \dfrac{1}{2}\cdot\pmatrix{-2\\0\\4}+\dfrac{1}{2}\cdot\pmatrix{2\\0\\4} \\[5pt] &=& \pmatrix{0\\0\\4} \end{array}$

Vektor $\overrightarrow{M F_4}$ berechnen

$\begin{array}[t]{rlll} \overrightarrow{M F_4} &=& \overrightarrow{OF_4}-\overrightarrow{OM}\\[5pt] &=& \pmatrix{0\\4\\8}-\pmatrix{0\\0\\4} \\[5pt] &=& \pmatrix{0\\4\\4} \end{array}$

Skalarprodukt mit Richtungsvektor der Geraden berechnen

$\begin{array}[t]{rlll} \overrightarrow{M F_4} \circ \vec{r}_g &=& \pmatrix{0\\4\\4} \circ \pmatrix{0\\1\\-1} \\[5pt] &=& 0 \cdot 0 + 4 \cdot 1 + 4 \cdot (-1) \\[5pt] &=& 0 \end{array}$

Somit ist gezeigt, dass die Strecke $\overline{M F_4}$ senkrecht auf der Geraden $g$ steht.

Für jedes $t$ ist $\overline{D E}$ die Basis und $\overline{M F_t}$ die Höhe des gleichschenkligen Dreiecks $E F_t D.$

Da $\overline{M F_t}$ für $t=4$ senkrecht auf $g$ steht, besitzt das Dreieck $E F_t D$ für diesen Wert von $t$ die kleinste Höhe und somit den kleinsten Flächeninhalt.

Aufgabe 3B

Ein Trapez hat zwei gegenüberliegende Seiten, die zwar parallel aber nicht gleich lang sind.

Vektoren der gegegenüberliegenden Seiten berechnen

$\begin{array}[t]{rlll} \overrightarrow{A B} &=& \overrightarrow{OB}-\overrightarrow{OA} \\[5pt] &=& \pmatrix{-4\\1\\a}-\pmatrix{4\\1\\a} \\[5pt] &=& \pmatrix{-8\\0\\0} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{DC} &=& \overrightarrow{OC}-\overrightarrow{OD} \\[5pt] &=& \pmatrix{-5\\0\\0}-\pmatrix{5\\0\\0} \\[5pt] &=& \pmatrix{-10\\0\\0} \end{array}$

Zeigen, dass $\boldsymbol{\overrightarrow{AB}}$ und $\boldsymbol{\overrightarrow{DC}}$ parallel zueinander sind

$\begin{array}[t]{rlll} \overrightarrow{AB} &=& \dfrac{4}{5}\cdot\overrightarrow{DC}\\[5pt] \pmatrix{-8\\0\\0} &=& \dfrac{4}{5}\cdot\pmatrix{-10\\0\\0} \end{array}$

Die anderen zwei Seiten müssen bei einem symmetrischen Trapez gleich lang sein.

Vektoren der zwei Seiten berechnen

$\begin{array}[t]{rlll} \overrightarrow{AD} &=& \overrightarrow{OD}-\overrightarrow{OA} \\[5pt] &=& \pmatrix{5\\0\\0}-\pmatrix{4\\1\\a} \\[5pt] &=& \pmatrix{1\\-1\\-a} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{BC} &=& \overrightarrow{OC}-\overrightarrow{OB} \\[5pt] &=& \pmatrix{-5\\0\\0}-\pmatrix{-4\\1\\a} \\[5pt] &=& \pmatrix{-1\\-1\\-a} \end{array}$

Länge der Vektoren berechnen

$\begin{array}[t]{rlll} \left| \overrightarrow{AD} \right| &=& \sqrt{1^2+(-1)^2+(-a)^2}\\[5pt] &=& \sqrt{2+a^2} \end{array}$

$\begin{array}[t]{rlll} \left| \overrightarrow{BC} \right| &=& \sqrt{(-1)^2+(-1)^2+(-a)^2}\\[5pt] &=& \sqrt{2+a^2} \end{array}$

Somit folgt, dass die Seiten gleich lang sind:

$|\overrightarrow{AD}|=\sqrt{2+a^2}=|\overrightarrow{B C}|$

Die Figur $ABCD$ ist ein Trapez, da die gegenüberliegenden Seiten $\overline{A B}$ und $\overline{D C}$ parallel, aber unterschiedlich lang sind. Die beiden Schenkel $\overline{A D}$ und $\overline{B C}$ sind gleich lang, daher handelt es sich um ein symmetrisches Trapez.

Bei Niedrigwasser gilt $a=-4$ und damit für die Länge der Strecke $|\overrightarrow{A D}|=\sqrt{2+(-4)^2} \approx 4,24.$

Die zusätzlich zu betrachtende Länge beträgt $1,5 \; \text{m}$ , also folgt:

$4,24+1,5 \approx 5,7$

Die Leine muss eine Mindestlänge von etwa $5,7 \;\text{m}$ haben.

Auflösen nach $a_1$ mit dem GTR liefert für den Term $\cos \left(110^{\circ}\right)=\dfrac{\overrightarrow{A B} \circ \overrightarrow{A D}}{|\overrightarrow{A B}| \cdot|\overrightarrow{A D}|}$ die relevante Lösung $a_1 \approx-2,56.$

Parametergleichung der Leine aufstellen

$\overrightarrow{OA}+t \cdot \overrightarrow{A P}=\pmatrix{4\\1\\-4}+t \cdot \pmatrix{3\\-1,5\\4,5}$

Schnittpunkt mit der Ebene $\boldsymbol{y=0}$ berechnen

$\begin{array}[t]{rlll} y(t)&=&0 \\[5pt] 1-1,5 t &=& 0 &\mid\; -1 \\[5pt] -1,5 t &=& -1 &\mid\; : (-1,5) \\[5pt] t &=& \frac{2}{3} \end{array}$

Koordinate $\boldsymbol{z}$ an dieser Stelle berechnen

Setze $t=\frac{2}{3}$ in $z(t)$

$\begin{array}[t]{rlll} z &=& -4 + \dfrac{2}{3} \cdot 4,5 \\[5pt] &=& -1 \end{array}$

Da der Punkt $(x \mid 0 \mid -1)$ unterhalb der Oberkante der Kaimauer liegt (welche bei $z=0$ ist), verläuft die direkte Verbindung der Punkte durch die Kaimauer.
Somit knickt die Leine an der Kante der Kaimauer ab.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?