Flächeninhalt und Umfang eines Kreises

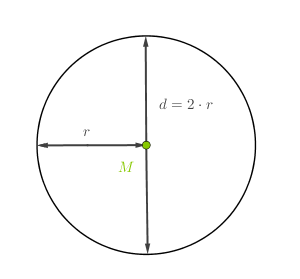
Radius und Durchmesser

Der Radius $(r)$ ist die Länge einer Strecke mit dem Mittelpunkt $(M)$ und einem beliebigen Punkt auf dem Kreisumfang als Endpunkte.
Der Durchmesser $(d)$ beschreibt die Länge einer Strecke, die durch dem Mittelpunkt $(M)$ verläuft und als Endpunkte zwei gegenüberliegende Punkte auf dem Kreisumfang hat.

Abb.: 1

Flächeninhalt

Den Flächeninhalt eines Kreises lässt sich durch die Multiplikation von Pi mit dem Radius zum Quadrat ( $r^2$ ) berechnen.

Umfang

Den Umfang eines Kreises berechnet man aus der Multiplikation von Pi und dem Durchmesser, bzw. der Multiplikation vo Pi und dem doppelten Radius.

Aufgabe 1

Berechne den Umfang und Flächeninhalt. Runde auf die zweite Nachkommestelle.

$\begin{array}[t]{rll} r&=& 46& \\[5pt] \end{array}$

$\begin{array}[t]{rll} d&=& 24& \\[5pt] \end{array}$

$\begin{array}[t]{rll} d&=& 74& \\[5pt] \end{array}$

$\begin{array}[t]{rll} r&=& 13& \\[5pt] \end{array}$

Aufgabe 2

Berechne den Radius und Durchmesser. Runde auf die zweite Nachkommestelle.

$\begin{array}[t]{rll} 54&=& \pi \cdot r^2& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 86&=& \pi \cdot r^2& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 36&=& \pi \cdot d& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 129&=& \pi \cdot r^2& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 13&=& \pi \cdot r^2& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 74&=& 2 \cdot \pi \cdot r& \\[5pt] \end{array}$

Aufgabe 3

Bestimme den Flächeninhalt der gefärbten Flächen mit $\pi = 3,1$ .

Diagramm eines Kreises mit Punkten A, B und C sowie einem rechtwinkligen Dreieck.

Abb.: 1

$r=2$

Diagramm eines Kreises mit Punkten A, B, C, D und E auf einem Koordinatensystem.

Abb.: 2

$r=4$

Grafische Darstellung eines Quadrats mit einem darin eingezeichneten Kreis auf einem Koordinatensystem.

Abb.: 3

$r=3$

Aufgabe 4

Bestimme die Länge der runden Seiten von dem markierten Teil.

Grafik eines Kreises mit Punkten A, B, C und D auf einem Koordinatensystem.

Abb.: 4

$r=1$

Grafik eines Kreises mit Punkten A, B, C, D und E auf einem Koordinatensystem. Teile des Kreises sind grün hervorgehoben.

Abb.: 5

$r=4$

Aufgabe 5

Ein Blumenkübel mit einem Durchmesser von $d = 28 \,\text{cm}$ soll bepflanzt werden. Rechne mit $\pi = 3,1$ .

Wie viele $\,\text{cm}^2$ müssen mit Blumen bepflanzt werden? Runde auf die volle natürliche Zahl.

Eine Blume ist $8 \,\text{cm}^2$ groß. Wie viele Blumen müssen gekauft werden, um den Topf zu bedecken?

Aufgabe 6

Zuhause soll eine Blumentonne mit dem Radius $r=15 \,\text {cm}$ aufgehängt werden.

Berechne den Umfang von dem Topf, sodass dieser mit einem Seil umkleidet werden kann. Kürze auf die zweite Nachkommastelle.

Die Tonne ist $10 \,\text {cm}$ hoch und hat überall den selben Radius. Das Seil ist $2 \,\text{cm}$ dick. Berechne die Länge von dem Seil, wenn es die ganze Blumentonne umkleiden soll ohne Zwischenräume.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

$\begin{array}[t]{rll} r &=& 46 & \\[5pt] A &=& \pi \cdot r^2 &\quad \scriptsize \mid\; einsetzen \\[5pt] A &=& \pi \cdot 46^2 &\\[5pt] A &\approx& 6647,61 & \\[5pt] \end{array}$

$\begin{array}[t]{rll} U &=& 2 \cdot \pi \cdot r&\quad \scriptsize \mid\; einsetzen\\[5pt] U &=& 2 \cdot \pi \cdot 46&\\[5pt] U &\approx& 289,03&\\[5pt] \end{array}$

$\begin{array}[t]{rll} d &=& 24& \\[5pt] A &=& \pi \cdot r^2 &\quad \scriptsize \mid\; einsetzen \\[5pt] A &=& \pi \cdot 12^2 &\\[5pt] A &\approx& 452,39 & \\[5pt] \end{array}$

$\begin{array}[t]{rll} U &=& 2 \cdot \pi \cdot r&\quad \scriptsize \mid\; einsetzen\\[5pt] U &=& 2 \cdot \pi \cdot 12&\\[5pt] U &\approx& 75,40&\\[5pt] \end{array}$

$\begin{array}[t]{rll} d &=& 74& \\[5pt] A &=& \pi \cdot r^2 &\quad \scriptsize \mid\; einsetzen \\[5pt] A &=& \pi \cdot 37^2 &\\[5pt] A &\approx& 4300,84 & \\[5pt] \end{array}$

$\begin{array}[t]{rll} U &=& 2 \cdot \pi \cdot r&\quad \scriptsize \mid\; einsetzen\\[5pt] U &=& 2 \cdot \pi \cdot 37&\\[5pt] U &\approx& 232,48&\\[5pt] \end{array}$

$\begin{array}[t]{rll} r &=& 13& \\[5pt] A &=& \pi \cdot r^2 &\quad \scriptsize \mid\; einsetzen \\[5pt] A &=& \pi \cdot 13^2 &\\[5pt] A &\approx& 530,93 & \\[5pt] \end{array}$

$\begin{array}[t]{rll} U &=& 2 \cdot \pi \cdot r&\quad \scriptsize \mid\; einsetzen\\[5pt] U &=& 2 \cdot \pi \cdot 13&\\[5pt] U &\approx& 81,68&\\[5pt] \end{array}$

Lösung 2

$\begin{array}[t]{rll} 54&=&\pi \cdot r^2 &\quad \scriptsize \mid\; :\pi \\[5pt] r^2&\approx& 17,19 &\quad \scriptsize \mid\;\sqrt{} \\[5pt] r&\approx& 4,15 &\\[5pt] \end{array}$

$\begin{array}[t]{rll} d&=& 2 \cdot r&\quad \scriptsize \mid\; einsetzen \\[5pt] d&=& 2 \cdot 4,15& \\[5pt] d&=& 8,30& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 86&=&\pi \cdot r^2 &\quad \scriptsize \mid\; :\pi \\[5pt] r^2&\approx& 27,37 &\quad \scriptsize \mid\;\sqrt{} \\[5pt] r&\approx& 5,23 &\\[5pt] \end{array}$

$\begin{array}[t]{rll} d&=& 2 \cdot r&\quad \scriptsize \mid\; einsetzen \\[5pt] d&=& 2 \cdot 5,23& \\[5pt] d&=& 10,46& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 36&=&\pi \cdot d&\quad \scriptsize \mid\; :\pi \\[5pt] d&\approx& 11,46 & \\[5pt] \end{array}$

$\begin{array}[t]{rll} r&=& d : 2&\quad \scriptsize \mid\; einsetzen \\[5pt] r&=& 11,46: 2& \\[5pt] r&=& 5,73& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 129&=&\pi \cdot r^2 &\quad \scriptsize \mid\; :\pi \\[5pt] r^2&\approx& 41,06 &\quad \scriptsize \mid\;\sqrt{} \\[5pt] r&\approx& 6,41 &\\[5pt] \end{array}$

$\begin{array}[t]{rll} d&=& 2 \cdot r&\quad \scriptsize \mid\; einsetzen \\[5pt] d&=& 2 \cdot 6,41& \\[5pt] d&=& 12,82& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 13&=&\pi \cdot r^2 &\quad \scriptsize \mid\; :\pi \\[5pt] r^2&\approx& 4,14 &\quad \scriptsize \mid\;\sqrt{} \\[5pt] r&\approx& 2,03 &\\[5pt] \end{array}$

$\begin{array}[t]{rll} d&=& 2 \cdot r&\quad \scriptsize \mid\; einsetzen \\[5pt] d&=& 2 \cdot 2,03& \\[5pt] d&=& 4,06& \\[5pt] \end{array}$

$\begin{array}[t]{rll} 74&=&2 \cdot \pi \cdot r &\quad \scriptsize \mid\; :2\pi \\[5pt] r&\approx& 11,78 &\\[5pt] \end{array}$

$\begin{array}[t]{rll} d&=& 2 \cdot r&\quad \scriptsize \mid\; einsetzen \\[5pt] d&=& 2 \cdot 11,78& \\[5pt] d&=& 23,56& \\[5pt] \end{array}$

Lösung 3

$\begin{array}[t]{rll} r&=& 2 & \\[5pt] A&=& \pi \cdot 2^2&\\[5pt] A&\approx& 12,56 & \\[5pt] \end{array}$

Der Kreis muss in vier gleich große Teile zerteilt werden.

	$1$	$2,$	$5$	$6$	$:$	$4$	$=$	$3$	$,1$	$4$
$\text{-}$	$1$	$2$
		$0$	$5$
	$\text{-}$		$4$
			$1$	$6$
		$\text{-}$	$1$	$6$
			$0$

Jetzt sind nur drei Teile markiert, also musst du das berechnete Ergebnis mit 3 multiplizieren.

$3,14 \cdot 3$ = $9,42$

$\begin{array}[t]{rll} r&=& 4 & \\[5pt] A&=& \pi \cdot 4^2&\\[5pt] A&\approx& 50,27 & \\[5pt] \end{array}$

Man kann die Teile zusammenfassen, sodass die markierte Fläche die Hälfte des Kreises ausfüllt.

$50,27 : 2$ = $25,135$

$\begin{array}[t]{rll} r&=& 3 & \\[5pt] \end{array}$

Zuerst musst du herausfinden, wie lang die Seiten des Quadrates sind.
Hier hilft der Durchmesser des Kreises (d=6cm).
Danach den Flächeninhalt des Quadrats berechnen.

$\begin{array}[t]{rll} A_{Quadrat}&=& 6 \cdot 6& \\[5pt] A_{Quadrat}&=& 36& \\[5pt] \end{array}$

Jetzt den Flächeninhalt des Kreises berechnen.

$\begin{array}[t]{rll} A_{Kreis}&=& \pi \cdot 3^2 &\\[5pt] A_{Kreis}&=& 28,27 &\\[5pt] \end{array}$

Nun den Flächeninhalt des Kreises von dem Flächeninhalt des Quadrates subtrahieren.

$\begin{array}[t]{rll} A_{gesucht}&=& 36 - 28,27 & \\[5pt] A_{gesucht}&=& 7,73 & \\[5pt] \end{array}$

Lösung 4

$\begin{array}[t]{rll} r&=& 1 & \\[5pt] U&=& 2 \cdot \pi \cdot 1 & \\[5pt] U&\approx& 6,28 & \\[5pt] \end{array}$

Nun ist aber nur nach der Hälfte des Umfangs gefragt, also musst du das Ergebnis halbieren.

$\begin{array}[t]{rll} U_{gesucht}&=& 6,28 : 2 & \\[5pt] U_{gesucht}&=& 3,14 & \\[5pt] \end{array}$

$\begin{array}[t]{rll} U&=& 2 \cdot \pi \cdot 4 & \\[5pt] U&\approx& 25,13 & \\[5pt] \end{array}$

Wenn man beide Teile zusammenzieht, füllt der markierte Teil die Hälfte des Kreises aus, also musst du das Ergebnis halbieren.

$\begin{array}[t]{rll} U_{gesucht}&=& 25,13 : 2 &\\[5pt] U_{gesucht}&\approx& 12,57&\\[5pt] \end{array}$

Lösung 5

Du musst zuerst den Radius berechnen.

$28 : 2 = 14$

Jetzt kannst du den Flächeninhalt berechnen.

$\begin{array}[t]{rll} A&=& \pi \cdot r^2 & \\[5pt] A&=& 3,1 \cdot 14^2 & \\[5pt] A&=& 607,6 & \\[5pt] \end{array}$

Es müssen $607,6\,\text{cm}^2$ bepflanzt werden.

Die Blumenfläche von der Gesamtfläche dividieren.

	$6$	$0$	$7$	$,6$	$:$	$8$	$=$	$7$	$5$	$,9$	$5$
$\text{-}$	$5$	$6$
		$4$	$7$
	$\text{-}$	$4$	$0$
			$7$	$,6$
		$\text{-}$	$7$	$,2$
				$4$	$0$
			$\text{-}$	$4$	$0$
					$0$

Es müssen $76$ Blumen gekauft werden, sodass alles bedeckt ist.

Lösung 6

$\begin{array}[t]{rll} U &=& 2 \cdot \pi \cdot 15& \\[5pt] U &=& 94,25 \end{array}$

Der Umfang beträgt $94,25\,\text{cm}$ .

Wie häufig muss das Seil um den Topf gespannt werden?
Das Ergebnis dafür erreichst du durch das Dividieren der Dicke des Seils von der Höhe der Tonne.

$\begin{array}[t]{rll} 10 : 5 &=& 2 & \\[5pt] \end{array}$

Nun musst du den Umfang mit der Anzahl der Umdrehungen multiplizieren.

$\begin{array}[t]{rll} 94,25 \cdot 5 &=& 471,25 & \\[5pt] \end{array}$

Das Seil wäre $471,25\,\text{cm}$ lang.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?