1 Analysis – Pflichtaufgabe

Gegeben ist die Funktion $f$ mit $f(x)=\frac{3}{100}\cdot x^3-\frac{91}{100}\cdot x^2+9\cdot x-26$ und $x\in\mathbb{R}.$

1.1

Gib für $f$ die Nullstelle sowie das Verhalten für $x\to -\infty$ und für $x\to +\infty$ an.

(3 BE)

1.2

Die Funktion $f$ hat genau eine Wendestelle.

Weise nach, dass $x=\frac{91}{9}$ diese Stelle ist.

(2 BE)

1.3

Ermittle das Intervall, das alle Werte von $x$ enthält, für die $f$ monoton fallend ist.

(2 BE)

1.4

$F$ ist eine Stammfunktion von $f.$

Berechne für $a\gt0$ alle Lösungen der Gleichung $F\left(\frac{91}{9}\right)-F\left(\frac{91}{9}-a\right)=10.$

Skizziere außerdem eine graphische Lösung dieser Gleichung.

(4 BE)

Beim Laufen bildet sich im menschlichen Körper Laktat (Milchsäure). Die Laktatkonzentration ist abhängig von der Belastung der Muskeln. Die Messung der Laktatkonzentration im Blut dient zur Diagnostik der Ausdauerleistung und zur Trainingsplanung. Ein Ziel der Diagnostik ist dabei die Bestimmung der Laktatschwelle. Vereinfacht bezeichnet diese die höchste Laufgeschwindigkeit, die langfristig durchgehalten werden kann, z. B. bei einem Marathon.

Für einen Läufer A kann auf Grundlage seiner Messwerte die Laktatkonzentration durch die Funktion $f$ im Intervall $7\leq x\leq 18$ modelliert werden.

Dabei ist $x$ die Laufgeschwindigkeit in $\text{km/h}$ (Kilometer pro Stunde) und $f(x)$ die Laktatkonzentration in $\text{mmol/L}$ (Millimol pro Liter). Den in der Abbildung dargestellten Graphen von $f$ nennt man Laktatkurve des Läufers A.

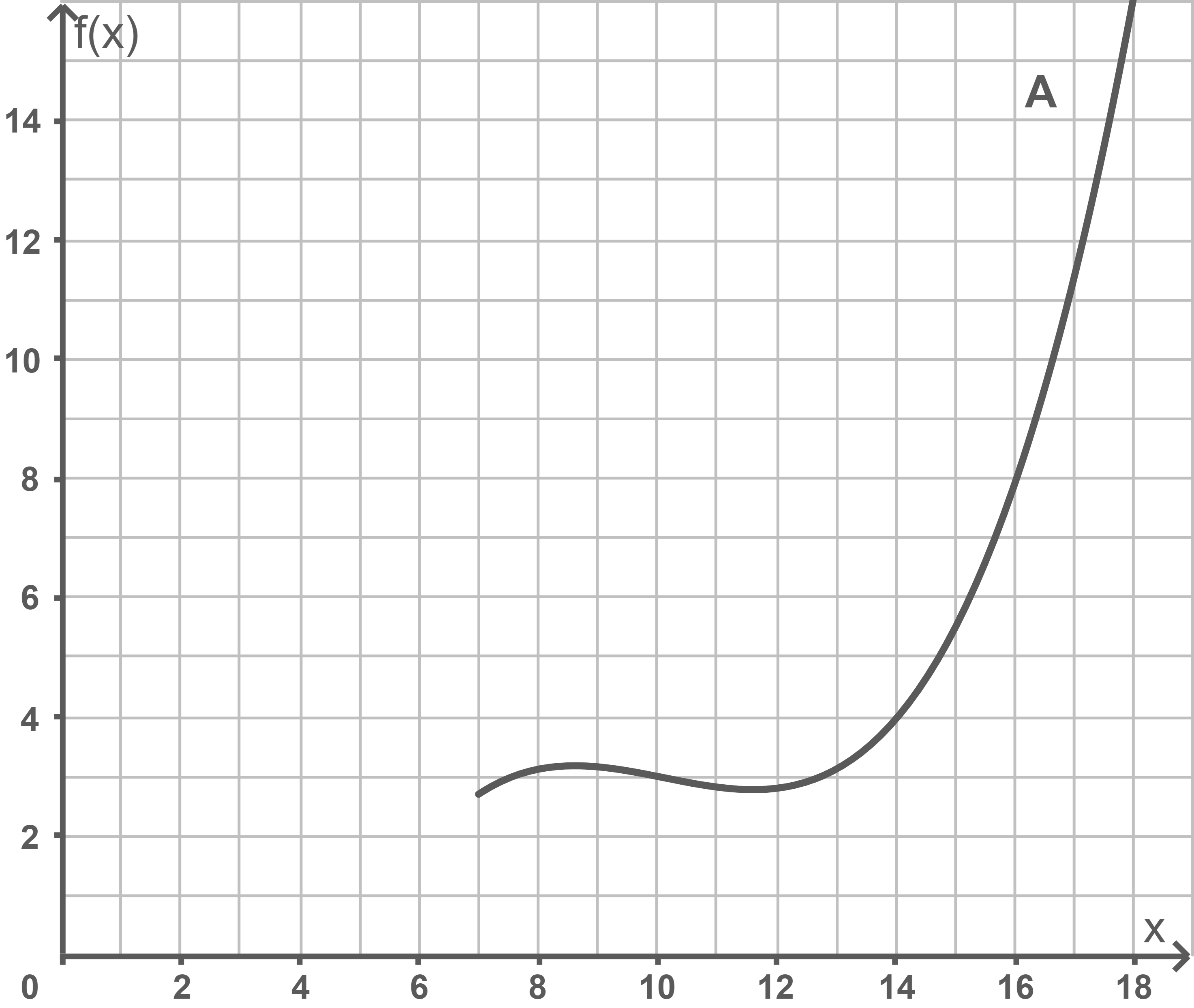
Graph einer Funktion f(x) mit gekennzeichnetem Punkt A und Achsenbeschriftung.

1.5

Zur Ermittlung der individuellen Laktatschwelle existieren in der Sportmedizin verschiedene mathematische Methoden:

Methode 1:	Bei Erreichung von genau $4\;\text{mmol}$ Laktat pro Liter Blut.
Methode 2:	Der Anstieg der Laktatkurve erreicht den Wert $1.$

Berechne und vergleiche für den Läufer A für beide Methoden die Laktatschwelle.

(5 BE)

1.6

Im Rahmen einer Leistungsdiagnostik für einen Läufer B ergaben sich die in der Tabelle dargestellten Messwerte.

Laufgeschwindigkeit $\color{#FFFFFF}{x}$ in $\color{#FFFFFF}{\text{km/h}}$	Laktatkonzentration in $\color{#FFFFFF}{\text{mmol/L}}$
$7$	$2,5$
$8$	$2,8$
$10$	$3,1$
$14$	$4,5$
$18$	$10,6$

1.6.1

Bestimme mithilfe der ersten vier Messwertpaare eine Gleichung einer ganzrationalen Funktion dritten Grades, die die Laktatkurve für Läufer B modelliert.

Zeige, dass die ermittelte Modellfunktion auch eine gute Näherung für das letzte Wertepaar liefert.

Term zur Kontrolle: $0,012x^3-0,35x^2+3,5x-9,07$

(4 BE)

1.6.2

Ergänze in der Abbildung die modellierte Laktatkurve für Läufer B für $7\leq x\leq 18$ sowie die Messwerte.

(3 BE)

1.6.3

Bewerte anhand eines Kriteriums, welcher der Läufer A und B den besseren Trainingszustand aufweisen könnte.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Nullstelle bestimmen
Um die Nullstelle der Funktion $f$ zu bestimmen, wird $f(x)=0$ gesetzt. Auflösen der Gleichung nach $x$ mit dem solve-Befehl des CAS liefert $x=5.$

Verhalten im Unendlichen
Bei $f$ handelt es sich um eine kubische Funktion (Polynom dritten Grades), dessen Leitkoeffizient $\tfrac{3}{100}$ beträgt. Diese beiden Eigenschaften bestimmen das Verhalten von $f$ im Unendlichen.

Für $x\to-\infty$ gilt:

$\begin{array}[t]{rlll} \lim\limits_{x\to-\infty}f(x)&=&\lim\limits_{x\to-\infty}\dfrac{3}{100}x^3 \\[5pt] &=&\dfrac{3}{100}\cdot(-\infty) \\[5pt] &=&-\infty \end{array}$

Für $x\to+\infty$ gilt:

$\begin{array}[t]{rlll} \lim\limits_{x\to+\infty}f(x)&=&\lim\limits_{x\to+\infty}\dfrac{3}{100}x^3 \\[5pt] &=&\dfrac{3}{100}\cdot\infty \\[5pt] &=&\infty \end{array}$

1.2

An einem Wendepunkt gilt die notwendige Bedingung $\(f$ Mit dem CAS folgt für die ersten beiden Ableitungen von $f:$

$\(f$

Lösen von $\(f$ mit dem solve-Befehl des CAS liefert $x=\frac{91}{9}.$ Laut der Aufgabenstellung hat die Funktion $f$ genau eine Wendestelle, somit kann die Überprüfung der hinreichenden Bedingung hier vernachlässigt werden.

1.3

Wenn $f$ monoton fallend ist, gilt für die erste Ableitung $\(f$ Lösen der Ungleichung mit dem solve-Befehl des CAS liefert:

$-\dfrac{\sqrt{181}}{9}+\dfrac{91}{9}\leq x\leq\dfrac{\sqrt{181}}{9}+\dfrac{91}{9}$

Das Intervall, das alle Werte von $x$ enthält, für die $f(x)$ monoton fallend ist, ist somit gegeben durch $\left[-\tfrac{\sqrt{181}}{9}+\tfrac{91}{9},\;\tfrac{\sqrt{181}}{9}+\tfrac{91}{9}\right].$

1.4

Wert von $\boldsymbol{a}$ berechnen
$F\left(\dfrac{91}{9}\right)-F\left(\dfrac{91}{9}-a\right)=10$

Mit dem CAS kann die Stammfunktion $F$ bestimmt werden:

$F(x)=\dfrac{3}{400}x^4-\dfrac{91}{300}x^3+\dfrac{9}{2}x^2-26x$

Auflösen der Gleichung nach $a$ mit dem CAS liefert:

$\begin{array}[t]{rlll} a_1&\approx&3,3 \\[3pt] a_2&\approx&6,6 \end{array}$

Skizze der graphischen Lösung

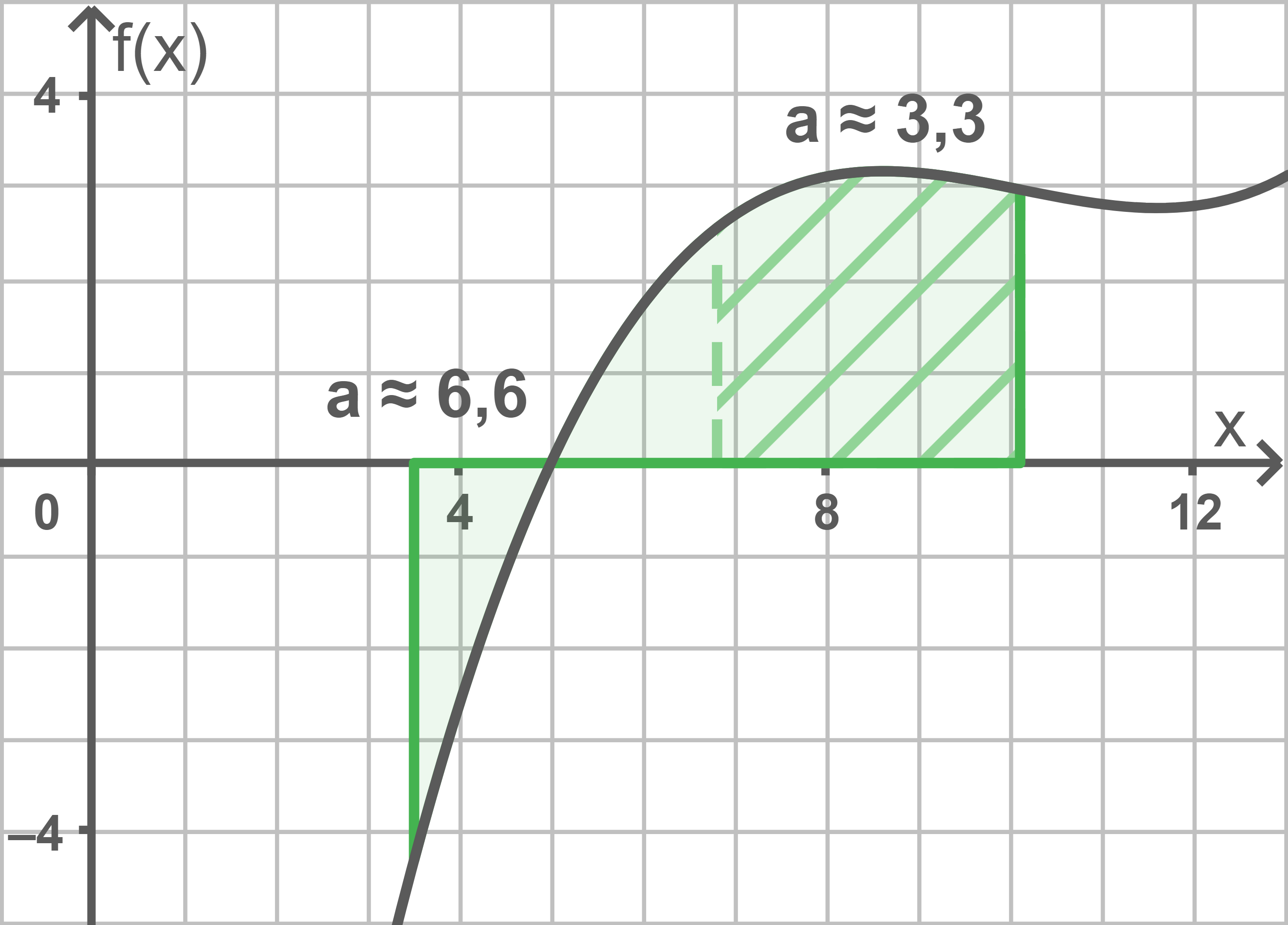
Graf einer Funktion mit markierten Bereichen und Achsenbeschriftungen.

1.5

Methode 1 entspricht der Gleichung $f(x)=4.$ Für Methode 2 gilt, dass die Ableitung $\(f$ sein soll. Auflösen beider Gleichungen mit dem solve-Befehl des CAS ergibt:

Methode 1: $\begin{array}[t]{rlll} x&\approx&14,0\;\dfrac{\text{km}}{\text{h}} \end{array}$

Methode 2: $\begin{array}[t]{rlll} x_1&\approx&13,8\;\dfrac{\text{km}}{\text{h}} \\[5pt] x_2&\approx&6,5\;\dfrac{\text{km}}{\text{h}} \end{array}$

Die Lösung $x_2\approx6,5\;\tfrac{\text{km}}{\text{h}}$ für Methode 2 entfällt hierbei, weil sie kleiner als $7$ ist und somit außerhalb des Intervalls $7\leq x\leq18$ der Funktion $f$ liegt. Beide Ergebnisse für die Laktatschwelle entsprechen einander näherungsweise.

1.6

1.6.1

Bestimmung einer ganzrationalen Modellfunktion dritten Grades
$g(x)=a\cdot x^3+b\cdot x^2+c\cdot x+d$

Mithilfe der ersten vier Messwertpaare kann ein Gleichungssystem aufgestellt werden:

$\begin{array}[t]{rlll} g(7)&=&2,5; \\[3pt] g(8)&=&2,8; \\[3pt] g(10)&=&3,1; \\[3pt] g(14)&=&4,5 \end{array}$

$\begin{array}{lrll} \text{I}\quad&2,5&=&343a+49b+7c+d \\ \text{II}\quad&2,8&=&512a+64b+8c+d \\ \text{III}\quad&3,1&=&1000a+100b+10c+d \\ \text{IV}\quad&4,5&=&2744a+196b+14c+d \end{array}$

Auflösen des Gleichungssystem mit dem CAS ergibt:

$\begin{array}[t]{rlll} a&\approx&0,012; \\[3pt] b&\approx&-0,348; \\[3pt] c&\approx&3,502; \\[3pt] d&\approx&-9,067 \end{array}$

Somit lautet die Funktionsgleichung der Modellfunktion: $g(x)=0,012x^3-0,348x^2+3,502x-9,067$

Überprüfung für das letzte Wertepaar
Um zu zeigen, dass die ermittelte Modellfunktion auch für das fünfte Wertepaar eine gute Näherung liefert, wird der Funktionswert von $g(x)$ an der Stelle $x=18$ berechnet. Ausrechnen mit dem CAS liefert:

$g(18)\approx10,8$

Dies entspricht näherungsweise der gemessenen Laktatkonzentration von $10,6\;\text{mmol}/\text{L}$ des Läufers B.

1.6.2

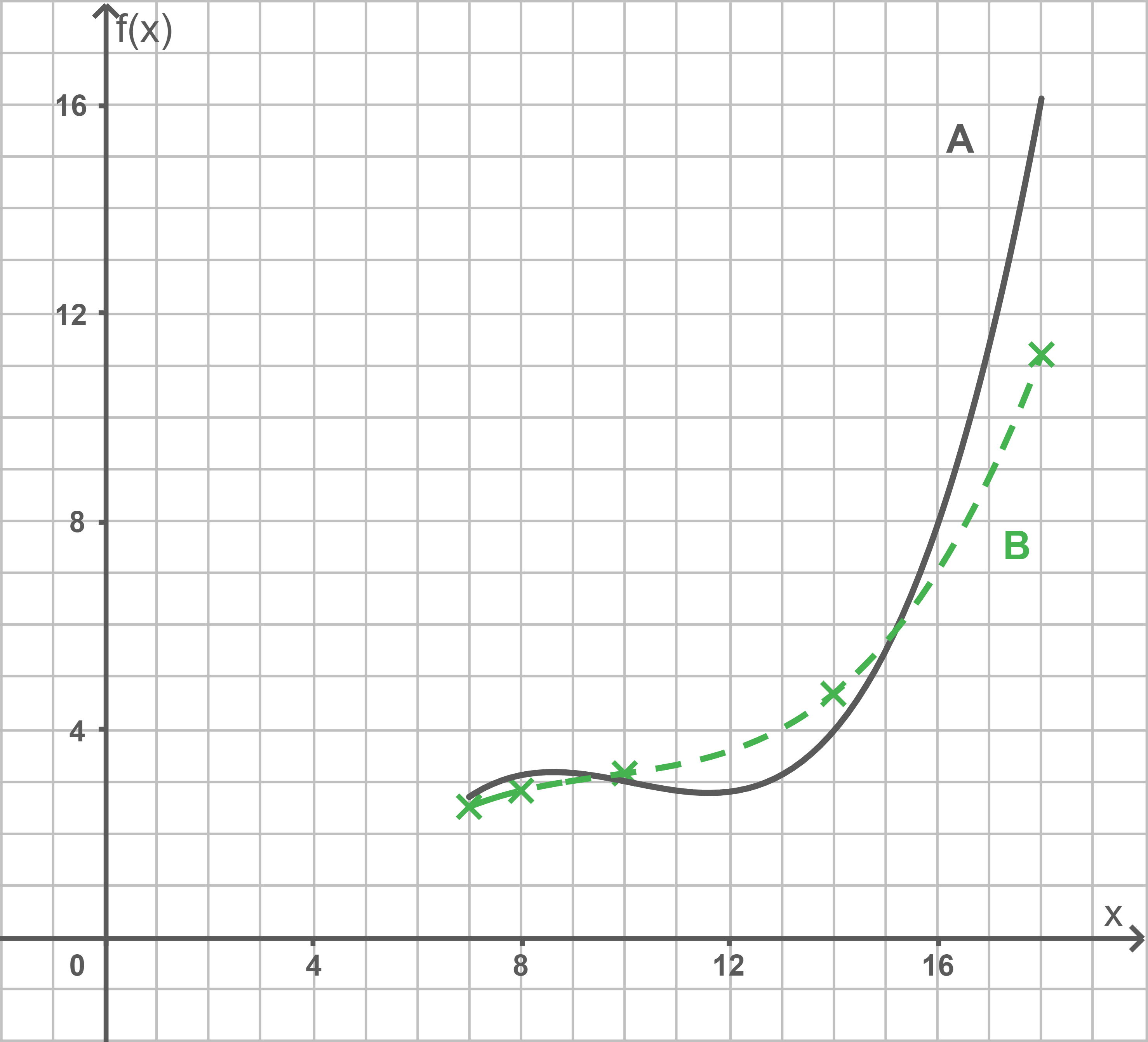
Graph einer Funktion mit Punkten A und B, Gitterlinien im Hintergrund, grüne gestrichelte Linie.

1.6.3

Im direkten Vergleich erreicht Läufer A die Laktatschwelle von $4\;\text{mmol}/\text{L}$ bei einer höheren Laufgeschwindigkeit als Läufer B. Somit könnte Läufer A den besseren Trainingszustand aufweisen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?