3 Analytische Geometrie – Wahlaufgabe

Eine Brücke mit einem ICE-Gleis überspannt ein Tal. Das Gleis geht unmittelbar im Anschluss dieser Brücke jeweils in einem Tunnel weiter (vgl. Abbildung). Das geradlinig verlaufende Gleis verläuft im Modell entlang der Gerade $g$ mit $g:\overrightarrow{x}=\pmatrix{1\\-5,75\\2}+t\cdot\pmatrix{3\\32\\1}$ und $t\in\mathbb{R}.$

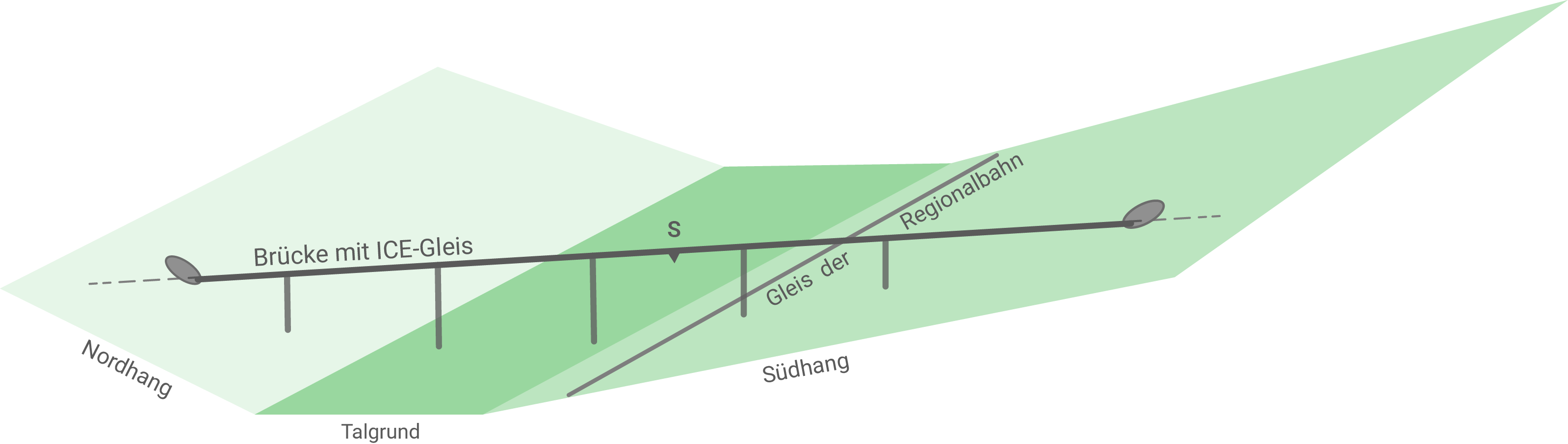
Schematische Darstellung einer Brücke mit Gleisen in einem Hang.

In einem kartesischen Koordinatensystem beschreibt die $xy$ -Ebene den horizontal verlaufenden Talgrund. Der Punkt $P(1\mid-5,75\mid2)$ stellt den Beginn der Brücke im Nordhang, der Punkt $Q(2,5\mid10,25\mid2,5)$ das Ende der Brücke im Südhang dar.

Eine Längeneinheit im Koordinatensystem entspricht $10$ Meter in der Realität.

3.1

Ein ICE befährt die Brücke vom Nordhang kommend in Richtung Südhang.

3.1.1

Berechne die Länge der Brücke in Metern.

(3 BE)

3.1.2

Begründe, dass der ICE beim Überqueren der Brücke einen Anstieg bewältigt.

(1 BE)

3.2

Der ebene Nordhang liegt im Modell in der Ebene mit der Gleichung $3x+90y+172z=d.$

3.2.1

Berechne den Wert von $d.$

(1 BE)

3.2.2

Berechne die Größe des Neigungswinkels des Nordhangs gegenüber dem horizontal verlaufenden Talgrund.

(3 BE)

3.3

Gegeben ist eine weitere Gerade $h$ mit $h:\overrightarrow{x}=\pmatrix{-8\\2,25\\0,5}+s\cdot\pmatrix{3\\0\\0,01}$ und $s\in\mathbb{R}.$

Mithilfe der Gerade $h$ wird das Gleis einer Regionalbahn beschrieben. Dieses Gleis verläuft auf dem Südhang unterhalb der Brücke.

An der Brücke ist ein Sensor zur Brückenüberwachung angebracht. Seine Position ist in der Abbildung mit $S$ bezeichnet. Dieser Sensor befindet sich genau senkrecht oberhalb des Gleises der Regionalbahn.

3.3.1

Gib die besondere Lage der Gerade $h$ bezüglich der $xz$ -Ebene an.

(1 BE)

3.3.2

Im Modell können die Koordinaten des Punktes, der die Position des Sensors beschreibt, mit folgendem Ansatz berechnet werden: $\pmatrix{1\\-5,75\\2}+t\cdot\pmatrix{3\\32\\1}=\pmatrix{x\\2,25\\z}$

Erläutere den zugrundeliegenden geometrischen Sachverhalt.

(3 BE)

3.3.3

Berechne im Modell die Koordinaten des Sensors $S.$

Weise rechnerisch nach, dass der Sensor gleich weit von den Enden der Brücke entfernt ist.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

3.1

3.1.1

Die Länge der Brücke entspricht dem Betrag des Vektors $\overrightarrow{PQ},$ wobei eine Längeneinheit im Koordinatensystem $10$ Meter in der Realität entspricht.

$\begin{array}[t]{rlll} \overrightarrow{PQ}=\overrightarrow{Q}-\overrightarrow{P}&=&\pmatrix{2,5-1\\10,25-(-5,75)\\2,5-2} \\[5pt] &=&\pmatrix{1,5\\16\\0,5} \end{array}$

$\left\vert\overrightarrow{PQ}\right\vert=\sqrt{1,5^2+16^2+0,5^2}\approx16,08$

Somit hat die Brücke eine Länge von rund $161\;\text{m}.$

3.1.2

Die $z$ -Koordinate von $Q$ ist größer als die $z$ -Koordinate von $P.$ Weil der Zug vom Nordhang kommend die Brücke überquert, bewältigt er somit einen Anstieg.

3.2

3.2.1

Einsetzen der Koordinaten von $P$ in die Ebenengleichung des Nordhangs liefert:

$\begin{array}[t]{rlll} 3\cdot1+90\cdot(-5,75)+172\cdot2&=&d \\[5pt] -170,5&=&d \end{array}$

3.2.2

Der Talgrund liegt parallel zur $xy$ -Ebene. Dementsprechend lautet ein möglicher Normalenvektor $\overrightarrow{n_{\text{T}}}=\pmatrix{0\\0\\1}.$

Der Neigungswinkel des Nordhangs gegenüber dem Talgrund kann mithilfe des Skalarprodukts zwischen dem Normalenvektor $\overrightarrow{n_{\text{N}}}$ des Nordhangs und dem Normalenvektor $\overrightarrow{n_{\text{T}}}$ des Talgrunds berechnet werden:

$\begin{array}[t]{rlll} \mathrm{cos}\;(\varphi)&=&\dfrac{\overrightarrow{n_{\text{N}}}\circ\overrightarrow{n_{\text{T}}}}{\left\vert\overrightarrow{n_{\text{N}}}\right\vert\cdot\left\vert\overrightarrow{n_{\text{T}}}\right\vert} \\[5pt] \mathrm{cos}\;(\varphi)&=&\dfrac{\pmatrix{3\\90\\172}\circ\pmatrix{0\\0\\1}}{\left\vert\pmatrix{3\\90\\172}\right\vert\cdot1} \\[5pt] \mathrm{cos}\;(\varphi)&=&\dfrac{172}{\sqrt{3^2+90^2+172^2}}\\[5pt] \varphi&=&\mathrm{cos}^{-1}\left(\dfrac{172}{\sqrt{37693}}\right) \\[5pt] \varphi&\approx&28^\circ \end{array}$

3.3

3.3.1

Die $y$ -Koordinate des Richtungsvektors der Geraden $h$ ist gleich $0$ . Daher verläuft $h$ parallel zur $xz$ -Ebene.

3.3.2

Aufgrund der parallelen Lage der Geraden $h$ bezüglich der $xz$ -Ebene gilt $y=2,25$ für jeden Punkt von $h.$ Jeder Punkt senkrecht darüber, also auch der gesuchte von $g,$ hat ebenfalls die $y$ -Koordinate $2,25.$

3.3.3

Berechnung der Koordinaten des Sensors
$\pmatrix{1\\-5,75\\2}+t\cdot\pmatrix{3\\32\\1}=\pmatrix{x\\2,25\\z}$

$t$ kann durch die $y$ -Koordinaten berechnet werden:

$-5,75+32\cdot t=2,25$

Auflösen der Gleichung nach $t$ mit dem solve-Befehl des CAS liefert:

$t=\dfrac{1}{4}=0,25$

Daraus folgt für die $x$ - und $z$ -Koordinaten:

$x=1+3\cdot0,25=1,75$

$z=2+1\cdot0,25=2,25$

Somit hat der Sensor die Koordinaten $S(1,75\mid2,25\mid2,25)$ im Modell.

Lage des Sensors zu den Enden der Brücke nachweisen

$\begin{array}[t]{rlll} \overrightarrow{M_{\overline{PQ}}}&=&\overrightarrow{OP}+\dfrac{1}{2}\cdot\overrightarrow{PQ} \\[5pt] &=&\pmatrix{1\\-5,75\\2}+\dfrac{1}{2}\cdot\pmatrix{1,5\\16\\0,5} \\[5pt] &=&\pmatrix{1,75\\2,25\\2,25} \end{array}$

Somit hat der Mittelpunkt der Strecke $\overline{PQ}$ die Koordinaten $M_{\overline{PQ}}(1,75\mid2,25\mid2,25).$ Da die Koordinaten des Sensors $S$ mit diesen übereinstimmen, liegt der Sensor gleich weit von den Enden der Brücke entfernt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?