B2 – Analysis
Betrachtet wird die Schar der in definierten Funktionen
mit
Abbildung 1 zeigt einen Graphen der Schar.
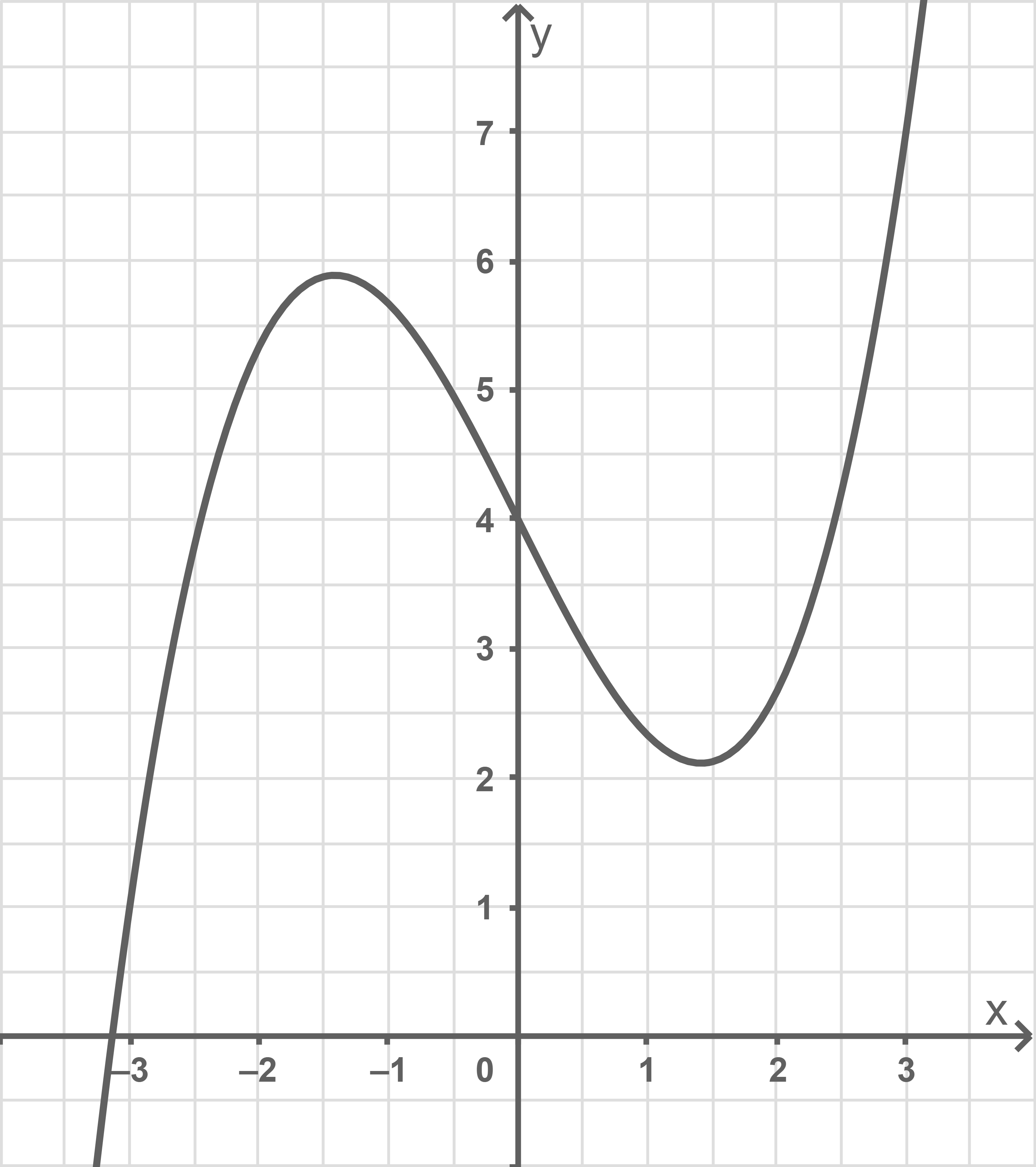
Der Graph in Abbildung 1 verläuft durch den Punkt
Begründe rechnerisch, dass es sich um den Graphen von handelt.
Zeige rechnerisch, dass jeder Graph der Schar genau einen Wendepunkt besitzt, und gib dessen Koordinaten an.
Berechne denjenigen Wert von für den
gilt.
Betrachtet wird im Folgenden die in definierte Funktion
Die Funktion entspricht der Funktion
der Schar, Abbildung 1 zeigt somit den Graphen
von
Dieser ist symmetrisch bezüglich des Punkts
Die Tangente an
im Punkt
wird mit
bezeichnet;
ist eine Gleichung von
Zeige rechnerisch anhand geeigneter Termumformungen, dass für alle
gilt.
Begründe mithilfe dieses Zusammenhangs, dass und
neben
genau einen weiteren gemeinsamen Punkt besitzen.
Betrachtet wird die Gleichung mit
Für
besitzt diese Gleichung genau eine Lösung.
Untersuche grafisch mithilfe von Abbildung 1, wie viele Lösungen diese Gleichung für besitzt.
Die Länge einer Fahrstrecke, die ein Elektroauto mit vollständig geladener Batterie ohne erneutes Aufladen unter bestimmten Bedingungen zurücklegen kann, wird als Nennreichweite des Elektroautos bezeichnet und ist für jedes Elektroauto ein fester Wert. Die tatsächliche Reichweite hängt von vielen Faktoren ab; im Folgenden wird ausschließlich die Abhängigkeit von der Außentemperatur betrachtet.
Diese Abhängigkeit kann für eine Vielzahl von Elektroautos modellhaft im Intervall durch eine Funktion
beschrieben werden. Dabei ist
die Außentemperatur in
und
der Quotient aus der tatsächlichen Reichweite eines Elektroautos und dessen Nennreichweite.
Abbildung 2 zeigt den Graphen der Funktion Hat also
beispielsweise für eine bestimmte Außentemperatur den Wert
so beträgt die tatsächliche Reichweite eines Elektroautos bei dieser Außentemperatur
seiner Nennreichweite. Im Folgenden werden nur Temperaturen im Bereich von
bis
sowie Elektroautos betrachtet, bei denen der durch die Funktion
beschriebene Zusammenhang gilt.
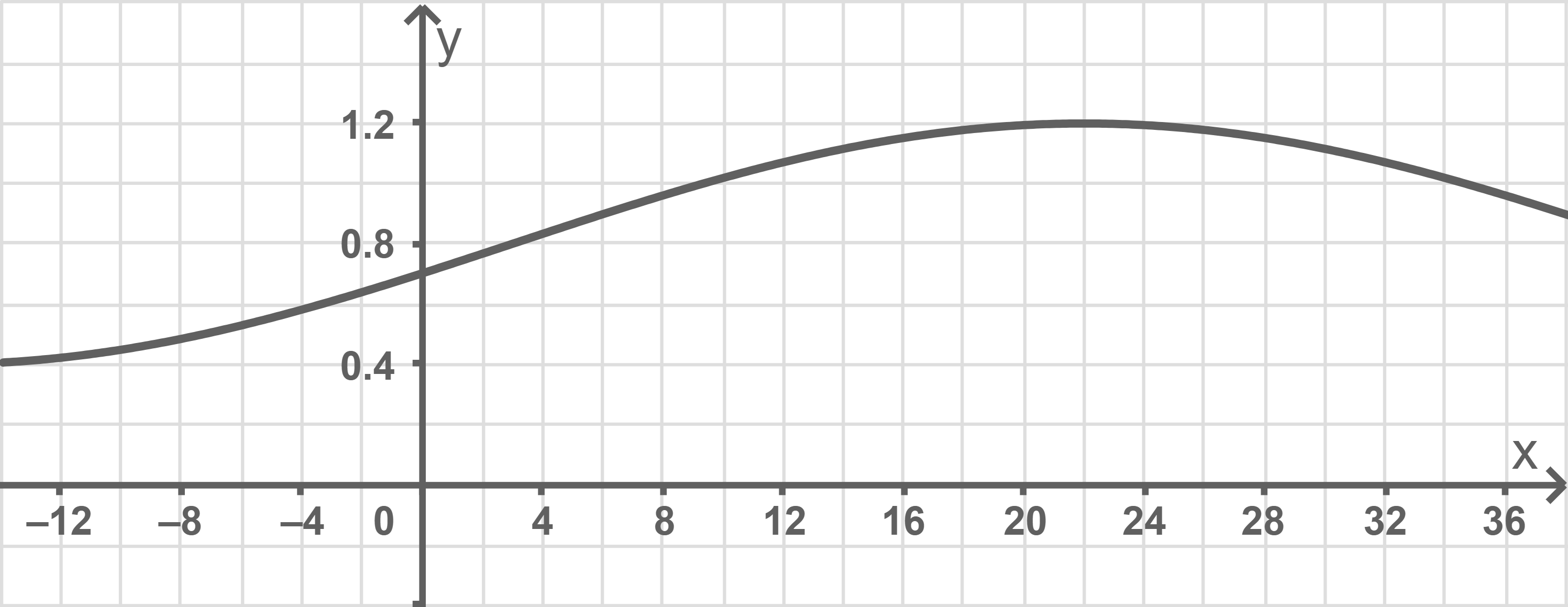
Gib anhand von Abbildung 2 die Koordinaten des Hochpunkts des Graphen von an.
Beschreibe die Bedeutung des Hochpunkts und seiner Koordinaten im Sachzusammenhang.
Die Nennreichweite eines Elektroautos beträgt
die Nennreichweite eines Elektroautos
beträgt
Bestimme mithilfe von Abbildung 2 eine Außentemperatur, bei der das Elektroauto dieselbe tatsächliche Reichweite besitzt wie das Elektroauto
bei einer Außentemperatur von
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Somit handelt es sich um den Graphen von
Für die ersten drei Ableitungen von gilt:
1. Schritt: Notwendige Bedingung für Wendestellen anwenden
2. Schritt: Hinreichende Bedingung für Wendestellen überprüfen
DaSomit besitzen alle Graphen der Schar
3. Schritt: Koordinaten angeben
Die Koordinaten des Wendepunkts jedes Graphen der Schar sind somit durch
gegeben.
Zudem gilt:
Damit gilt die Gleichheit aus der Aufgabenstellung. Der Graph und
besitzen nur an den Stellen
und
gemeinsame Punkte, denn für diese Werte wird die rechte Seite der Gleichung nach dem Satz des Nullprodukts Null und somit auch die linke Seite
Da die
-Koordinate von
durch
gegeben ist, existiert somit genau ein weiterer gemeinsamer Punkt.
Für ergibt sich:
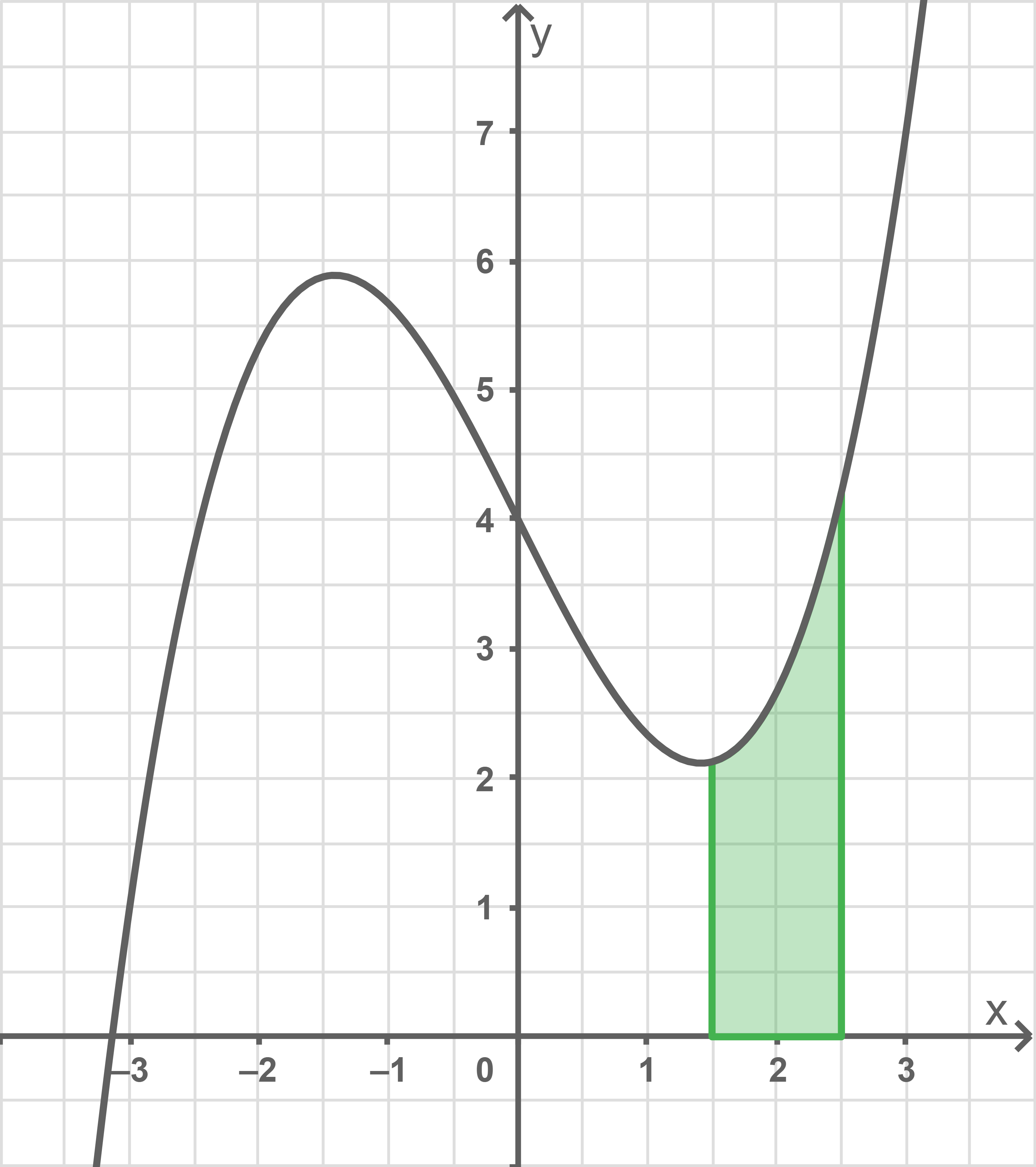
Der Wert der Integrals für ist kleiner als
da die markierte Fläche ca.
Kästchen beträgt, und somit deutlich weniger, als die zu
äquivalenten
Da der Graph von für
allerdings streng monoton steigt, wird auch der Wert des Integrals für steigendes
immer größer. Somit existiert genau ein Wert
der die in der Aufgabenstellung angegebene Gleichung löst.
Koordinaten des Hochpunkts angeben
Bedeutung im Sachzusammenhang beschreiben
Die größte tatsächliche Reichweite des Elektroautos wird bei einer Außentemperatur vonDie tatsächliche Reichweite des Elektroautos ist durch den Achsenabschnitt des Graphen in Abbildung 2 multipliziert mit der Nennreichweite gegeben und beträgt somit ca.
Somit folgt:
Mit Hilfe der Abbildung folgt, dass z.B. bei
gilt. Eine mögliche Außentemperatur ist somit durch ca.
gegeben.