A1 - Analysis

Auf einem See breitet sich eine Algenart aus. Zu Beginn der Beobachtung ist etwa eine Fläche von $0,1\,\text{a}$ des Sees mit Algen bedeckt ( $\text{a}$ steht für die Flächeneinheit $\text{Ar}$ , $1\,\text{a}$ entspricht einem Flächeninhalt von $100\,\text{m}^2$ ). Nach zwei Monaten sind bereits $3\,\text{a}$ des Sees mit Algen bedeckt.
Das weitere Wachstum soll prognostiziert werden. Dafür liegen drei unterschiedliche Modelle $A$ , $B$ und $C$ vor.

Im Modell $A$ wird der Inhalt der mit Algen bedeckten Fläche durch die Funktion $f$ mit den Parametern $r$ und $k$ beschrieben mit $f(t)= r\cdot \mathrm e^{k\cdot t}$ , $t \geq 0$ , $r,k \gt 0$ .
Dabei gilt:

$t:$

Zeit in Monaten nach Beginn der Beobachtung

$f(t):$

Inhalt der mit Algen bedeckten Fläche in $\,\text{a}$

1.1

Bestimme die zu den oben genannten Werten passenden Parameter $r$ und $k$ .

(4 BE)

1.2

Ermittle unter Verwendung der Ergebnisse aus Aufgabe 1.1 für die Gleichung $f(t)= r\cdot \mathrm e^{k\cdot t} = r\cdot (1+p)^t$ den Wert von $p$ .
Deute diesen Wert im Sachzusammenhang.

Falls du den Wert des Parameters $k$ in Aufgabe 1.1 nicht bestimmen konntest, verwende als Ersatzwert $k = 1,71$ .

(3 BE)

Modell $B$ prognostiziert ein Wachstum, bei dem die Änderungsrate des Inhalts der mit Algen bedeckten Fläche in Abhängigkeit von der Zeit $t$ näherungsweise durch die Funktion $g$ mit $g(t)= \left(-0,5t^2 +t+2\right)\cdot \mathrm e^{-0,5t}$ , $t \geq 0$ , beschrieben wird.
Dabei gilt:

$t:$

Zeit in Monaten nach Beginn der Beobachtung

$f(t):$

Änderungsrate in $\,\text{a}$ pro Monat

2.1

Berechne für $t \geq 0$ die Null- und Extremstellen von $g$ . Die zweite Ableitung

Ableitung anzeigen

kann ohne Herleitung verwendet werden.

(11 BE)

2.2

Deute die in Aufgabe 2.1 berechneten Null- und Extremstellen im Sachzusammenhang.

(5 BE)

2.3

In Material 1 ist ein Ansatz zur Ermittlung der Stammfunktionen von $g$ angegeben.
Benenne die verwendete Integrationsmethode und wende die Methode erneut an, um die Herleitung der Stammfunktionen von $g$ zu vervollständigen.

[zur Kontrolle: $G(t) = \left(t^2+2t\right)\cdot \mathrm e^{-0,5\cdot t} +C$ ]

Material 1 anzeigen

(5 BE)

2.4

Untersuche, unter welchen Bedingungen Modell $B$ näherungsweise zu den im einleitenden Text beschriebenen Werten passt.

(3 BE)

Im Modell $C$ wird der Inhalt der mit Algen bedeckten Fläche durch die Funktion $h$ beschrieben mit

$h(t)= \dfrac{0,35}{0,1+3,4\cdot \mathrm e^{-2,66 \cdot t}}$ , $t\geq 0.$

Dabei gilt:

$t:$

Zeit in Monaten nach Beginn der Beobachtung

$f(t):$

Inhalt der mit Algen bedeckten Fläche in \,\text{a}

Bestimme den Grenzwert $\lim\limits_{t\to +\infty} h(t).$
Deute diesen Wert im Sachzusammenhang.

(3 BE)

Im Material 2 sind drei Graphen $\text{(I)}$ , $\text{(II)}$ und $\text{(III)}$ abgebildet, die den Inhalt der mit Algen bedeckten Fläche in Abhängigkeit von der Zeit $t$ über mehrere Monate für die drei Modelle $A$ , $B$ und $C$ beschreiben.
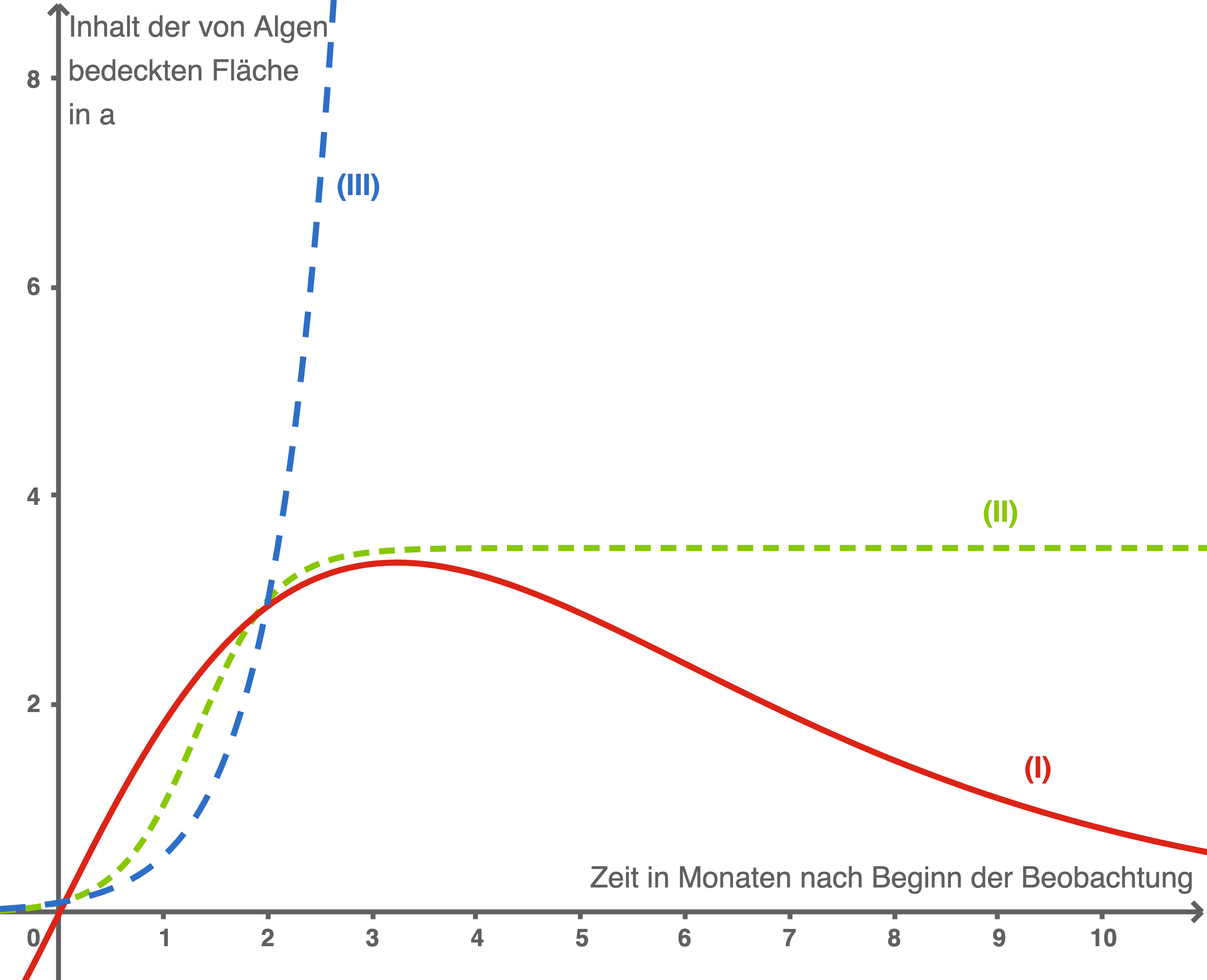
Ordne die Graphen den entsprechenden Modellen zu und erörtere im Sachzusammenhang, wie realistisch die drei Modelle sind.

Material 2

(6 BE)

1.1

Parameterwerte bestimmen

Es gilt $f(t)=r\cdot\mathrm e^{k\cdot t}$ und der Aufgabentext liefert $f(0)=0,1$ und $f(2)=3.$ Einsetzen ergibt:

$\begin{array}{lrll} \text{I}\quad&f(0)&=& 0,1\\ &r\cdot \mathrm e^{k\cdot 0}&=& 0,1\\ &r&=& 0,1 \\[5pt] \text{II}\quad&f(2)&=& 3\\ &r\cdot \mathrm e^{k\cdot 2}&=& 3\\ \end{array}$

$\text{I}$ in $\text{II}$ einsetzen und nach $k$ auflösen:

Rechenweg anzeigen

$k\approx 1,7$

Aus den gegebenen Funktionswerten ergeben sich also $r = 0,1$ und $k\approx 1,7.$

1.2

Wert von $p$ ermitteln

Rechenweg anzeigen

$p \approx 4,5$

Mit den in Aufgabe 1.1 berechneten Parameterwerten ergibt sich $p \approx 4,5.$

Wert im Sachzusammenhang deuten

$f(t)= r\cdot(1+p)^t$ stellt exponentielles Wachstum dar. $p$ gibt die Wachstumsrate an, also den Prozentsatz, um den die betrachtete Größe pro Zeiteinheit zunimmt.

Im Sachzusammenhang beschreibt $p$ die Wachstumsrate des Flächeninhalts der mit Algen bedeckten Fläche des Sees. Pro Monat nimmt der Inhalt der mit Algen bedeckten Fläche also um ca. $450\,\%$ zu.

2.1

Nullstellen berechnen

$g(t) = 0$ setzen und die Gleichung nach $t$ auflösen:

$\begin{array}[t]{rll} g(t)&=& 0 & \\[5pt] \left(-0,5t^2 +t +2 \right)\cdot \mathrm e^{-0,5\cdot t}&=& 0 & \end{array}$

Da $\mathrm e^{-0,5\cdot t}\neq 0$ für alle $t\in\mathbb{R}$ , folgt mit dem Satz vom Nullprodukt:

$\begin{array}[t]{rll} -0,5t^2+t+2&=& 0 &\quad \scriptsize \mid\; : (-0,5) \\[5pt] t^2 - 2t-4&=& 0 & \end{array}$

$pq$ -Formel anwenden:

$\begin{array}[t]{rll} t_{1/2}&=& -\dfrac{-2}{2}\pm \sqrt{\left(\dfrac{-2}{2}\right)^2 - (-4)} &\\[5pt] &=& 1\pm \sqrt{5} &\\[5pt] t_1&\approx& 3,24 &\\[5pt] t_2&\approx& -1,24 \end{array}$

Da $t\geq 0$ vorgegeben ist, ist die einzige Nullstelle von $g$ im betrachteten Bereich $t_1 \approx 3,24.$

Extremstellen berechnen

1. Schritt: Ableitungen bilden

Mit Produkt- und Kettenregel folgt für die Ableitungen von $g(t)=\left(-0,5t^2 +t +2 \right)\cdot \mathrm e^{-0,5\cdot t}:$

$\(\begin{array}[t]{rll} g$

Die zweite Ableitung wird hier nicht genauer berechnet, da sie nach Aufgabenstellung ohne Herleitung verwendet werden darf.

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

Da $\mathrm e^{-0,5\cdot t}\neq 0$ für alle $t\in\mathbb{R}$ , folgt mit dem Satz vom Nullprodukt:

$\begin{array}[t]{rll} 0,25t^2 -1,5t&=&0 \\[5pt] t\cdot (0,25t-1,5) &=& 0& \\[5pt] \end{array}$

Mit dem Satz des Nullprodukts folgt $t_1=0$ und:

$\begin{array}[t]{rll} 0,25t-1,5 &=& 0&\quad \scriptsize \mid\;+1,5 \\[5pt] 0,25t&=&1,5&\quad \scriptsize \mid\;: 0,25\\[5pt] t_2&=& 6 \end{array}$

3. Schritt: Hinreichendes Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

An der Stelle $t_1 = 0$ befindet sich ein Maximum und an der Stelle $t_2 = 6$ ein Minimum.

2.2

Nullstellen im Sachzusammenhang deuten

Die Funktion $g$ beschreibt die Änderungsrate des Flächeninhalts der mit Algen bedeckten Fläche. Für $g(t)=0$ , ändert sich der Flächeninhalt der mit Algen bedeckten Fläche zum Zeitpunkt $t$ nicht. Dies ist ein notwendiges Kriterium für eine Extremstelle einer Stammfunktion $G$ von $g$ , die den Flächeninhalt der mit Algen bedeckten Fläche zum Zeitpunkt $t$ beschreibt.
Der Flächeninhalt der mit Algen bedeckten Fläche kann hier also sein Maximum bzw. Minimum annehmen.

Bei dem Modell $B$ ist das bei $t=2,34$ der Fall, also nach $2,34$ Monaten. Zu diesem Zeitpunkt könnte der Flächeninhalt sein Maximum bzw. Minimum erreicht haben.

Extremstellen im Sachzusammenhang deuten

Zum Zeitpunkt $t_1 = 0$ nimmt $g$ ein Maximum an. Hier ist die Änderungsrate des Flächeninhalts der mit Algen bedeckten Fläche also am größten, die Algen breiten sich zu diesem Zeitpunkt am schnellsten aus.
Zum Zeitpunkt $t_2 = 6$ nimmt $g$ ein Minimum an. Hier ist die Änderungsrate des Flächeninhalts der mit Algen bedeckten Fläche also am kleinsten, die Algen breiten sich zu diesem Zeitpunkt am langsamsten aus oder reduzieren ihren Bestand sogar.

Nach Modell $B$ breitet sich die Algenart zu Beobachtungsbeginn am schnellsten aus. $6$ Monate nach Beobachtungsbeginn ist das Algenwachstum dagegen am langsamsten.

2.3

Integrationsmethode benennen

Der Funktionsterm von $g$ setzt sich aus zwei Faktoren zusammen. Zur Bestimmung der Stammfunktionen solcher Funktionen wird häufig die partielle Integration verwendet:

$\(\displaystyle\int_{a}^{b}\left(f(x) \cdot g$

Herleitung der Stammfunktion vervollständigen

Anwenden der obigen Formel auf $\left(t^2-2t-4\right)\cdot \mathrm e^{-0,5\cdot t} + \displaystyle\int \left(-2t+2 \right)\cdot \mathrm e^{-0,5\cdot t}\;\mathrm dt$ und Zusammenfassen der einzelnen Summanden liefert:

$\begin{array}[t]{rll} & \left(t^2-2t-4\right)\cdot \mathrm e^{-0,5\cdot t} + \displaystyle\int \left(-2t+2 \right)\cdot \mathrm e^{-0,5\cdot t}\;\mathrm dt \\[5pt] =& \left(t^2-2t-4 \right)\cdot \mathrm e^{-0,5\cdot t}+(-2t +2)\cdot (-2)\cdot \mathrm e^{-0,5\cdot t} - \displaystyle\int(-2)\cdot (-2)\cdot \mathrm e^{-0,5\cdot t}\;\mathrm dt \\[5pt] =& \left(t^2 -2t -4+4t-4 \right)\cdot \mathrm e^{-0,5\cdot t} - \displaystyle\int 4\cdot \mathrm e^{-0,5\cdot t}\;\mathrm dt \\[5pt] =& \left(t^2+2t-8\right)\cdot \mathrm e^{-0,5\cdot t} - 4\cdot(-2)\cdot \mathrm e^{-0,5\cdot t} +C \\[5pt] =& \left(t^2+2t-8 +8 \right)\cdot \mathrm e^{-0,5\cdot t} + C \\[5pt] =& \left(t^2+2t \right)\cdot \mathrm e^{-0,5\cdot t} + C \\[5pt] \end{array}$

Insgesamt gilt also für die Stammfunktionen von $g:$

$G(t) = \left(t^2+2t \right)\cdot \mathrm e^{-0,5\cdot t} + C$

2.4

Bedingungen untersuchen

Zu Modell $B$ ist die Funktion $g$ gegeben, die die Änderungsrate des Inhalts der mit Algen bedeckten Fläche beschreibt. In Aufgabe 2.3 wurde bereits die Gleichung der allgemeinen Stammfunktion $G$ von $g$ bestimmt.

$G$ beschreibt also den Flächeninhalt zum Zeitpunkt $t.$ Nun wird $C$ so gewählt, dass $G$ näherungsweise die Bedingungen aus dem Aufgabentext erfüllt.

Werte aus Aufgabe 1.1 in $G(t)$ einsetzen und nach $C$ auflösen:

$\begin{array}[t]{rll} G(0)&=& 0,1 \\[5pt] \left(0^2+2\cdot 0 \right)\cdot \mathrm e^{-0,5\cdot 0} + C&=& 0,1 \\[5pt] C&=& 0,1 \\[5pt] \end{array}$

Nun ist $G$ gegeben durch $G(t)=(t^2+2\cdot t)\cdot\mathrm e^{-0,5\cdot t} +0,1.$ Es soll auch $G(2)=3$ gelten. Probe:

$\begin{array}[t]{rll} G(2)&=& \left(2^2+2\cdot 2 \right)\cdot \mathrm e^{-0,5\cdot 2} +0,1 \\[5pt] &=& 8\cdot \mathrm e^{-1} + 0,1 \\[5pt] &\approx& 3,04\\[5pt] &\approx& 3 \end{array}$

Mit $C= 0,1$ passt Modell $B$ also näherungsweise zu den im einleitenden Text beschriebenen Werten.

Grenzwert bestimmen

Für den Nenner gilt:

$\begin{array}[t]{rll} \lim\limits_{t\to+\infty} \left(0,1 + 3,4\cdot \mathrm e^{-2,66\cdot t}\right)&=& 0,1+ \lim\limits_{t\to+\infty} \left(3,4\cdot \mathrm e^{-2,66\cdot t}\right) \\[5pt] &=& 0,1+ 3,4\cdot \lim\limits_{t\to+\infty} \left(\left(\mathrm e^{2,66\cdot t}\right)^{-1}\right)\\[5pt] &=& 0,1+ 3,4\cdot \underbrace{\lim\limits_{t\to+\infty} \dfrac{1}{\mathrm e^{2,66\cdot t}}}_{= 0}\\[5pt] &=& 0,1 \\[5pt] \end{array}$

Insgesamt ergibt sich damit:

$\begin{array}[t]{rll} \lim\limits_{t\to+\infty}h(t)&=& \lim\limits_{t\to+\infty}\dfrac{0,35}{0,1 + 3,4\cdot \mathrm e^{-2,66\cdot t}} \\[5pt] &=& \dfrac{0,35}{\lim\limits_{t\to+\infty} \left(0,1 + 3,4\cdot \mathrm e^{-2,66\cdot t}\right)} \\[5pt] &=& \dfrac{0,35}{0,1} \\[5pt] &=& 3,5 \end{array}$

Grenzwert im Sachzusammenhang deuten

Die Funktion $h$ beschreibt im Modell $C$ den Inhalt der mit Algen bedeckten Fläche des Sees. Der Grenzwert beschreibt die Entwicklung auf lange Sicht.

Auf lange Sicht werden nach Modell $C$ ca. $3,5\,\text{a}$ des Sees mit der Algenart bedeckt sein.

Graphen zuordnen

1. Schritt: Alle Funktionsgleichungen zusammenstellen:

$A$ : $f(t) = 0,1\cdot \mathrm e^{1,7\cdot t}$

$B$ : $G(t)= \left(t^2 +2t \right)\cdot \mathrm e^{-0,5\cdot t} +0,1$

$C$ : $h(t)= \dfrac{0,35}{0,1+ 3,4\cdot \mathrm e^{-2,66\cdot t}}$

2. Schritt: Graphen zuordnen

Die drei Graphen unterscheiden sich in den Grenzwerten für $t \to +\infty$ .
Für $h(t)$ ist dieser gegeben als $\lim\limits_{t\to+\infty} h(t) = 3,5.$

Der zur Funktion $h$ und damit zum Modell $C$ gehörige Graph ist daher $\text{(II)}$ .

Für $f$ und $G$ ergibt sich:

$\begin{array}[t]{rll} \lim\limits_{t\to+\infty}f(t)&=& \lim\limits_{t\to+\infty}\left(0,1\cdot \mathrm e^{1,7\cdot t} \right) \\[5pt] &=& +\infty \\[10pt] \lim\limits_{t\to+\infty}G(t)&=&\lim\limits_{t\to+\infty}\left( \left(t^2 +2t \right)\cdot \mathrm e^{-0,5\cdot t} + 0,1 \right)\\[5pt] &=& 0,1 + \lim\limits_{t\to+\infty}\left( \underbrace{\left(t^2 +2t \right)}_{\to +\infty}\cdot \underbrace{\mathrm e^{-0,5\cdot t}}_{\to 0}\right) \\[5pt] &=& 0,1 \end{array}$

Somit folgt mithilfe von Material 2, dass Graph $\text{(III)}$ zu $f,$ also Modell $A,$ gehört und Graph $\text{(I)}$ zu $G$ bzw. Modell $B.$

Eignung erörtern

Im Modell $A$ würde sich die Algenart unbegrenzt ausbreiten. Der See hat allerdings eine begrenzte Größe, so dass sich die Algen nicht unendlich weit ausbreiten können. Modell $A$ ist daher nur bis zu einem gewissen Punkt realistisch, auf lange Sicht aber nicht.

Im Modell $B$ würde der Flächeninhalt der mit Algen bedeckten Fläche bis zu einem Wert von ca. $3,5\,\text{a}$ ansteigen und dann bis zu einem Wert von ca. $0,1 \text{a}$ abnehmen. Dies könnte zum Beispiel durch den erhöhten Nährstoffverbrauch bei einem großen Bestand oder beispielsweise niedrigeres Nährstoffangebot im Winter erklärt werden, wodurch sich die Fläche verringert.
Modell $B$ kann also durchaus realistisch sein.

In Modell $C$ steigt der Flächeninhalt bis zu einem Wert von ca. $3,5\,\text{a}$ und bleibt dann näherungsweise bei diesem. Das könnte einerseits an der begrenzten Fläche des Sees oder auch an dem begrenzten Nahrungsangebot liegen, das eventuell für in etwa diesen Bestand auf Dauer ausreicht.
Somit könnte auch Modell $C$ realistisch sein.