C – Lineare Algebra / Analytische Geometrie

Ein Forscherteam erkundet mit Hilfe von ferngesteuerten Unterwasser-Drohnen die Unterwasserwelt und insbesondere Delfine. Die Unterwasser-Drohnen werden im Modell als punktförmig angenommen und ihre Bewegungen sind als stückweise geradlinig anzusehen. Die Meeresoberfläche liegt in der $x$ - $y$ -Ebene. Eine Koordinateneinheit entspricht einem Meter.

Die Drohnen $D_1$ und $D_2$ befinden sich zu Beobachtungsbeginn in den Punkten $A(0\mid0\mid-100)$ und $B(40\mid50\mid-90)$ auf dem geneigten, ebenen Meeresgrund. Im Modell liegt der Meeresgrund in der durch die Koordinatengleichung $E: x+y-9 z=900$ beschriebenen Ebene.

1.1

Bestimme den Abstand der beiden Drohnen zueinander.

(2 BE)

1.2

Berechne den Winkel, unter dem der Meeresgrund die Meeresoberfläche (an der Küste) schneidet.

(3 BE)

Die Drohne $D_1$ bewegt sich nach Beobachtungsbeginn vom Punkt $A(0\mid0\mid-100)$ aus pro Sekunde um den Vektor $\pmatrix{0\\0,5\\1}$ in Richtung der Meeresoberfläche. Die Drohne $D_2$ bewegt sich nach Beobachtungsbeginn mit konstanter Geschwindigkeit und benötigt $10$ Sekunden, um vom Punkt $B(40\mid50\mid-90)$ zum Punkt $T(35\mid55\mid-80)$ zu gelangen.

2.1

Ermittle den Punkt $P,$ in dem die Drohne $D_2$ die Meeresoberfläche erreicht, wenn sie sich ohne Richtungsänderung weiterbewegt.

(3 BE)

2.2

Erkläre den Ansatz in Zeile $(1)$ im Sachzusammenhang und leite die Gleichung in Zeile $(2)$ rechnerisch her. Deute das Ergebnis in Zeile $(3)$ im Sachzusammenhang.

$(1)$

Zeile $(1)$ anzeigen

$(2)$

$d(t)=\sqrt{0,25 t^2-40t+4200}$

$(3)$

$\(d$ $d(80) \approx 51$

(6 BE)

Delfine sind soziale Tiere, die in Gruppen zusammenleben. Die Mitgliedschaft in den Gruppen ist nicht fest, Wechsel kommen häufig vor. Mit Hilfe von Unterwasser-Drohnen wird das monatliche Wechselverhalten einer aus den drei Gruppen $A, B,$ und $C$ bestehenden Delfinpopulation beobachtet. Zu Beobachtungsbeginn befinden sich $50\,\%$ der Delfine in Gruppe $A,\;20\,\%$ in Gruppe $B$ und $30\,\%$ in Gruppe $C.$ In der Abbildung ist der bereits vor Beobachtungsbeginn gültige Übergangsgraph für das monatliche Wechselverhalten angegeben.

Übergangsgraph

3.1

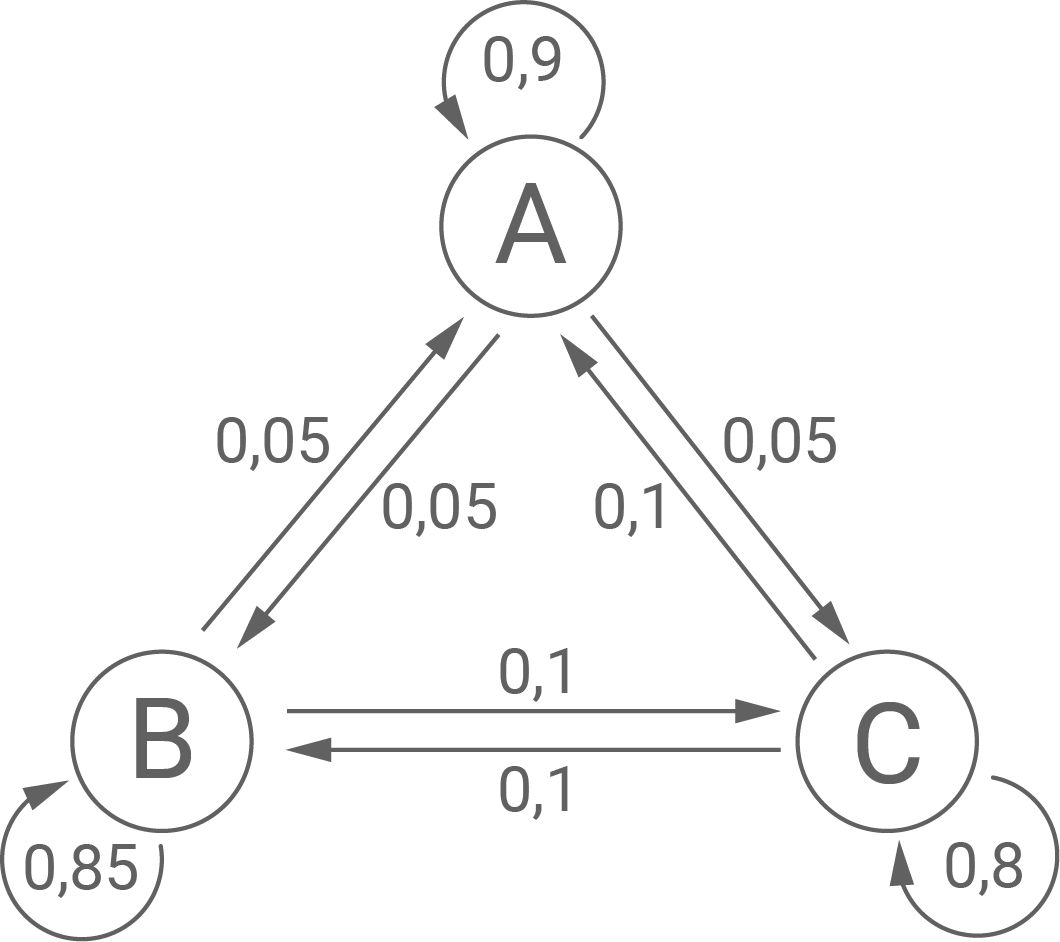
Bestimme die prozentuale Verteilung der Delfine auf die drei Gruppen $A, B$ und $C$ einen Monat nach Beobachtungsbeginn. Gib einen Ansatz an, mit dem der Vektor $\overrightarrow{v}=\pmatrix{a\\b\\c}$ ermittelt werden kann, der die Verteilung der Delfine auf die drei Gruppen $A, B$ und $C$ einen Monat vor Beobachtungsbeginn beschreibt.

(4 BE)

3.2

Die zur Abbildung gehörige Übergangsmatrix werde mit $M$ bezeichnet.
Es gilt: $\lim\limits_{n\to+\infty} M^n \cdot\pmatrix{0,5\\0,2\\0,3}\approx\pmatrix{0,42\\0,32\\0,26}$
Deute diesen Grenzwert im Sachzusammenhang.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$\begin{array}[t]{rlll} \left\vert\overrightarrow{AB}\right\vert&=&\left\vert\pmatrix{40\\50\\-90}-\pmatrix{0\\0\\-100}\right\vert \\[5pt] &=&\left\vert\pmatrix{40\\50\\10}\right\vert \\[5pt] &=&\sqrt{40^2+50^2+10^2} \\[5pt] &\approx&64,81 \end{array}$

Der Abstand der beiden Drohen beträgt somit zu Beginn ca. $64,81\;\text{m}.$

1.2

Der Normalenvektor der Ebene, die den Meeresgrund beschreibt, ergibt sich mit Hilfe der Ebenengleichung wie folgt:

$\overrightarrow{n}=\pmatrix{1\\1\\-9}$

Zusammen mit dem Normalenvektor der $x$ - $y$ -Ebene folgt somit für den gesuchten Winkel:

Rechenweg anzeigen

$\alpha \approx 8,93^\circ$

2.1

Für den Richtungsvektor der Geraden $g,$ entlang derer sich die Drohne $D_2$ bewegt, folgt:

$\pmatrix{35\\55\\-80}-\pmatrix{40\\50\\-90}=\pmatrix{-5\\5\\10}$

Für die Geradengleichung von $g$ gilt somit:

$g:\overrightarrow{x}=\pmatrix{40\\50\\-90}+s\cdot\pmatrix{-5\\5\\10}$

Da die Meeresoberfläche durch die $x$ - $y$ -Ebene beschrieben wird, erreicht $D_2$ diese, wenn $-90+10s=0$ gilt. Für $s$ ergibt sich damit:

$\begin{array}[t]{rlll} -90+10s&=&0 &\mid\;+90 \\[5pt] 10s&=&90 &\mid\;:10 \\[5pt] s&=&10 \end{array}$

Einsetzen in die Geradengleichung ergibt:

$\begin{array}[t]{rlll} \overrightarrow{OP}&=&\pmatrix{40\\50\\-90}+9\cdot\pmatrix{-5\\5\\10} \\[5pt] &=&\pmatrix{-5\\95\\0} \end{array}$

Die Koordinaten des gesuchten Punkts sind somit durch $P(-5\mid95\mid0)$ gegeben.

2.2

Ansatz in Zeile $(1)$ im Sachzusammenhang erklären

Die Funktion $d(t)$ gibt den Abstand der beiden Drohnen $t$ Sekunden nach Beobachtungsbeginn an.

Gleichung in Zeile $(1)$ rechnerisch herleiten

Mit Zeile $(1)$ folgt:

Rechenweg anzeigen

$d(t) = \sqrt{0,25t^2-40t+4200}$

Ergebnis in Zeile $(1)$ im Sachzusammenhang deuten

Der Abstand der Drohnen wird $80$ Sekunden nach Beobachtungsbeginn minimal und beträgt zu diesem Zeitpunkt ungefähr $51\;\text{m}.$

3.1

Prozentuale Verteilung bestimmen

Aus der Abbildung folgt für die Übergangsmatrix:

$\pmatrix{0,9 & 0,05 & 0,1\\0,05 & 0,85 & 0,1\\0,05 & 0,1 & 0,8}$

Damit ergibt sich:

Rechenweg anzeigen

$\pmatrix{0,9 & 0,05 & 0,1\\0,05 & 0,85 & 0,1\\0,05 & 0,1 & 0,8}\cdot\pmatrix{0,5\\0,2\\0,3}$ $= \pmatrix{0,49\\0,225\\0,285}$

Einen Monat nach Beobachtungsbeginn befinden sich somit $49\,\%$ der Delfine in Gruppe $A,$ $22,5\,\%$ in Gruppe $B$ und $28,5\,\%$ ind Gruppe $C.$

Ansatz angeben

Multiplizieren der Anfangsverteilung mit der Inversen der Übergangsmatrix liefert die Verteilung einen Monat vor Beobachtungsbeginn. Ein möglicher Ansatz ist somit wie folgt gegeben:

$\pmatrix{a\\b\\c}=\pmatrix{0,9 & 0,05 & 0,1\\0,05 & 0,85 & 0,1\\0,05 & 0,1 & 0,8}^{-1}\cdot\pmatrix{0,5\\0,2\\0,3}$

3.2

Auf lange Sicht entsteht ein stabiler Zustand, bei dem ungefähr $42\,\%$ der Delfine in Gruppe $A$ sind, $32\,\%$ in Gruppe $B$ und $26\,\%$ in Gruppe $C.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?