A1 - Analysis

Gegeben ist die Funktionenschar $f_k$ mit $f_{k}(x)=\dfrac{x+k}{\mathrm e^{x}}, \; x\in\mathbb{R},\; k\in\mathbb{R}$ .

Abildung 1 enthält Graphen von Funktionen der Schar.

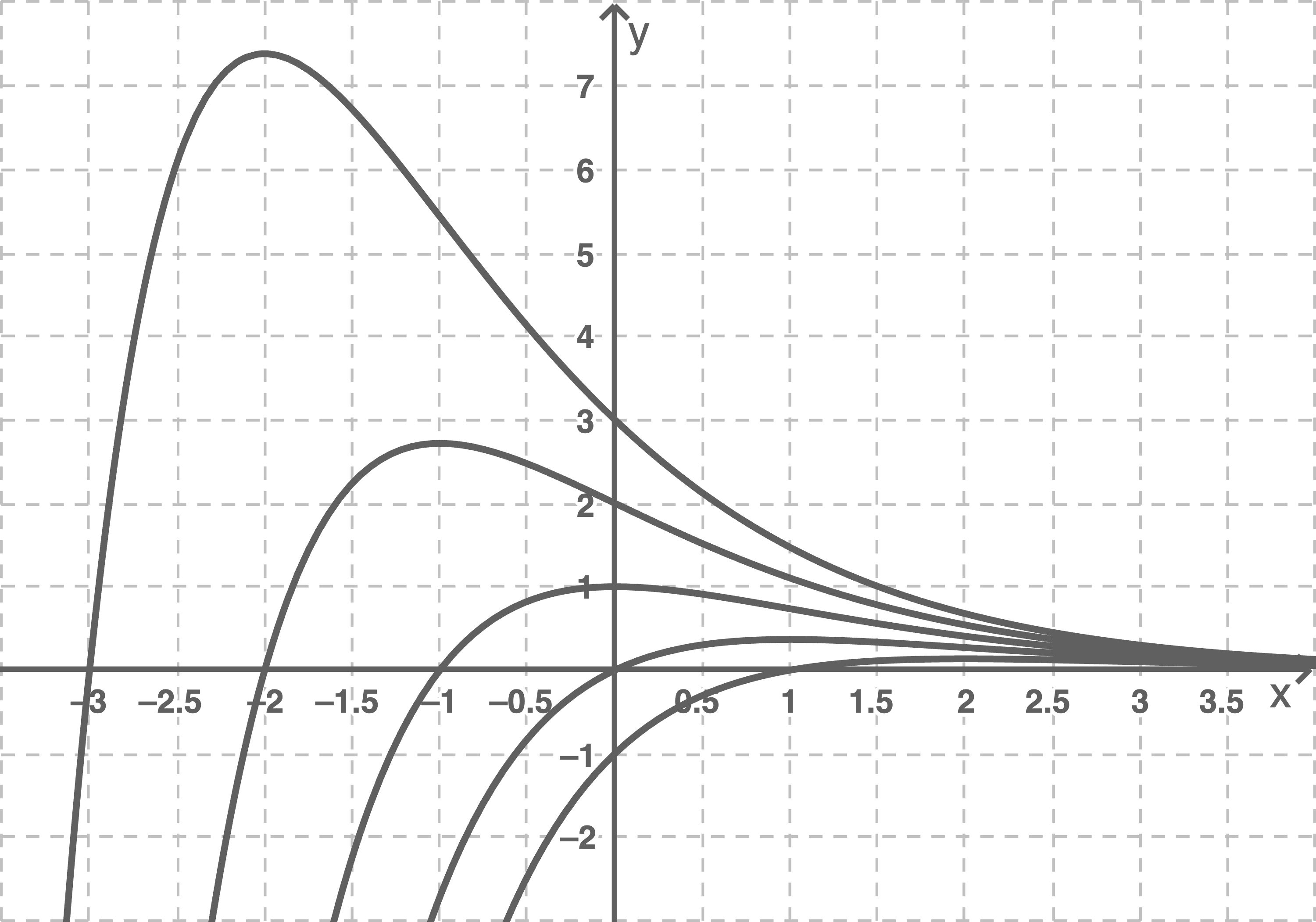
Abbildung 1

1.1

Berechne die Nullstellen der Scharfunktionen.

Gib für die Graphen in Abbildung 1 die zugehörigen ganzzahligen Parameterwerte von $k$ an.

(4 BE)

1.2

Berechne jeweils nur anhand der notwendigen Bedingung die Extrem- und Wendestellen der Schar und zeige, dass für alle Funktionen der Schar die Extremstelle stets genau in der Mitte von Null- und Wendestelle liegt.

(5 BE)

1.3

Skizziere in Abbildung 1 die Kurve, die die Hochpunkte verbindet, und leite für die Ortskurve der Hochpunkte die zugehörige Funktionsgleichung her.

(4 BE)

1.4

Zeige, dass für jede Scharfunktion $f_k$ die 2. Ableitungsfunktion $\(f_{k}$ ebenfalls eine Funktion der Schar ist.

Ermittle, durch welche Abbildungen der Graph von $\(f_{k}$ aus dem Graphen von $f_k$ hervorgeht.

(4 BE)

2.1

Berechne mit Hilfe partieller Integration (Produktintegration) eine Stammfunktionenschar $F_k$ von $f_k.$

$\big[$ zur Kontrolle: $\; F_{k}(x)$ $=-(x+k+1)$ $\cdot\mathrm e^{-x} \big]$

(5 BE)

2.2

Untersuche rechnerisch, ob die Graphen der Schar mit der $x$ -Achse eine Fläche einschließen, die einen endlichen Inhalt hat, und gib diesen gegebenenfalls an.

(6 BE)

Aus der Funktionenschar $f_k$ entsteht durch geeignete Verschiebung jedes Graphen parallel zur $x$ -Achse eine neue Funktionenschar $g_k,$ deren Graphen alle durch den Ursprung gehen (Abbildung 2).

Zeige, dass sich der Term für $g_k$ als $g_{k}(x)=x\cdot\mathrm e^{k-x}$ schreiben lässt.

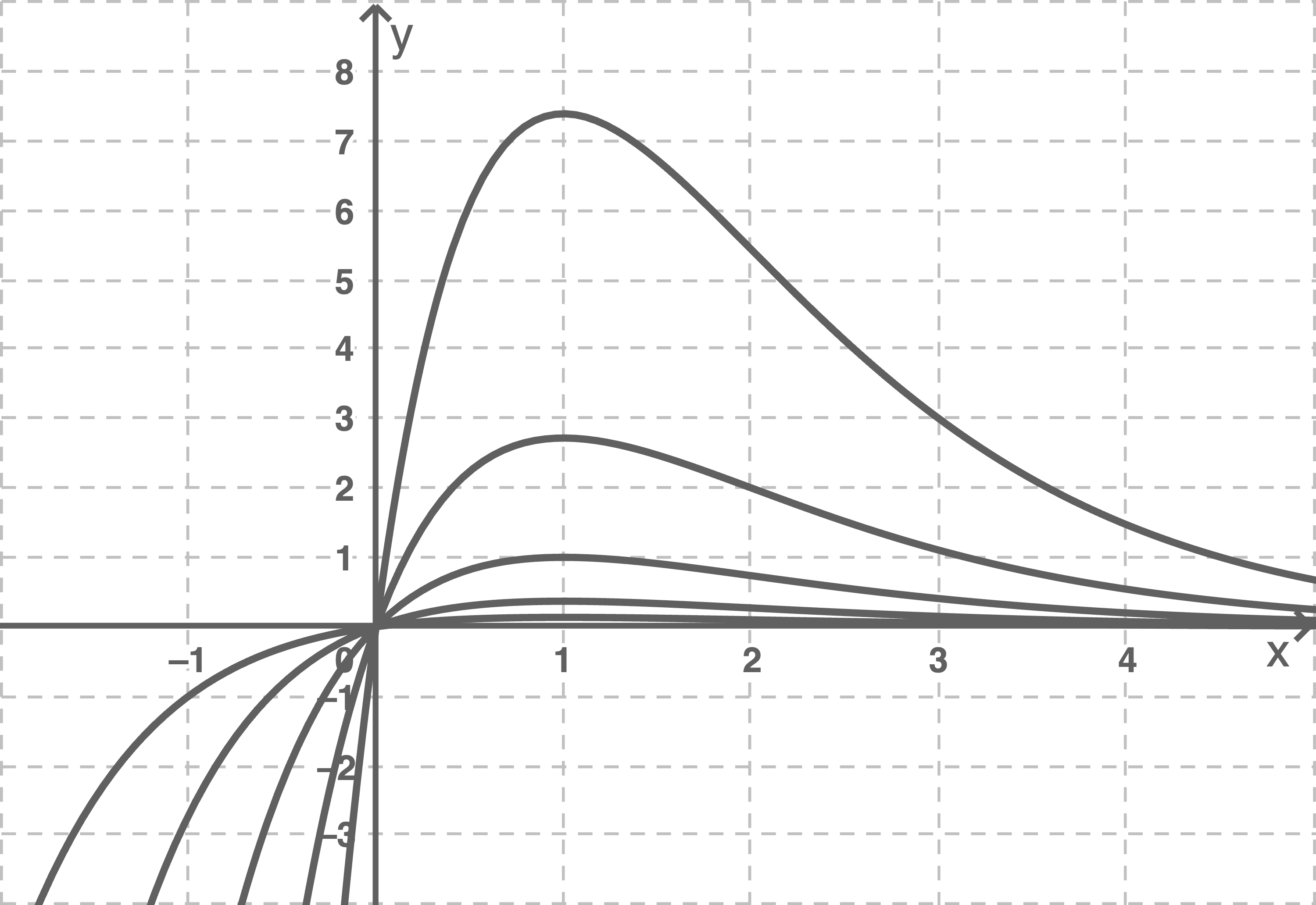
Abbildung 2

(4 BE)

Gewisse Wachstumsprozesse lassen sich durch Graphen wie in Abbildung 2 beschreiben.

In Abbildung 3 ist die Gewichtszunahme von jungen Hunden graphisch dargestellt. Die zugrunde liegenden Daten lassen sich durch abgeänderte Funktionen der Funktionenschar $g_k$ (vgl. Aufgabe 3) gut approximieren.

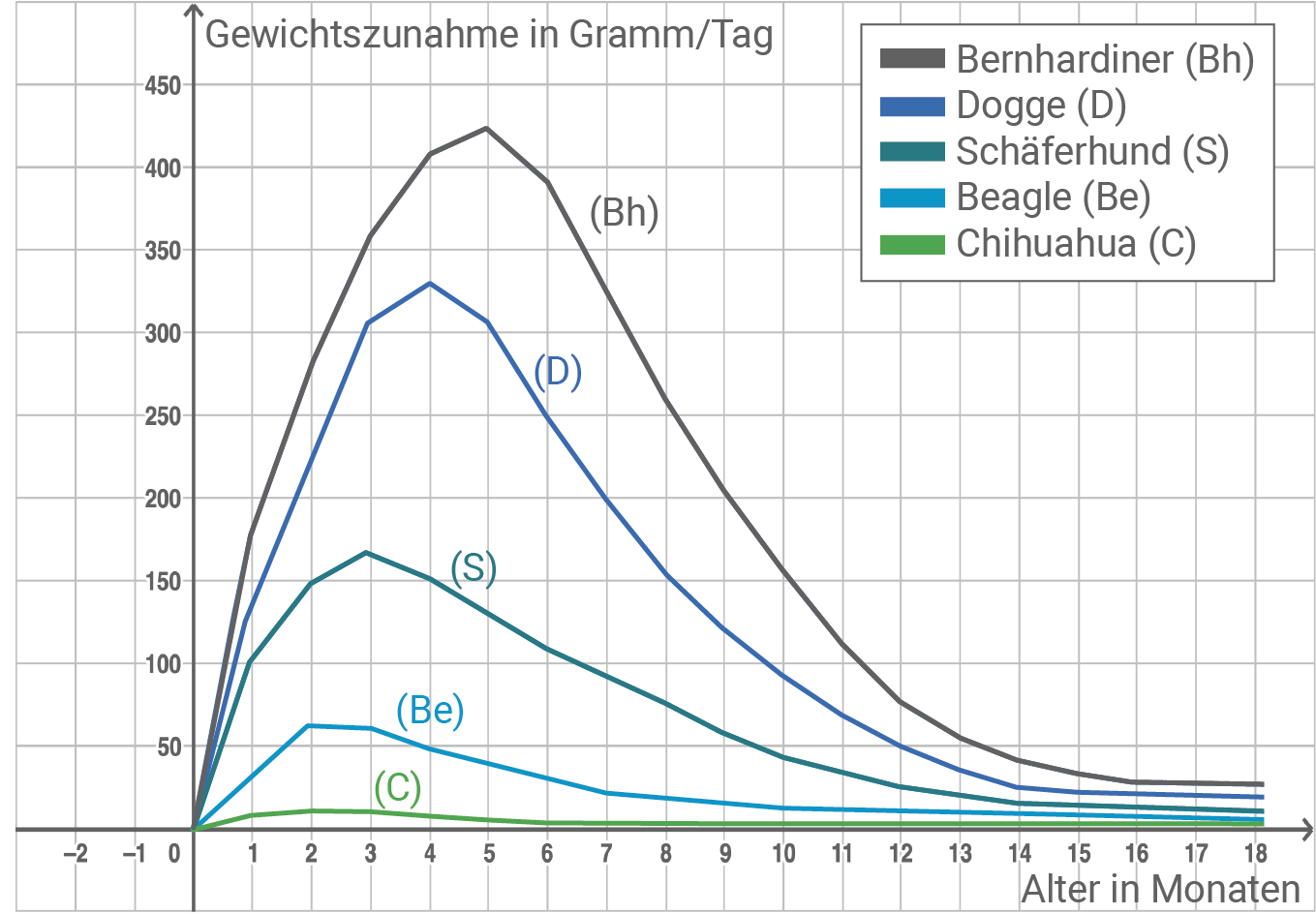
Hundegewicht Zunahme Hessen Mathe Abi 2014

Abbildung 3

Für den Schäferhund können dem Diagramm folgende Werte entnommen werden:

Alter (in Monaten)	Gewichtszunahme (in g/Tag)
1	100
2	150
3	165
5	130
7	95
10	45
13	20

4.1

Beschreibe die in den Graphen von Abbildung 3 enthaltenen Aussagen im Sachzusammenhang. Auf Unterschiede zwischen den einzelnen Graphen soll nicht eingegangen werden.

(2 BE)

4.2

Leite eine abgeänderte Funktion aus der Schar $g_k$ her, die das Wachstum der Schäferhunde annähernd beschreibt und deren Graph den gleichen Hochpunkt wie der Graph $S$ in Abbildung 3 hat.

Hinweis: Denk an eine Streckung oder Stauchung eines Graphen der Schar.

(6 BE)

1.1

Nullstellen berechnen

Es gilt:

$\begin{array}[t]{rll} f_k(x)&=& 0 &\\[5pt] \frac{x+k}{\mathrm e^x}&=& 0 &\quad \scriptsize \mid\; \cdot \mathrm e^x \\[5pt] x+k&=& 0& \quad \scriptsize \mid\; -k\\[5pt] x&=& -k \end{array}$

Die Nullstellen der Scharfunktionen $f_k$ sind somit gegeben durch $x_N=-k.$

Parameterwerte angeben

Die Graphen von $f_k$ besitzen jeweils eine Nullstelle bei $x_N=-k.$ Die in der Abbildung gegebenen Graphen besitzen die Nullstellen $x_N = -3$ , $-2$ , $-1$ , $0$ und $1.$

Somit folgen die Parameterwerte der Graphen mit $k = 3, 2, 1, 0$ und $-1.$

1.2

1. Schritt: Ableitungen bilden

Mit der Quotientenregel folgt:

$\(\begin{array}[t]{rll} f_k$

$\begin{array}[t]{rll} f_k‘‘(x)&=&\dfrac{-1\cdot\mathrm e^x-(1-x-k)\cdot \mathrm e^x}{(\mathrm e^x)^2} &\quad \scriptsize \\[5pt] &=&\dfrac{(-1-1+x+k)\cdot\mathrm e^x}{\mathrm e^{2x}} &\quad \scriptsize \\[5pt] &=&\dfrac{-2+x+k}{\mathrm e^x} \end{array}$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Da nur die Anwendung der notwendigen Bedingung gefordert ist, folgen die Extremstellen der Schar mit $x_E=1-k.$

3. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} f_k$

Da nur die Anwendung der notwendigen Bedingung gefordert ist, folgen die Wendestellen der Schar mit $x_W=2-k.$

4. Schritt: Lage der Extremstelle nachweisen

Für die Mitte $x_M$ zwischen der Nullstelle $x_N=-k$ und der Wendestelle $x_W = 2-k$ gilt:

$\begin{array}[t]{rll} x_M&=& \dfrac{1}{2}\cdot (x_N +x_W)& \\[5pt] &=&\dfrac{1}{2}\cdot(-k+2-k) &\quad \scriptsize \\[5pt] &=&1-k &\quad \scriptsize \\[5pt] &=&x_E \end{array}$

Somit liegt die Extremstelle jeder Scharfunktion genau in der Mitte von Null- und Wendestelle.

1.3

Kurve skizzieren

Die Parameter der gegebenen Graphen sind $k = 3,2,1,0$ und $-1.$

Der Extrempunkt jeder Scharfunktion liegt an der Stelle $x_E=1-k.$ Die Extremstellen der Graphen folgen also mit $x_E = -2,-1,0,1$ und $2.$

Durch Eintragen der Hochpunkte in Abbildung 1 lässt sich die Ortskurve wie folgt skizzieren:

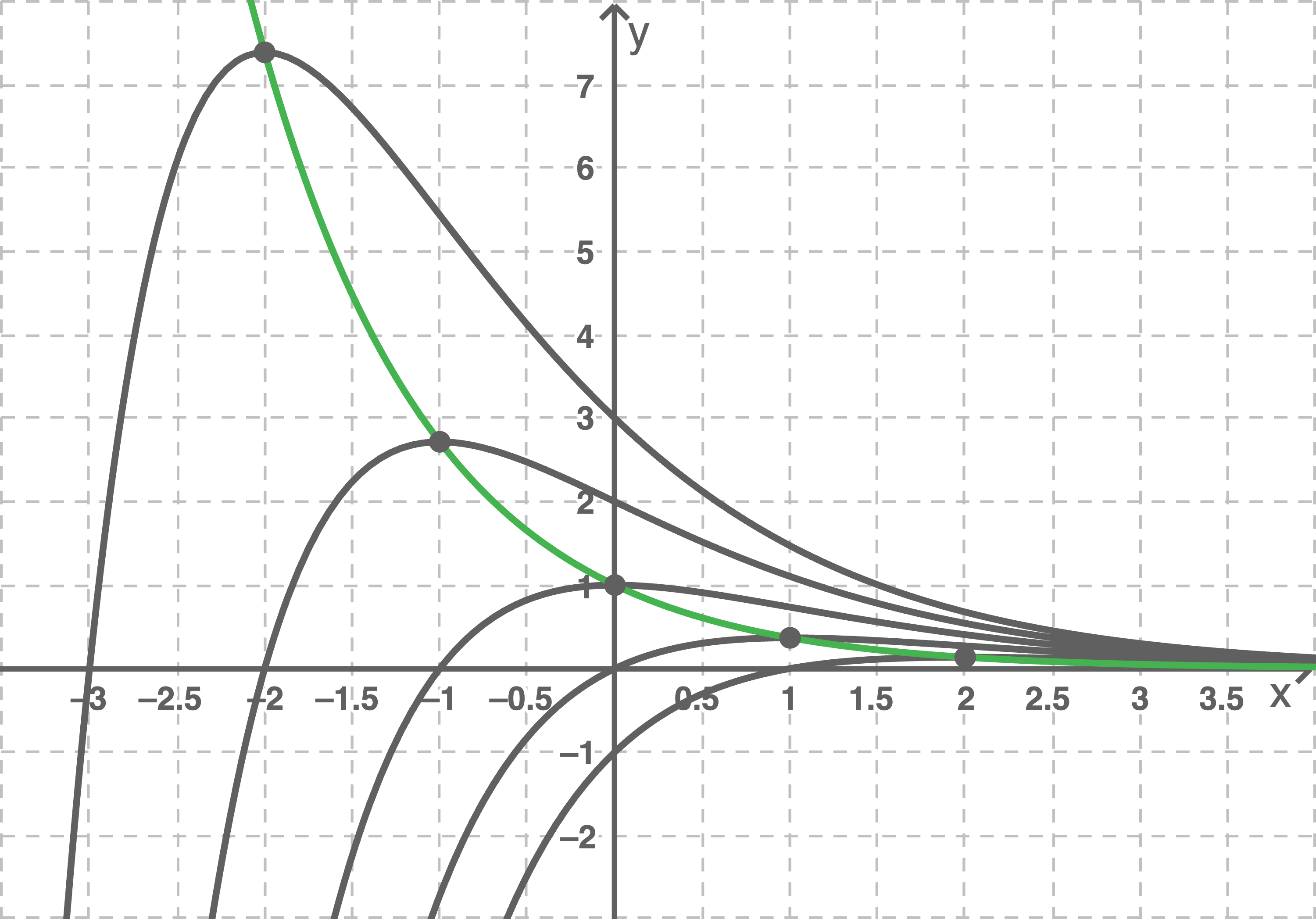Loesung Funktionenschar Ortskurve Extremstellen Hessen 2014

Funktionsgleichung herleiten

Es gilt:

$\begin{array}[t]{rll} x_E&=& 1-k &\quad \scriptsize \mid\;+k \quad \scriptsize \mid -x_E \\[5pt] k&=& 1-x_E \end{array}$

Einsetzen der Extremstelle $x_E= 1-k$ in die Funktionsgleichung von $f_k$ liefert die $y$ -Koordinate der Extrempunkte in Abhängigkeit von $k:$

$\begin{array}[t]{rll} y_E&=&f_k(1-k) &\quad \scriptsize \\[5pt] &=&\dfrac{1-k+k}{\mathrm e^{1-k}} &\quad \scriptsize \\[5pt] &=&\dfrac{1}{\mathrm e^{1-k}} \end{array}$

Einsetzen von $k=1-x_E$ liefert nun:

$\begin{array}[t]{rll} y_E&=&\dfrac{1}{\mathrm e^{1-k}} &\quad \scriptsize \\[5pt] &=&\dfrac{1}{\mathrm e^{1-(1-x_E)}} &\quad \scriptsize \\[5pt] &=&\dfrac{1}{\mathrm e^{x}} \end{array}$

Damit ist die Funktionsgleichung der Ortskurve der Hochpunkte von $f_k$ gegeben durch $y= \dfrac{1}{\mathrm e^x}.$

1.4

Zweite Ableitungsfunktion prüfen

Für jede Scharfunktion muss es ein $k_0$ geben, sodass gilt:

$\(\begin{array}[t]{rll} f_k$

Damit ist $\(f_k$ mit $k_0 = k-2.$

Folglich ist $\( f_k$ für jedes $k$ ebenfalls eine Funktion der Schar $f_k.$

Abbildungen ermitteln

Aus Abbildung 1 kann abgelesen werden, dass der Graph von $f_{-1}$ durch Verschiebung um zwei Einheiten in positive $x$ -Richtung und einer leichten Streckung aus dem Graphen von $f_1$ hervorgeht.

Für den genauen Streckungsfaktor wird der Funktionsterm von $\(f_k$ in eine Darstellungsweise in Abhängigkeit von $f_k$ gebracht. Dafür wird der Bruch mit $1=\dfrac{\mathrm e^{-2}}{\mathrm e^{-2}}$ erweitert:

$\(\begin{array}[t]{rll} f_k$

Der Graph von $\(f_k$ geht also durch eine Verschiebung um zwei Einheiten in positive $x$ -Richtung und durch eine Streckung um den Faktor $\mathrm e^{-2}$ aus dem Graphen von $f_k$ hervor.

2.1

Für die partielle Integration (Produktintegration) gilt:

$\( \displaystyle\int_{}^{}u(x)\cdot v$

Vollständige Gleichung anzeigen

Es ist gegeben:

$\(\begin{array}[t]{rll} f_k(x)&=& \dfrac{x+k}{\mathrm e^x}& \\[5pt] &=& (x+k)\cdot \mathrm e^{-x}& \\[5pt] &=& u(x)\cdot v$

Somit folgt:

$u(x)=x+k$

$\(u$

$v(x)=-\mathrm e^{-x}$

$\(v$

Eine Stammfunktionenschar $F_k$ von $f_k$ ergibt sich also mit:

$\displaystyle\int_{}^{}(x+k)\cdot \mathrm e^{-x}\mathrm dx=...$

Vollständige Rechnung anzeigen

Eine Stammfunktionenschar der Funktionenschar $f_k$ lautet folglich $F_k(x) = -(x+k+1)\cdot\mathrm e^{-x}.$

2.2

Da die Nullstelle bereits durch $a=-k$ gegeben ist, gilt für den Flächeninhalt zwischen den Graphen der Schar und der $x$ -Achse:

$\lim\limits_{b\to\infty} \displaystyle\int_{-k}^{b}f_k(x)\,\mathrm dx=...$

Vollständige Rechnung anzeigen

Da der exponentiellen Term $\mathrm e^{-b}$ stärker wächst als der lineare Term $-(b+k+1),$ strebt der gesamte Term $-(b+k+1)\cdot\mathrm e^{-b}$ für $b\rightarrow\infty$ folglich gegen 0.

Damit ergibt sich:

$\lim\limits_{b\to\infty} \displaystyle\int_{-k}^{b}f_k(x)\,\mathrm dx= \mathrm e^k$

Rechenweg anzeigen

Die Graphen der Schar $f_k$ schließen mit der $x$ -Achse also eine Fläche mit endlichem Inhalt ein. Dieser beträgt $\mathrm e^k$ Flächeneinheiten.

Da die Nullstellen der Funktionsschar jeweils an der Stelle $x_N=-k$ liegen, muss jeder Graph um $k$ Einheiten nach rechts verschoben werden.

Somit ergibt sich:

$\begin{array}[t]{rll} g_k(x)&=& f_k(x-k) & \\[5pt] &=& \dfrac{x-k+k}{\mathrm e^{x-k}} & \\[5pt] &=& \dfrac{x}{\mathrm e^{x-k}} & \\[5pt] &=& x\cdot\mathrm e^{-(x-k)} & \\[5pt] &=& x\cdot\mathrm e^{k-x} \end{array}$

Der Term für $g_k$ lässt sich somit als $g_k(x)= x\cdot\mathrm e^{k-x}$ schreiben.

4.1

Alle Graphen wachsen zunächst sehr stark, bis sie ihren Hochpunkt erreicht haben. In den ersten Monaten legen die Welpen also immer schneller an Gewicht zu, bis sie spätestens im 5. Lebensmonat die höchste Gewichtszunahme erreichen.

Die Graphen fallen dann wieder ab, allerdings langsamer, als sie zuvor gestiegen sind. Die Gewichtszunahme nimmt also immer weiter ab.

Zum Schluss nähern sich alle Graphen asymptotisch der $x$ -Achse an. Nach ca. 12 bis 18 Monaten hat sich die Gewichtszunahme also weitestgehend dem Wert Null angenähert, sodass die Hunde etwa ihr Endgewicht erreicht haben.

4.2

Der Graph der Funktion $w(t)$ , die das Wachstum der Schäferhunde annähernd beschreiben soll, soll den gleichen Hochpunkt besitzen wie der Graph $S.$ Dieser ist gegeben durch $H(3\mid 165).$

1. Schritt: Ableitung bilden

Mit der Produktregel ergibt sich:

$\(\begin{array}[t]{rll} g$

2. Schritt: Koordinaten der Hochpunkte bestimmen

Anwenden der notwendigen Bedingung für Extremstellen:

$\begin{array}[t]{rll} 0&=& (1-x_G)\cdot\mathrm e^{k-x_G} &\quad \scriptsize \mid\; : \mathrm e^{k-x_G}\\[5pt] 0&=& 1-x_G &\quad \scriptsize \mid\; +x_G\\[5pt] x_G&=& 1 \end{array}$

Da aus dem Verlauf der Graphen hervorgeht, dass genau eine Extremstelle existiert, kann auf die Anwendung der hinreichenden Bedingung verzichtet werden.

$y$ -Koordinate berechnen:

$g_k(1)=1\cdot\mathrm e^{k-1}=\mathrm e^{k-1}$

Die Koordinaten der Hochpunkte der Graphen von $g_k$ sind somit gegeben durch $G(1\mid \mathrm e^{k-1}).$

3. Schritt: Wert von $\boldsymbol{k}$ ermitteln

Da der Graph von $w(t)$ ebenso wie der Graph $S$ den Hochpunkt $H(3\mid 165)$ besitzen soll, muss gelten:

$\begin{array}[t]{rll} 165&=&\mathrm e^{k-1} &\quad \scriptsize \mid\; \ln \\[5pt] \ln(165)&=& k-1 &\quad \scriptsize \mid\;+1 \\[5pt] \ln(165)+1&=& k & \\[5pt] 6,11&\approx& k \end{array}$

4. Schritt: Sreckungsfaktor bestimmen

Damit der Hochpunkt des Graphen von $w(t)$ statt bei $x =1$ an der Stelle $x = 3$ liegt, muss der Graph von $g_{6,11}$ entsprechend in $x$ -Richtung gestreckt werden.

Es soll gelten:

$w(3) = g_{6,11}(1)$

Der Streckungsfaktor entlang der $x$ -Achse folgt also mit $\dfrac{1}{3}.$

Eine abgeänderte Funktion der Schar $g_k,$ die das Wachstum der Schäferhunde annähernd beschreibt und deren Graph den gleichen Hochpunkt wie der Graph $S$ in Abbildung 3 hat, ist somit gegeben durch :

$\begin{array}[t]{rll} w(t)&=& g_{6,11}\left(\frac{1}{3}\cdot x\right)& \\[5pt] &=& \frac{1}{3}\cdot x\cdot\mathrm e^{6,11-\frac{1}{3}\cdot x} \end{array}$