A2 - Analysis
Gegeben ist die Funktionenschar 
mit 
Die Graphen aller Funktionen dieser Schar haben an der Stelle 
einen Hochpunkt.
mit Die Graphen aller Funktionen dieser Schar haben an der Stelle einen Hochpunkt.
1.1
Bestätige durch eine Rechnung, dass für jede Funktion der Schar eine Extremstelle ist.
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
eine Extremstelle ist.
Hinweis: Die Untersuchung der notwendigen Bedingung ist ausreichend.
(6 BE)
1.2
Berechne, für welchen Wert des Parameters 
der Graph der zugehörigen Funktion der Schar durch den Punkt 
verläuft.
der Graph der zugehörigen Funktion der Schar durch den Punkt verläuft.
(4 BE)
2.
Bestimme die Asymptote der Graphen von für 
.
für .
(3 BE)
3.
Zeige durch partielle Integration, dass
eine Stammfunktion von 
ist.
ist.
(8 BE)
4.
Alle Funktionen der Schar haben genau eine Nullstelle. Zeige unter Verwendung einer Rechnung, dass alle Funktionen der Schar die gleiche Nullstelle haben.
Hinweis: Die Nullstelle muss nicht ermittelt werden.
Hinweis: Die Nullstelle muss nicht ermittelt werden.
(4 BE)
5.
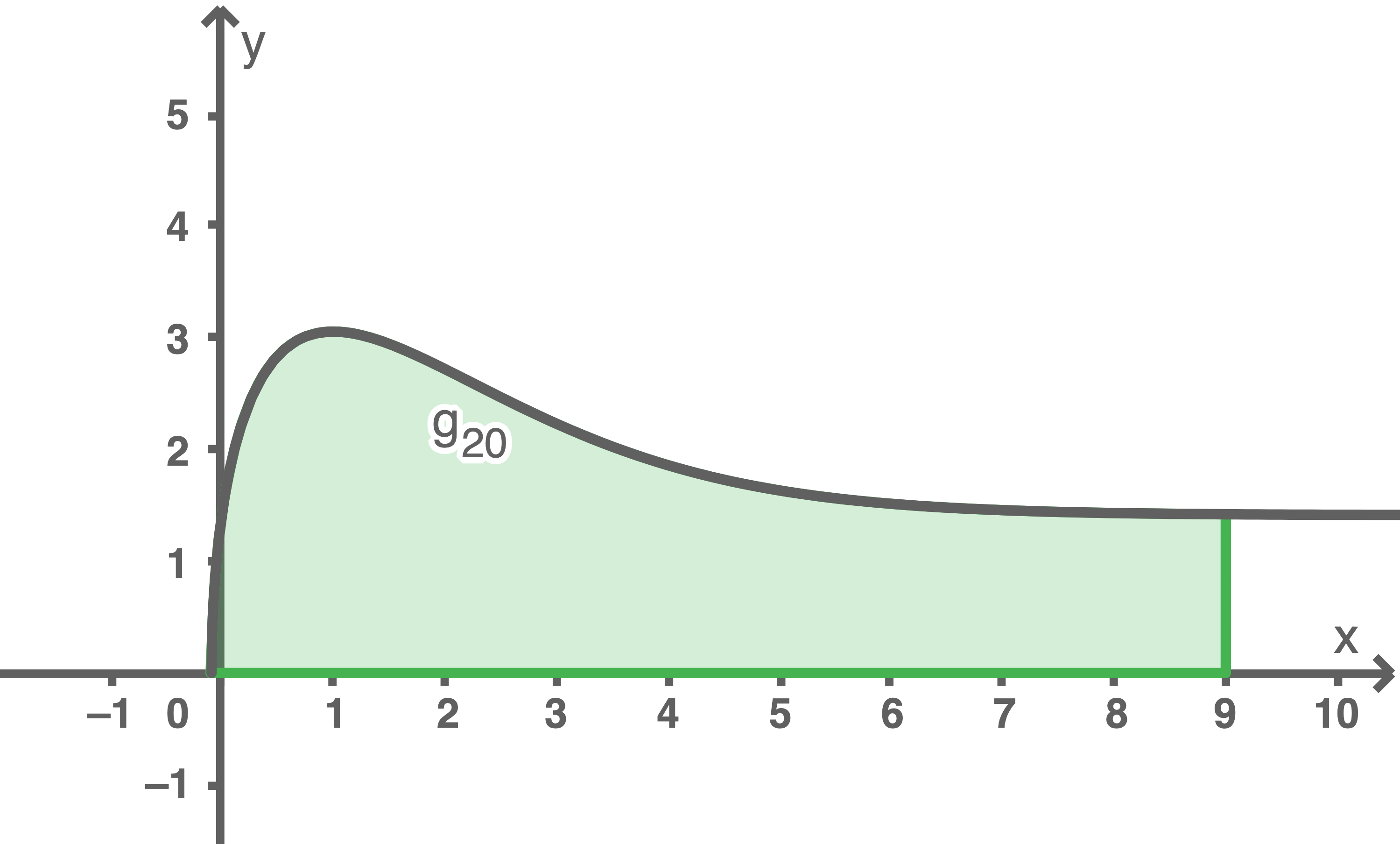
Eine Firma möchte ein neues Likörglas ähnlich wie das in Material 1 dargestellte produzieren. Es soll einen massiven Stiel erhalten. In Material 2 ist die obere Hälfte der Querschnittsfläche des um 
nach rechts gekippten Glases (ohne Stiel) abgebildet (
entspricht 
). Durch Rotation des Graphen von 
um die 
-Achse im Intervall ![\(I= \left[-0,09; 9\right]\)](https://www.schullv.de/resources/formulas/d1ed905e413b6aa1fddeec7cd135aa224f1b7e289417790a543c9f9c4a22c4d5_light.svg)
entsteht der Glaskörper des Likörglases. Die Dicke des Glases ist dabei nicht zu berücksichtigen.
Material 1
nach rechts gekippten Glases (ohne Stiel) abgebildet ( entspricht ). Durch Rotation des Graphen von um die -Achse im Intervall entsteht der Glaskörper des Likörglases. Die Dicke des Glases ist dabei nicht zu berücksichtigen.
Material 1
5.1
Berechne das Volumen und den maximalen Umfang des Glaskörpers.
(7 BE)
5.2
Der Hersteller möchte auf dem Glas eine Markierung für die Mengenangabe „
“ (
) anbringen. Entwickle unter Angabe einer Stammfunktion einen rechnerischen Ansatz zur Ermittlung der Stelle, an der die Markierung angebracht werden muss. Das Ergebnis soll nicht ermittelt werden.
“ () anbringen. Entwickle unter Angabe einer Stammfunktion einen rechnerischen Ansatz zur Ermittlung der Stelle, an der die Markierung angebracht werden muss. Das Ergebnis soll nicht ermittelt werden.
(3 BE)
6.
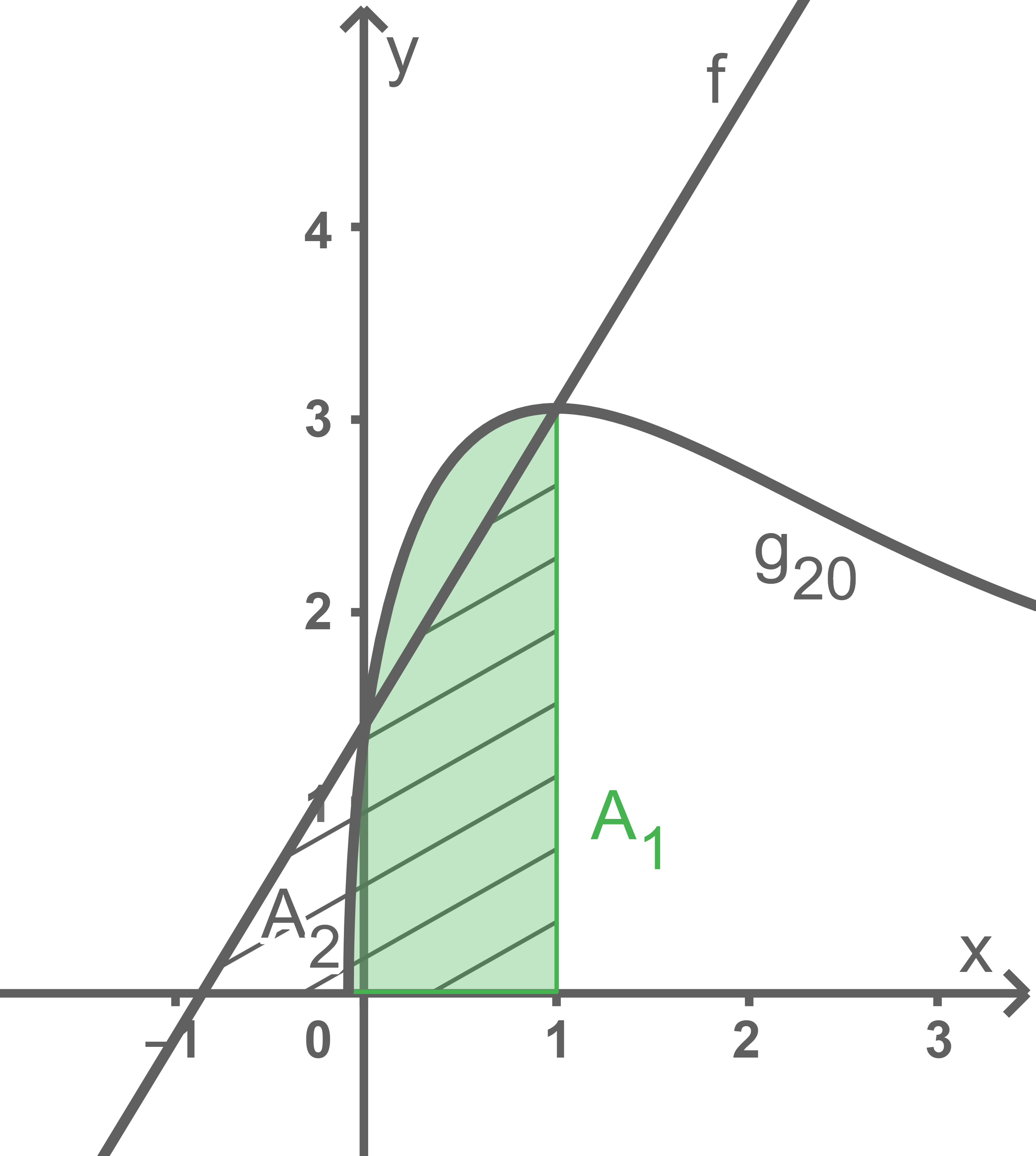
Betrachtet man die Fläche in Material 3, so ergibt sich für die grüne Fläche 
und für die schraffierte Fläche 
. Bei Rotation der Graphen der zugehörigen Randfunktionen und 
in den entsprechenden Intervallen um die -Achse erhält man für die Volumina der zugehörigen Rotationskörper
,
obwohl 
gilt.
Erkläre dieses Phänomen.
und für die schraffierte Fläche . Bei Rotation der Graphen der zugehörigen Randfunktionen und in den entsprechenden Intervallen um die -Achse erhält man für die Volumina der zugehörigen Rotationskörper
,
gilt.
Erkläre dieses Phänomen.
(5 BE)
Material 2
Material 3
1.1
Extremstelle bestätigen
Es gilt 
1. Schritt: Ableitung bilden
Mit Ketten- und Produktregel folgt für 
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
g_a](https://www.schullv.de/resources/formulas/1addef210cb7352bff859e0772b26b73310b3ce5a7ac49d4296e56431051931b_light.svg)
Da 
für alle 
, folgt mit dem Satz vom Nullprodukt:
erfüllt die notwendige Bedingung für Extremstellen und ist unabhängig von 
Da laut Aufgabenstellung auf den Nachweis der hinreichenden Bedingung verzichtet werden kann, ist für jedes 
mit 
eine Extremstelle von 
1. Schritt: Ableitung bilden
Mit Ketten- und Produktregel folgt für
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
g_a](https://www.schullv.de/resources/formulas/782e8db800b518077ff184ed4ce363be712d6e6a9854a6f227de5625e96b32f1_light.svg)
Da für alle , folgt mit dem Satz vom Nullprodukt:
![\(\begin{array}[t]{rll}
-x+1&=& 0 &\quad \scriptsize \mid\;+x \\[5pt]
1&=& x
\end{array}\)](https://www.schullv.de/resources/formulas/74a7a72d7956c3333bbe9c04bbf31d2f80d3dc902b8023a58e7c681e83f3c17b_light.svg)
erfüllt die notwendige Bedingung für Extremstellen und ist unabhängig von Da laut Aufgabenstellung auf den Nachweis der hinreichenden Bedingung verzichtet werden kann, ist für jedes mit eine Extremstelle von
1.2
Parameterwert bestimmen
Einsetzen der Koordinaten des Punktes in die Funktionsgleichung von liefert:
\begin{array}[t]{rll} a_1&=& 0 \\[5pt] a_2&\approx& 0,47 \\[5pt] \end{array}
Da 
gefordert ist, ist der gesuchte Wert 
in die Funktionsgleichung von liefert:
\begin{array}[t]{rll} a_1&=& 0 \\[5pt] a_2&\approx& 0,47 \\[5pt] \end{array}
![\(\begin{array}[t]{rll}
g_a(1)&=& a \\[5pt]
\sqrt{a\cdot 1\cdot \mathrm e^{-1} +0,1\cdot a}&=& a\\[5pt]
\sqrt{a\cdot \left(\mathrm e^{-1} + 0,1\right)}&=& a&\quad \scriptsize \mid\;^2 \\[5pt]
a\cdot\left(\mathrm e^{-1} + 0,1\right) &=& a^2 &\quad \scriptsize \mid\;- a^2 \\[5pt]
a\cdot\left(\mathrm e^{-1} + 0,1\right)-a^2&=&0 \\[5pt]
a\cdot \left(\mathrm e^{-1} + 0,1-a\right)&=& 0 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fe1f86a5994b982afcdd78c6391cf59b77377b244a9d4784db80796232e51c99_light.svg)
Anwendung des Satzes vom Nullprodukt liefert 
und:
![\(\begin{array}[t]{rll}
\mathrm e^{-1} + 0,1-a&=& 0 &\quad \scriptsize \mid\; +a \\[5pt]
\mathrm e^{-1} + 0,1&=& a_2 \\[5pt]
0,47&\approx& a_2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e595af610356e4a402171fbaf1ddaa86e361154f1ae8951229327660986b554d_light.svg)
gefordert ist, ist der gesuchte Wert
2.
Asymptote bestimmen
Die Berechnung des Grenzwertes 
liefert:
Die Graphen von nähern sich für der Asymptote 
an.
liefert:
Die Graphen von 
![\(\begin{array}[t]{rll}
\lim\limits_{x\to\infty}g_a(x)&=& \lim\limits_{x\to\infty}\sqrt{a\cdot x\cdot \mathrm e^{-x}+0,1\cdot a}&\\[5pt]
&=& \lim\limits_{x\to\infty}\sqrt{a}\cdot\sqrt{x\cdot \mathrm e^{-x}+0,1}&\\[5pt]
&=& \sqrt{a}\cdot\lim\limits_{x\to\infty}\sqrt{x\cdot \mathrm e^{-x}+0,1}&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/21014b7f98fbaf21d97c455bd90533b4f10fab05e89c94ae658eb119d2cdc87c_light.svg)
Es gilt 
da der lineare Term langsamer gegen unendlich strebt als die Exponentialfunktion gegen Null. Somit folgt:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to\infty}g_a(x)&=&\sqrt{a}\cdot \sqrt{0+0,1} \\[5pt]
&=& \sqrt{0,1a}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/94c8cb41d5c690defd810d52fe6e68bc5005e96d68115348af9b45246677b201_light.svg)
nähern sich für der Asymptote an.
3.
Stammfunktion nachweisen
Durch die Verwendung von partieller Integration wird eine Stammfunktion von 
wie folgt bestimmt:
$\displaystyle\int_{a}^{b}\left(f(x) \cdot g'(x)\right)\;\mathrm dx = \left[f(x)\cdot g(x)\right]_a^b- \displaystyle\int_{a}^{b}f'(x)\cdot g(x)\;\mathrm dx$
Mit 
folgt, dass $G_a(x) = a\cdot (-x-1)\cdot \mathrm e^{-x} + \; 0,1\cdot a\cdot x$ eine Stammfunktion von ist.
wie folgt bestimmt:
$\displaystyle\int_{a}^{b}\left(f(x) \cdot g'(x)\right)\;\mathrm dx = \left[f(x)\cdot g(x)\right]_a^b- \displaystyle\int_{a}^{b}f'(x)\cdot g(x)\;\mathrm dx$
Mit 
![\(\begin{array}[t]{rll}
\displaystyle\int\left(g_a(x)\right)^2\;\mathrm dx&=& \displaystyle\int \left(\sqrt{a\cdot x\cdot \mathrm e^{-x} +0,1\cdot a}\right)^2\;\mathrm dx \\[5pt]
&=& \displaystyle\int \left(a\cdot x\cdot \mathrm e^{-x} +0,1\cdot a\right)\;\mathrm dx \\[5pt]
&=& \displaystyle\int \left(a\cdot x\cdot \mathrm e^{-x}\right)\;\mathrm dx + \displaystyle\int \left(0,1\cdot a\right)\;\mathrm dx \\[5pt]
&=& \displaystyle\int \left(a\cdot x\cdot \mathrm e^{-x}\right)\;\mathrm dx + 0,1\cdot a\cdot x \\[5pt]
&=& a\cdot x\cdot (-1)\cdot\mathrm e^{-x}- \displaystyle\int \left(a\cdot(-1)\cdot \mathrm e^{-x}\right)\;\mathrm dx +0,1\cdot a\cdot x \\[5pt]
&=& -a\cdot x\cdot\mathrm e^{-x}+ \displaystyle\int \left(a\cdot \mathrm e^{-x}\right)\;\mathrm dx +0,1\cdot a\cdot x \\[5pt]
&=& -a\cdot x\cdot\mathrm e^{-x}+ a\cdot (-1)\cdot \mathrm e^{-x} +0,1\cdot a\cdot x +C \\[5pt]
&=&a\cdot (-x-1)\cdot \mathrm e^{-x} +0,1\cdot a\cdot x +C\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7885fdfa96abd13d1d39b33157a3542c55f8917e46cee013e6c4544c1c28fbc4_light.svg)
folgt, dass $G_a(x) = a\cdot (-x-1)\cdot \mathrm e^{-x} + \; 0,1\cdot a\cdot x$ eine Stammfunktion von ist.
4.
Nachweisen, dass alle Funktionen der Schar die gleiche Nullstelle haben
Diese Gleichung hängt nicht mehr von ab und hat laut Aufgabenstellung genau eine Lösung. Somit haben alle Funktionen die gleiche Nullstelle.
![\(\begin{array}[t]{rll}
g_a(x)&=& 0\\[5pt]
\sqrt{a\cdot x\cdot \mathrm e^{-x} +0,1\cdot a}&=& 0 &\quad \scriptsize \mid\;^2 \\[5pt]
a\cdot x\cdot \mathrm e^{-x} +0,1\cdot a&=& 0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2853fa31206b40317ba732888c25945d3051cbcb02717a986bdf2be65be4e52d_light.svg)
Da 
, darf auf beiden Seiten durch ![\(\begin{array}[t]{rll}
x\cdot \mathrm e^{-x} +0,1&=& 0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/adc8915cb3191092b712ef1c13723b66bfd09e30674038c2f4d02e54118224a6_light.svg)
ab und hat laut Aufgabenstellung genau eine Lösung. Somit haben alle Funktionen die gleiche Nullstelle.
5.1
Volumen des Glaskörpers berechnen
Das Volumen 
eines solchen Rotationskörpers im Intervall ![\([a;b]\)](https://www.schullv.de/resources/formulas/e84e12d6ffce2d83a82ceef8cfb5eb14688a4f4cce00a0d08d5357e2c6858142_light.svg)
wird mit folgender Formel berechnet:
Die Berechnung des Volumens mit den Ergebnissen aus den vorherigen Aufgabenteilen, wie z.B. einer Stammfunktion von 
liefert:
Der Glaskörper hat ein Volumen von ca. 
.
Maximalen Umfang des Glaskörpers berechnen
stellt den Radius des Glaskörpers dar. An der Stelle an der der Funktionswert von sein Maximum annimmt, ist der Umfang des Glaskörpers am größten. Die Bestimmung des Funktionswertes 
an der Extremstelle liefert:
Einsetzen in die Gleichung für den Umfang:
Der maximale Umfang des Glaskörpers beträgt ca. 
.
eines solchen Rotationskörpers im Intervall wird mit folgender Formel berechnet:
Die Berechnung des Volumens mit den Ergebnissen aus den vorherigen Aufgabenteilen, wie z.B. einer Stammfunktion von liefert:
Der Glaskörper hat ein Volumen von ca. ![\( V\approx 119,6 \,\left[\text{cm}^3\right] \)](https://www.schullv.de/resources/formulas/0436721d226eaff952c1edbcb3941b792a7d02c4345beb5e31249b9b720ca8e6_light.svg)
![\(\begin{array}[t]{rll}
V&=& \pi \cdot \displaystyle\int_{-0,09}^{9}\left(g_{20}(x)\right)^2\;\mathrm dx \\[5pt]
&=& \pi \cdot \left[ 20\cdot \left(-x-1\right)\cdot \mathrm e^{-x} + 0,1\cdot 20\cdot x\right]_{-0,09}^9 \\[5pt]
&=& \pi \cdot \left[ \left(-20x-20\right)\cdot \mathrm e^{-x} + 2\cdot x\right]_{-0,09}^9 \\[5pt]
&=& \pi \cdot\left( \left(-20\cdot 9-20\right)\cdot \mathrm e^{-9} + 2\cdot 9 -\left(\left(-20\cdot (-0,09)-20\right)\cdot \mathrm e^{-(-0,09)} + 2\cdot (-0,09)\right) \right)\\[5pt]
&=& \pi \cdot\left( -200\cdot \mathrm e^{-9} + 18 -\left(-18,2\cdot \mathrm e^{0,09} -0,18\right) \right) \\[5pt]
&=& \pi \cdot\left( -200\cdot \mathrm e^{-9} + 18 +18,2\cdot \mathrm e^{0,09} +0,18\right)\\[5pt]
&=& \pi \cdot\left( -200\cdot \mathrm e^{-9} + 18,2\cdot \mathrm e^{0,09}+ 18,18 \right) \\[5pt]
&\approx& 119,6 \,\left[\text{VE}\right] \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b7b6a51e73171b6a6ce50d7864ec35ec75f7a53163c6e0fd59306df81b626cc4_light.svg)
.
Maximalen Umfang des Glaskörpers berechnen
stellt den Radius des Glaskörpers dar. An der Stelle an der der Funktionswert von sein Maximum annimmt, ist der Umfang des Glaskörpers am größten. Die Bestimmung des Funktionswertes an der Extremstelle liefert:
Einsetzen in die Gleichung für den Umfang:
Der maximale Umfang des Glaskörpers beträgt ca. 
![\(\begin{array}[t]{rll}
r&=& g_{20}(1) \\[5pt]
&=& \sqrt{20\cdot 1\cdot \mathrm e^{-1}+0,1\cdot 20} \\[5pt]
&=& \sqrt{20\cdot \mathrm e^{-1}+2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5ad78aced4d9aeff5429a98caed2a155eea39eb6dcd5dd79194f5ae2e4982abc_light.svg)
![\( U \approx 19,22 \,[\text{cm}] \)](https://www.schullv.de/resources/formulas/0963e3d22a0bf23eef9ebfb18ad250449a2b0660af06bd27ffee666836abb86b_light.svg)
![\(\begin{array}[t]{rll}
U&=& 2\cdot \pi \cdot r \\[5pt]
&=& 2\cdot \pi \cdot \sqrt{20\cdot \mathrm e^{-1}+2} \\[5pt]
&\approx& 19,22 \,[\text{cm}]\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c8c2228e880f951f1099dfb7552017ae98dfa9dc90e624b341cc3d40cc8b3614_light.svg)
.
5.2
Rechnerischen Ansatz entwickeln
Ist das Glas bis zur Stelle 
gefüllt, wird das entsprechende Volumen mit Hilfe eines Rotationsvolumens wie in Aufgabe 5.1 berechnet.
Es gilt also 
sodass folgt:
gefüllt, wird das entsprechende Volumen mit Hilfe eines Rotationsvolumens wie in Aufgabe 5.1 berechnet.
Es gilt also sodass folgt:
![\(\begin{array}[t]{rll}
V&=& 20\\[5pt]
\pi \cdot \displaystyle\int_{-0,09}^{t}\left(g_{20}(x)\right)^2\;\mathrm dx&=& 20 \\[5pt]
\pi \cdot \left[20\cdot (-x-1)\cdot \mathrm e^{-x} + 0,1\cdot 20 \cdot x\right]_{-0,09}^t&=& 20\\[5pt]
\pi \cdot \left[20\cdot (-x-1)\cdot \mathrm e^{-x} + 2\cdot x\right]_{-0,09}^t&=& 20 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6920dc4c0dfacad156259170cf1bd0542852431f456c99ed302aa2164ef3a589_light.svg)
6.
Phänomen erklären
Bei der Berechnung des Rotationsvolumens wird, anders als bei der Berechnung des Flächeninhalts, über den quadrierten Funktionsterm integriert.
Die Erklärung lautet demnach:
Große Abweichungen der Funktionswerte nach oben haben einen größeren Einfluss auf das Volumen als auf den Flächeninhalt.
Die Fläche, die nur in
und nicht in 
liegt, ist im Bereich 
deutlich über dem Graphen von . Im Ausgleich dafür schließt der Graph von im Bereich von ungefähr 
mit der -Achse eine Fläche im positiven 
-Bereich ein, welche größer als die vorherige ist. Da diese Fläche im Vergleich zur ersten Fläche deutlich näher an der -Achse liegt, hat sie einen kleineren Einfluss auf das Rotationsvolumen und es folgt 
Die Fläche, die nur in
und nicht in liegt, ist im Bereich deutlich über dem Graphen von . Im Ausgleich dafür schließt der Graph von im Bereich von ungefähr mit der -Achse eine Fläche im positiven -Bereich ein, welche größer als die vorherige ist. Da diese Fläche im Vergleich zur ersten Fläche deutlich näher an der -Achse liegt, hat sie einen kleineren Einfluss auf das Rotationsvolumen und es folgt