A2 - Analysis

Die folgende Abbildung zeigt die Graphen einer Funktion der Funktionenschar $f_k$ mit $f_k(x) = \sin(x) + k\cdot x, \; k \in \mathbb{R}$ , und ihrer Ableitungsfunktion zu sehen.

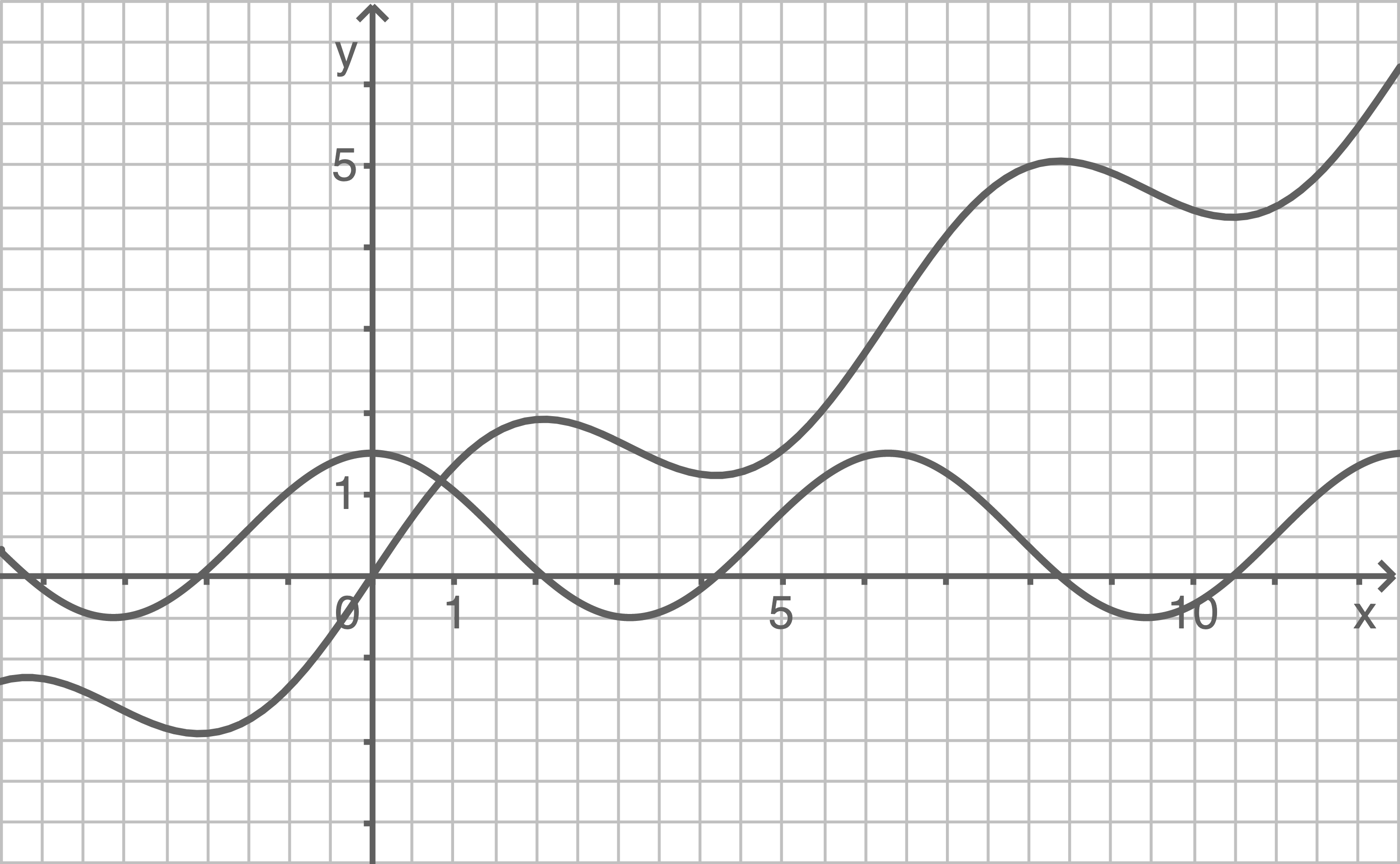
1.1

Gib die erste Ableitung von $f_k$ an. Beschrifte die Graphen im Material jeweils mit der zugehörigen Funktion.
Bestimme $k$ für die im Material abgebildeten Funktionsgraphen.

(4 BE)

1.2

Untersuche unter Einbeziehung der Eigenschaften des Graphen der Ableitungsfunktion, für welche Werte von $k$ die Scharfunktionen $f_k$ Extremstellen haben.

(5 BE)

1.3

Skizziere im Material die Fläche zwischen dem Graphen von $f_k$ und der Geraden mit der Gleichung $y = k\cdot x$ über dem Intervall $[0;2\pi]$ für den in Aufgabe 1.1 bestimmten Wert von $k$ .

(2 BE)

1.4

Betrachtet werden für jede Scharfunktion $f_k$ die Flächenstücke zwischen dem Graphen von $f_k$ und der Geraden mit der Gleichung $y = k\cdot x$ , die jeweils von zwei aufeinanderfolgenden Schnittpunkten begrenzt werden.

Zeige mithilfe geeigneter Rechnungen, dass alle diese Flächenstücke unabhängig von $k$ gleich groß sind.

(5 BE)

Der Temperaturverlauf eines Tages (gemessen in °C) in Abhängigkeit von der Zeit t (gemessen in Stunden) kann modellhaft durch eine Funktion $g$ dargestellt werden, die folgende Form hat:

$g(t)= a\cdot \sin\left(\dfrac{1}{12}\pi \cdot (t-b)\right)+c,$ $\; t\in \mathbb{R}, \; 0\leq t\leq 24\;\;$ $\;\;a, b,c \in \mathbb{R}$

An einem bestimmten Tag wird um 4 Uhr morgens die tiefste Tagestemperatur von 16 °C gemessen. Im Laufe des Tages steigt die Temperatur auf einen Maximalwert von 26 °C an.

Bestimme unter Nutzung deiner Kenntnisse über die Eigenschaften der Sinusfunktion zu den gegebenen Daten passende Werte für die Parameter $a$ , $b$ und $c$ .
Beschreibe die Bedeutung der Parameter im Sachzusammenhang.

(8 BE)

An einem bestimmten Tag wird in der Stadt Frankfurt am Main der Temperaturverlauf annähernd durch die Funktion $h$ beschrieben mit
$h(t)=-6 \cdot \sin\left(\dfrac{\pi}{12}t + \dfrac{\pi}{12}\right)+ 0,4t +10,5,$ $\; t\in \mathbb{R}, \; 0\leq t\leq24$
(t in Stunden, h(t) in °C auf eine Nachkommastelle genau angegeben).

3.1

Untersuche, zu welcher Uhrzeit die minimale und zu welcher Uhrzeit die maximale Temperatur erreicht wird.
Hinweis: Eine Betrachtung der Randwerte ist nicht erforderlich.

(9 BE)

3.2

Liegen nur wenige Temperaturmessungen vor, wird die mittlere Tagestemperatur näherungsweise nach der Formel
$T_L =\dfrac{1}{4}\left(T_0 + T_6 + T_{12} + T_{18} \right)$
berechnet, wobei $T_0$ , $T_6$ , $T_{12}$ und $T_{18}$ die gemessenen Temperaturen zu den sogenannten „synoptischen Stunden“ um 0, 6, 12 und 18 Uhr des Tages bezeichnen.
Berechne mit Hilfe von $h$ und dieser Formel die mittlere Tagestemperatur an diesem Tag.

(3 BE)

3.3

Mit $\overline{T}=\dfrac{1}{24}\displaystyle\int_{0}^{24} h(t) \;\mathrm dt$ kann ebenfalls eine sinnvolle mittlere Tagestemperatur berechnet werden. Berechne damit die mittlere Tagestemperatur in Frankfurt an diesem Tag.
Berechne zudem die prozentuale Abweichung der Näherung durch die „synoptische Stunden“-Formel aus Aufgabe 3.2 vom hier berechneten Wert von $\overline{T}$ .

(4 BE)

1.1

Erste Ableitung angeben

$f_k(x)=\sin(x) + k \cdot x$ ; $k\in \mathbb{R}$

$\(f$ ; $k\in \mathbb{R}$

Graphen beschriften

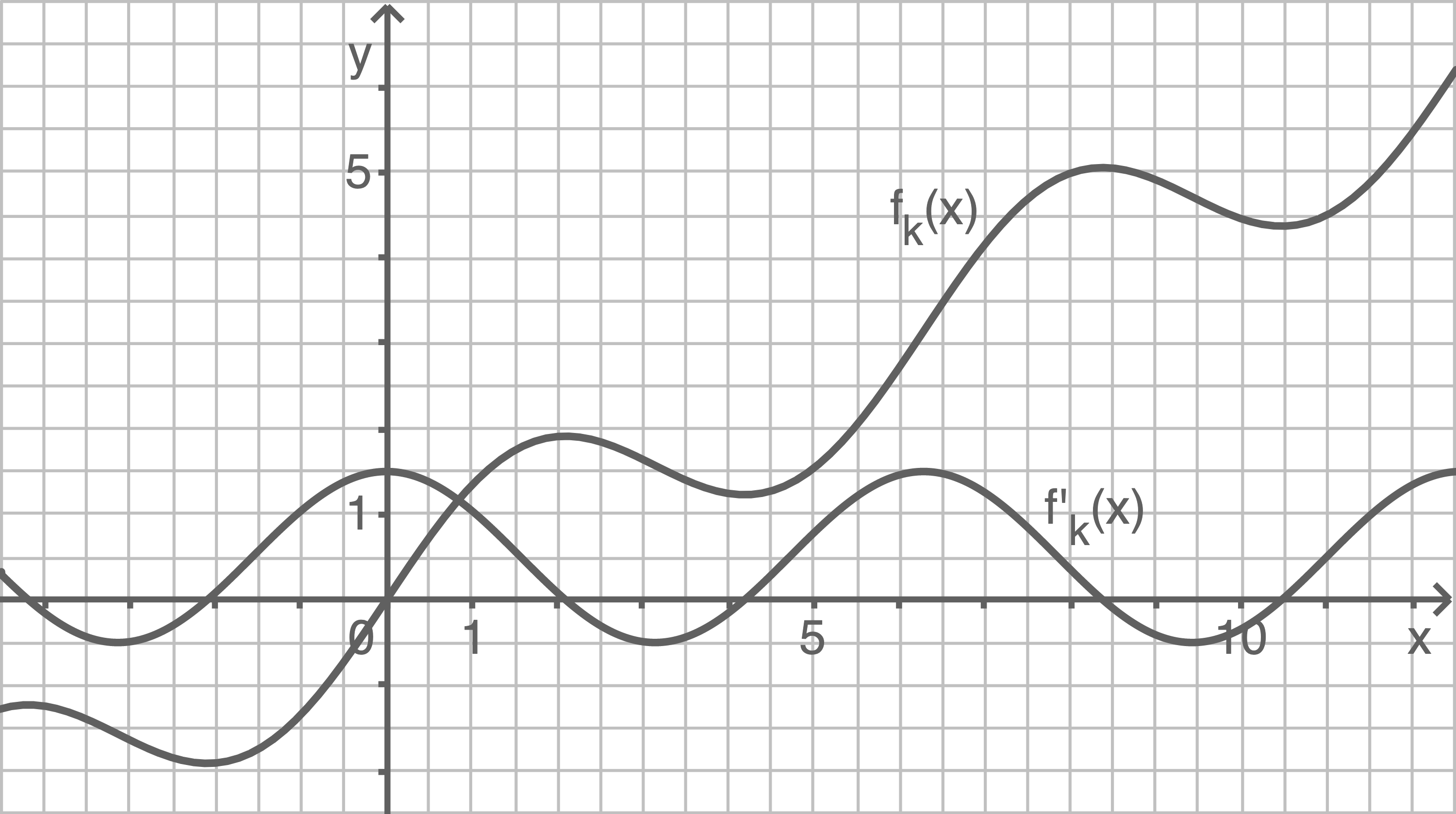Beschriftung Funktionenschar Hessen Abi 2015

Parameter $k$ bestimmen

Der Parameter $k$ kann durch eine Punktprobe mit einem Punkt auf dem Graphen von $f_k$ oder $\(f$ bestimmt werden.

Aus der Abbildung kann beispielsweise der Punkt $P(0\mid 1,5)$ entnommen werden.

$\(\begin{array}[t]{rll} f$

1.2

1. Schritt: Notwendige Bedingung untersuchen

Die notwendige Bedingung besagt, dass für eine Extremstelle der Funktionsterm der Ableitung gleich Null ist. Hierbei handelt es sich grafisch um eine Nullstelle der ersten Ableitung.

Es muss also gelten:

$\(\begin{array}[t]{rll} f$

Da der Cosinus nur Werte von -1 bis 1 annimmmt, besitzt die Ableitung somit für $k \gt 1$ und $k \lt -1$ keine Nullstellen. $k$ muss also im Intervall $\left[-1,1\right]$ liegen.

2. Schritt: Hinreichende Bedingung prüfen

Die hinreichende Bedingung besagt, dass die zweite Ableitung an der potentiellen Extremstelle ungleich Null ist. Damit ist die Steigung der Ableitung an den Nullstellen ungleich Null und es findet ein Vorzeichenwechsel statt.

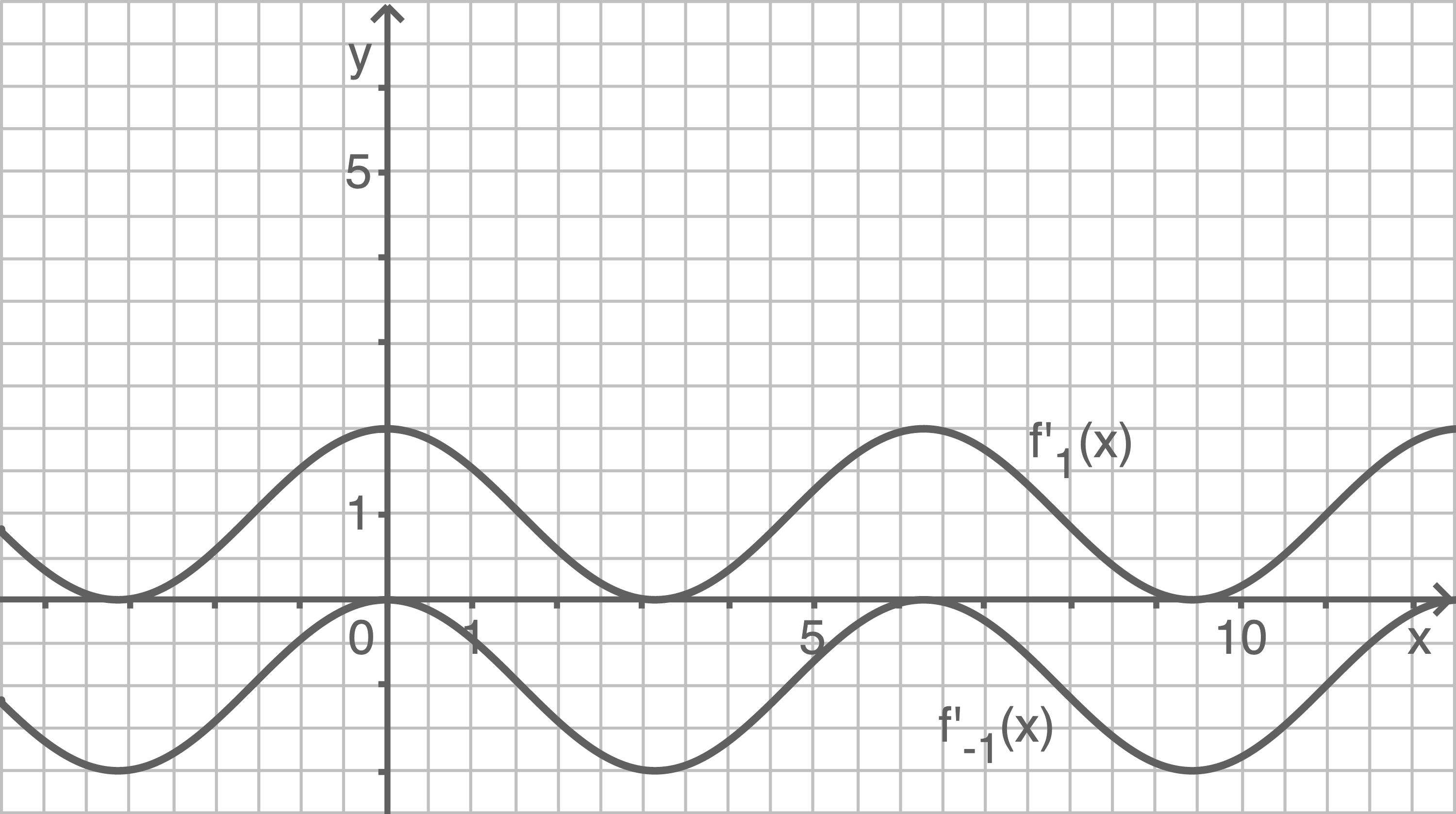Hilfsskizze Hinreichende Bedingung Hessen Abi 2015

Wie in der Skizze erkennbar, findet im Fall $k=1$ und $k=-1$ kein Vorzeichenwechsel statt, da dort der Cosinus die $x$ -Achse nur berührt und nicht schneidet.

Die Funktionenschar $f_k$ besitzt folglich nur für $k \in \left(-1,1\right)$ Extremstellen.

1.3

Aus Aufgabe 1.1 folgt $k=0,5$ und somit $y=0,5x.$
Die Intervallgrenze $2\pi$ entspricht etwa $6,3.$

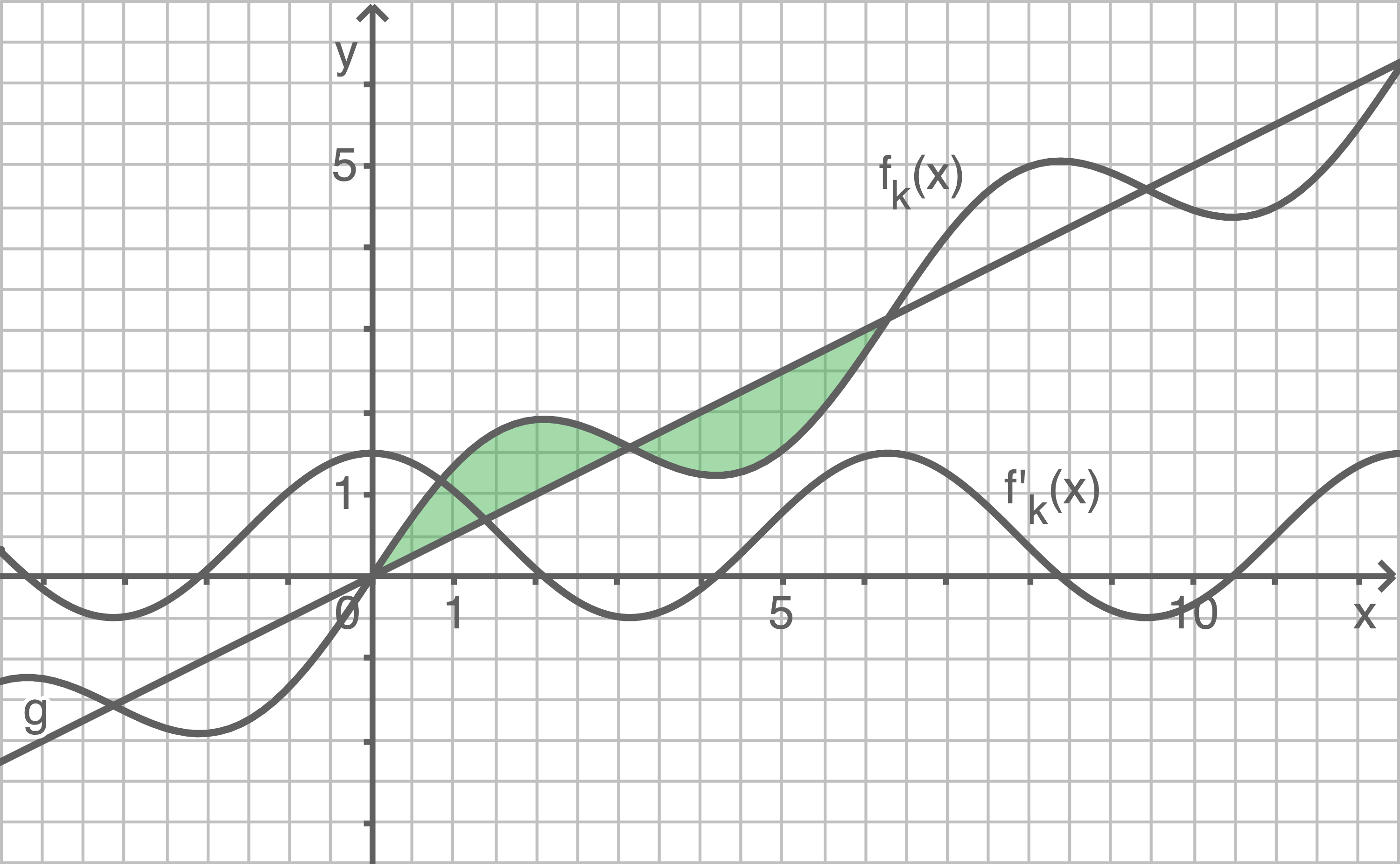
Flaecheninhalt Funktionenschar Hessen Abi 2015

1.4

Die Größe eines Flächenstücks entspricht dem Flächeninhalt zwischen dem Graphen der Funktionenschar $f_k$ und der Geraden $y=k \cdot x$ .

1. Schritt: Schnittpunkte berechnen

$\begin{array}[t]{rll} f_k(x) &=&k\cdot x & \\[5pt] \sin(x) + k \cdot x&=&k\cdot x& \quad \scriptsize \mid\; - k \cdot x\\[5pt] \sin(x)&=&0& \\[5pt] \end{array}$

Aufgrund der Eigenschaften der Sinus-Funktion gilt $\sin(x)=0$ für alle $x=z\cdot \pi$ mit $z \in \mathbb{Z}.$ Die Schnittpunkte sind dementsprechend alle ganzzahlige Vielfache von $\pi$ .

2. Schritt: Flächeninhalte berechnen

Die Flächenstücke sind durch zwei aufeinander folgende Schnittpunkte begrenzt. Ist $z \cdot \pi$ ein Schnittpunkt, so ist der nächste Schnittpunkt $\left(z+1\right) \cdot \pi$ .

Der Flächeninhalt eines Flächenstücks lässt sich also wie folgt berechnen:

Rechenweg anzeigen

$A=2$

Der Betrag der Fläche des Cosinus ist auf jedem Intervall $\left[z \cdot \pi; \left( z+1 \right ) \cdot \pi\right]$ gleich 2.

Der Flächeninhalt $A$ eines Flächenstücks ist somit immer gleich groß und unabhängig vom Parameter $k$ .

Parameter bestimmen

Da um 4 Uhr morgens die tiefste Temperatur von $16 ^{\circ}C$ gemessen wird, ist der Punkt $T (4 \mid 16)$ Tiefpunkt von $g.$

Da $a$ und $c$ konstant sind, nimmt die Funktion $g$ genau dann ihr Minimum/Maximum an, wenn der Sinus minimal/maximal ist.

Das Minimum des Sinus ist $-1$ , somit ergibt sich:

$\sin\left(\dfrac{1}{12}\pi \cdot \left( 4-b\right)\right)=-1$

(Alternativ kann hier auch das Maximum 1 angenommen werden, der alternative Lösungsweg ist am Ende der Lösung zu finden.)

Außerdem erhalten wir für $g(4)$ eine zweite Bedingung:

$\begin{array}[t]{rll} g(4)&=& 16& \\[5pt] a \cdot \left(\sin\left(\dfrac{1}{12}\pi \cdot \left( 4-b\right)\right) \right)+c&=& 16 & \\[5pt] a \cdot \left( -1 \right) +c&=& 16& \\[5pt] (-a) + c &=& 16 \end{array}$

Die dritte Bedingung lautet, dass zu einem unbekannten Zeitpunkt $t_u$ die Temperatur ihren Maximalwert annimmt, der Sinus also sein Maximum/Minimum annimmt.

Das Maximum der Sinusfunktion ist $1.$ Somit folgt:

$\begin{array}[t]{rll} g(t_u)&=& 26 & \\[5pt] a \cdot \left(\sin\left(\dfrac{1}{12}\pi \cdot \left( t_u-b\right)\right) \right)+c &=& 26 & \\[5pt] a \cdot 1 +c&=& 26 & \\[5pt] a+c&=& 26 & \\[5pt] \end{array}$

Aus den drei Bedingungen ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrcl} \text{I}\quad&\sin\left(\dfrac{1}{12}\cdot \pi \cdot \left( 4-b\right)\right)&=&-1&\\[5pt] \text{II}\quad&(-a) + c &=& 16\\[5pt] \text{III}\quad&a+c&=&26 \end{array}$

1. Schritt: Bedingung $\text{I}$ auflösen

Die Gleichung $\sin(z)=-1$ ist beispielsweise für $z=-\dfrac{1}{2}\pi$ erfüllt.

Durch Substitution ergibt sich:

Rechenweg anzeigen

$b=10$

(Da die Sinusfunktion periodisch verläuft, können auch andere Werte für $z$ gewählt werden. Für beispielsweise $z=\dfrac{3}{2}\pi$ folgt $b=-14$ . Dies verändert nichts an den folgenden Rechnungen.)

2. Schritt: Bedingung $\text{II}$ und $\text{III}$ auflösen

Das lineare Gleichungssystem kann mit dem Einsetzungsverfahren gelöst werden:

Rechnung anzeigen

Damit sind die Parameter beispielsweise durch $a=5$ , $b=10$ beziehungsweise $b=-14$ und $c=21$ gegeben.

Eine mögliche Funktionsgleichung lautet folglich:

$g(t)= 5 \cdot \sin\left(\dfrac{1}{12}\pi \cdot \left( t -10 \right)\right) + 21$

Alternativer Lösungsweg

Wird anfangs der Sinus gleich 1 gewählt, so folgt beispielsweise $b=-2$ . Des Weiteren ändert sich das Vorzeichen von $a$ in den Gleichungen $\text{II}$ und $\text{III}$ . Es ergibt sich also $a=-5$ . Der Parameter $c$ ändert sich nicht.

Parameter deuten

Der Verlauf der Temperatur ist periodisch und schwankt um den Mittelwert $21^{\circ}C$ . Dieser Mittelwert wird durch den Parameter $c=21$ bestimmt.

Die Schwankung zwischen dem Temperaturtiefpunkt von $16^{\circ}C$ und der höchsten Temperatur von $26^{\circ}C$ beträgt $10^{\circ}C$ . Die Amplitude beträgt also $5^{\circ}C$ und wird folglich durch den Parameter $a=5$ bestimmt.

Die Funktion $g$ hat eine Periodenlänge von 24 Stunden und würde ohne zeitliche Verschiebung das Maximum nach 6 Stunden und das Minimum nach 18 Stunden annehmen. Der Parameter $b=10$ beziehungsweise $b=-14$ gibt hier die zeitliche Verschiebung an, so dass $g$ das Minimum zum Zeitpunkt $t=4$ annimmt.

Die Funktion $g$ beschreibt also den periodischen Verlauf der Tagestemperatur um den Mittelwert $c$ mit einer maximalen Abweichung nach unten beziehungsweise oben von $a$ und einer zeitlichen Verschiebung um $b$ .

3.1

1. Schritt: Ableitungen berechnen

Mit der Kettenregel folgt:

$h(t)=...$

Funktion anzeigen

$\( h$

Erste Ableitung anzeigen

$\( h$

Zweite Ableitung anzeigen

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\( h$

Rechnung anzeigen

Durch Substitution mit $z=\dfrac{\pi}{12} \cdot t + \dfrac{\pi}{12}$ ergibt sich folgende Gleichung: $\cos\left(z\right)= \dfrac{4}{5\pi}$ .

Diese besitzt auf dem Intervall $\left[0,2\pi\right]$ zwei Lösungen $z_1$ und $z_2$ :

$z_1$ kann durch $\cos^{-1}\left(\dfrac{4}{5\pi}\right)$ mit deinem Taschenrechner berechnet werden. Es ergibt sich $z_1=1,3133.$

Wegen den Eigenschaften der Cosinusfunktion gilt außerdem: $\cos(z)=\cos(2\pi - z)$ .

Es ergibt sich also $z_2$ mit:

$z_2=2\pi - z_1=4,9699$

Durch Resubstitution mit $t=\dfrac{12}{\pi} \cdot \left( z - \dfrac{\pi}{12}\right)$ folgen die möglichen Extremstellen:

$\begin{array}[t]{rll} t_1&=&\dfrac{12}{\pi} \cdot \left( z_1 - \dfrac{\pi}{12}\right) & \\[5pt] &=&\dfrac{12}{\pi} \cdot \left( 1,3133 - \dfrac{\pi}{12}\right) &\\[5pt] &=& 4,02 \end{array}$

$\begin{array}[t]{rll} t_2&=&\dfrac{12}{\pi} \cdot \left( z_2 - \dfrac{\pi}{12}\right) & \\[5pt] &=&\dfrac{12}{\pi} \cdot \left( 4,9699 - \dfrac{\pi}{12}\right) & \\[5pt] &=& 17,98 \end{array}$

3. Schritt: Hinreichende Bedingung für Extremstellen prüfen

$\(\begin{array}[t]{rll} h$

Etwa um 4 Uhr morgens ist somit die Temperatur minimal und um circa 18 Uhr ist die Temperatur maximal.

3.2

1. Schritt: Temperaturen $T_0$ , $T_6$ , $T_{12}$ , $T_{18}$ berechnen

Mithilfe der Funktion $h$ und dem Zusammenhang $\; T_t=h(t)$ lassen sich die Temperaturen $T_t$ zu den „synoptischen Stunden“ bestimmen:

$T_0=8,95$

Rechenweg anzeigen

$T_6=7,1$

Rechenweg anzeigen

$T_{12}=16,85$

Rechenweg anzeigen

$T_{18}=23,5$

Rechenweg anzeigen

2. Schritt: Mittlere Tagestemperatur berechnen

Rechenweg anzeigen

$T_L=14,1$

Die mittlere Tagestemperatur $T_L$ beträgt somit etwa $14,1^{\circ}C.$

3.3

Mittlere Tagestemperatur berechnen

Stammfunktion $H$ bestimmen:

$H(t)=...$

Stammfunktion anzeigen

Mithilfe der Formel aus der Aufgabenstellung folgt nun:

Rechenweg anzeigen

$\overline{T}=15,3$

Die mittlere Tagestemperatur $\overline{T}$ beträgt somit $15,3^{\circ}C.$

Prozentuale Abweichung $\Delta T$ berechnen

$\begin{array}[t]{rll} \Delta T&=& \dfrac{\overline{T}-T_L}{\overline{T}}& \\[5pt] &=& \dfrac{15,3-14,1}{15,3}& \\[5pt] &=&\dfrac{1,2}{15,3} & \\[5pt] &=& 7,84 \% \end{array}$