B1 - Analytische Geometrie

Drei Punkte $A_t$ , $B_t$ und $C_t$ bewegen sich jeweils entlang einer Geraden:

$A_t$ auf der Geraden $g_a: \vec{a}_t = \pmatrix{1\\0\\0}+t\cdot\pmatrix{0\\0\\1},$

$B_t$ auf der Geraden $g_b: \vec{b}_t = \pmatrix{0\\1\\0}+t\cdot\pmatrix{1\\0\\0},$

$C_t$ auf der Geraden $g_c: \vec{c}_t = \pmatrix{0\\0\\1}+t\cdot\pmatrix{0\\1\\0}$

Die Punkte $A_t$ , $B_t$ und $C_t$ bilden für alle $t\in\mathbb{R}$ ein Dreieck $\Delta_t.$

1.1

Zeichne in das Koordinatensystem (Abbildung 1) die drei Geraden sowie die Dreiecke $\Delta_0,$ $\Delta_1$ und $\Delta_2$ ein.

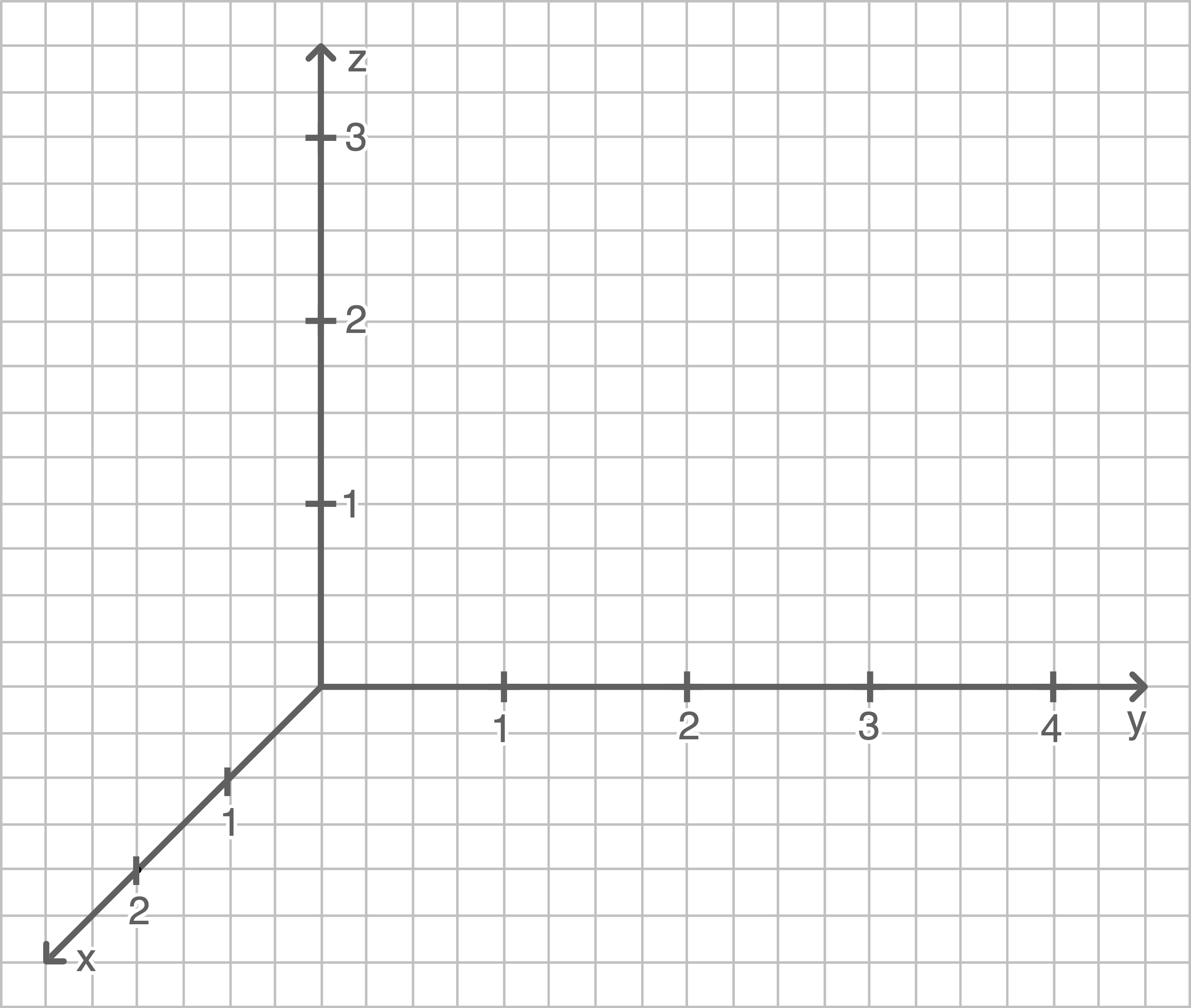
Abbildung 1

(4 BE)

1.2

Untersuche, ob die Dreiecke $\Delta_t$ gleichseitig sind.

(3 BE)

1.3

Die Punkte $A_t$ , $B_t$ und $C_t$ legen für jedes $t$ eine Ebene $E_t$ fest.

Bestimme eine Ebenengleichung der Ebene $E_t$ in Parameterform.

Zeige, dass $\vec{n}=\pmatrix{t^{2}-t+1\\t^{2}-t+1\\t^{2}-t+1}$ ein Normalenvektor von $E_t$ ist, und begründe damit die Parallelität der Ebenen.

Bestimme den Abstand zweier beliebiger dieser Ebenen $E_t$ und $E_{t+k}$ mit $k\in\mathbb{R}$ .

(11 BE)

1.4

Erläutere die in im Folgenden durchgeführten Rechenschritte und das Ergebnis im Sachzusammenhang.

$(1) \quad \overline{AB}=\pmatrix{t-1\\1\\-t}; \quad \overline{AC}=\pmatrix{-1\\t\\1-t}$

$(2) \quad A(t)= \dfrac{1}{2} \cdot \left|\pmatrix{t-1\\1\\-t}\times \pmatrix{-1\\t\\1-t} \right|$

$(3) \quad A(t)=\dfrac{\sqrt{3}\cdot (t^2-t+1)}{2}$

$\((4) \quad A$

$(5) \quad \dfrac{\sqrt{3}\cdot(2\cdot t-1)}{2}=0 \; \Rightarrow \; t=\dfrac{1}{2}$

$\((6) \quad A$

(4 BE)

Die Punkte $A_t,$ $B_t$ und $C_t$ bilden zusammen mit dem Ursprung eine Schar von Pyramiden in Abhängigkeit von $t.$ Das Volumen einer solchen Pyramide kann mit der Formel $V(t)=\dfrac{1}{6}\cdot\left|\left(\vec{a}_{t} \times\vec{b}_{t}\right)\cdot\vec{c}_{t}\right|$ berechnet werden.

2.1

Zeige, dass $V(t)=\dfrac{1}{6}\cdot\left|\left(t^{3}+1\right)\right|$ gilt, und bestimme $t$ so, dass das Volumen $V(t)$ den Wert $\dfrac{3}{2}$ annimmt.

(4 BE)

2.2

Untersuche, ob die Pyramide mit der minimalen Grundfläche auch die Pyramide mit dem minimalen Volumen ist.

(4 BE)

1.1

1. Schritt: Geraden einzeichnen

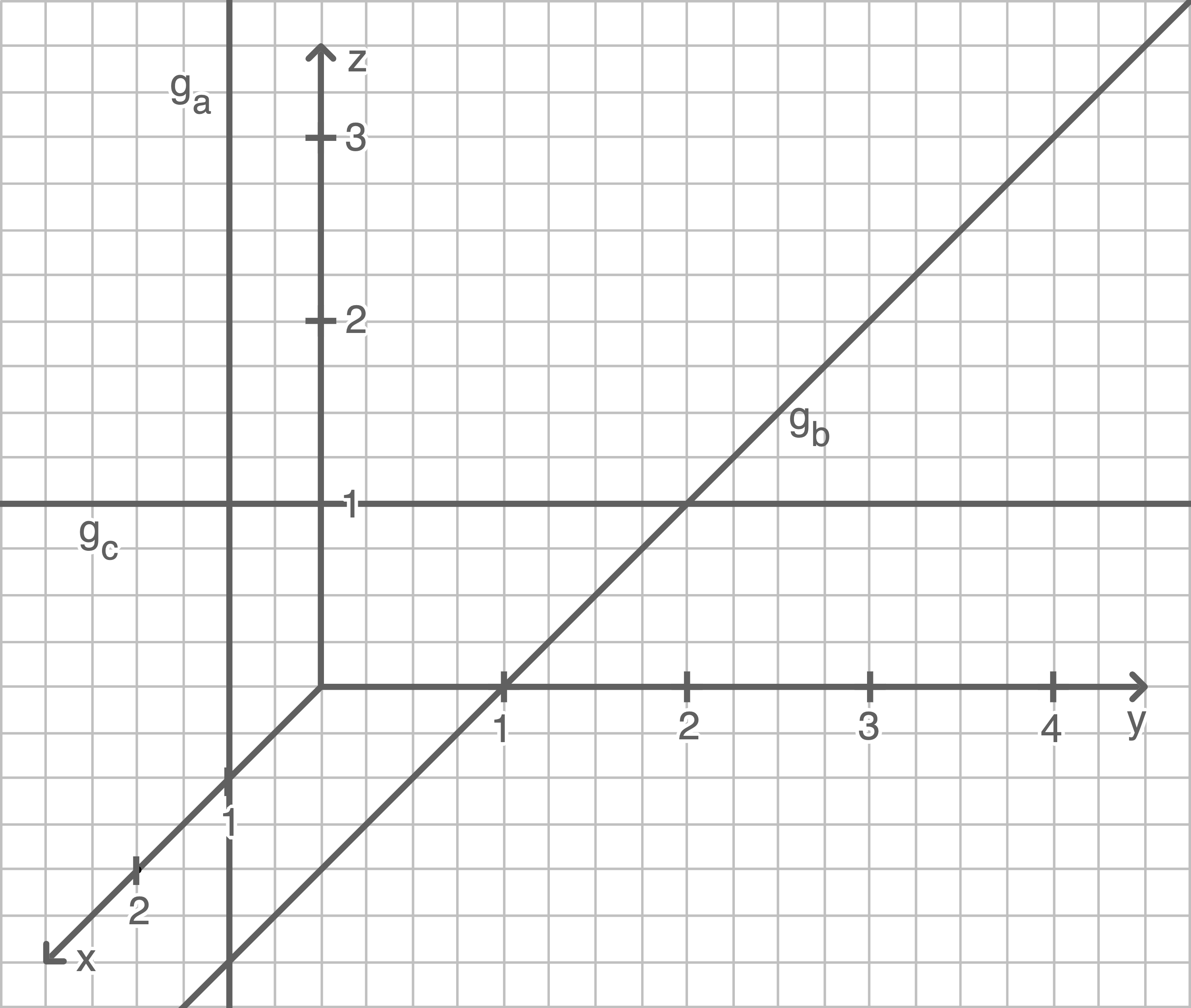2. Schritt: Dreiecke einzeichnen

Jede Gerade lässt sich als allgemeiner Punkt darstellen:

$A_t=(1\mid0\mid t)$ , $B_t=(t\mid1 \mid0)$ , $C_t=(0\mid t\mid 1)$

Für $\Delta_0$ , $\Delta_1$ , $\Delta_2$ folgen somit die Punkte:

$A_0=(1\mid0\mid 0)$ , $B_0=(0\mid1 \mid0)$ , $C_0=(0\mid 0\mid 1)$

$A_1=(1\mid0\mid 1)$ , $B_1=(1\mid1 \mid0)$ , $C_1=(0\mid 1\mid 1)$

$A_2=(1\mid0\mid 2)$ , $B_2=(2\mid1 \mid0)$ , $C_2=(0\mid 2\mid 1)$

Eintragen in das Koordinatensystem liefert nun:

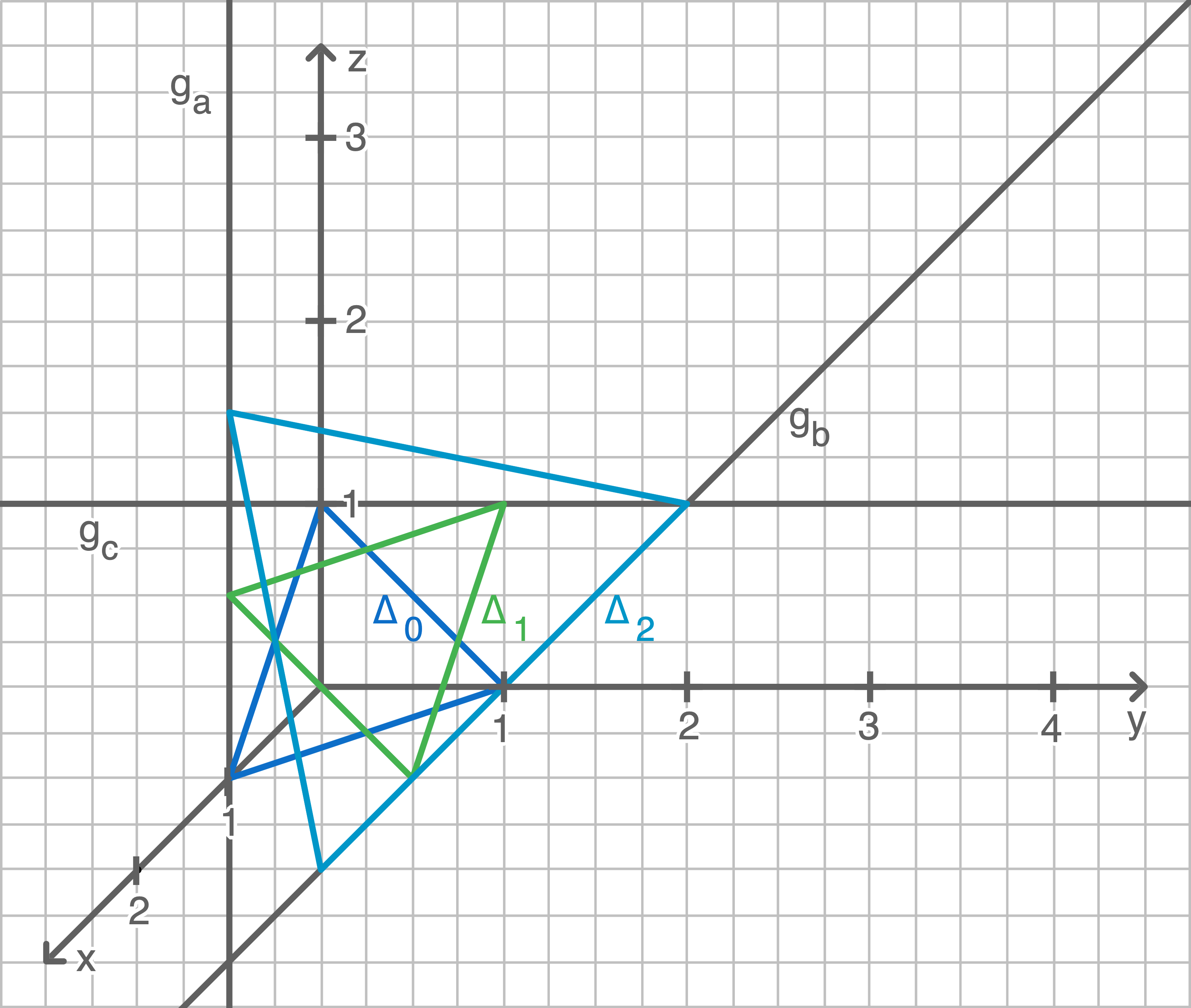
1.2

Ein Dreieck ist genau dann gleichseitig, wenn alle drei Seiten genau gleich lang sind.

$\begin{array}[t]{rll} \,\bigg \vert \,\overrightarrow{A_tB_t}\,\bigg \vert \, &=& \left| \pmatrix{t-1\\1-0\\0-t} \right|& \\[5pt] &=& \sqrt{(t-1)^2+1^2+(-t)^2}& \\[5pt] &=&\sqrt{t^2-2t+1+1+t^2} \end{array}$

$\begin{array}[t]{rll} \,\bigg \vert \,\overrightarrow{A_tC_t}\,\bigg \vert \, &=& \left| \pmatrix{0-1\\t-0\\1-t} \right|& \\[5pt] &=& \sqrt{(-1)^2+t^2+(1-t)^2}& \\[5pt] &=&\sqrt{1+t^2+t^2-2t+1} \end{array}$

$\begin{array}[t]{rll} \,\bigg \vert \,\overrightarrow{B_tC_t}\,\bigg \vert \, &=& \left|\pmatrix{0-t\\t-1\\1-0} \right|& \\[5pt] &=& \sqrt{(-t)^2+(t-1)^2+1^2}& \\[5pt] &=& \sqrt{t^2+t^2-2t+1+1} \end{array}$

Wegen $\,\bigg \vert \,\overrightarrow{A_tB_t}\,\bigg \vert \, = \,\bigg \vert \,\overrightarrow{A_tC_t}\,\bigg \vert \, = \,\bigg \vert \,\overrightarrow{B_tC_t}\,\bigg \vert \,$ gilt, dass die Dreiecke $\Delta_t$ folglich gleichseitig sind.

1.3

Ebenengleichung aufstellen

Ein Stützvektor der Ebene ist beispielsweise gegeben durch $\overrightarrow{OA_t}=\pmatrix{1\\0\\t}.$ Zwei Richtungsvektoren der Ebene $E_t$ sind $\overrightarrow{A_tB_t}=\pmatrix{t-1\\1\\-t}$ und $\overrightarrow{A_tC_t}=\pmatrix{-1\\t\\1-t}.$

Eine Ebenengleichung von $E_t$ in Parameterform folgt somit beispielsweise mit:

Ebenengleichung anzeigen

Normalenvektor nachweisen

Das Kreuzprodukt der beiden Richtungsvektoren liefert:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \pmatrix{t-1\\1\\-t}\times \pmatrix{-1\\t\\1-t}&\\[5pt] &=& \pmatrix{(t-1)\cdot t-1\cdot (-1)\\1\cdot (1-t)-(-t)\cdot t\\ (-t)\cdot 1-(t-1)\cdot (1-t)} &\\[5pt] &=& \pmatrix{t^2-t+1\\t^2-t+1\\t^2-t+1}&\\[5pt] \end{array}$

Somit ist $\overrightarrow{n}=\pmatrix{t^2-t+1\\t^2-t+1\\t^2-t+1}$ ein Normalenvektor von $E_t.$

Parallelität begründen

Die Normalenvektoren $\vec{n}_t$ sind für alle eingesetzten Parameter Vielfache voneinander und damit identisch. Folglich sind alle Ebenen $E_t$ parallel zueinander.

Abstand berechnen

Koordinatenform von $E_t$ aufstellen:

Rechenweg anzeigen

$(t^2-t+1)\cdot (x_1+x_2+x_3)=d$

Einsetzen der Koordinaten von $A_t$ liefert:

$\begin{array}[t]{rll} E_t: (t^2-t+1)\cdot (1+0+t)&=& d & \\[5pt] t^2-t+1+ (t^2-t+1)\cdot t&=& d & \\[5pt] t^3+1&=& d \end{array}$

Die Hesse'sche Normalform ergibt sich zu:

Gleichung anzeigen

Ein Stützvektors von $E_{t+k}$ ist beispielsweise $S(1\mid 0\mid t+k).$ Es folgt also:

Rechenweg anzeigen

$d(E_t,S)= \left|\dfrac{k}{\sqrt{3}}\right| \; [\text{LE}]$

Der Abstand zwischen zwei Ebenen $E_t$ und $E_{t+k}$ beträgt somit $\left| \dfrac{k}{\sqrt{3}}\right|$ Längeneinheiten.

1.4

Schritt $\boldsymbol{(1)}$

Es werden die Verbindungsvektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ berechnet (siehe auch Aufgabe 1.3).

Schritt $\boldsymbol{(2)}$

Im zweiten Schritt wird eine Formel aufgestellt, um den Flächeninhalt eines Dreiecks $\Delta_t$ abhängig von $t$ zu bestimmen.

Der Betrag des Kreuzprodukts zweier Vektoren bildet den Flächeninhalt des von den Vektoren aufgespannten Parallelogramms. Da es sich um ein Dreieck handelt, wird dieser halbiert.

Schritt $\boldsymbol{(3)}$

Das Kreuzprodukt aus dem zweiten Schritt wird ausgerechnet und ergibt sich zu $\sqrt{3}\cdot (t^2-t+1).$

Schritt $\boldsymbol{(4)}$

In diesem Rechenschritt werden die erste und die zweite Ableitung dieser Funktion $A(t)$ gebildet.

Schritt $\boldsymbol{(5)}$

Die Funktion zur Berechnung des Flächeninhalts wird auf Extrenmstellen untersucht. Es wird die notwendige Bedingung für Extremstellen angewendet und die Nullstelle der ersten Ableitungsfunktion berechnet, indem die Ableitung gleich Null gesetzt wird und nach $t$ aufgelöst wird.

Die Stelle $t=\dfrac{1}{2}$ stellt somit eine mögliche Extremstelle dar.

Schritt $\boldsymbol{(6)}$

Da es sich auch um einen Sattelpunkt handeln könnte, wird nun die hinreichende Bedingung für Extremstellen überprüft.

Die zweite Ableitung ist mit $t=\dfrac{1}{2}$ größer als Null, somit handelt es sich bei dem Extremum um ein Minimum. Für den Parameterwert $t=\dfrac{1}{2}$ nimmt das Dreieck $\Delta_t$ also seinen minimalen Flächeninhalt an.

2.1

Volumen nachweisen

Es gilt:

Rechenweg anzeigen

$V(t)=\dfrac{1}{6}\cdot\left|(t^3+1)\right|$

Damit gilt $V(t)=\left|(t^3+1)\right|.$

Wert von $\boldsymbol{t}$ ermitteln

Um die Betragsstriche aufzulösen, wird eine Fallunterscheidung durchgeführt:

Für $(t^3+1)>0$ gilt:

$\begin{array}[t]{rll} \dfrac{3}{2}&=&\dfrac{1}{6}\cdot(t^3+1) &\quad \scriptsize \mid\; \cdot 6 \\[5pt] 9&=& t^3+1 &\quad \scriptsize \mid\; -1 \\[5pt] 8&=& t^3 &\quad \scriptsize \mid\; \sqrt[3]{\;} \\[5pt] 2&=& t \end{array}$

Für $(t^3+1)\lt0$ gilt:

$\begin{array}[t]{rll} \dfrac{3}{2}&=&\dfrac{1}{6}\cdot(-(t^3+1)) &\quad \scriptsize \mid\; \cdot 6 \\[5pt] 9&=& -t^3-1 &\quad \scriptsize \mid\; +1 \\[5pt] 10&=& -t^3 &\quad \scriptsize \mid\; \cdot (-1)\\[5pt] -10&=& t^3 &\quad \scriptsize \mid\; \sqrt[3]{\;} \\[5pt] -\sqrt[3]{10}&=& t \end{array}$

Das Volumen nimmt folglich für $t_1=2$ und $t_2=-\sqrt[3]{10}$ den Wert $\dfrac{3}{2}$ an.

2.2

Aus den Rechenschritten aus Aufgabe 1.4 geht hervor, dass die Grundfläche ihren minimalen Flächeninhalt bei $t=0,5$ besitzt.

Das Volumen der Pyramide ist genau dann minimal, wenn die vier Punkte, d.h. die Spitze und die Punkte, die die Grundfläche bilden, in einer Ebene liegen. Dort nimmt sie das Volumen $V=0$ an.

Es soll also gelten:

$\begin{array}[t]{rll} V(t)&=& 0 & \\[5pt] \dfrac{1}{6}\cdot\left|(t^3+1)\right|&=& 0 &\quad \scriptsize \mid\; \cdot 6\\[5pt] t^3+1&=& 0 & \quad \scriptsize \mid\; -1 \\[5pt] t^3&=& -1 & \quad \scriptsize \mid\; \sqrt[3]{\;} \\[5pt] t&=& -1 \end{array}$

Da der Flächeninhalt jedoch bei $t=0,5$ minimal ist, ist die Pyramide mit minimaler Grundfläche nicht gleichzeitig die Pyramide mit minimalem Volumen.