B1 - Analytische Geometrie
1
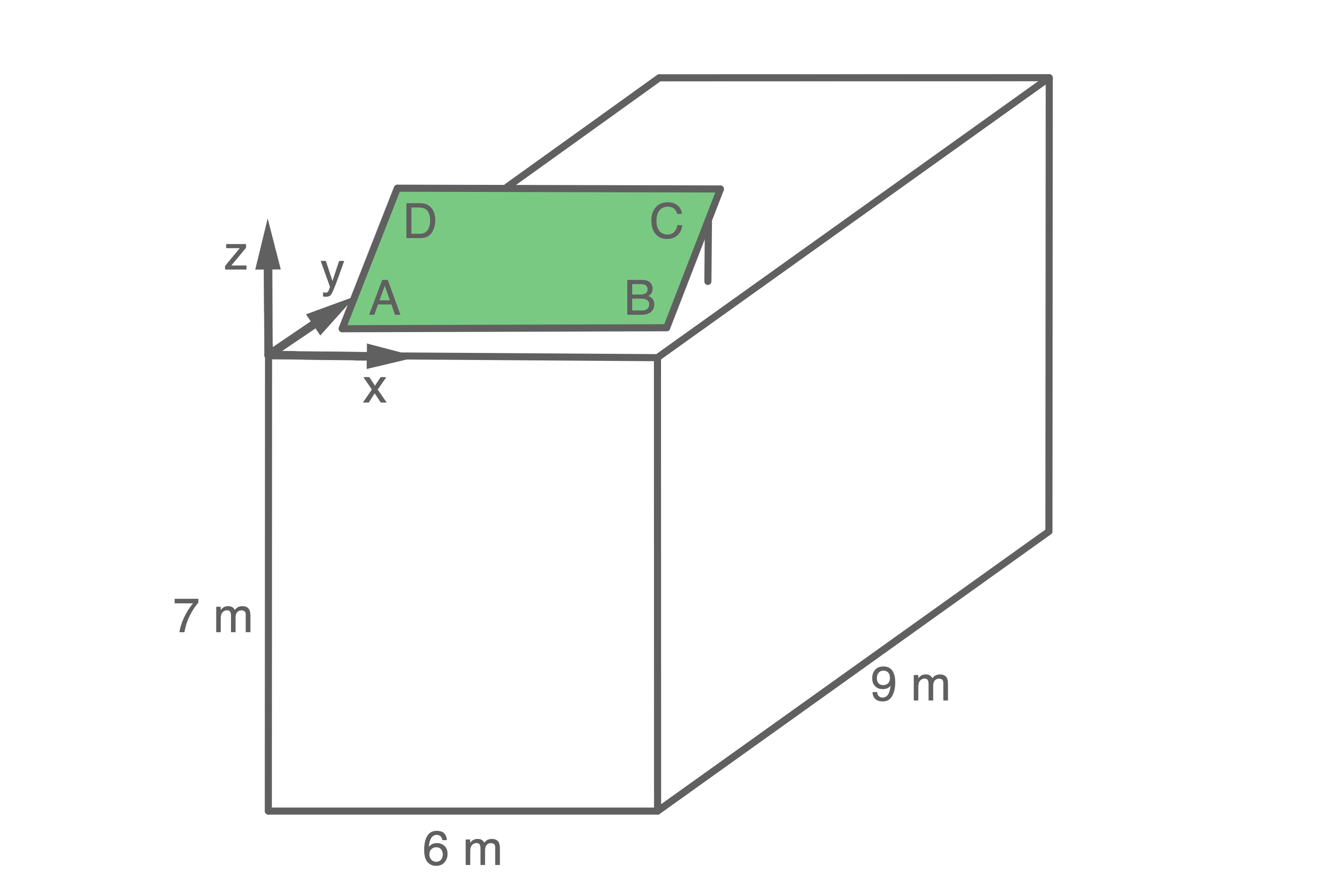
Das Dach eines quaderförmigen Gebäudes soll mit Solarkollektoren versehen werden. Die in der  -
- -Ebene gelegene Seitenfläche des Gebäudes weist dabei genau nach Süden.
Zur Vereinfachung der folgenden Berechnungen wird im Modell die Dachfläche des Gebäudes in die
-Ebene gelegene Seitenfläche des Gebäudes weist dabei genau nach Süden.
Zur Vereinfachung der folgenden Berechnungen wird im Modell die Dachfläche des Gebäudes in die  -
- -Ebene gelegt. Die Kollektorfläche der Solaranlage wird dann in dem vorgegebenen Koordinatensystem der folgenden Abbildung durch die Eckpunkte
-Ebene gelegt. Die Kollektorfläche der Solaranlage wird dann in dem vorgegebenen Koordinatensystem der folgenden Abbildung durch die Eckpunkte  ,
,  ,
,  und
und  beschrieben (alle Angaben in Metern).
beschrieben (alle Angaben in Metern).

1.1
Zeige rechnerisch, dass es sich bei dem Viereck  um ein Rechteck handelt, und prüfe, ob der für eine Kollektorfläche geforderte Mindestflächeninhalt von
um ein Rechteck handelt, und prüfe, ob der für eine Kollektorfläche geforderte Mindestflächeninhalt von  unterschritten wird.
unterschritten wird.
(4 BE)
1.2
Die Solaranlage arbeitet mit der größtmöglichen Leistung, wenn die Sonnenstrahlen senkrecht auf die Kollektorfläche treffen.
Berechne die Richtung, in der die Sonnenstrahlen in diesem Fall auftreffen.
Berechne die Richtung, in der die Sonnenstrahlen in diesem Fall auftreffen.
(4 BE)
1.3
Der Hersteller empfiehlt für die Kollektoren aus Gründen der Standfestigkeit, einen Neigungswinkel  von
von  gegenüber der Dachfläche nicht zu überschreiten. Untersuche, ob dieses Kriterium für die geplante Anlage erfüllt ist.
gegenüber der Dachfläche nicht zu überschreiten. Untersuche, ob dieses Kriterium für die geplante Anlage erfüllt ist.
(3 BE)
2
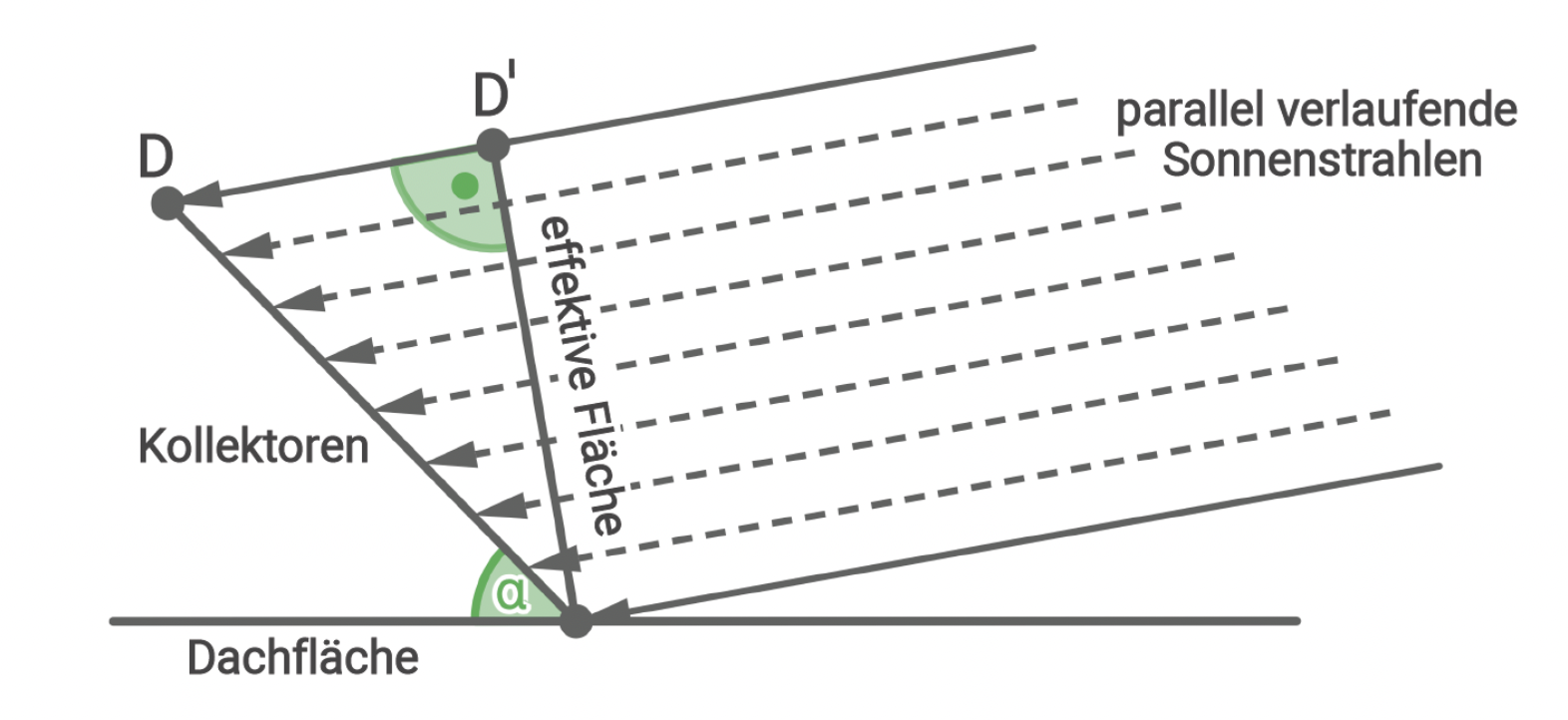
Treffen die Sonnenstrahlen nicht orthogonal auf die Kollektorfläche, so ist die Leistung der Anlage reduziert. Dies wird berücksichtigt, indem man von einer reduzierten Kollektorfläche ausgeht, die als effektive Kollektorfläche  bezeichnet wird. Die Leistung der Anlage ist proportional zum Flächeninhalt der effektiven Kollektorfläche.
Die Abbildung zeigt die Lage der effektiven Fläche im Vergleich zur tatsächlichen Position der Kollektoren (Blickrichtung parallel zur
bezeichnet wird. Die Leistung der Anlage ist proportional zum Flächeninhalt der effektiven Kollektorfläche.
Die Abbildung zeigt die Lage der effektiven Fläche im Vergleich zur tatsächlichen Position der Kollektoren (Blickrichtung parallel zur  -Achse). Es ist ersichtlich, dass die Eckpunkte
-Achse). Es ist ersichtlich, dass die Eckpunkte  und
und  ebenfalls Eckpunkte der effektiven Kollektorfläche sind.
ebenfalls Eckpunkte der effektiven Kollektorfläche sind.

2.1
Um die Effektivität der Solaranlage abzuschätzen, soll die Fläche  für einen ungünstigen Sonnenstand berechnet werden, bei dem die Sonnenstrahlen durch den Vektor
für einen ungünstigen Sonnenstand berechnet werden, bei dem die Sonnenstrahlen durch den Vektor  angegeben werden können.
Berechne die Lage des im Material 2 eingezeichneten Punktes
angegeben werden können.
Berechne die Lage des im Material 2 eingezeichneten Punktes  .
.

(7 BE)
2.2
Bestimme den Flächeninhalt der effektiven Kollektorfläche für den in Aufgabe 2.1 beschriebenen Fall und ermittle, wie viel Prozent der maximalen Leistung bei diesem Sonnenstand erzielt werden können.
(2 BE)
3
Um zu überprüfen, ob weitere Kollektoren auf dem Dach aufgestellt werden können, ohne dass diese durch die bereits bestehenden Kollektoren beschattet werden, soll für den in Aufgabe 2.1 beschriebenen Sonnenstand der Schatten der Kollektorfläche  auf der Dachfläche betrachtet werden.
auf der Dachfläche betrachtet werden.
3.1
Für beliebige Punkte  können die Schattenpunkte auf der Dachfläche für den in Aufgabe 2.1 beschriebenen Sonnenstand durch eine Projektion in Richtung
können die Schattenpunkte auf der Dachfläche für den in Aufgabe 2.1 beschriebenen Sonnenstand durch eine Projektion in Richtung  in die
in die  -
- -Ebene ermittelt werden.
-Ebene ermittelt werden.
Bestimme die Matrix, die diese Projektion beschreibt.
Bestimme die Matrix, die diese Projektion beschreibt.
(7P)
3.2
Berechne mithilfe deines Ergebnisses aus Aufgabe 3.1 die Schattenpunkte der Eckpunkte der Kollektorfläche auf der Dachfläche, und entscheide, ob der Schatten ganz auf der Dachfläche liegt.
Falls du in Aufgabe 3.1 keine Lösung gefunden hast, verwende die Matrix
 .
.
Falls du in Aufgabe 3.1 keine Lösung gefunden hast, verwende die Matrix
(3BE)
1
1.1
Rechteck nachweisen
Das Viereck  ist genau dann ein Rechteck, wenn die jeweils gegenüberliegenden Seiten gleich lang sind, parallel zueinander sind und die anliegenden Seiten senkrecht aufeinander stehen.
Die Verbindungsvektoren der Eckpunkte müssen also folgende Bedingungen erfüllen:
ist genau dann ein Rechteck, wenn die jeweils gegenüberliegenden Seiten gleich lang sind, parallel zueinander sind und die anliegenden Seiten senkrecht aufeinander stehen.
Die Verbindungsvektoren der Eckpunkte müssen also folgende Bedingungen erfüllen:
![\(\begin{array}[t]{rll}
\overrightarrow{AD}&=& \overrightarrow{OD}-\overrightarrow{OA}& \\[5pt]
&=& \pmatrix{0,5\\2,8\\2,1}- \pmatrix{0,5\\1\\0} & \\[5pt]
&=& \left(\begin{array}{c}0\\1,8\\2,1\end{array}\right)& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e225787dbad2e69ec26f72ebdfe6b39bb445a2052bdbd0c6b36494b9400f6092_light.svg)
![\(\begin{array}[t]{rll}
\overrightarrow{BC}&=&\overrightarrow{OC}-\overrightarrow{OB} & \\[5pt]
&=& \left(\begin{array}{c}5,5\\2,8\\2,1\end{array}\right) - \left(\begin{array}{c}5,5\\1\\0\end{array}\right) & \\[5pt]
&=&\left(\begin{array}{c}0\\1,8\\2,1\end{array}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/986daf817dbc943ff33d0f94caf01bc9b0d26015d485d95f1a6e06fe8cf1fe3c_light.svg)
![\(\begin{array}[t]{rll}
\overrightarrow{AB}&=& \overrightarrow{OB}-\overrightarrow{OA}& \\[5pt]
&=& \left(\begin{array}{c}5,5\\1\\0\end{array}\right)- \pmatrix{0,5\\1\\0}& \\[5pt]
&=& \pmatrix{5\\0\\0}
\end{array}\)](https://www.schullv.de/resources/formulas/47d621a702618e490de90125a31e49d1eccf32d520833d691a9861560662b977_light.svg)
![\(\begin{array}[t]{rll}
\overrightarrow{DC}&=& \overrightarrow{OC}-\overrightarrow{OD}& \\[5pt]
&=& \left(\begin{array}{c}5,5\\2,8\\2,1\end{array}\right)- \pmatrix{0,5\\2,8\\2,1}& \\[5pt]
&=& \pmatrix{5\\0\\0}
\end{array}\)](https://www.schullv.de/resources/formulas/9fa866458825f68ad9ecd665296128c33fc1db950888b7fab052eb20da10dd5f_light.svg) 2. Schritt: Orthogonalität zeigen
Es reicht zu zeigen, dass
2. Schritt: Orthogonalität zeigen
Es reicht zu zeigen, dass  und
und  senkrecht aufeinander stehen, da wir bereits
senkrecht aufeinander stehen, da wir bereits  und
und  gezeigt haben.
gezeigt haben.
![\(\begin{array}[t]{rll}
\overrightarrow{AD} \circ \overrightarrow{AB}&=& \begin{pmatrix}0\\ 1,8\\ 2,1\end{pmatrix} \circ \begin{pmatrix}5\\ 0\\ 0\end{pmatrix} & \\[5pt]
&=& 0 \cdot 5 + 1,8 \cdot 0 + 2,1 \cdot 0& \\[5pt]
&=& 0 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/212bb2404106c5ab8a8a4474e5439b7180853024d2d6e344974d43d148e0dacc_light.svg) Damit ist gezeigt, dass das Viereck
Damit ist gezeigt, dass das Viereck  ein Rechteck ist.
Flächeninhalt
ein Rechteck ist.
Flächeninhalt  prüfen
Der geforderte Mindestflächeninhalt von
prüfen
Der geforderte Mindestflächeninhalt von  wird folglich nicht unterschritten.
wird folglich nicht unterschritten.
und
1.2
Die Richtung, in der die Sonnenstrahlen senkrecht auf die Kollektorfläche treffen, ist durch die Normalenvektoren der Ebene, welche durch die Vektoren  und
und  aufgespannt wird, gegeben.
Ein solcher Normalenvektor
aufgespannt wird, gegeben.
Ein solcher Normalenvektor  kann mit Hilfe des Vektorprodukts bestimmt werden:
kann mit Hilfe des Vektorprodukts bestimmt werden:
![\(\begin{array}[t]{rll}
\overrightarrow{n}&=&\overrightarrow{AB}\times\overrightarrow{AD} & \\[5pt]
&=& \left(\begin{array}{c}5\\0\\0\end{array}\right) \times \left(\begin{array}{c}0\\1,8\\2,1\end{array}\right)& \\[5pt]
&=& \left(\begin{array}{c}0-0\\0 -2,1 \cdot 5\\5 \cdot 1,8 - 0\end{array}\right)& \\[5pt]
&=&\left(\begin{array}{c}0\\-10,5\\9\end{array}\right)
\end{array}\)](https://www.schullv.de/resources/formulas/5334a9c95d2e97f9626e8801666567260816d7ec4742e3a0418c7fdda14e87bc_light.svg) Da die Sonnenstrahlen von oben auf die Kollektorfläche auftreffen, muss der Vektor also nach unten zeigen. Die
Da die Sonnenstrahlen von oben auf die Kollektorfläche auftreffen, muss der Vektor also nach unten zeigen. Die  -Koordinate muss folglich negativ sein.
Durch Umkehren der Vorzeichen erhält man also:
-Koordinate muss folglich negativ sein.
Durch Umkehren der Vorzeichen erhält man also:
 Somit treffen die Sonnenstrahlen in der Richtung
Somit treffen die Sonnenstrahlen in der Richtung  senkrecht auf die Kollektorfläche auf.
senkrecht auf die Kollektorfläche auf.
1.3
Der Neigungswinkel der Kollektorfläche gegenüber dem Dach entspricht dem Winkel zwischen dem Vektor  und der
und der  -Achse. Der Richtungsvektor der
-Achse. Der Richtungsvektor der  -Achse ist durch
-Achse ist durch  gegeben.
Mit der Formel für Schnittwinkel folgt:
gegeben.
Mit der Formel für Schnittwinkel folgt:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\left| \overrightarrow{AD} \circ \left(\begin{array}{c}0\\1\\0\end{array}\right) \right|}{ \left| \overrightarrow{AD} \right| \cdot \left|\left(\begin{array}{c}0\\1\\0\end{array}\right) \right|} & \\[5pt]
\cos(\alpha)&=& \dfrac{\left| \left(\begin{array}{c}0\\1,8\\2,1\end{array}\right) \circ \left(\begin{array}{c}0\\1\\0\end{array}\right) \right|}{ \left|\left(\begin{array}{c}0\\1,8\\2,1\end{array}\right) \right| \cdot \left|\left(\begin{array}{c}0\\1\\0\end{array}\right) \right|}& \\[5pt]
\cos(\alpha)&=& \dfrac{1,8}{\sqrt{7,65} \cdot 1} & \\[5pt]
\cos(\alpha)&\approx& 0,65 &\quad \scriptsize \mid \arccos \\[5pt]
\alpha&\approx& 49,46
\end{array}\)](https://www.schullv.de/resources/formulas/c6e17b638903716f77c698b2ae2ecf796b092f29261c4ceb8a82823373f4186c_light.svg) Der Neigungswinkel beträgt somit etwa
Der Neigungswinkel beträgt somit etwa  und überschreitet folglich die empfohlene Grenze von
und überschreitet folglich die empfohlene Grenze von  nicht.
nicht.
2
2.1
Aus dem Material 2 können folgende Bedingungen für die Lage des Punktes  abgelesen werden:
Der Punkt
abgelesen werden:
Der Punkt  kann durch den dazugehörigen Ortsvektor
kann durch den dazugehörigen Ortsvektor  definiert werden.
1. Schritt: Gleichungssystem zu
definiert werden.
1. Schritt: Gleichungssystem zu  aufstellen
Der Verbindungsvektor
aufstellen
Der Verbindungsvektor  ist gegeben durch:
ist gegeben durch:
 Die erste Bedingung kann nun wie folgt in ein Gleichungssystem umgeschrieben und gelöst werden:
Aus
Die erste Bedingung kann nun wie folgt in ein Gleichungssystem umgeschrieben und gelöst werden:
Aus  kann direkt
kann direkt  abgelesen werden.
Durch Einsetzen von
abgelesen werden.
Durch Einsetzen von  in
in  ergibt sich:
Damit gilt für den Ortsvektor des Punktes
ergibt sich:
Damit gilt für den Ortsvektor des Punktes  :
:  2. Schritt: Gleichung zu
2. Schritt: Gleichung zu  aufstellen
Für den Verbindungsvektor
aufstellen
Für den Verbindungsvektor  gilt:
gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{AD‘}&=&\overrightarrow{OD‘}-\overrightarrow{OA} & \\[5pt]
&=& \begin{pmatrix}0,5 - 0,5\\ \left(10,3- \frac{25}{7}\cdot d_3 \right) -1\\ d_3 - 0 \end{pmatrix}& \\[5pt]
&=&\begin{pmatrix}0\\ 9,3- \frac{25}{7}\cdot d_3 \\ d_3 \end{pmatrix}
\end{array}\)](https://www.schullv.de/resources/formulas/c00c60c63bd4c5446c125c605993ade4704c2b6b1770e55ccb0853ca53b11798_light.svg) Die zweite Bedingung kann nun wie folgt als Gleichung formuliert und gelöst werden:
Durch Einsetzen in die Koordinaten von
Die zweite Bedingung kann nun wie folgt als Gleichung formuliert und gelöst werden:
Durch Einsetzen in die Koordinaten von  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
d_2&=& 10,3- \dfrac{25}{7} \cdot d_3& \\[5pt]
&=& 10,3- \dfrac{25}{7} \cdot \dfrac{3.255}{1.348}& \\[5pt]
&\approx& 1,68 & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6563d005e28e43c0b4f4d9fd6edd7da13e223da2f7b476372fbd8efefba4890c_light.svg) Der gesuchte Punkt ist somit
Der gesuchte Punkt ist somit 
2.2
Flächeninhalt  bestimmen
bestimmen
![\(\begin{array}[t]{rll}
F_{eff}&=& \left|\overrightarrow{AD‘}\right| \cdot \left|\overrightarrow{AB}\right|&\\[5pt]
&=& \left|\begin{pmatrix}0\\ 0,68\\ 2,41 \end{pmatrix} \right| \cdot \left| \begin{pmatrix}5\\ 0\\ 0\\ \end{pmatrix}\right|&\\[5pt]
&=&\sqrt{0,68^2+2,41^2} \cdot 5 &\\[5pt]
&\approx& 12,52\; [\,\text{m}^2]&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c7e29c397b3244da82a65fac037e1ca80d1674f2a913b16d52088a45231e93e8_light.svg) In dem in Aufgabe 2.1 beschriebenen Fall ist der Flächeninhalt der effizienten Kollektorfläche folglich
In dem in Aufgabe 2.1 beschriebenen Fall ist der Flächeninhalt der effizienten Kollektorfläche folglich  .
Prozentsatz der maximalen Leistung bestimmen
Die maximale Leistung wird genau dann erreicht, wenn die Sonnenstrahlen senkrecht auf der Kollektorfläche stehen. Die Leistung ist hierbei proportional zum Flächeninhalt der Kollektorfläche.
Den gesuchte Prozentsatz
.
Prozentsatz der maximalen Leistung bestimmen
Die maximale Leistung wird genau dann erreicht, wenn die Sonnenstrahlen senkrecht auf der Kollektorfläche stehen. Die Leistung ist hierbei proportional zum Flächeninhalt der Kollektorfläche.
Den gesuchte Prozentsatz  kann also anhand von den Flächeninhalten
kann also anhand von den Flächeninhalten  und
und  ermittelt werden:
ermittelt werden:
 In dem in Aufgabe 2.1 beschriebenen Fall kann also
In dem in Aufgabe 2.1 beschriebenen Fall kann also  der maximalen Leistung erzielt werden.
der maximalen Leistung erzielt werden.
3
3.1
Da nach eine Projektionsmatrix  gesucht ist, welche beliebige Punkte
gesucht ist, welche beliebige Punkte  in die
in die  -Ebene projiziert,muss für einen beliebigen Punkt
-Ebene projiziert,muss für einen beliebigen Punkt  mit Schattenpunkt
mit Schattenpunkt  also gelten:
also gelten:
 .
Der Schattenpunkt eines beliebigen Punktes
.
Der Schattenpunkt eines beliebigen Punktes  entspricht dem Schnittpunkt der
entspricht dem Schnittpunkt der  -Ebene mit der Geraden
-Ebene mit der Geraden  eines Sonnenstrahls durch den Punkt
eines Sonnenstrahls durch den Punkt  .
1. Schritt: Allgemeinen Schattenpunkt
.
1. Schritt: Allgemeinen Schattenpunkt  berechnen
Die
berechnen
Die  -
- -Ebene ist gegeben durch die Ebenengleichung
-Ebene ist gegeben durch die Ebenengleichung  .
Durch Gleichsetzen der Geraden- und die Ebenengleichung folgt:
Es kann direkt
.
Durch Gleichsetzen der Geraden- und die Ebenengleichung folgt:
Es kann direkt  abgelesen werden. Die
abgelesen werden. Die  -Koordinate bleibt also durch die Projektion unverändert.
Aus der dritten Zeile ergibt sich folgende Gleichung:
-Koordinate bleibt also durch die Projektion unverändert.
Aus der dritten Zeile ergibt sich folgende Gleichung:
![\(\begin{array}[t]{rll}
z+\lambda \cdot \left(-7\right)&=&0 &\quad\scriptsize \mid\; -z \\[5pt]
\lambda \cdot \left(-7\right)&=&-z&\quad\scriptsize \mid\; :(-7) \\[5pt]
\lambda&=& \dfrac{z}{7}
\end{array}\)](https://www.schullv.de/resources/formulas/a3d7b211efdf430728ed7720bf27d4b47f51c4e3038bc2dcdd356cda9de6c7a8_light.svg) Durch Einsetzen von
Durch Einsetzen von  in die Gleichung für die
in die Gleichung für die  -Koordinate folgt:
-Koordinate folgt:
![\(\begin{array}{rll}
y+\lambda \cdot 25 &=& b &\quad\scriptsize \mid\; \lambda=\dfrac{z}{7}\\[5pt]
y + z \cdot \dfrac{25}{7} &=&b \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/ed9c0a7e6970c21ce2bbcb170261bc6a34a1cda06d7a8b569d66050230389392_light.svg) Damit gilt für einen Schattenpunkt
Damit gilt für einen Schattenpunkt  eines beliebigen Punktes
eines beliebigen Punktes  :
:
 2. Schritt: Projektionsmatrix
2. Schritt: Projektionsmatrix  bestimmen
Durch Einsetzen des oben berechneten Schnittpunkt in die Bedingung für die Projektionsmatrix
bestimmen
Durch Einsetzen des oben berechneten Schnittpunkt in die Bedingung für die Projektionsmatrix  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
\begin{pmatrix}a\\ b\\ 0\end{pmatrix}&=& \begin{pmatrix}x\\ y + z \cdot \frac{25}{7}\\ 0 \end{pmatrix}&\\[5pt]
&=&\begin{pmatrix}1\cdot x+0\cdot y+0\cdot z\\ 0\cdot x+1\cdot y+\frac{25}{7}\cdot z\\ 0\cdot x+0\cdot y+0\cdot z\\ \end{pmatrix} &\\[5pt]
&=& \begin{pmatrix}1&0&0\\ 0&1&\frac{25}{7}\\ 0&0&0\\ \end{pmatrix} \cdot \begin{pmatrix}x\\ y\\ z\end{pmatrix}&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bf22b522c7d035f2903ad7aaf773b851587d17ae603f71719b84b89b53e1207e_light.svg) Somit hat die gesuchte Projektionsmatrix
Somit hat die gesuchte Projektionsmatrix  die Form:
die Form:

3.2
Schattenpunkte berechnen
Die Schattenpunkte der Eckpunkte können mit dem Matrix-Vektor-Produkt der Projektionsmatrix  und den Ortsvektoren der Eckpunkte bestimmt werden.
Da
und den Ortsvektoren der Eckpunkte bestimmt werden.
Da  und
und  keine Schatten werfen, weil sie bereits auf dem Dach liegen, reicht es, die Punkte
keine Schatten werfen, weil sie bereits auf dem Dach liegen, reicht es, die Punkte  und
und  zu betrachten.
zu betrachten.
![\(\begin{array}[t]{rll}
\overrightarrow{OC_S}&=&M \cdot \overrightarrow{OC} \\[5pt]
&=& \begin{pmatrix}1&0&0\\ 0&1&\frac{25}{7}\\ 0&0&0\\ \end{pmatrix} \cdot \begin{pmatrix}5,5\\ 2,8\\ 2,1\end{pmatrix} & \\[5pt]
&=& \begin{pmatrix}5,5\\ 2,8 + 2,1 \cdot \frac{25}{7}\\ 0\end{pmatrix} & \\[5pt]
&=& \begin{pmatrix}5,5\\ 10,3\\ 0\end{pmatrix} & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5562d0a5430c3af134ef0158ca6b069deb41b648be59a5a8329fb8d41a1c372d_light.svg)
![\(\begin{array}[t]{rll}
\overrightarrow{OD_S}&=&M \cdot \overrightarrow{OD} & \\[5pt]
&=& \begin{pmatrix}1&0&0\\ 0&1&\frac{25}{7}\\ 0&0&0\\ \end{pmatrix} \cdot \begin{pmatrix}0,5\\ 2,8\\ 2,1\end{pmatrix} & \\[5pt]
&=&\begin{pmatrix}0,5\\ 10,3\\0 \end{pmatrix}
\end{array}\)](https://www.schullv.de/resources/formulas/bdf5cb9839ef81d9fe4fffc04f13319ef006b4fda0600e423ae5b9639eedc3dd_light.svg) Damit sind
Damit sind  und
und  die Schattenpunkte von
die Schattenpunkte von  und
und  .
Entscheidung treffen
Die Dachfläche ist in
.
Entscheidung treffen
Die Dachfläche ist in  -Richtung 9 Meter lang. Die Schattenpunkte haben jedoch einen
-Richtung 9 Meter lang. Die Schattenpunkte haben jedoch einen  -Wert von 10,3 und liegen somit hinter dem Ende des Daches. Der Schatten liegt folglich nicht ganz auf der Dachfläche.
-Wert von 10,3 und liegen somit hinter dem Ende des Daches. Der Schatten liegt folglich nicht ganz auf der Dachfläche.