C1 - Stochastik
Im Kampf gegen Doping sollten bei den Olympischen Sommerspielen in London mit neuen Verfahren "saubere Spiele" gewährleistet werden. Es sollten 5000 Tests durchgeführt werden.
Ein Mediziner äußert Zweifel, da weltweit pro Jahr ca. 300000 Dopingtests durchgeführt würden, davon nur  mit positivem Ergebnis. Dies stehe im Widerspruch zu Studien, bei denen ein wesentlich größerer Anteil der Nachwuchssportler Doping zugaben.
mit positivem Ergebnis. Dies stehe im Widerspruch zu Studien, bei denen ein wesentlich größerer Anteil der Nachwuchssportler Doping zugaben.

 für
für 
1.1
Es kann angenommen werden, dass es sich bei den geplanten Dopingtests bei den Olympischen Sommerspielen in London um Bernoulli-Experimente handelt.
Gib eine Definition der Zufallsvariablen  an und nenne die Bedingungen, unter denen
an und nenne die Bedingungen, unter denen  als binomialverteilt angenommen werden kann.
als binomialverteilt angenommen werden kann.
(3 BE)
1.2
Beschreibe die Bedeutung der folgenden Rechnung im Sachzusammenhang:

(3 BE)
2
Mit neuem Verfahren verspricht ein renommiertes französisches Labor, die Quote der Dopingtests mit positivem Ergebnis von  auf
auf  zu erhöhen.
In einem ersten Test unter 1000 Teilnehmern der Leichtathletik Jugendweltmeisterschaften wurden 6 Sportlerinnen und Sportler des Dopings überführt. Ein Heidelberger Molekularbiologe hält die Euphorie für verfrüht. Beide Seiten versuchen ihre Sichtweise durch ein Testverfahren zu untermauern.
zu erhöhen.
In einem ersten Test unter 1000 Teilnehmern der Leichtathletik Jugendweltmeisterschaften wurden 6 Sportlerinnen und Sportler des Dopings überführt. Ein Heidelberger Molekularbiologe hält die Euphorie für verfrüht. Beide Seiten versuchen ihre Sichtweise durch ein Testverfahren zu untermauern.
Französisches Labor
Nullhypothese:  Gegenhypothese:
Gegenhypothese:  Signifikanzniveau:
Signifikanzniveau: 
Heidelberger Molekularbiologe
Nullhypothese:  Gegenhypothese:
Gegenhypothese:  Signifikanzniveau:
Signifikanzniveau: 
2.1
Bestimme die jeweiligen Annahmebereiche der Nullhypothese und beurteile anhand des Testergebnisses das neue Testverfahren.
(8 BE)
2.2
Beschreibe an einem der beiden Testverfahren, was in diesem Sachzusammenhang die Fehler 1. und 2. Art sind, und bestimme anschließend für beide Testverfahren den Fehler 2. Art.
Verwende für die Berechnung des Fehlers 2. Art die Wahrscheinlichkeit der Nullhypothese des jeweils anderen Labors.
(6 BE)
3
Ein amerikanischer Dopingexperte machte 2012 eine drastische Aussage in Bezug auf die Olympischen Spiele:
"Etwa  aller Athleten sind gedopt."
Mit Hilfe einer anonymen Umfrage wollen Medizinstudenten herausfinden, wie hoch die Dunkelziffer der gedopten Athleten bei den Olympischen Spielen ist. Dabei soll ein Verfahren verwendet werden, das den Befragten weitgehenden Schutz verspricht.
Der Athlet soll die Frage beantworten:
aller Athleten sind gedopt."
Mit Hilfe einer anonymen Umfrage wollen Medizinstudenten herausfinden, wie hoch die Dunkelziffer der gedopten Athleten bei den Olympischen Spielen ist. Dabei soll ein Verfahren verwendet werden, das den Befragten weitgehenden Schutz verspricht.
Der Athlet soll die Frage beantworten:
"Stimmt es, dass Sie im Wettkampf oder im Training Dopingmittel benutzt haben?" Die Antwort soll er nach folgender Regel geben:
Aus einer Urne mit 4 roten, 2 schwarzen und 3 weißen Kugeln zieht der Athlet zunächst unbeobachtet eine Kugel. Ist sie rot, beantwortet er die Frage mit NEIN, ist sie schwarz, mit JA. Zieht er eine weiße Kugel, so antwortet er wahrheitsgemäß (mit JA oder NEIN). Von 3010 getesteten Athleten antworteten 1093 mit JA.
"Stimmt es, dass Sie im Wettkampf oder im Training Dopingmittel benutzt haben?" Die Antwort soll er nach folgender Regel geben:
Aus einer Urne mit 4 roten, 2 schwarzen und 3 weißen Kugeln zieht der Athlet zunächst unbeobachtet eine Kugel. Ist sie rot, beantwortet er die Frage mit NEIN, ist sie schwarz, mit JA. Zieht er eine weiße Kugel, so antwortet er wahrheitsgemäß (mit JA oder NEIN). Von 3010 getesteten Athleten antworteten 1093 mit JA.
3.1
Stelle das Testverfahren mit Hilfe eines Baumdiagramms dar und ermittle daraus den Anteil an gedopten Athleten.
(5 BE)
3.2
Einige Athleten befürchten, dass sie bei einer Antwort JA eher des Dopings verdächtigt werden könnten als bei NEIN.
Ermittle die Wahrscheinlichkeit, dass der Athlet, der mit JA geantwortet hat, wirklich Dopingmittel benutzt hat. Verwende dabei die in Aufgabe 3.1 ermittelte Wahrscheinlichkeit  Falls Aufgabe 3.1 nicht bearbeitet wurde, kann
Falls Aufgabe 3.1 nicht bearbeitet wurde, kann  gewählt werden.
gewählt werden.
Material
Binomialsummenfunktion
(5 BE)
| p= | 0,01 | 0,003 |
|---|---|---|
| k= | ||
| 0 | 0,0000 | 0,04956 |
| 1 | 0,0005 | 0,19870 |
| 2 | 0,0027 | 0,42285 |
| 3 | 0,0101 | 0,64723 |
| 4 | 0,0287 | 0,81552 |
| 5 | 0,0661 | 0,91639 |
| 6 | 0,1289 | 0,96672 |
| 7 | 0,2189 | 0,98822 |
| 8 | 0,3317 | 0,99626 |
| 9 | 0,4573 | 0,99892 |
| 10 | 0,5830 | 0,99972 |
| 11 | 0,6974 | 0,99993 |
| 12 | 0,7925 | 0,99998 |
| 13 | 0,8656 | 1,00000 |
| 14 | 0,9176 | 1,00000 |
| 15 | 0,9521 | 1,00000 |
| 16 | 0,9736 | 1,00000 |
| 17 | 0,9862 | 1,00000 |
| 18 | 0,9931 | 1,00000 |
| 19 | 0,9967 | 1,00000 |
| 20 | 0,9985 | 1,00000 |
| 21 | 0,9993 | 1,00000 |
| 22 | 0,9997 | 1,00000 |
| 23 | 0,9999 | 1,00000 |
| 24 | 1,0000 | 1,00000 |
| 25 | 1,0000 | 1,00000 |
1.1
Zufallsvariable  definieren
definieren
 beschreibt die Anzahl der positiven Dopingtests.
Bedingungen nennen
beschreibt die Anzahl der positiven Dopingtests.
Bedingungen nennen
- Die Wahrscheinlichkeit eines positiven Dopingtests ist für jeden befragten Spieler gleich.
- Es gibt jeweils nur zwei mögliche Ergebnisse: "Der Test ist positiv" und "Der Test ist negativ".
1.2
2.1
Annahmebereich des französischen Labors berechnen
Wegen  führt das Labor einen linksseitigen Test durch.
führt das Labor einen linksseitigen Test durch.
Also hat der Annahmebereich die folgende Form: Gesucht ist das kleinste
Gesucht ist das kleinste  , für das die Nulhypothese noch angenommen wird. Es muss gelten:
, für das die Nulhypothese noch angenommen wird. Es muss gelten:
 Mit Hilfe der Tabelle im Material folgt:
Mit Hilfe der Tabelle im Material folgt:

 Damit ergibt sich der folgende Annahmebereich zu:
Damit ergibt sich der folgende Annahmebereich zu:
 Annahmebereich des Heidelberger Molekularbiologen berechnen
Wegen
Annahmebereich des Heidelberger Molekularbiologen berechnen
Wegen  führt der Biologe einen rechtsseitigen Test durch.
führt der Biologe einen rechtsseitigen Test durch.
Der Annnahmebereich hat also die folgende Form: Es muss gelten:
Aus der Tabelle lässt sich ablesen:
Es muss gelten:
Aus der Tabelle lässt sich ablesen:
![\(\begin{array}[t]{rll}
P(X\geq7) &=& 1- 0,96672& \\[5pt]
&=& 0,03328 & \\[5pt]
&\lt & 0,04
\end{array}\)](https://www.schullv.de/resources/formulas/66100c1836d3d28fe6982e5cca531e8c9a62ad097207823d251c936454b09575_light.svg)
![\(\begin{array}[t]{rll}
P(X\geq6)&=& 1- 0,91639& \\[5pt]
&=& 0,08361 & \\[5pt]
&\gt& 0,04
\end{array}\)](https://www.schullv.de/resources/formulas/cff436568e71226f8148e9fec8e773a70cc704f64c5c17d90114426f2c553012_light.svg) Damit ergibt sich der Annahmebereich mit:
Damit ergibt sich der Annahmebereich mit:
 Neues Testverfahren beurteilen
Bei dem Ergebnis von 6 positiven Dopingtests würde die Nullhypothese des französischen Labors angenommen werden. Das Labor würde also weiterhin von einer Wahrscheinlichkeit von
Neues Testverfahren beurteilen
Bei dem Ergebnis von 6 positiven Dopingtests würde die Nullhypothese des französischen Labors angenommen werden. Das Labor würde also weiterhin von einer Wahrscheinlichkeit von  ausgehen.
Nach dem Test des Molekularbiologen in Heidelberg würde dessen Nullhypothese angenommen werden, da
ausgehen.
Nach dem Test des Molekularbiologen in Heidelberg würde dessen Nullhypothese angenommen werden, da  im Annahmebereich liegt. Er würde sich also in seiner Vermutung ebenfalls bestätigt sehen, dass die Wahrscheinlichkeit immer noch bei
im Annahmebereich liegt. Er würde sich also in seiner Vermutung ebenfalls bestätigt sehen, dass die Wahrscheinlichkeit immer noch bei  liegt.
Das neue Testverfahren des französischen Labors ist somit nicht aussagekräftig.
liegt.
Das neue Testverfahren des französischen Labors ist somit nicht aussagekräftig.
Also hat der Annahmebereich die folgende Form:
Der Annnahmebereich hat also die folgende Form:
2.2
- Fehler 1. Art: Die Nullhypothese wird fälschlicherweise abgelehnt.
- Fehler 2. Art: Die Nullhypothese wird fälschlicherweise angenommen.
3.1
Baumdiagramm erstellen
 Wahrscheinlichkeit eines Sportlers, Dopingmittel zu nutzen
Wahrscheinlichkeit eines Sportlers, Dopingmittel zu nutzen
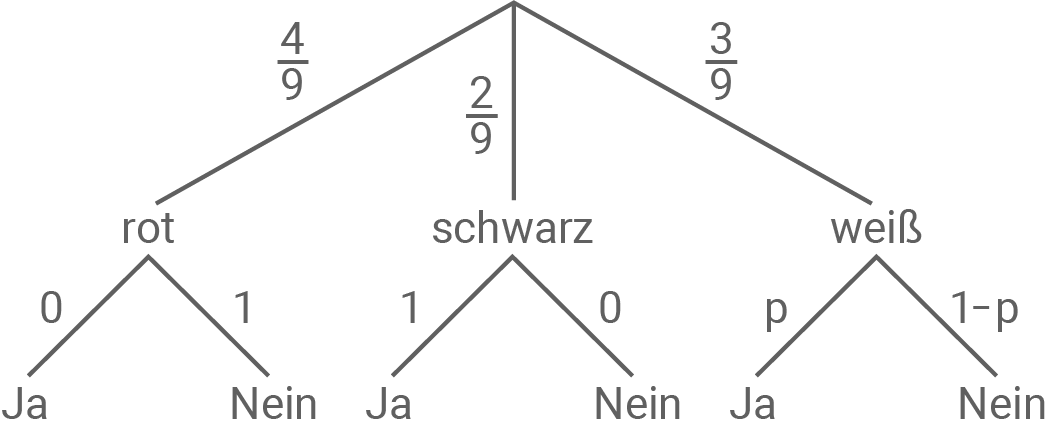 Anteil der gedopten Athleten ermitteln
1093 von 3010 getesteten Athleten haben mit „Ja“ geantwortet.
Es gilt also:
Der Anteil an gedopten Athleten beträgt also ca.
Anteil der gedopten Athleten ermitteln
1093 von 3010 getesteten Athleten haben mit „Ja“ geantwortet.
Es gilt also:
Der Anteil an gedopten Athleten beträgt also ca. 

3.2
- Der gedopte Spieler hat eine schwarze Kugel aus der Urne gezogen
- Der gedopte Spieler hat eine weiße Kugel aus der Urne gezogen