Pflichtteil A1
1.
Kreuze das richtige Ergebnis an.

(1 Pkt.)
2.
In ein Glas passt genau  Liter.
Liter.
Wie viele von diesen Gläsern kann man mit dem Inhalt der drei Flaschen füllen?

Wie viele von diesen Gläsern kann man mit dem Inhalt der drei Flaschen füllen?

(1 Pkt.)
3.
Berechne und gib das Ergebnis mit einer 10er-Potenz an.

(1 Pkt.)
4.
Schlussverkauf – alles um  reduziert. Stimmt diese Aussage?
reduziert. Stimmt diese Aussage?
Begründe rechnerisch.

Begründe rechnerisch.

(1 Pkt.)
5.
Löse die Gleichung.

(1 Pkt.)
6.
Das Netz gehört zum abgebildeten Quader.
Zeichne in das Quadernetz die beiden Diagonalen ein.
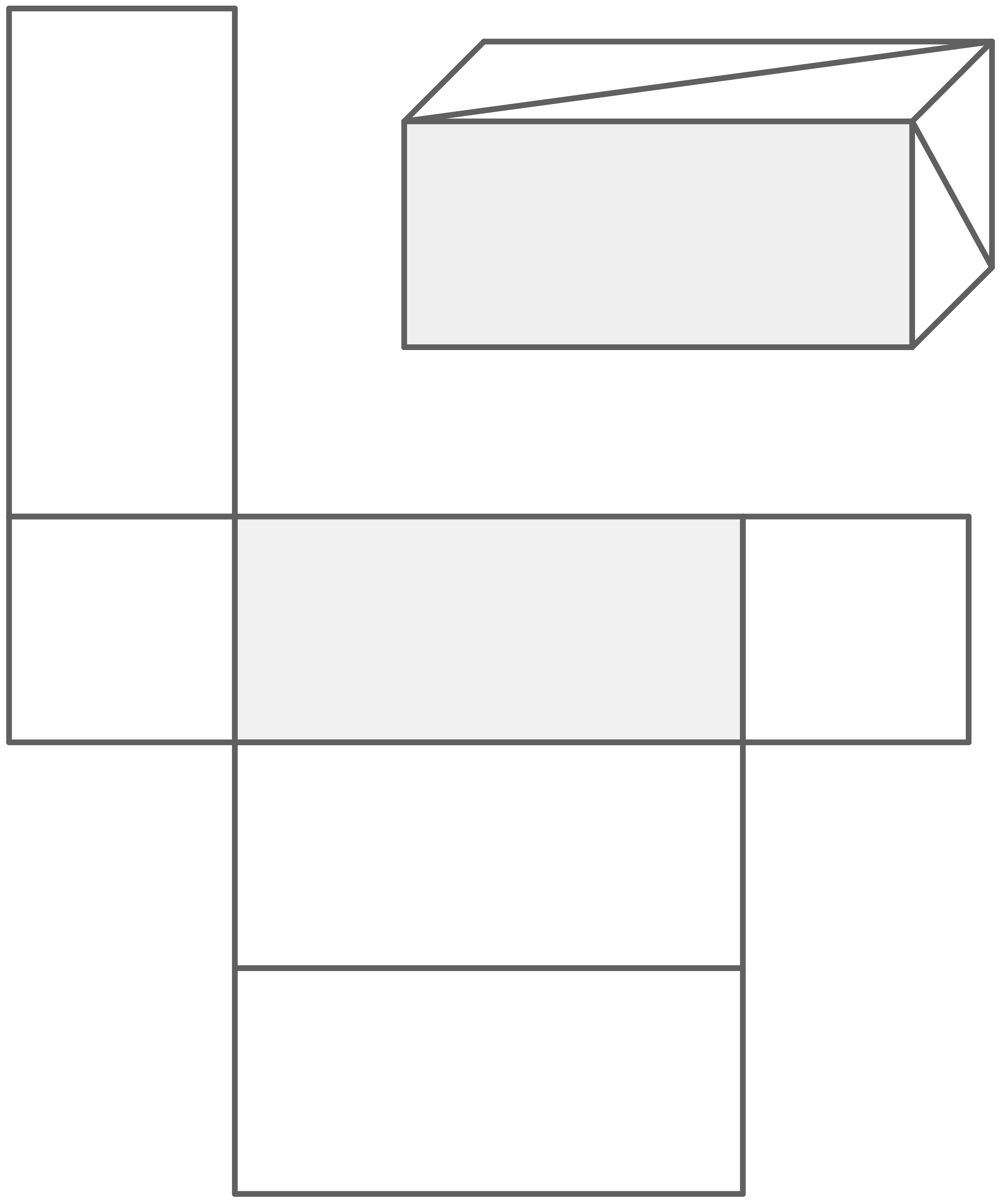
Zeichne in das Quadernetz die beiden Diagonalen ein.

(1 Pkt.)
7.
Haben alle Parallelogramme denselben Flächeninhalt?
Begründe deine Antwort.

Begründe deine Antwort.

(1 Pkt.)
8.
Im letzten Zeugnis hatten die Schülerinnen und Schüler der Klasse 9b folgende Noten in Mathematik.
Berechne den Durchschnitt.
| Note 1 | Note 2 | Note 3 | Note 4 | Note 5 | Note 6 |
|---|---|---|---|---|---|
(1 Pkt.)
9.
Von 50 Gummibärchen sind 25 rot, 10 grün und 15 gelb.
Zeichne die prozentuale Verteilung als Balken in das Schaubild ein.
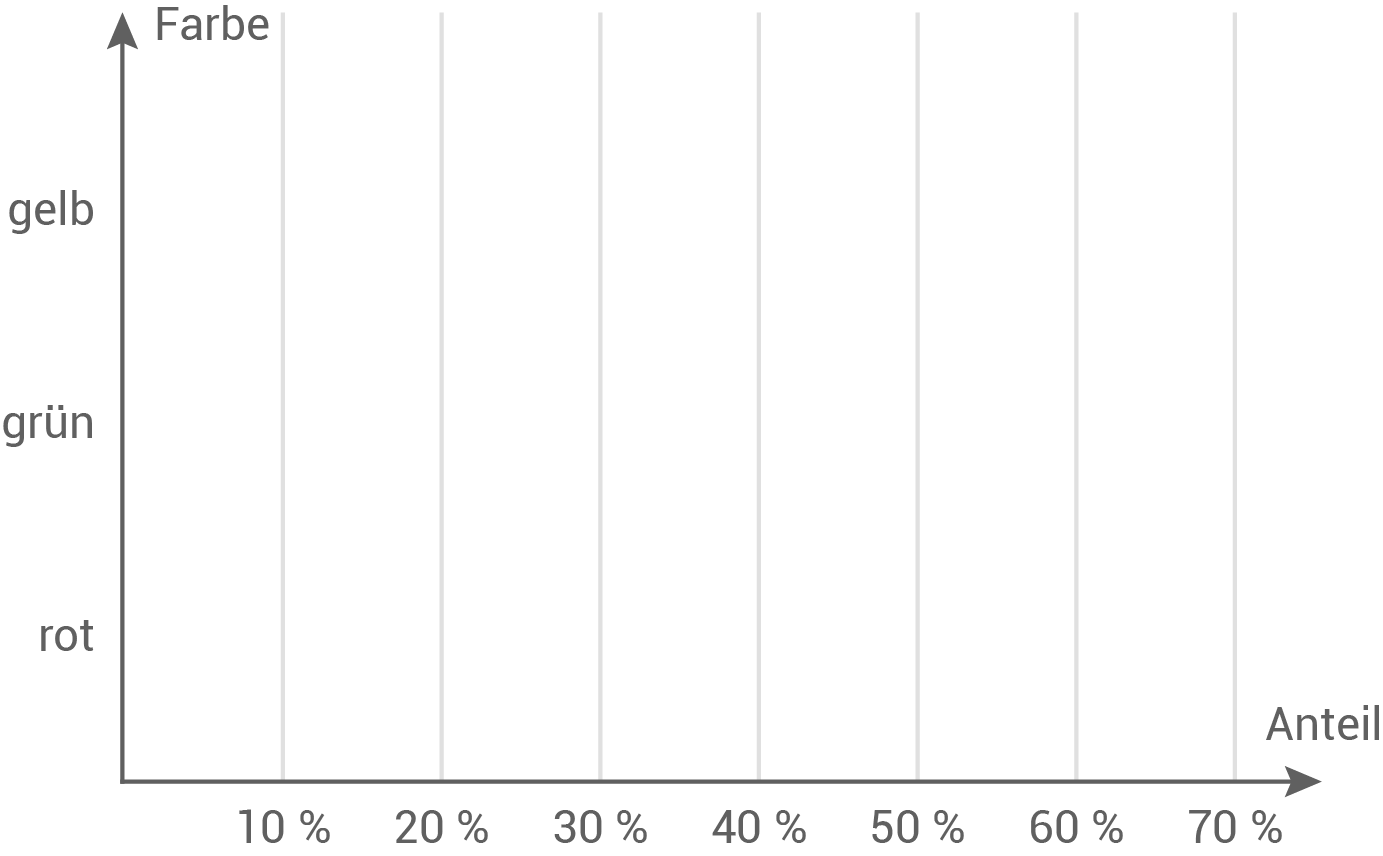
Zeichne die prozentuale Verteilung als Balken in das Schaubild ein.

(1 Pkt.)
10.
Ergänze die fehlenden Werte der proportionalen Zuordnung.
| Gewicht in g | 20 | 30 | |
|---|---|---|---|
| Anzahl der Schrauben | 120 | 240 |
(1 Pkt.)
1.
2.
1. Schritt: Berechnen, wie viel Liter in den drei Flaschen sind
 sind
sind  Somit sind in den drei Flaschen
Somit sind in den drei Flaschen  2. Schritt: Berechnen, in wie viele Gläser
2. Schritt: Berechnen, in wie viele Gläser  passen
passen
 30 Gläser können also mit dem Inhalt der drei Flaschen gefüllt werden.
30 Gläser können also mit dem Inhalt der drei Flaschen gefüllt werden.
3.
4.
Da die Schuhe um  reduziert wurden, müssten sie nur noch
reduziert wurden, müssten sie nur noch  des ursprünglichen Preises kosten.
des ursprünglichen Preises kosten.
 entsprechen
entsprechen 
 von
von  sind:
sind:  Die Aussage stimmt also nicht, denn der neue Preis für die Schuhe müsste nach der Reduzierung nur noch
Die Aussage stimmt also nicht, denn der neue Preis für die Schuhe müsste nach der Reduzierung nur noch  betragen und nicht
betragen und nicht 
5.
6.
Mögliche Lösungen
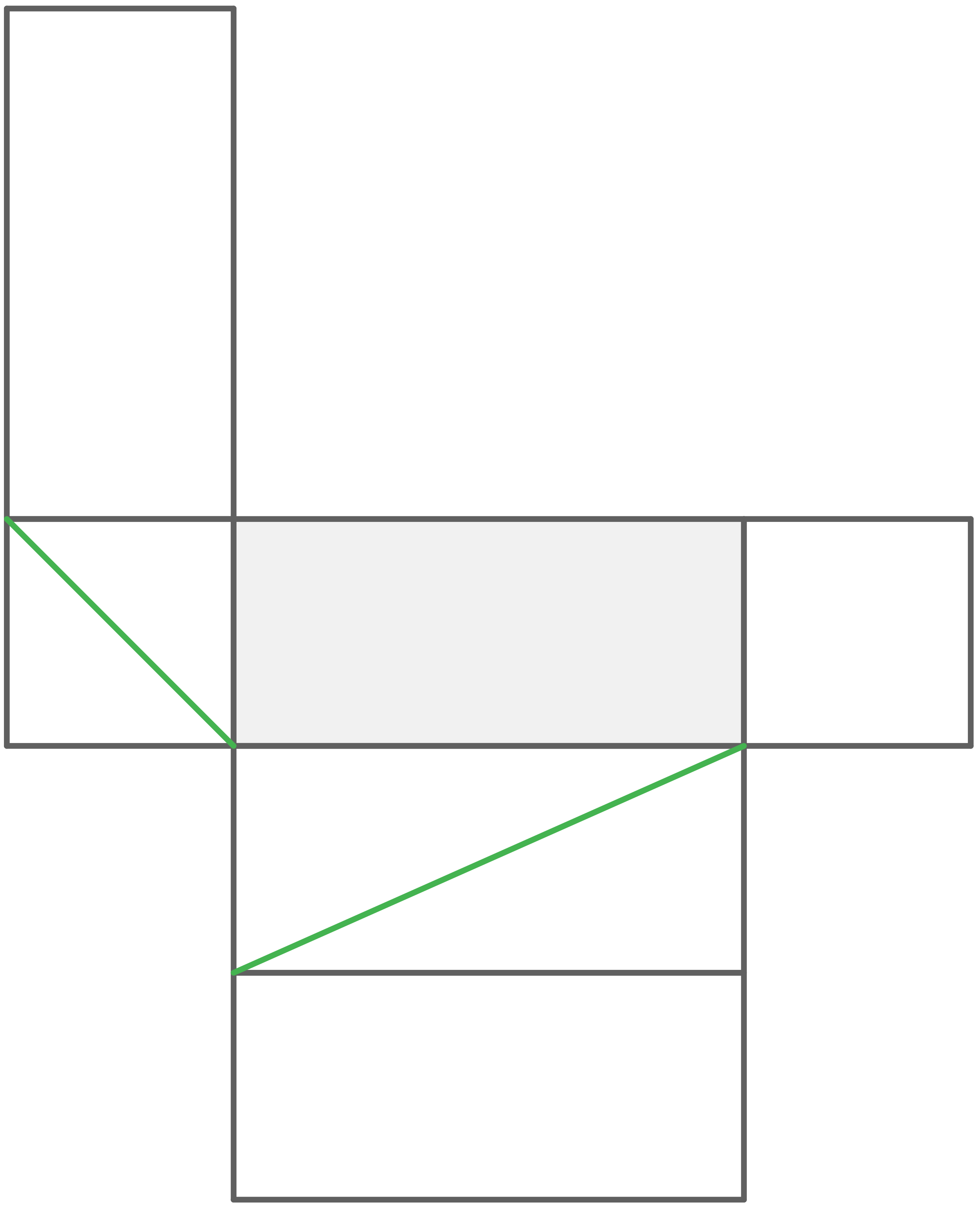
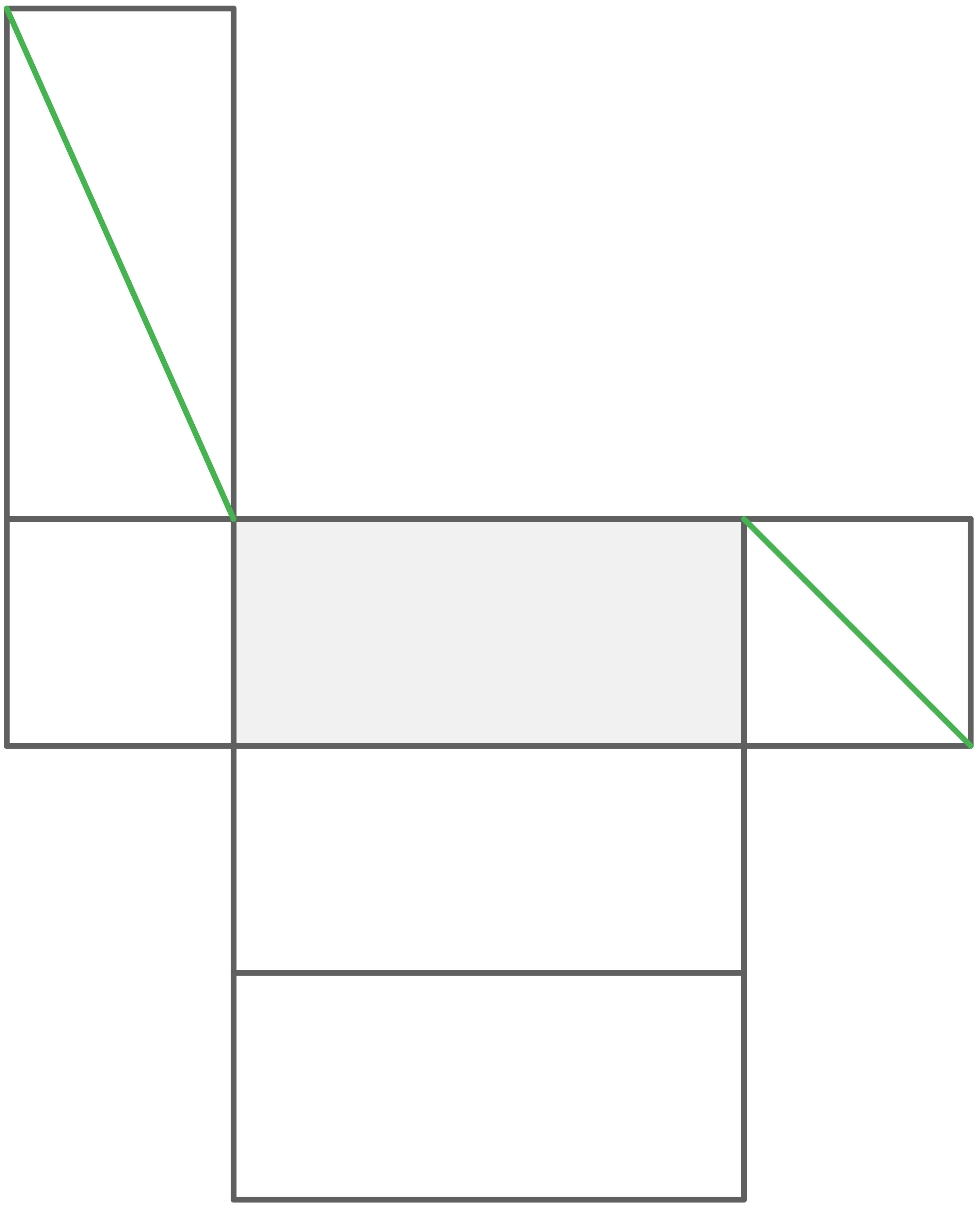


7.
Der Flächeninhalt eines Parallelogramms wird berechnet über  Um zu begründen, ob alle Parallelogramme denselben Flächeninhalt haben, reicht es also sich die Höhe und die Grundseite anzuschauen.
Um zu begründen, ob alle Parallelogramme denselben Flächeninhalt haben, reicht es also sich die Höhe und die Grundseite anzuschauen.
- Jedes der drei Parallelogramme hat die gleiche Höhe.
- Durch Abmessen sieht man, dass auch die Grundseiten der drei Parallelogramme gleich lang sind.
8.
1. Schritt: Alle Noten addieren
 2. Schritt: Anzahl der Schüler*innen der 9b bestimmen
Durch Zählen der Striche, ergibt sich eine Schüler*innen-Anzahl von 17.
3. Schritt: Notendurchschnitt berechnen
2. Schritt: Anzahl der Schüler*innen der 9b bestimmen
Durch Zählen der Striche, ergibt sich eine Schüler*innen-Anzahl von 17.
3. Schritt: Notendurchschnitt berechnen
 Der Notendurchschnitt beträgt also
Der Notendurchschnitt beträgt also 
9.
- Prozentuale Verteilung der roten Gummibärchen:
- Prozentuale Verteilung der grünen Gummibärchen:
- Prozentuale Verteilung der gelben Gummibärchen:
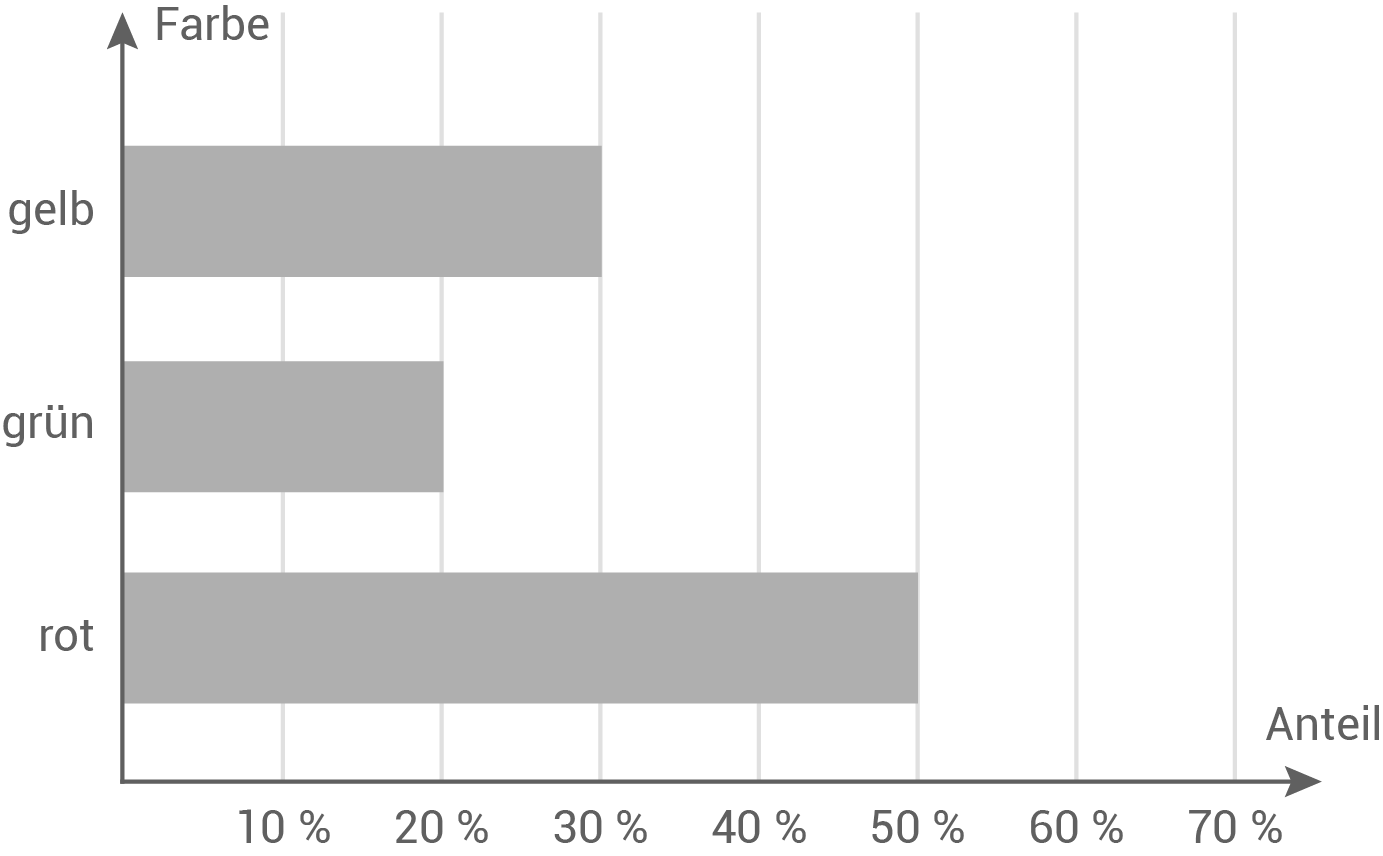
10.
Um von 120 Schrauben auf 240 Schrauben zu kommen, muss mit 2 multipliziert werden.
 Mit dieser Info kann nun das Gewicht der 240 Schrauben eingetragen werden:
Mit dieser Info kann nun das Gewicht der 240 Schrauben eingetragen werden:
Mit dem Dreisatz kann die Anzahl der Schrauben bei  Gewicht berechnet werden:
Gewicht berechnet werden:




![\(\begin{array}{rcl}
120\,\text{Schrauben} & \mathrel{\widehat{=}}& 30\,\text{g}\\[5pt]
40\,\text{Schrauben} & \mathrel{\widehat{=}}& 10\,\text{g}\\[5pt]
80\,\text{Schrauben} & \mathrel{\widehat{=}}& 20\,\text{g}
\end{array}\)](https://www.schullv.de/resources/formulas/5a96dd152f486fa8dede49f6bd1020660dcfadc2de65546d26c252b89e9a9f67_light.svg)





| Gewicht in g | 20 | 30 | 60 |
|---|---|---|---|
| Anzahl der Schrauben | 120 | 240 |
| Gewicht in g | 20 | 30 | 60 |
|---|---|---|---|
| Anzahl der Schrauben | 80 | 120 | 240 |