Grundkenntnisse
1.
Kreuze die Aufgabe an, die das größte Ergebnis hat.
(1 Pkt.)
2.
Can bezahlt folgenden Einkauf mit  :
:
- zwei Paar Socken für je
- ein Hemd für
- ein Paar Schuhe für
(1 Pkt.)
3.
Welche Angabe passt? Kreuze an:
a)
Größe einer Person:
b)
Alter eines 15-jährigen Schülers:
(1 Pkt.)
4.
Welche Zahlen sind am Zahlenstrahl dargestellt?
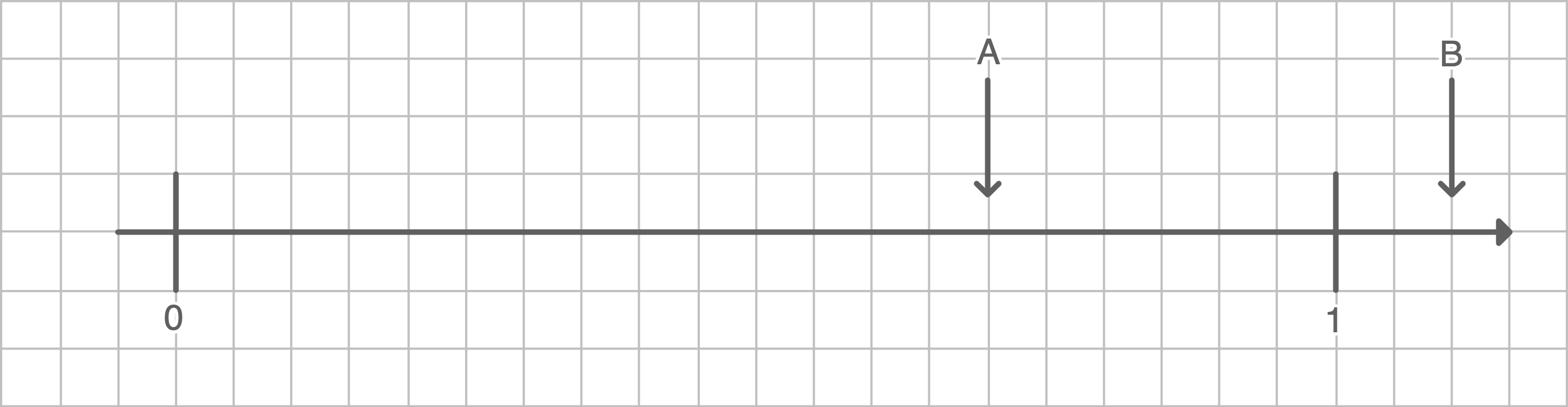



(1 Pkt.)
5.
Miss die Winkel in diesem Viereck.
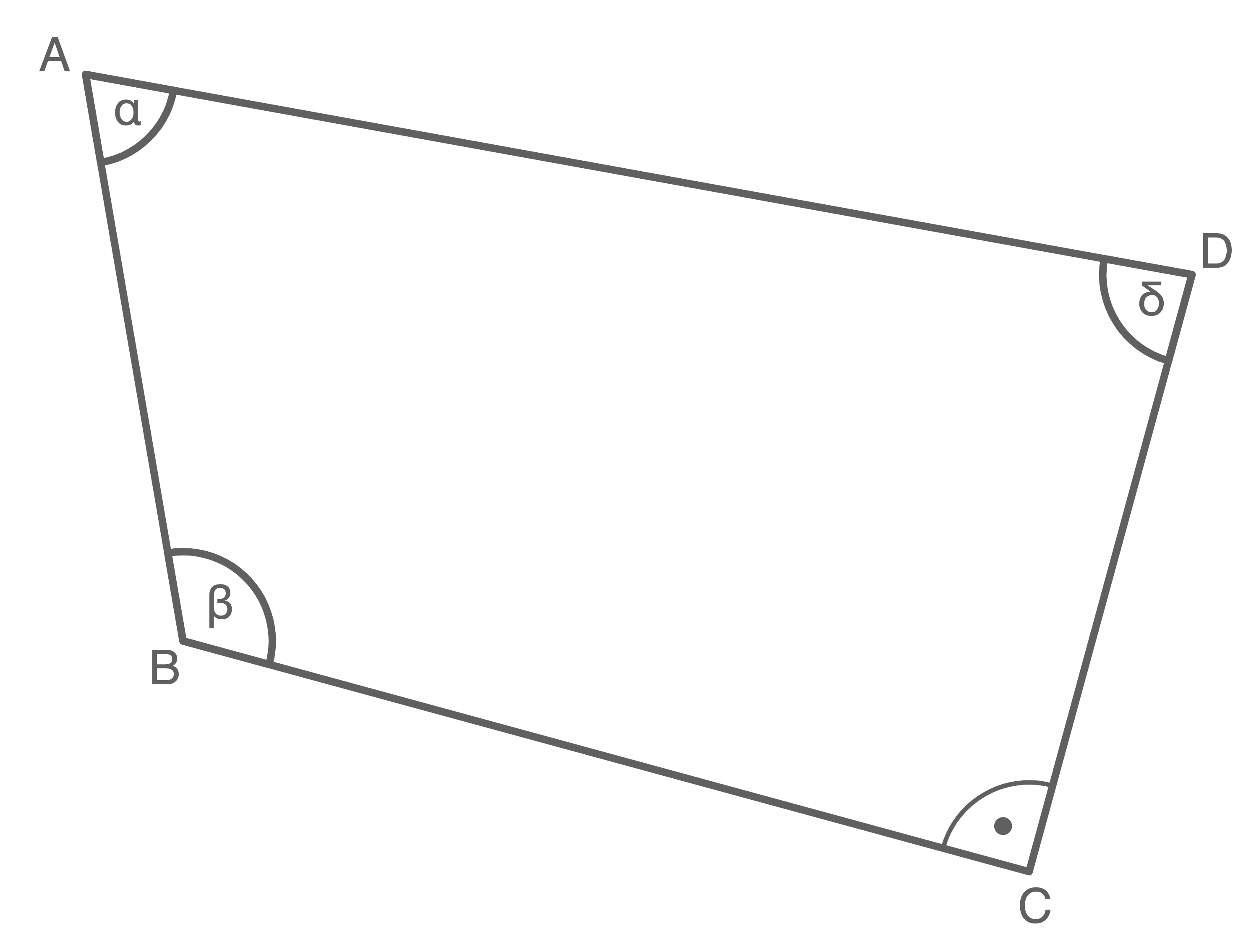





(1 Pkt.)
6.
Wie groß ist die Wahrscheinlichkeit, einen Kleingewinn zu erhalten, wenn man einmal am Glücksrad dreht?
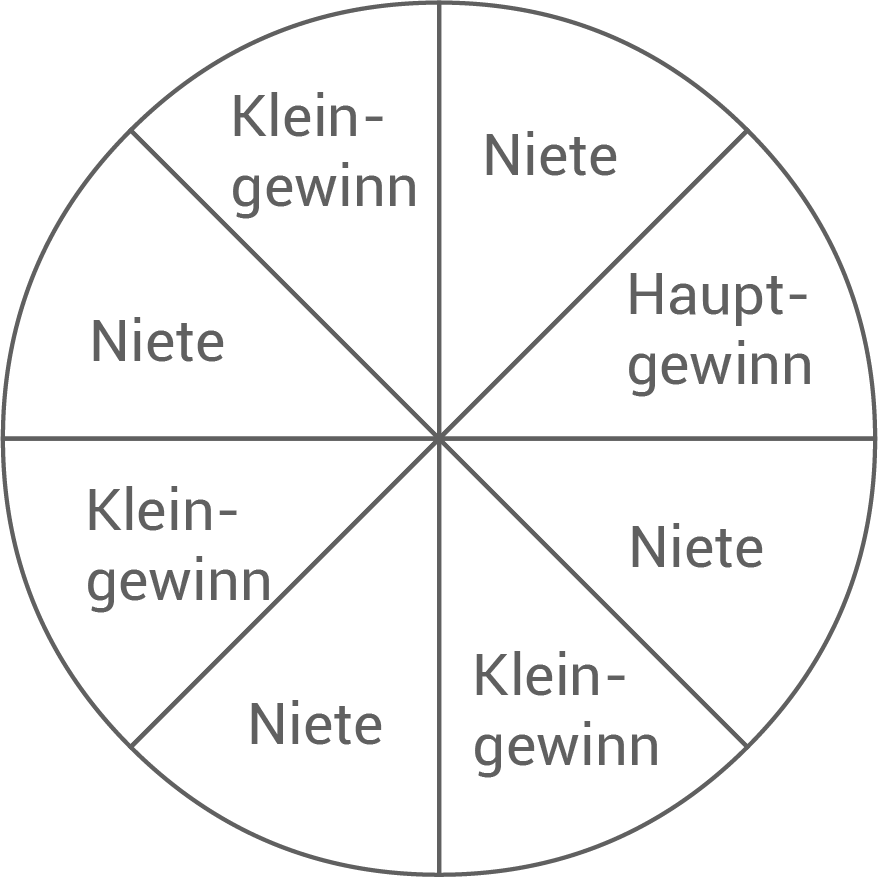

(1 Pkt.)
7.
Löse die Gleichung.

(1 Pkt.)
8.
Wie viele Zinsen werden nach einem Jahr ausbezahlt?
Spareinlage
- Kapital:
- Zinssatz:
(1 Pkt.)
9.
Ermittle die Oberfläche des Körpers.
Die Kantenlänge eines Würfels beträgt
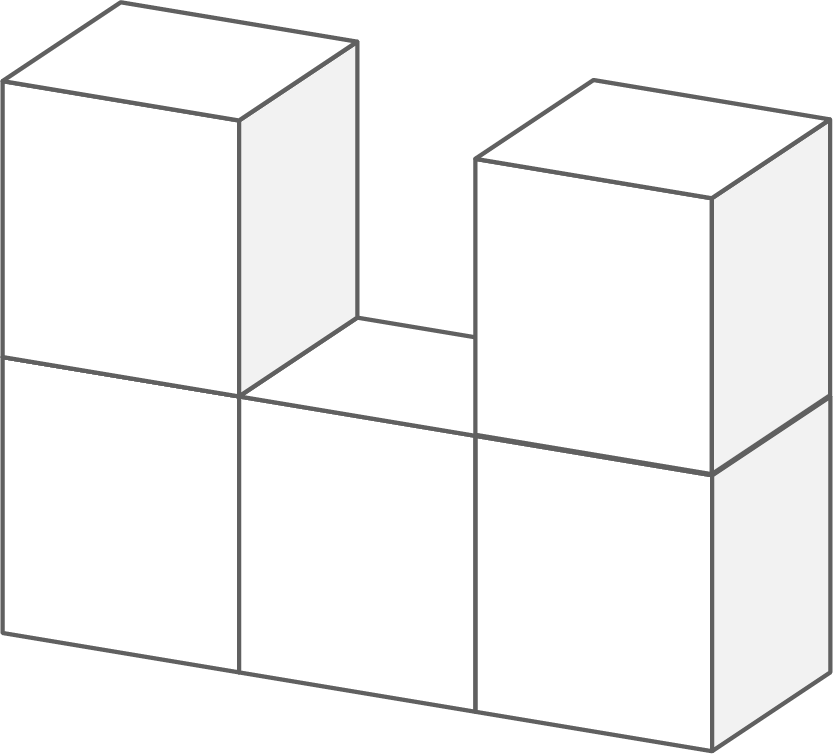
Die Kantenlänge eines Würfels beträgt

(1 Pkt.)
10.
Das Diagramm zeigt die erzielten Punkte bei einem Wurfspiel.
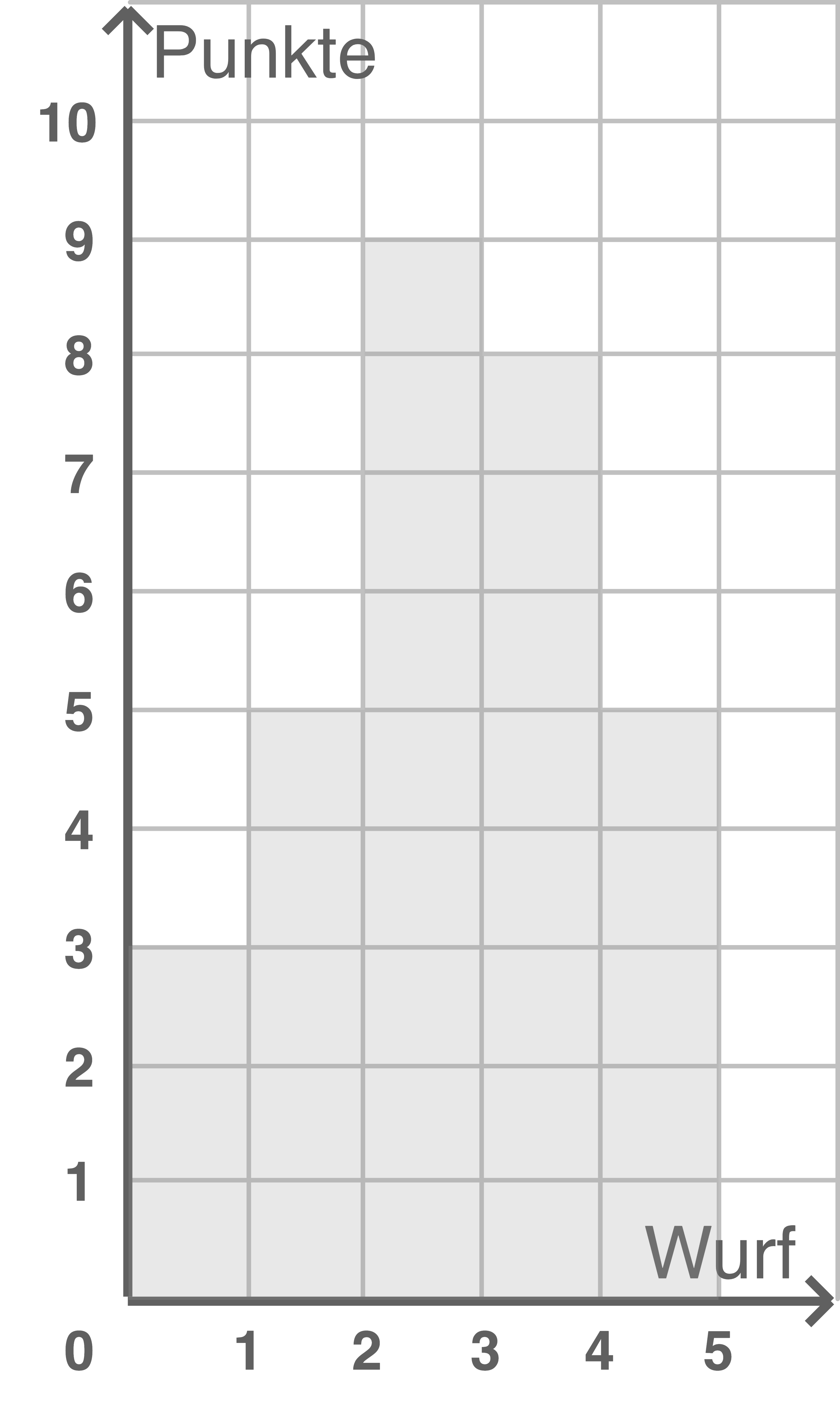 Berechne die durchschnittliche Punktzahl nach 5 Würfen.
Berechne die durchschnittliche Punktzahl nach 5 Würfen.

(1 Pkt.)
1.
2.
Gesamtkosten für den Einkauf berechnen
Rückgeld berechnen
Can bekommt  zurück.
zurück.
| , | ||||||||||
| , | ||||||||||
| , | ||||||||||
| , | ||||||||||
| , |
| , | ||||||||||
| , | ||||||||||
| , |
3.
a)
Größe einer Person:
Umrechnungen
b)
Alter eines 15-jährigen Schülers:
Umrechnungen
4.
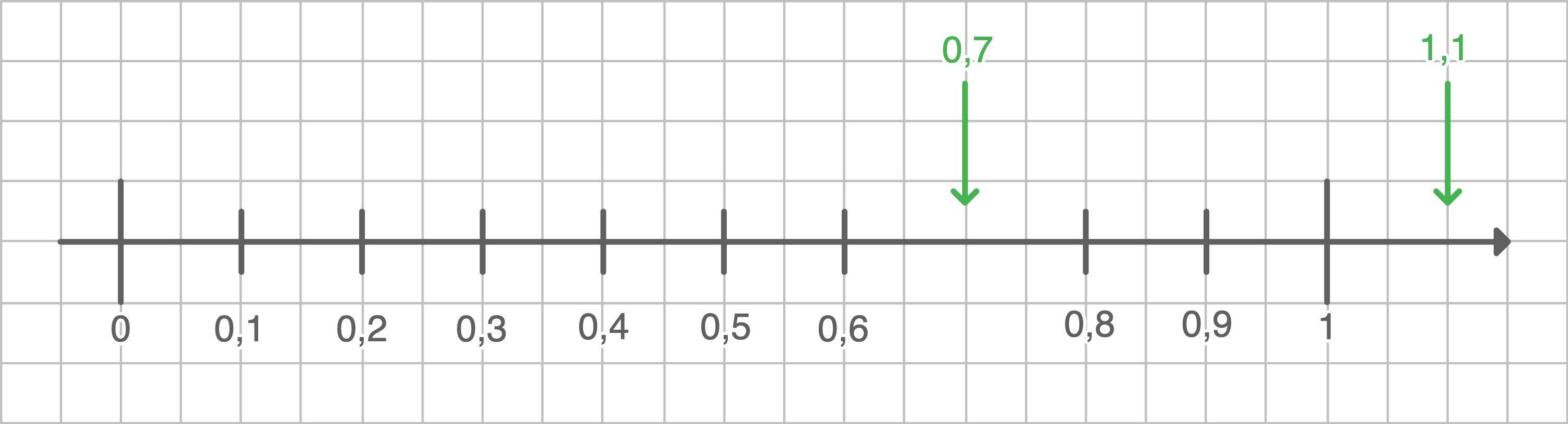
5.
6.
Das Glücksrad hat insgesamt 8 Felder. Davon sind 3 Felder mit „Kleingewinn“ beschriftet.
Damit lässt sich die Wahrscheinlichkeit aufstellen: 
7.
8.
Lösung über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}&5\,000\,€\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 50\,€\\[5pt]
0,5\,\% & \mathrel{\widehat{=}}& 25\,€
\end{array}\)](https://www.schullv.de/resources/formulas/c96cd58b809697bf66f85da40bc49f7e7e8bc14355707fa692a376e2b31acf68_light.svg)




Lösung über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} \\[5pt]
P&=&\dfrac{5\,000\,€\cdot 0,5}{100} \\[5pt]
P&=&25\,€ \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fdca061d536d51910a7471c375e14adf8bec479c4906304683e0be8cbaaad7af_light.svg)
Nach einem Jahr werden
9.
Der Körper besteht aus 5 Würfeln. Jeder Würfel hat 6 Seiten.
5 Würfel haben also insgesamt  Seiten.
Bei diesem Körper gehören 8 Seite nicht zur Oberfläche.
Seiten.
Bei diesem Körper gehören 8 Seite nicht zur Oberfläche.
Der Körper besteht also aus Seiten.
Oberflächeninhalt einer Seite berechnen
Seiten.
Oberflächeninhalt einer Seite berechnen
![\(\begin{array}[t]{rll}
O_1&=&a^2 \\[5pt]
O_1&=&(2\,\text{cm})^2 \\[5pt]
O_1&=&4\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5762be0dce255ab031b449b8b99b48182fbad86767c161732c91577456a4ceeb_light.svg) Gesamten Oberflächeninhalt berechnen
Gesamten Oberflächeninhalt berechnen
![\(\begin{array}[t]{rll}
O_\text{gesamt}&=&22\cdot O_1 \\[5pt]
O_\text{gesamt}&=&22\cdot 4\,\text{cm}^2 \\[5pt]
O_\text{gesamt}&=&88\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/51829782149efe953114969c57cc009eafb8aaa444a72d791d5587967d197c59_light.svg)
Der Körper besteht also aus
10.