Wahlpflichtaufgaben

Aufgabe 1 – Spielzeug

In der unten stehenden Tabelle kannst du ablesen, für welche Anlässe Spielzeug gekauft wird.

Kaufanlass	Angaben in %
Geburtstag	$24$
Weihnachten	$23$
Ostern	$4$
Belohnung	$6$
Sonstige	$43$

Zeichne ein passendes Streifendiagramm.

(2 Pkt.)

Benjamin kauft einen Bausatz für $59,90 \,€$ und ein Brettspiel für $39,95 \,€.$
Er hat zwei verschiedene Gutscheine.

Welchen Gutschein sollte er für den Bausatz einsetzen, um möglichst wenig bezahlen zu müssen? Begründe deine Entscheidung.
Wie viel Euro muss er insgesamt bezahlen, wenn er auch noch den anderen Gutschein für das Brettspiel einsetzt?

(2 Pkt.)

Um das abgebildete Spielbrett in einer rechteckigen Schachtel zu verpacken, wird es an der gestrichelten Linie zusammengeklappt. Dadurch wird die Höhe des Spielbretts halbiert.

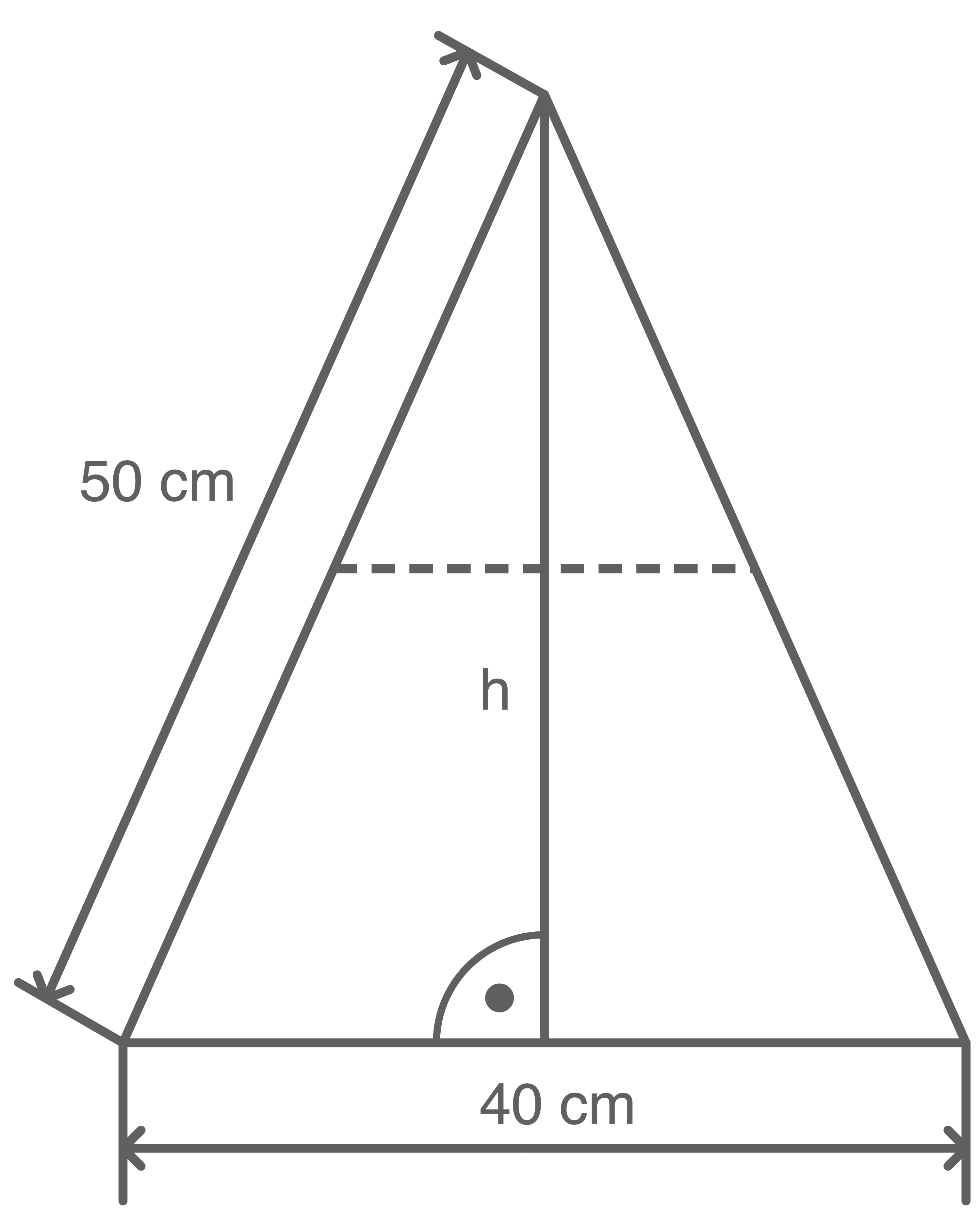Berechne die Länge und Breite der Schachtel, wenn das Spielbrett zum Schachtelrand genau $1 \,\text{cm}$ Platz haben soll.

(2 Pkt.)

Aufgabe 2 – Pizza

In Tonis Pizzeria kann man seine Pizza selbst zusammenstellen.

Fleisch	Gemüse	Käse
Schinken	Champignons	Mozzarella
Salami	Paprika	Parmesan
Hackfleisch	Tomaten

Wie viele verschiedene Möglichkeiten gibt es, wenn man aus den Bereichen Fleisch, Gemüse und Käse jeweils genau eine Zutat nimmt?

(2 Pkt.)

Toni legt nach und nach eine Pizza, im Karton verpackt, in die Transportbox.

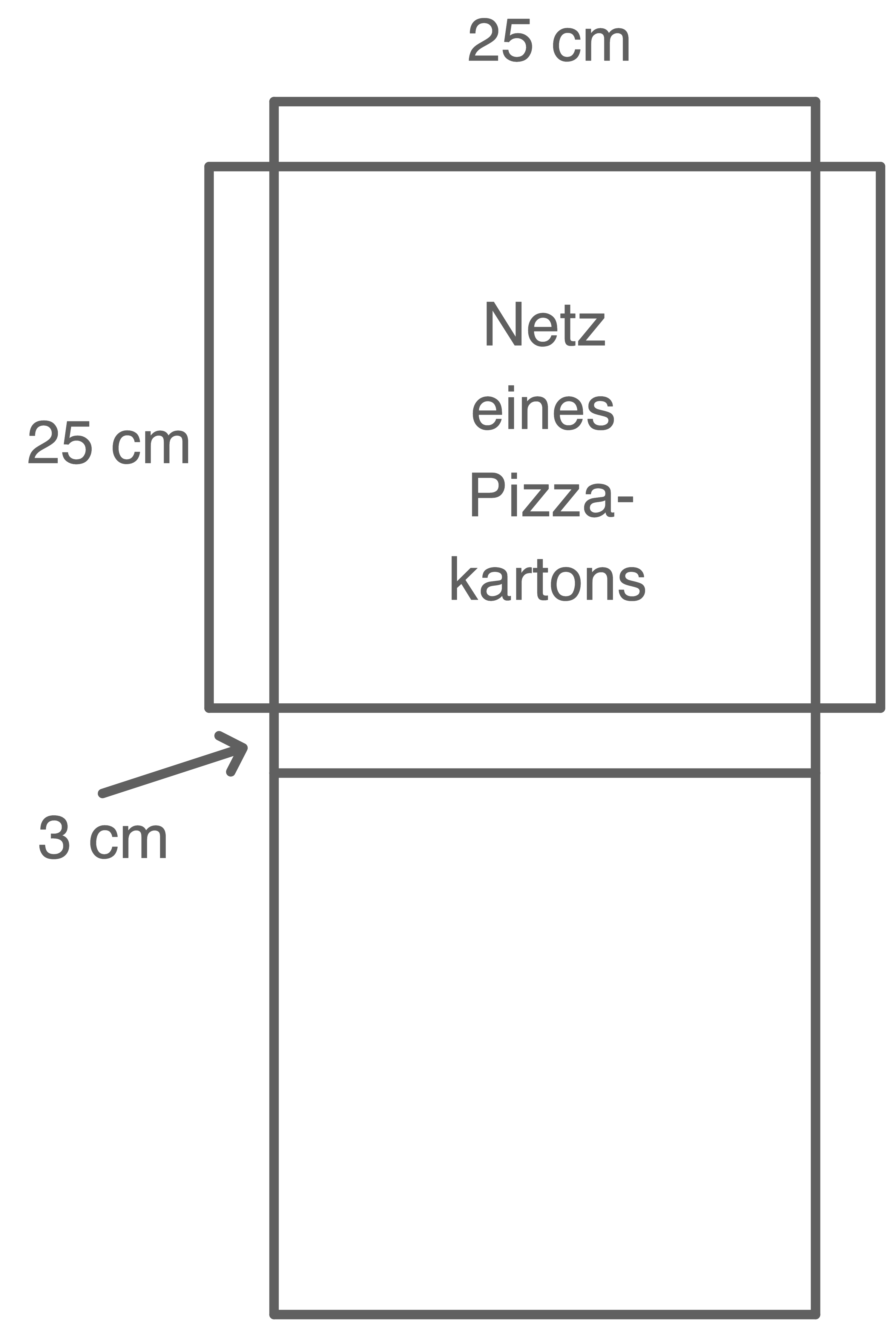
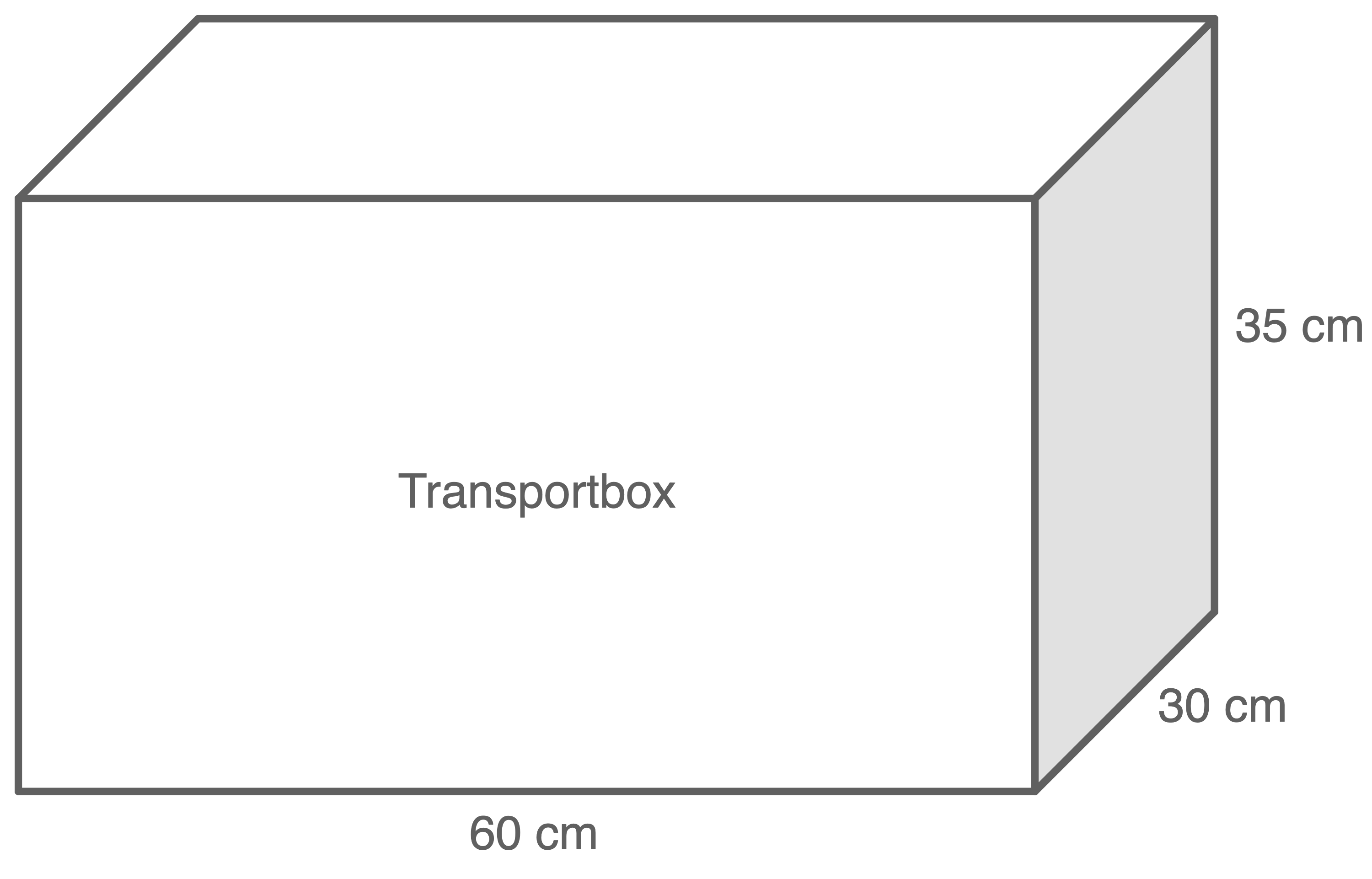Wie viele Kartons kann Toni höchstens in seiner Transportbox unterbringen?

(2 Pkt.)

Bei welcher Pizzagröße bekommst du für $36 \,€$ insgesamt die größte Pizzafläche?

Pizzagröße	Margherita
Klein ∅ $\color{#ffffff}{24\,\text{cm}}$	$3,00 \,€$
Groß ∅ $\color{#ffffff}{32\,\text{cm}}$	$6,00 \,€$
Party $\color{#ffffff}{60}$ x $\color{#ffffff}{40\,\text{cm}}$	$18,00 \,€$

Gib die Größe der Fläche an.

(2 Pkt.)

Aufgabe 3 – USA

Sarah fliegt in die USA und möchte wissen, zu welcher Ortszeit sie in San Francisco ankommt.

Hinflug Ortszeit Frankfurt	Montag, 27. Juni, 13:55 Uhr
Flugdauer	11 h 15 min
Ankunft Ortszeit San Francisco	?

(2 Pkt.)

Welche Fläche hat der Bundesstaat Nevada ungefähr?

$1\,\text{cm}$ entspricht $88\,\text{km}.$

hauptschulabschluss mathe 2017 baden-württemberg

(2 Pkt.)

Die USA hatten im Jahre 2015 eine Verschuldung von 18 Billionen Dollar.

USA im Jahr 2015

Einwohnerzahl: $319$ Mio.
Verschuldung: $18$ Bio. Dollar

Schreibe die Verschuldung als Zehnerpotenz.
Berechne die durchschnittliche Verschuldung pro Einwohner.

(2 Pkt.)

Aufgabe 4 – Waschen

Das Diagramm zeigt die prozentuale Entwicklung der verwendeten Waschtemperaturen.

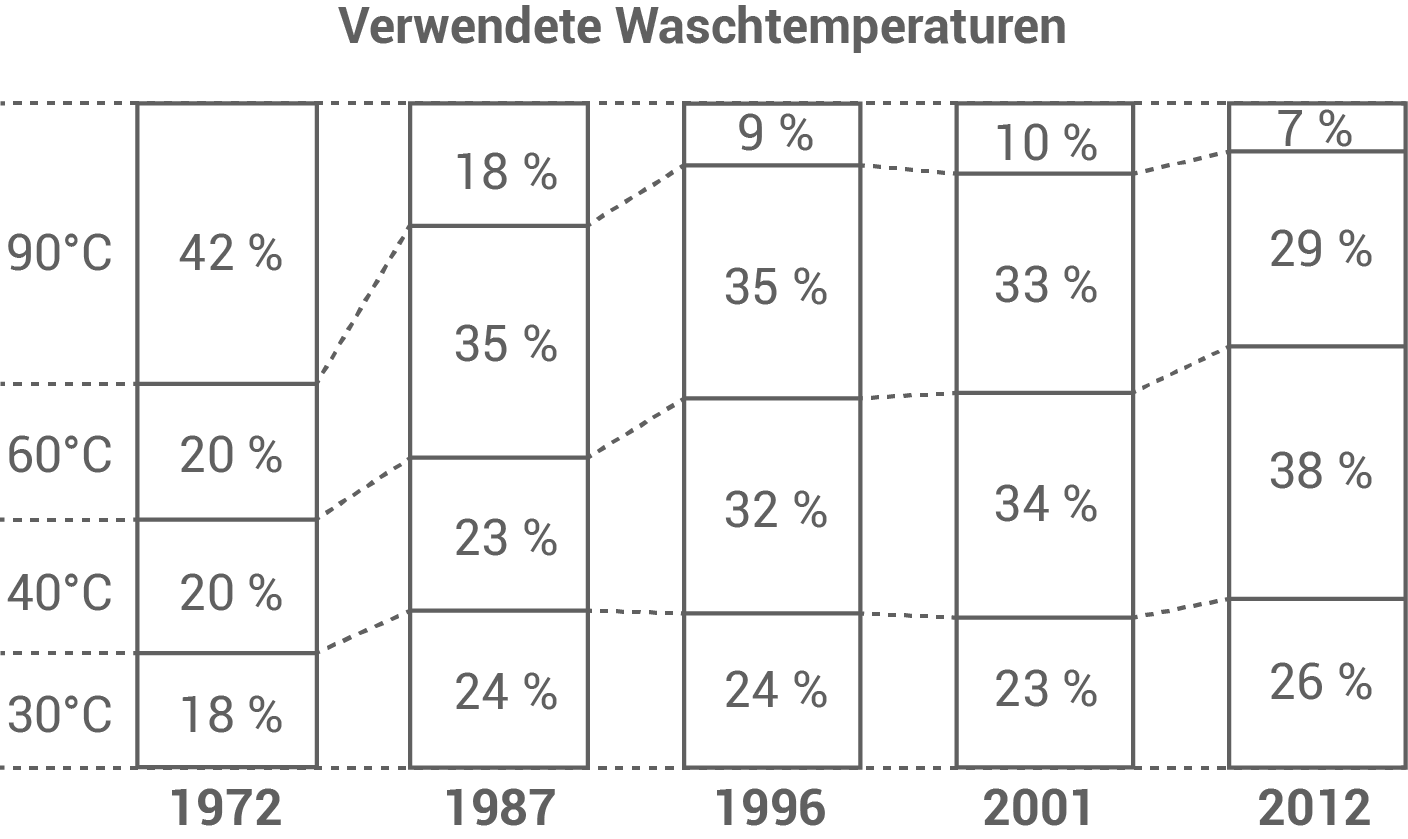
Bei welcher Waschtemperatur ist der Wert von 1972 bis 2012 um $35$ Prozentpunkte gesunken?
Die Verwendung welcher Waschtemperatur ist in dem abgebildeten Diagramm prozentual ständig angestiegen?

(2 Pkt.)

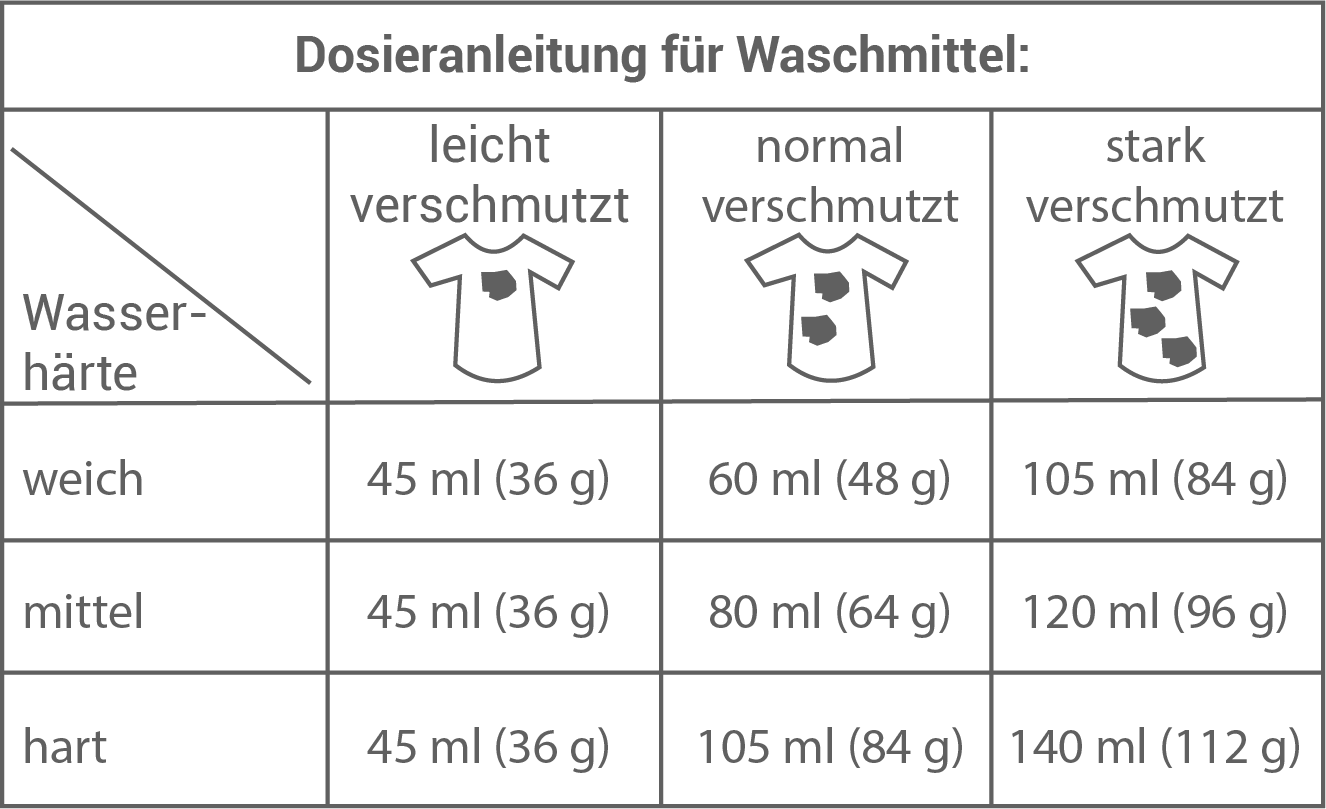
Waschmittel wird meistens überdosiert. Deswegen ändert Familie Mayer ihre Dosierung.
Ihre alte Dosierung:
„Normal verschmutzt" bei Wasserhärte „hart“.
Ihre neue Dosierung:
„Leicht verschmutzt" bei Wasserhärte „mittel“.

HSA 2017 BAWÜ Waschen Temperatur Dosierung

Wie viel Liter Waschmittel spart sie bei 220 Waschvorgängen ein?

(2 Pkt.)

Eine Waschmaschinentrommel (siehe Abbildung) hat einen Durchmesser von $49 \,\text{cm}$ .

HSA 2017 BAWÜ Waschmaschinentrommel kreis

Wenn die Wäsche geschleudert wird, dreht sich der äußerste Punkt der Trommel mit $1\,600$ Umdrehungen pro Minute.
Peter stellt sich vor, dass die Waschmaschinentrommel das Rad eines Fahrzeugs wäre.
Mit welcher Geschwindigkeit wäre das Fahrzeug unterwegs?

(2 Pkt.)

Lösung 1

Am einfachsten ist es, einen $10\,\text{cm}$ langen Streifen zu wählen, denn $10\,\text{cm}=100\,\text{mm}.$
Somit gilt: $1\,\text{mm}$ entspricht $1\,\%.$

Kaufanlass	Angaben in %	Länge des Segments
Geburtstag	$24$	$24\,\text{mm}$
Weihnachten	$23$	$23\,\text{mm}$
Ostern	$4$	$4\,\text{mm}$
Belohnung	$6$	$6\,\text{mm}$
Sonstige	$43$	$43\,\text{mm}$

Welchen Gutschein sollte er für den Bausatz einsetzen?

Beim Einlösen des 10 € Rabatts spart Benjamin $10\,€.$ Um die Gutscheine vergleichen zu können, muss berechnet werden, wie viel Euro Benjamin beim Einlösen des 20 % Rabatts spart:

Lösung über den Dreisatz

$:100$

$\cdot 20$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 100\,\% & \mathrel{\widehat{=}}& 59,90\,€\\[5pt] 1\,\% & \mathrel{\widehat{=}}& 0,599\,€\\[5pt] 20\,\% & \mathrel{\widehat{=}}& 11,98\,€ \end{array}$

$:100$

$\cdot 20$

Lösung über die Formel

$\begin{array}[t]{rll} P&=&\dfrac{G\cdot p}{100} \\[5pt] P&=&\dfrac{59,90\,€\cdot 20}{100} \\[5pt] P&=&11,98\,€ \\[5pt] \end{array}$

Benjamin sollte den Gutschein „20 % Rabatt“ einlösen, da er hier $11,98\,€$ spart.

Wie viel Euro muss er insgesamt bezahlen, wenn er den anderen Gutschein für das Brettspiel einsetzt?

Kosten für den Bausatz: $59,90 \,€-11,98=47,92\,€$

Kosten für das Brettspiel: $39,95 \,€-10,00\,€=29,95\,€$

Gesamtkosten: $47,92\,€+29,95\,€=77,87\,€$

Benjamin muss insgesamt $77,87\,€$ bezahlen.

Höhe des Spielbretts berechnen

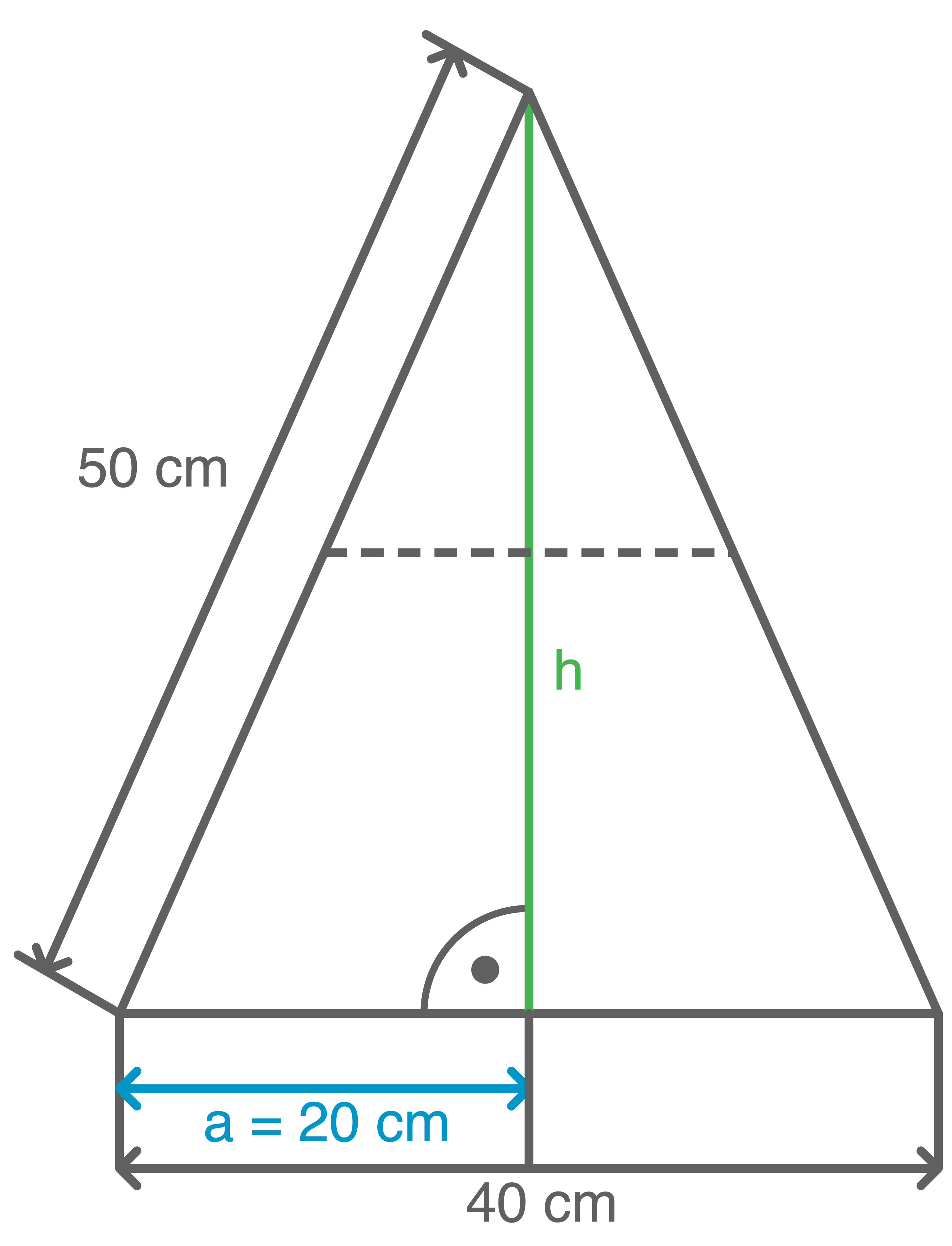Satz des Pythagoras anwenden:

$\begin{array}[t]{rll} h^2+a^2&=&(50\,\text{cm})^2 &\quad \scriptsize \mid\;-a^2 \\[5pt] h^2&=&(50\,\text{cm})^2-a^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt] h&=&\sqrt{(50\,\text{cm})^2-a^2} &\\[5pt] h&=&\sqrt{(50\,\text{cm})^2-(20\,\text{cm})^2} \\[5pt] h&\approx &45,8\,\text{cm} \\[5pt] \end{array}$

Breite der Schachtel berechnen

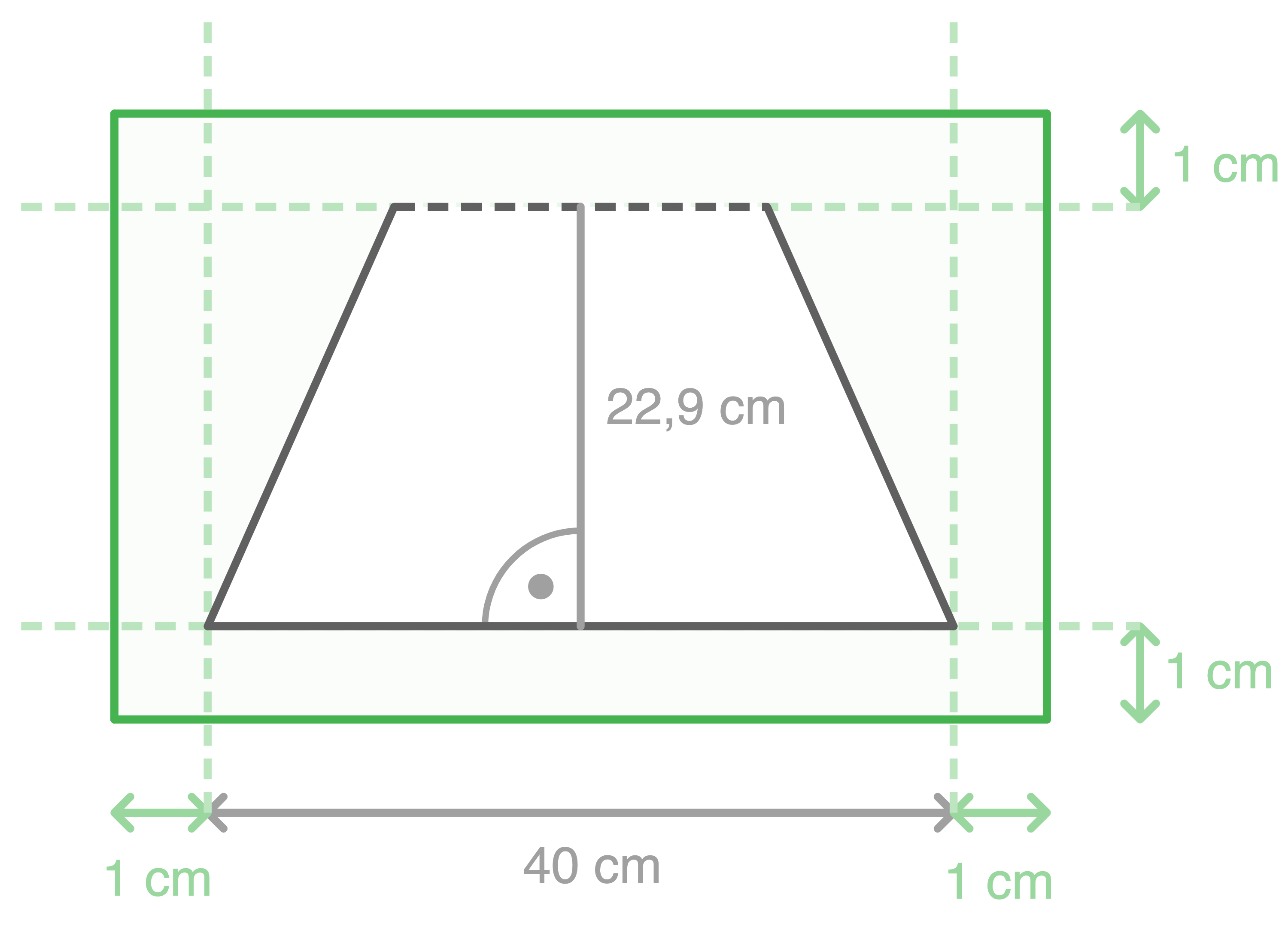Da das Spielbrett an der gestrichelten Linie zusammengeklappt wird, muss die Höhe durch zwei geteilt werden: $45,8\,\text{cm}:2=22,9\,\text{cm}$

Daraus ergibt sich für die Breite der Schachtel: $22,9\,\text{cm}+1\,\text{cm}+1\,\text{cm}=24,9\,\text{cm}$

Länge der Schachtel berechnen

$40\,\text{cm}+1\,\text{cm}+1\,\text{cm}=42\,\text{cm}$

Lösung 2

Um den Überblick über alle Möglichkeiten zu bewahren, hilft es ein Baumdiagramm zu erstellen:

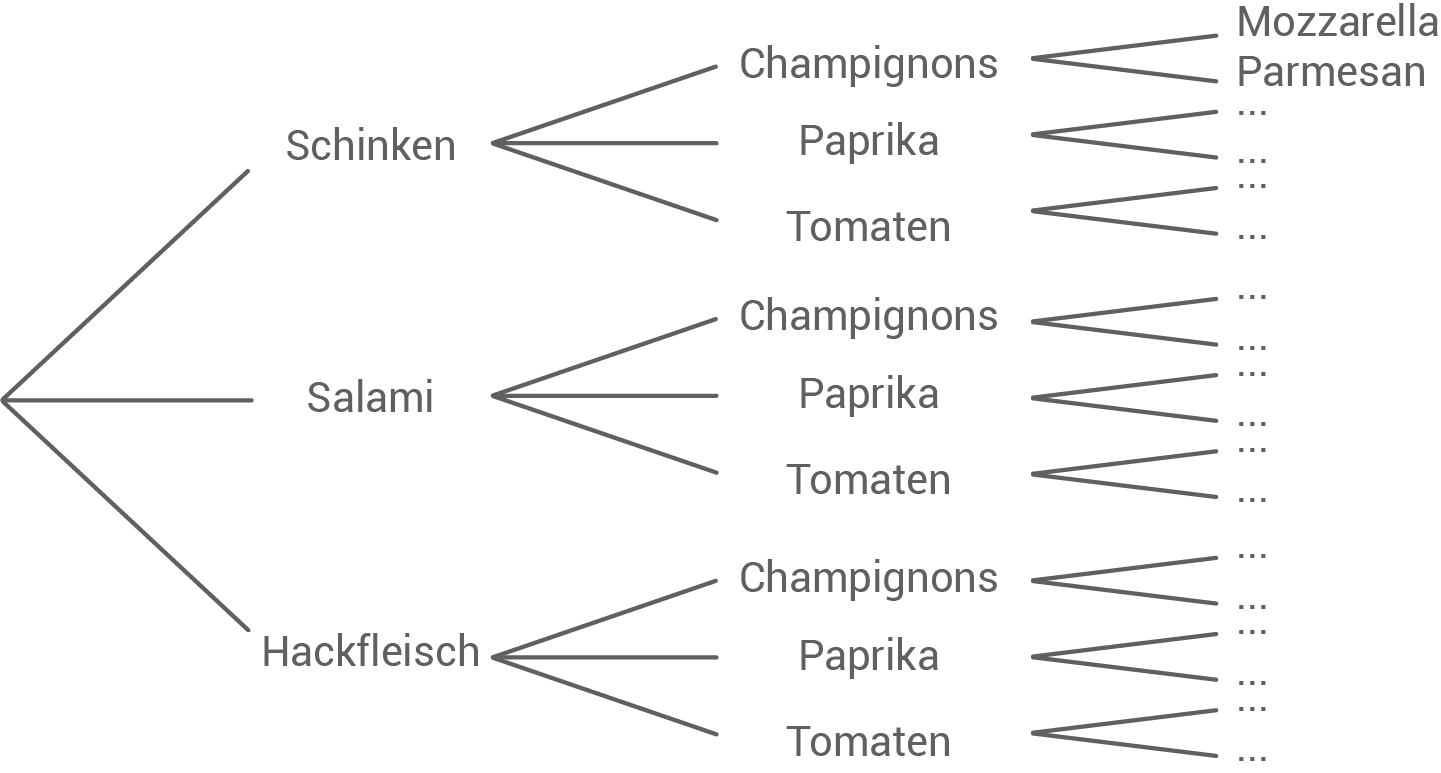Um die Anzahl aller Möglichkeiten zu ermitteln, müssen die Pfade im letzten Schritten gezählt werden: Es gibt also 18 Möglichkeiten.

Maße eines Pizzakartons

$25\,\text{cm}$ breit
$3\,\text{cm}$ hoch

Maße der Transportbox

$60\,\text{cm}$ breit
$35\,\text{cm}$ hoch

Daraus folgt

Nebeneinander passen $2$ Pizzakartons.
Übereinander passen $11$ Pizzakartons.
Insgesamt passen $2\cdot 11=22$ Pizzakartons in die Transportbox.

Kleine Pizza

Anzahl
$36\,€:3\,€=12$
Für $36\,€$ können $12$ kleine Pizzas gekauft werden.
Flächeninhalt
$r=d:2=24\,\text{cm}:2=12\,\text{cm}$
$\begin{array}[t]{rll} A_1&=& 12\cdot \pi\cdot r^2\\[5pt] A_1&=& 12\cdot \pi\cdot (12\,\text{cm})^2\\[5pt] A_1&\approx&5\,428,7\,\text{cm}^2 \end{array}$

Große Pizza

Anzahl
$36\,€:6\,€=6$
Für $36\,€$ können $6$ große Pizzas gekauft werden.
Flächeninhalt
$r=d:2=32\,\text{cm}:2=16\,\text{cm}$
$\begin{array}[t]{rll} A_2&=& 6\cdot \pi\cdot r^2\\[5pt] A_2&=& 6\cdot \pi\cdot (16\,\text{cm})^2\\[5pt] A_2&\approx&4\,825,5\,\text{cm}^2 \end{array}$

Party-Pizza

Anzahl
$36\,€:18\,€=2$
Für $36\,€$ können $2$ Party-Pizzas gekauft werden.
Flächeninhalt
Die Party-Pizza hat eine rechteckige Form:
$\begin{array}[t]{rll} A_3&=& 2\cdot a\cdot b\\[5pt] A_3&=& 2\cdot 60\,\text{cm}\cdot 40\,\text{cm}\\[5pt] A_3&=& 4\,800\,\text{cm}^2 \end{array}$

Bei der kleinen Pizza bekommt man für $36\,€$ die größte Fläche $A_1=5\,428,7\,\text{cm}^2.$

Lösung 3

Ankunft ohne Zeitverschiebung

$13:55\,\text{Uhr}+11\,\text{h}= 24:55\,\text{Uhr}=0:55\,\text{Uhr}$

$0:55\,\text{Uhr}+15\,\text{min}= 1:10\,\text{Uhr}$

Ankunft mit Zeitverschiebung

$1:10\,\text{Uhr}-9\,\text{h}= 16:10\,\text{Uhr}$

Sarah kommt um $16:10\,\text{Uhr}$ Ortszeit in San Francisco an.

Um den Flächeninhalt zu berechnen, wird die Fläche in berechenbare Teilflächen zerlegt und jeweils die Länge und Breite der Rechtecke abgemessen.

Eine mögliche Zerlegung:

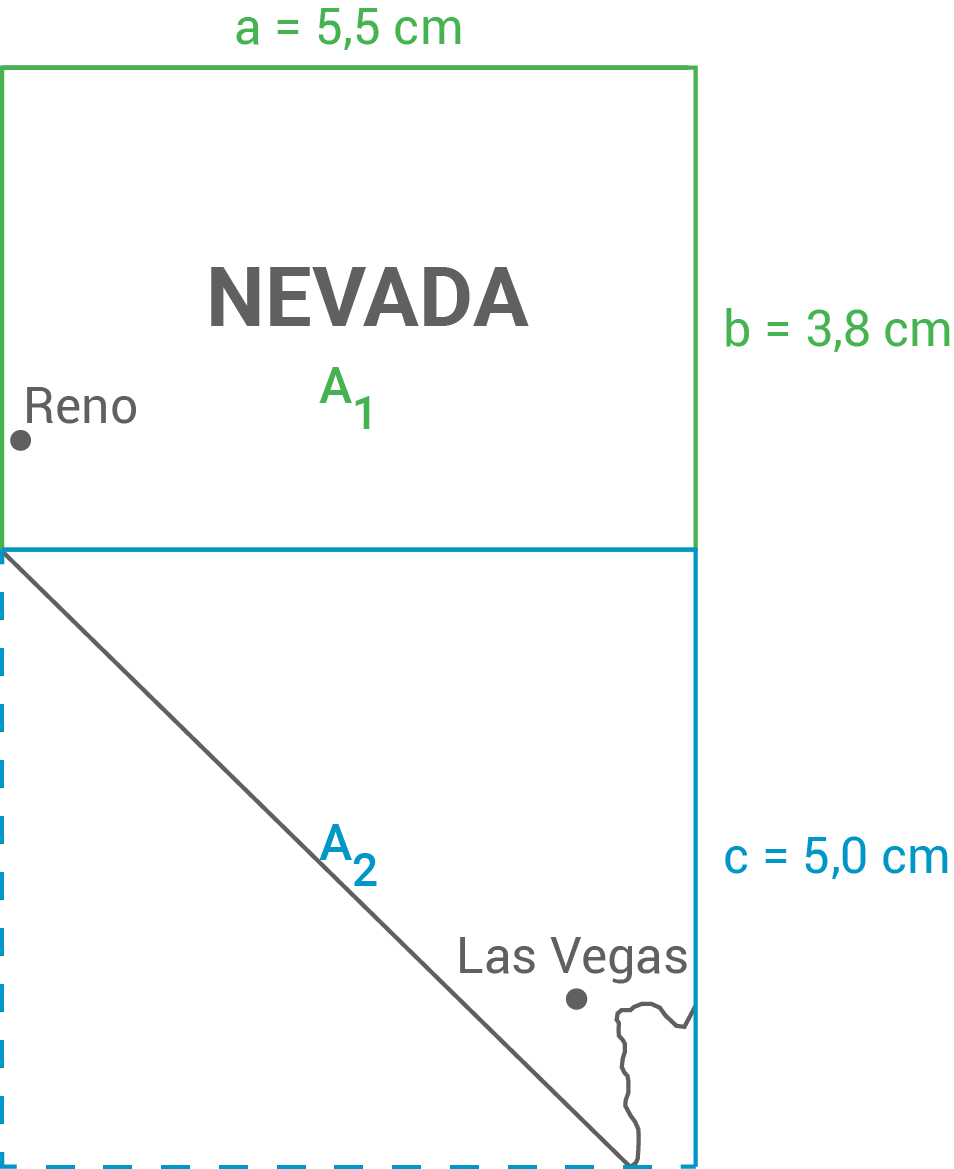Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

Bevor der Flächeninhalt berechnet werden kann, müssen die abgemessenen Längen in die wirklichen Längen umgerechnet werden:

$a=5,5\cdot 88\,\text{km}=484\,\text{km}$
$b=3,8\cdot 88\,\text{km}=334,4\,\text{km}$
$c=5,0\cdot 88\,\text{km}=440\,\text{km}$

Flächeninhalt von $\boldsymbol{A_1}$ berechnen

$\begin{array}[t]{rll} A_1&=&a\cdot b \\[5pt] A_1&=&484\,\text{km}\cdot 334,4\,\text{km} \\[5pt] A_1&=&161\,849,6\,\text{km}^2 \end{array}$

Flächeninhalt von $\boldsymbol{A_2}$ berechnen

Die zweite Fläche lässt sich annährend als Dreieck beschreiben:
$\begin{array}[t]{rll} A_2&=&\dfrac{a\cdot c}{2} \\[5pt] A_2&=&\dfrac{484\,\text{km}\cdot 440\,\text{km}}{2} \\[5pt] A_2&=&106\,480\,\text{km}^2 \\[5pt] \end{array}$

Gesamten Flächeninhalt berechnen

$\begin{array}[t]{rll} A_{\text{gesamt}}&=&A_1+A_2 \\[5pt] A_{\text{gesamt}}&=&161\,849,6\,\text{km}^2+106\,480\,\text{km}^2 \\[5pt] A_{\text{gesamt}}&=&268\,329,6\,\text{km}^2 \\[5pt] \end{array}$

Verschuldung als Zehnerpotenz schreiben

$1\,\text{Billion}=1\,000\,000\,000\,000=10^{12}$

$18\,\text{Billionen Dollar}=\boldsymbol{18\cdot 10^{12}\,\text{ Dollar}}$ $=\boldsymbol{1,8\cdot 10^{13}\,\text{Dollar}}$

Durchschnittliche Verschuldung pro Einwohner

$1\,\text{Million}=1\,000\,000=10^6$

$319\,\text{Millionen}=319\cdot 10^6$

$18\cdot 10^{12}\,\text{Dollar}:(319\cdot 10^6)\approx 56\,426\,\text{Dollar}$

Die durchschnittliche Verschuldung pro Einwohner betrug etwa $56\,426\,\text{Dollar}.$

Lösung 4

Bei welcher Waschtemperatur ist der Wert von 1972 bis 2012 um 35 Prozentpunkte gesunken?

Bei $90^{\circ}C$ ist der Wert um $35\,\%$ gesunken:

$42\,\%-7\,\%=35\,\%$

Die Verwendung welcher Waschtemperatur ist in dem abgebildeten Diagramm prozentual ständig angestiegen?

$40^{\circ}C$ ist die einzige Waschtemperatur, bei der der Wert prozentual ständig gestiegen ist.

Alte Dosierung: $105\,\text{ml}$
Neue Dosierung: $45\,\text{ml}$

Ersparnis bei einem Waschgang: $105\,\text{ml}-45\,\text{ml}=60\,\text{ml}$

Ersparnis bei 220 Waschvorgängen: $220\cdot 60\,\text{ml}=13\,200\,\text{ml}=13,2\,\text{l}$

Sie spart sich bei 220 Waschvorgängen $13,2$ Liter Waschmittel.

Um die Geschwindigkeit anzugeben, muss berechnet werden, welche Strecke pro Stunde zurückgelegt wird.

Strecke pro Umdrehung berechnen

Diese Strecke entspricht dem Umfang der Trommel.
Dafür wird der Radius benötigt: $r=d:2=49\,\text{cm}:2=24,5\,\text{cm}$

$\begin{array}[t]{rll} u&=&2\cdot \pi\cdot r \\[5pt] u&=&2\cdot \pi\cdot 24,5\,\text{cm} \\[5pt] u&\approx&153,9\,\text{cm} \\[5pt] \end{array}$

Strecke pro Minute berechnen

$1\,600\cdot 153,9\,\text{cm}=246\,240\,\text{cm}\approx 2,46\,\text{km}$

Strecke pro Stunde berechnen

$60\cdot 2,46\,\text{km}=147,60\,\text{km}$

Das Fahrzeug wäre mit $147,60\,\dfrac{\text{km}}{\text{h}}$ unterwegs.