Wahlpflichtaufgaben
Aufgabe 1 – Sport
a)
Gabriel geht 10-mal pro Monat joggen. Seine Trainingsstrecke ist  lang.
lang.
Wie viele Kilometer joggt er in einem Vierteljahr?
Wie viele Kilometer joggt er in einem Vierteljahr?
(2 Pkt.)
b)
Die Skizze zeigt den Verlauf von Onurs Schwimmstrecke.
Wie lang ist seine zurückgelegte Strecke insgesamt?
Wie lang ist seine zurückgelegte Strecke insgesamt?
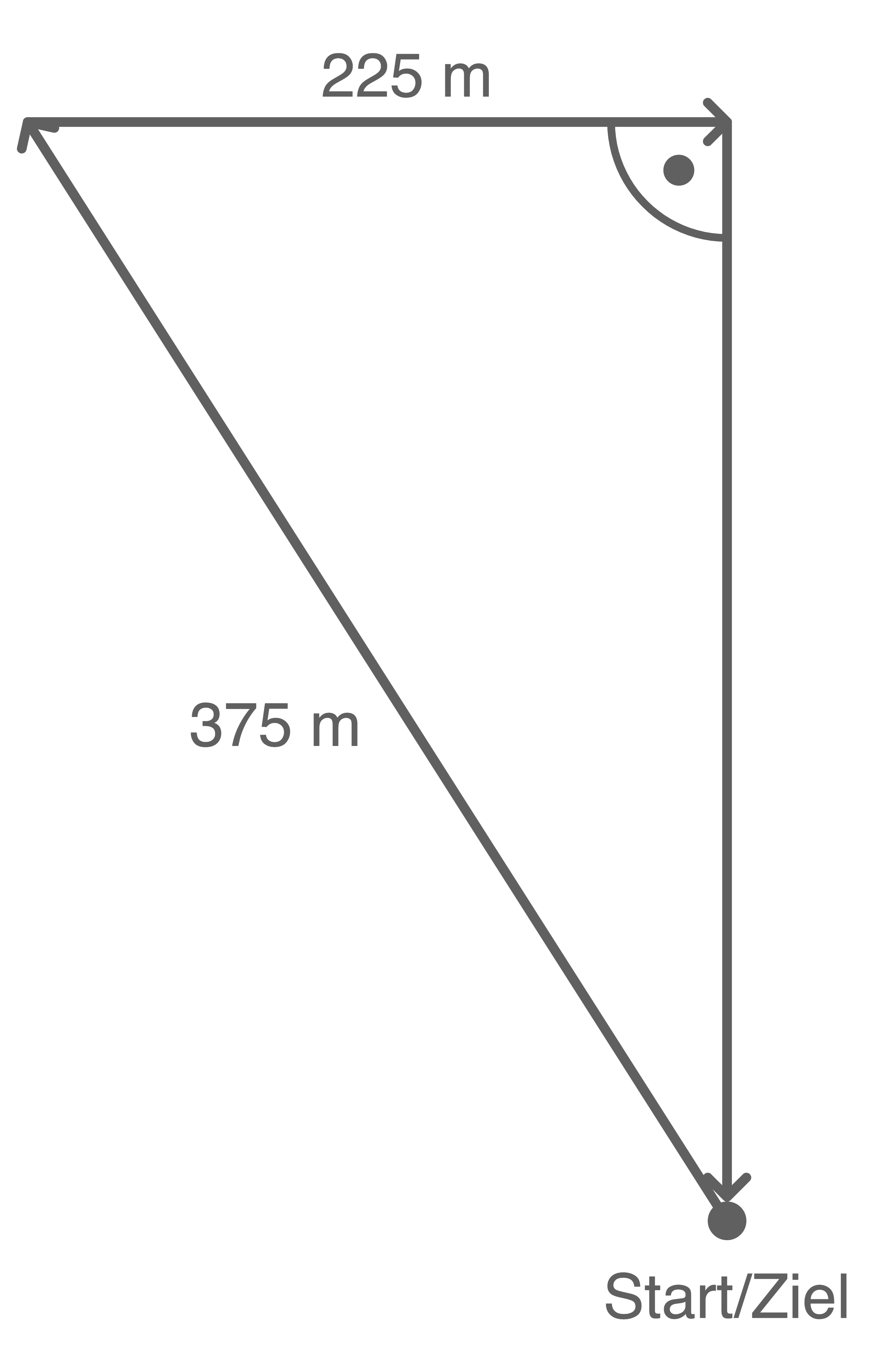
Zeichnung nicht maßstabsgetreu!
(2 Pkt.)
c)
Das Bild zeigt zwei Laufwege von Sportlern in einem Leichtathletikstadion.
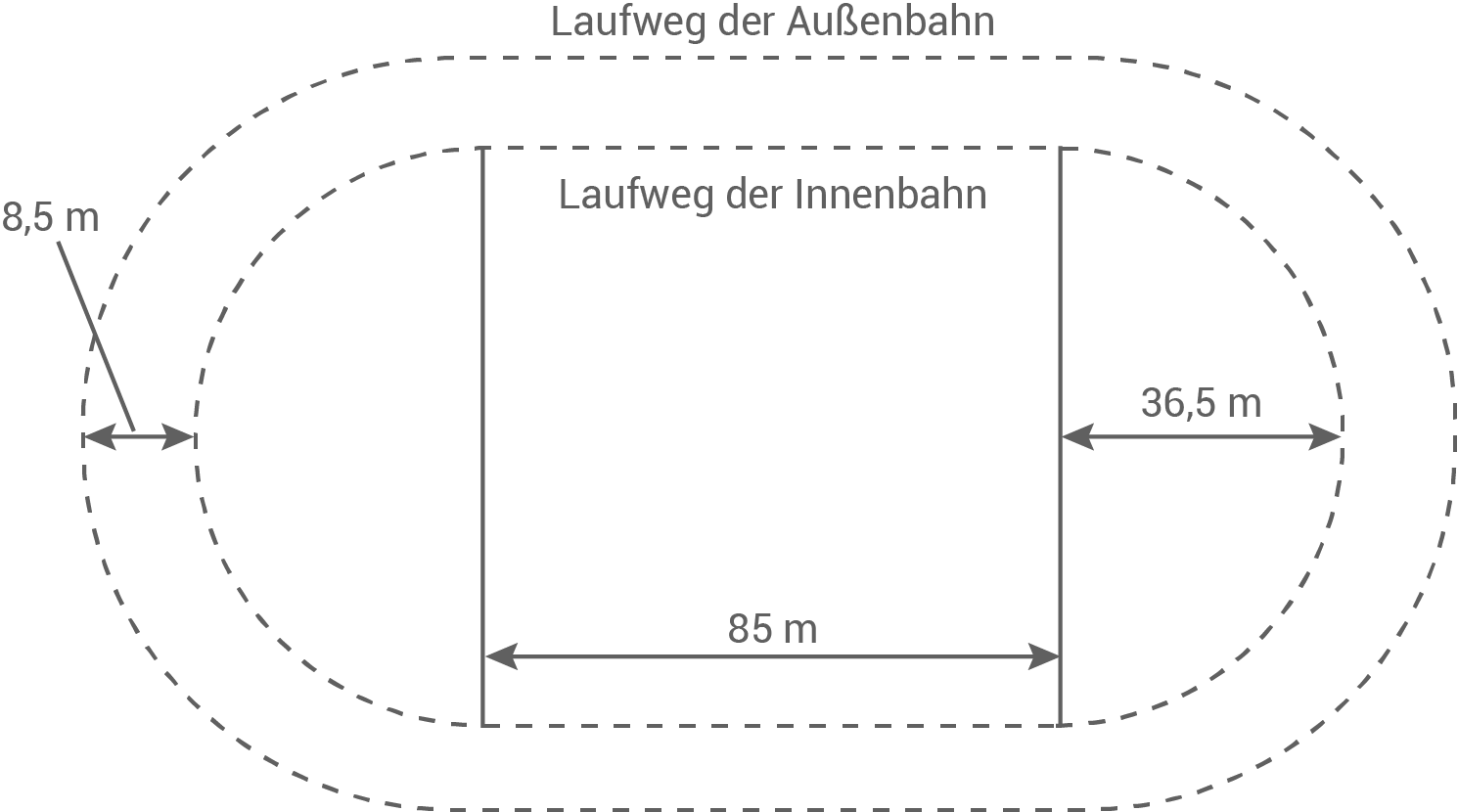 Der Laufweg der Innenbahn ist
Der Laufweg der Innenbahn ist  lang.
lang.
Um wie viel Meter ist der Laufweg der Außenbahn länger?

Zeichnung nicht maßstabsgetreu!
Um wie viel Meter ist der Laufweg der Außenbahn länger?
(2 Pkt.)
Aufgabe 2 – Kochen
a)
Spaghetti Carbonara
Rezept für 4 Personen
Wie viel braucht sie von den einzelnen Zutaten?
Rezept für 4 Personen
Spaghetti
Schinken
Eigelb
Butter
Wie viel braucht sie von den einzelnen Zutaten?
(2 Pkt.)
b)
Antonias Eltern möchten eine neue Küche für  kaufen.
kaufen.
Sie entschließen sich für einen Ratenkauf (Laufzeit 36 Monate).
Dafür verlangt das Küchenstudio einen Aufschlag von auf den Kaufpreis.
Wie viel müssen Antonias Eltern monatlich bezahlen?
auf den Kaufpreis.
Wie viel müssen Antonias Eltern monatlich bezahlen?
Sie entschließen sich für einen Ratenkauf (Laufzeit 36 Monate).
Dafür verlangt das Küchenstudio einen Aufschlag von
(2 Pkt.)
c)
Welchen Durchmesser muss ein  hoher zylinderförmiger Kochtopf mindestens haben, damit 5 Liter Wasser hineinpassen?
hoher zylinderförmiger Kochtopf mindestens haben, damit 5 Liter Wasser hineinpassen?
Runde auf ganze Zentimeter.
Runde auf ganze Zentimeter.
(2 Pkt.)
Aufgabe 3 – Smartphones
a)
Diese Grafik zeigt die Verteilung der Smartphones auf die 5 größten Hersteller.
 Wie viel Prozent der Smartphones entfallen auf den Hersteller C?
Wie viel Prozent der Smartphones entfallen auf den Hersteller C?

(2 Pkt.)
b)
Bei einer Internetseite kann man seine eigene App erstellen.
Gestalte das Startbild deiner App selbst
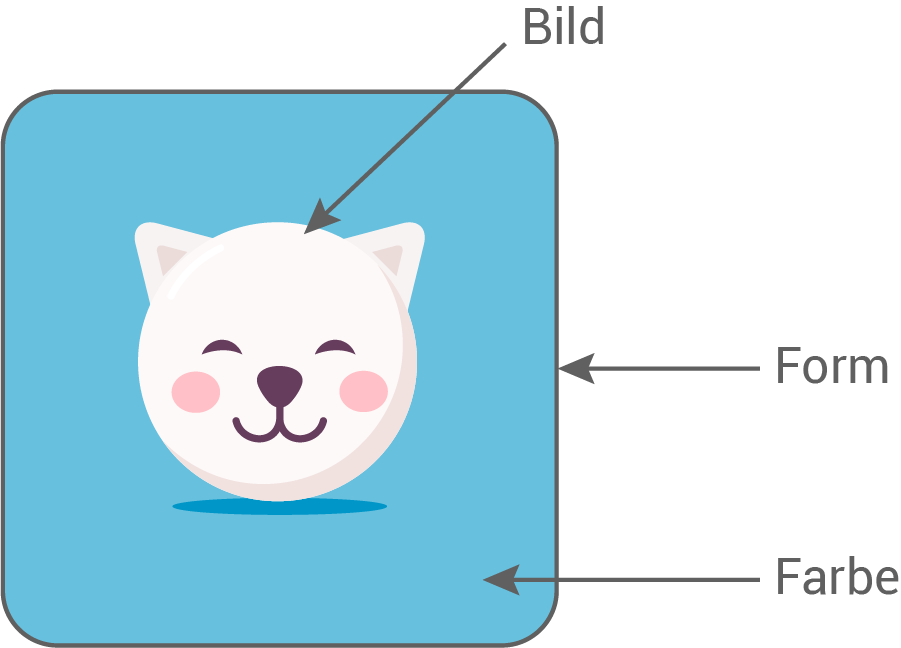 Wähle jeweils aus...
... 2 Formen
Wähle jeweils aus...
... 2 Formen
... 4 Farben
... 3 Bildern eine Möglichkeit aus.

... 4 Farben
... 3 Bildern eine Möglichkeit aus.
- Wie viele verschiedene Kombinationsmöglichkeiten gibt es?
- Die Firma möchte 72 Kombinationsmöglichkeiten anbieten.
Wie viele Bilder, Formen und Farben könnten jetzt zur Auswahl stehen?
(2 Pkt.)
c)
Im Jahr 2012 besaßen 87 Prozent der über 14-Jährigen ein Handy.
40 Prozent dieser Handys waren Smartphones.
Wie viele Smartphones besaßen die über 14-Jährigen?
Bevölkerung in Deutschland 2012:
40 Prozent dieser Handys waren Smartphones.
Wie viele Smartphones besaßen die über 14-Jährigen?
Bevölkerung in Deutschland 2012:
| Alter | Anzahl in Millionen |
|---|---|
| 0 - 14 | |
| 15 - 24 | |
| 25 - 64 | |
| 65 und älter |
(2 Pkt.)
Aufgabe 4 – Schwimmbad
a)
Wie viele Sekunden rutscht man mit einer durchschnittlichen Geschwindigkeit von  ?
?
Runde auf ganze Sekunden.
Runde auf ganze Sekunden.
Superrutsche!
 Rutschspaß
Rutschspaß
(2 Pkt.)
b)
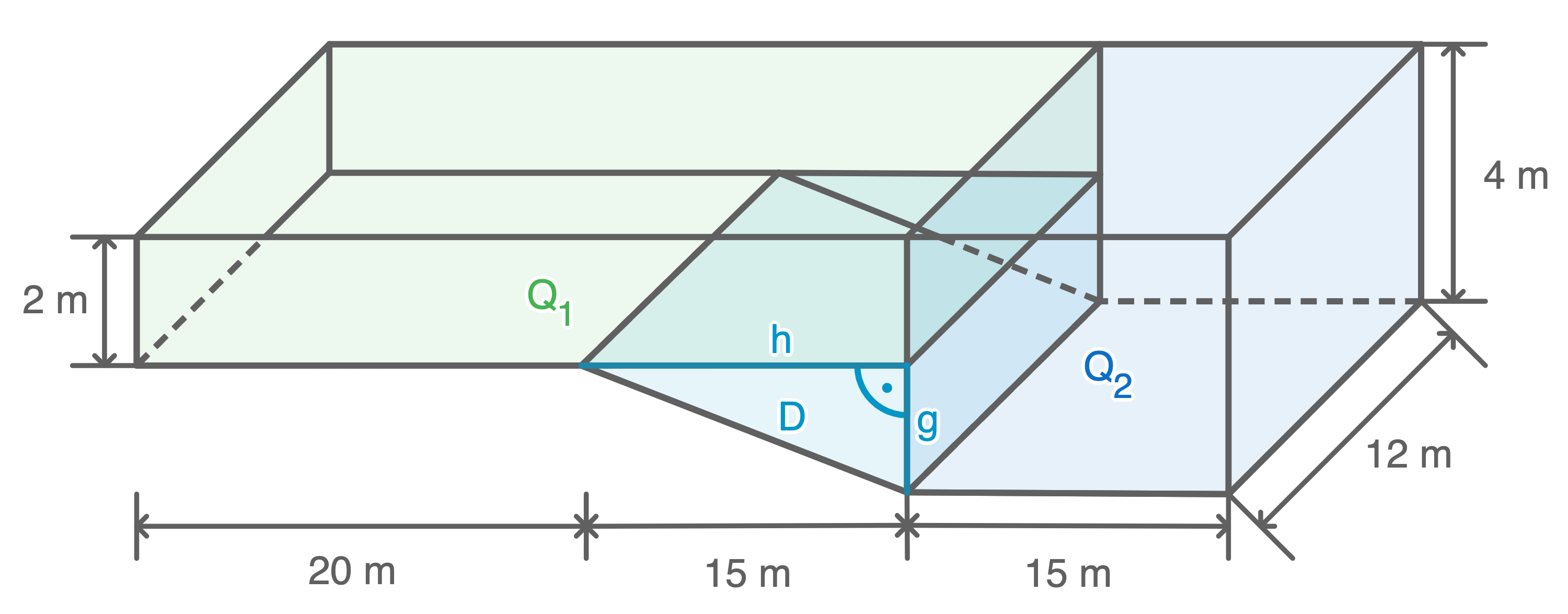
Ein Schwimmbecken hat folgende Maße:
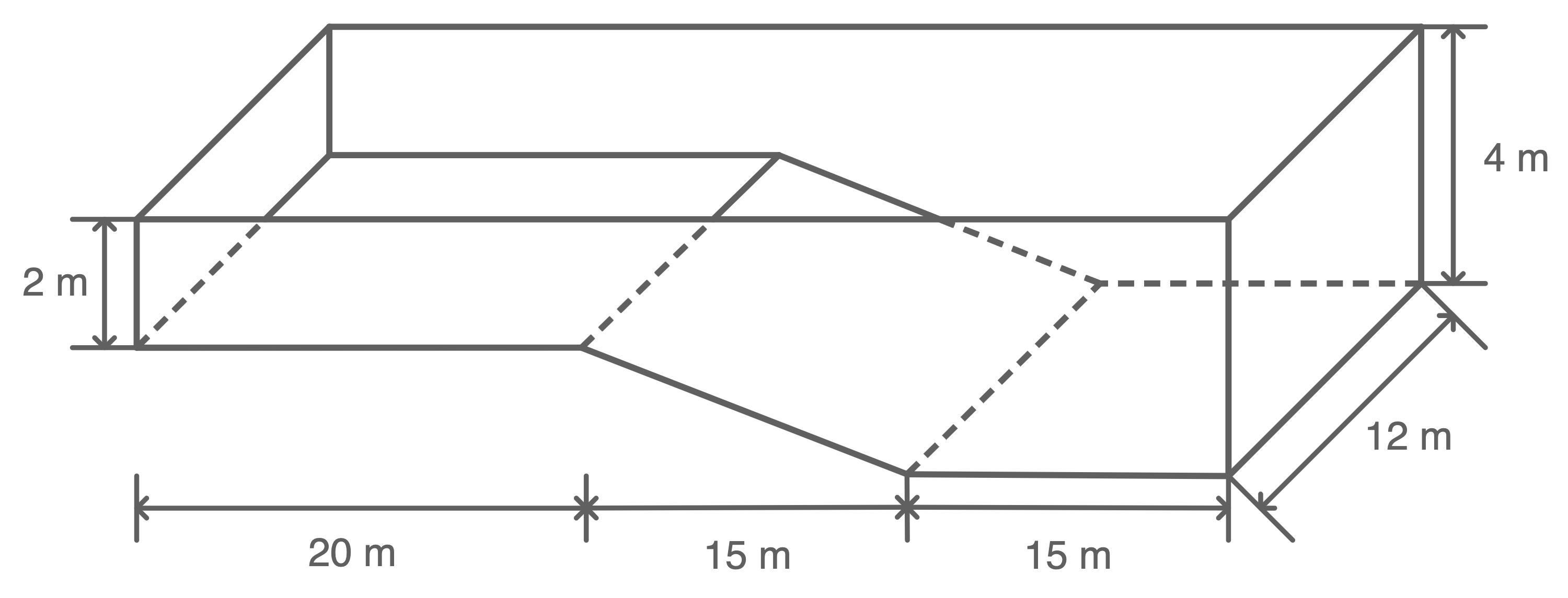 Wie viel
Wie viel  Wasser passen in dieses Becken, wenn es bis zum Rand gefüllt ist?
Wasser passen in dieses Becken, wenn es bis zum Rand gefüllt ist?

Zeichnung nicht maßstabsgetreu!
(2 Pkt.)
c)
Ein Schwimmbecken wurde renoviert und muss neu befüllt werden.
Insgesamt werden Liter Wasser benötigt.
Pumpe 1 läuft 5 Tage, dann wird zur Unterstützung auch noch Pumpe 2 eingesetzt. Beide Pumpen laufen ohne Unterbrechung.
Wie viele Tage dauert das Befüllen des Schwimmbeckens insgesamt?
Liter Wasser benötigt.
Pumpe 1 läuft 5 Tage, dann wird zur Unterstützung auch noch Pumpe 2 eingesetzt. Beide Pumpen laufen ohne Unterbrechung.
Wie viele Tage dauert das Befüllen des Schwimmbeckens insgesamt?
Runde auf ganze Tage. Leistung der Pumpe
Insgesamt werden
Runde auf ganze Tage. Leistung der Pumpe
- Pumpe:
- Pumpe:
(2 Pkt.)
Lösung 1
a)
Wie oft geht Gabriel in einem Vierteljahr joggen?
Ein Vierteljahr hat Monate:
Monate:  Wie viele Kilometer joggt er in einem Vierteljahr?
Wie viele Kilometer joggt er in einem Vierteljahr?
 Gabriel joggt in einem Vierteljahr also
Gabriel joggt in einem Vierteljahr also 
Ein Vierteljahr hat
b)
Die fehlende Streckenlänge  kann mithilfe des Satz des Pythagoras berechnet werden:
kann mithilfe des Satz des Pythagoras berechnet werden:
![\(\begin{array}[t]{rll}
a^2+b^2&=&c^2 &\quad \scriptsize \mid\;-b^2 \\[5pt]
a^2&=&c^2-b^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
a&=&\sqrt{c^2-b^2} \\[5pt]
a&=&\sqrt{(375\,\text{m})^2-(225\,\text{m})^2} \\[5pt]
a&=&300\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/72ad56ebc8ed52e875a6cfb86d5f087250b812757ed2e1c76214c15e42fc904d_light.svg) Gesamtlänge der Strecke:
Gesamtlänge der Strecke:  Onurs Schwimmstrecke hat eine Länge von
Onurs Schwimmstrecke hat eine Länge von 
c)
Der Laufweg setzt sich zusammen aus dem Laufweg oben, Laufweg unten und den beiden Halbkreisen links und rechts (= ein ganzer Kreis).
Kreisumfang berechnen
Die beiden Halbkreise entsprechen dem Umfang eines Kreises.
Dafür wird zunächst der Radius benötigt: Damit folgt für den Umfang:
Damit folgt für den Umfang:
![\(\begin{array}[t]{rll}
u&=&2\pi\cdot r \\[5pt]
u&=&2\pi\cdot 45\,\text{m} \\[5pt]
u&\approx&283\,\text{m} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2a04057922390de486bf4a890a16347250f7edd709a0b07befde1dc1c11d4fd6_light.svg) Länge des Laufwegs der Außenbahn berechnen
Länge des Laufwegs der Außenbahn berechnen
![\(\begin{array}[t]{rll}
s_{\text{außen}}&=& 85\,\text{m}+85\,\text{m}+283\,\text{m} \\[5pt]
s_{\text{außen}}&=& 453\,\text{m} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/18871620149126445a33c323f517977e9d25a7a80e09e92048c5f5ae9bd12a6b_light.svg) Um wie viel Meter ist der Laufweg der Außenbahn länger?
Um wie viel Meter ist der Laufweg der Außenbahn länger?
 Der Laufweg der Außenbahn ist um
Der Laufweg der Außenbahn ist um  länger.
länger.
Dafür wird zunächst der Radius benötigt:
Lösung 2
a)
Dreisatz für die Spaghetti




![\(\begin{array}{rcl}
4\,\text{Personen} & \mathrel{\widehat{=}}& 400\,\text{g}\\[5pt]
1\,\text{Person} & \mathrel{\widehat{=}}& 100\,\text{g}\\[5pt]
7\,\text{Personen} & \mathrel{\widehat{=}}& 700\,\text{g}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/00993619513d20b16883f10b7d7571abfdd7f2535a242fe8775b0986741313db_light.svg)



 Dreisatz für den Schinken
Dreisatz für den Schinken




![\(\begin{array}{rcl}
4\,\text{Personen} & \mathrel{\widehat{=}}& 250\,\text{g}\\[5pt]
1\,\text{Person} & \mathrel{\widehat{=}}& 62,5\,\text{g}\\[5pt]
7\,\text{Personen} & \mathrel{\widehat{=}}& 437,5\,\text{g}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2b53a494d97d527ec8041269d23373486676b6a5ae0f188438746bb47fd95a8f_light.svg)



 Dreisatz für das Eigelb
Dreisatz für das Eigelb




![\(\begin{array}{rcl}
4\,\text{Personen} & \mathrel{\widehat{=}}& 4\\[5pt]
1\,\text{Person} & \mathrel{\widehat{=}}& 1\\[5pt]
7\,\text{Personen} & \mathrel{\widehat{=}}& 7\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/91c05c26ead2bfe49441b1c387821ae5384ea80b015a51964ca353a4a551f222_light.svg)



 Dreisatz für die Butter
Dreisatz für die Butter




![\(\begin{array}{rcl}
4\,\text{Personen} & \mathrel{\widehat{=}}& 60\,\text{g}\\[5pt]
1\,\text{Person} & \mathrel{\widehat{=}}& 15\,\text{g}\\[5pt]
7\,\text{Personen} & \mathrel{\widehat{=}}& 105\,\text{g}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a5a1134a6223920247c05d024a9e55a05d569f4aad6072f0220f65aa92dd0965_light.svg)



 Antonia braucht für
Antonia braucht für  Personen:
Personen:
Spaghetti
Schinken
Eigelb
Butter
b)
Küchenpreis mit Aufschlag berechnen




![\(\begin{array}{rcl}
100\,\%& \mathrel{\widehat{=}}&10\,500\,€\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 105\,€\\[5pt]
105\,\% & \mathrel{\widehat{=}}& 11\,025\,€
\end{array}\)](https://www.schullv.de/resources/formulas/82bf9bbf593adc499f7e5b591962b2d05740fa0490edc7158785cbf8147b4c53_light.svg)



 Monatliche Rate berechnen
Monatliche Rate berechnen
 Antonias Eltern müssen monatlich
Antonias Eltern müssen monatlich  bezahlen.
bezahlen.
c)
Damit mit der Volumen-Angabe gerechnet werden kann, wird diese in Kubikzentimeter umgerechnet:
 Um den Durchmesser des Kochtopfs zu berechnen, wird die Formel zur Berechnung des Volumens nach
Um den Durchmesser des Kochtopfs zu berechnen, wird die Formel zur Berechnung des Volumens nach  umgestellt:
umgestellt:
![\(\begin{array}[t]{rll}
V&=&r^2\cdot \pi\cdot h &\quad \scriptsize \mid\;:\pi \\[5pt]
\dfrac{V}{\pi}&=&r^2\cdot h &\quad \scriptsize \mid\;:h \\[5pt]
\dfrac{V}{\pi\cdot h}&=&r^2& \\[5pt]
r^2&=&\dfrac{V}{\pi\cdot h}&\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
r&=&\sqrt{\dfrac{V}{\pi\cdot h}} \\[5pt]
r&=&\sqrt{\dfrac{5\,000\,\text{cm}^3}{\pi\cdot 16\,\text{cm}}} \\[5pt]
r&\approx&10,0\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/5cf464efe02d2e434f60ede20b73877ac059298739e980bad2c295ef2818786b_light.svg) Daraus folgt für den Durchmesser:
Daraus folgt für den Durchmesser:  Der Topf muss also einen Durchmesser von
Der Topf muss also einen Durchmesser von  haben.
haben.
Lösung 3
a)
Die Grafik zeigt insgesamt  Kästchen. Davon stehen
Kästchen. Davon stehen  Kästchen für den Hersteller C.
Damit lässt sich der Prozentsatz berechnen:
Kästchen für den Hersteller C.
Damit lässt sich der Prozentsatz berechnen: 
 der Smartphones entfallen auf den Hersteller C.
der Smartphones entfallen auf den Hersteller C.
b)
Wie viele verschiedene Kombinationsmöglichkeiten gibt es?
Um den Überblick über alle möglichen Kombinationen zu bewahren, hilft das Erstellen eines Baumdiagramms:
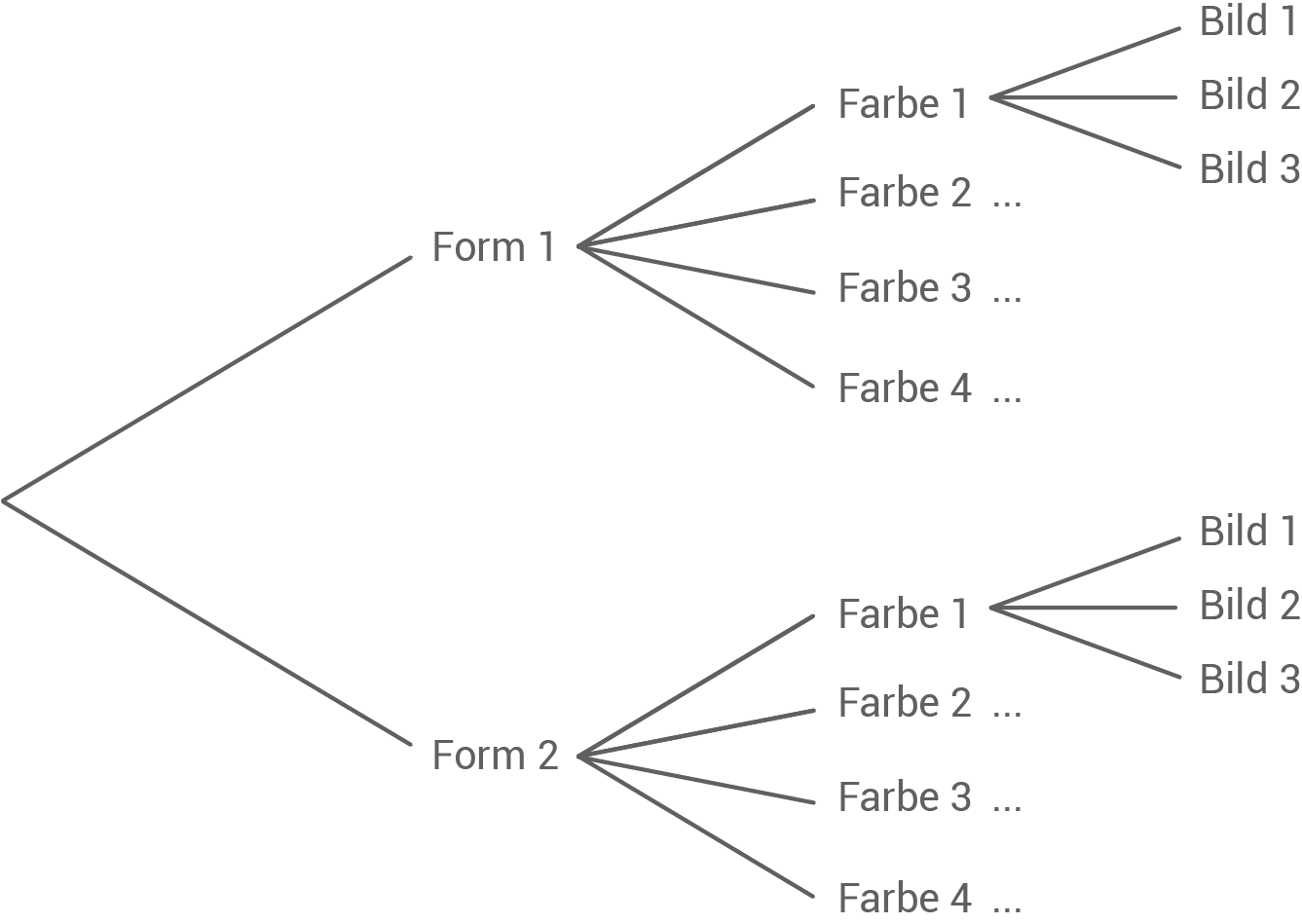 Zu jeder Farbe gehören drei Bild-Pfade. Aus Platzgründen sind in dem Baumdiagramm nur
Zu jeder Farbe gehören drei Bild-Pfade. Aus Platzgründen sind in dem Baumdiagramm nur  Bild-Pfade eingezeichnet.
Um die Anzahl aller Möglichkeiten zu ermitteln, müssen alle Bild-Pfade gezählt werden: Es gibt also
Bild-Pfade eingezeichnet.
Um die Anzahl aller Möglichkeiten zu ermitteln, müssen alle Bild-Pfade gezählt werden: Es gibt also  Möglichkeiten.
Wie viele Bilder, Formen und Farben könnten jetzt zur Auswahl stehen?
Lösungsweg 1: Die Anzahl der Formen wird verändert
Die Unbekannte
Möglichkeiten.
Wie viele Bilder, Formen und Farben könnten jetzt zur Auswahl stehen?
Lösungsweg 1: Die Anzahl der Formen wird verändert
Die Unbekannte  steht für die neue Anzahl der Formen:
steht für die neue Anzahl der Formen:
![\(\begin{array}[t]{rll}
x\cdot 4\cdot 3&=&72 &\quad \scriptsize \mid\;:4 \\[5pt]
x\cdot 3&=&18 &\quad \scriptsize \mid\;:3 \\[5pt]
x&=&6
\end{array}\)](https://www.schullv.de/resources/formulas/a6d6377175a13e940ca24489a2c6396c1fcefdf33ffb0f50fd1539391707e0a0_light.svg) Für 72 Kombinationsmöglichkeiten könnten 6 Formen, 4 Farben und 3 Bilder zur Verfügung stehen.
Lösungsweg 2: Die Anzahl der Farben wird verändert
Die Unbekannte
Für 72 Kombinationsmöglichkeiten könnten 6 Formen, 4 Farben und 3 Bilder zur Verfügung stehen.
Lösungsweg 2: Die Anzahl der Farben wird verändert
Die Unbekannte  steht für die neue Anzahl der Farben:
steht für die neue Anzahl der Farben:
![\(\begin{array}[t]{rll}
2\cdot y\cdot 3&=&72 &\quad \scriptsize \mid\;:2 \\[5pt]
y\cdot 3&=&36 &\quad \scriptsize \mid\;:3 \\[5pt]
y&=&12
\end{array}\)](https://www.schullv.de/resources/formulas/4b1c212dc4d414524d2f658a3b20002b4ef7a4067c11abd582e57a5824170b02_light.svg) Für 72 Kombinationsmöglichkeiten könnten 2 Formen, 12 Farben und 3 Bilder zur Verfügung stehen.
Lösungsweg 3: Die Anzahl der Bilder wird verändert
Die Unbekannte
Für 72 Kombinationsmöglichkeiten könnten 2 Formen, 12 Farben und 3 Bilder zur Verfügung stehen.
Lösungsweg 3: Die Anzahl der Bilder wird verändert
Die Unbekannte  steht für die neue Anzahl der Bilder:
steht für die neue Anzahl der Bilder:
![\(\begin{array}[t]{rll}
2\cdot 4\cdot z&=&72 &\quad \scriptsize \mid\;:2 \\[5pt]
4\cdot z&=&36 &\quad \scriptsize \mid\;:4 \\[5pt]
z&=&9
\end{array}\)](https://www.schullv.de/resources/formulas/4e336c8fbd0f68ee36eaa3e80f96ca98e9c8414f06dfa906a3495b8590157d60_light.svg) Für 72 Kombinationsmöglichkeiten könnten 2 Formen, 4 Farben und 9 Bilder zur Verfügung stehen.
Hinweis: Bei Lösungsweg 1, 2 und 3 wurde jeweils eine der drei Komponenten geändert. Es können auch mehrere Komponenten geändert werden, um auf 72 Kombinationsmöglichkeiten zu kommen.
Für 72 Kombinationsmöglichkeiten könnten 2 Formen, 4 Farben und 9 Bilder zur Verfügung stehen.
Hinweis: Bei Lösungsweg 1, 2 und 3 wurde jeweils eine der drei Komponenten geändert. Es können auch mehrere Komponenten geändert werden, um auf 72 Kombinationsmöglichkeiten zu kommen.

c)
Anzahl aller über 14-Jährigen im Jahr 2020 berechnen
 Anzahl der Handys berechnen
Anzahl der Handys berechnen
 der über 14-Jährigen besaßen 2012 ein Smartphone.
der über 14-Jährigen besaßen 2012 ein Smartphone.
Lösung über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 69,88\,\text{Mio.}\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{69,88}{100}\,\text{Mio.}\\[5pt]
87\,\% & \mathrel{\widehat{=}}& \dfrac{69,88}{100}\cdot 87\,\text{Mio.}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/1c6c256a76daa8d5421fa73b1b384726665d141ce27e149e1cafebe348b4212e_light.svg)





Lösung über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} \\[5pt]
P&=&\dfrac{69,88\,\text{Mio.}\cdot 87}{100} \\[5pt]
P&=&60,7956\,\text{Mio.} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/10d63c9e871d764f139a9d4cb4fff6d342e8531f4cdffc9127828339ec5ed89c_light.svg)
Anzahl der Smartphones berechnen
Lösung über den Dreisatz




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 60,7956\,\text{Mio.}\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{60,7956}{100}\,\text{Mio.}\\[5pt]
40\,\% & \mathrel{\widehat{=}}& \dfrac{60,7956}{100}\cdot 40\,\text{Mio.}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/95924280993d5f865eb48c0517fc1035b9a474397dd31748b14a17da63e1c50c_light.svg)





Lösung über die Formel
![\(\begin{array}[t]{rll}
P&=&\dfrac{G\cdot p}{100} \\[5pt]
P&=&\dfrac{60,7956\,\text{Mio.}\cdot 40}{100} \\[5pt]
P&\approx& 24,3\,\text{Mio.} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7abd0002487c5ac4de5c08500af31b89f20d7be149a6d567708a0b25dac09070_light.svg)
Etwa Lösung 4
a)
Um die Dauer zu berechnen, wird die Formel zur Berechnung der Geschwindigkeit nach  umgestellt:
umgestellt:
![\(\begin{array}[t]{rll}
v&=& \dfrac{s}{t}\quad\quad\quad\quad\scriptsize \mid\;\cdot t \\[5pt]
v\cdot t&=& s\quad\quad\quad\quad\quad\scriptsize \mid\;:v \\[5pt]
t&=& \dfrac{s}{v}\\[5pt]
t&=& \dfrac{0,18\,\text{km}}{15\dfrac{\text{km}}{\text{h}}}\\[5pt]
t&=& 0,012\,\text{h}\\[5pt]
t&=& 60\cdot 0,012\,\text{min}=0,72\,\text{min}\\[5pt]
t&=& 60\cdot 0,72\,\text{sec}=43,2\,\text{sec}\approx 43\,\text{sec}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d5d3bf59f5300a7c0bfaeb6bca1b96e6b80ce667008234bd6022c926c5bf53ae_light.svg) Mit einer durchschnittlichen Geschwindigkeit von
Mit einer durchschnittlichen Geschwindigkeit von  rutscht man etwa
rutscht man etwa 
b)
c)
Gepumptes Wasser nach 5 Tagen:  Leistung der beiden Pumpen:
Leistung der beiden Pumpen:  Nach 5 Tagen werden noch
Nach 5 Tagen werden noch  Liter Wasser benötigt.
Mit diesen Angaben kann eine Gleichung aufgestellt werden. Dabei steht die Unbekannte
Liter Wasser benötigt.
Mit diesen Angaben kann eine Gleichung aufgestellt werden. Dabei steht die Unbekannte  für die Anzahl der Tage, die die Pumpe nach Ablauf der 5 Tage noch laufen muss:
für die Anzahl der Tage, die die Pumpe nach Ablauf der 5 Tage noch laufen muss:
![\(\begin{array}[t]{rll}
x\cdot 24\cdot 6\,000&=&1\,580\,000 &\quad \scriptsize \mid\;:24 \\[5pt]
x\cdot 6\,000&=&\dfrac{1\,580\,000}{24} &\quad \scriptsize \mid\;:6\,000 \\[5pt]
x&=&\dfrac{1\,580\,000}{24\cdot 6\,000\,} & \\[5pt]
x&\approx&11 &
\end{array}\)](https://www.schullv.de/resources/formulas/a4cc80ec63f8439dd84b0326b52ef885506dc20528d554699e927afd529e1c54_light.svg) Es dauert also insgesamt
Es dauert also insgesamt  Tage, das Schwimmbecken zu befüllen.
Tage, das Schwimmbecken zu befüllen.