Wahlpflichtaufgaben

Aufgabe 1 – Luftschiff

Die „Hindenburg“ war das größte Luftschiff der Geschichte. Ermittle die Länge des Luftschiffes.

(2 Pkt.)

Ein Luftschiff hatte eine Reisegeschwindigkeit von durchschnittlich $115 \frac{\,\text{km}}{\,\text{h}}.$
Wie lange benötigte es für die $11\,247\,\text{km}$ von Friedrichshafen nach Tokio?
Gib das Ergebnis in Stunden und Minuten an.

(2 Pkt.)

Die aufgelisteten 5 Etappen wurden 1929 als „Weltumrundung“ bezeichnet.

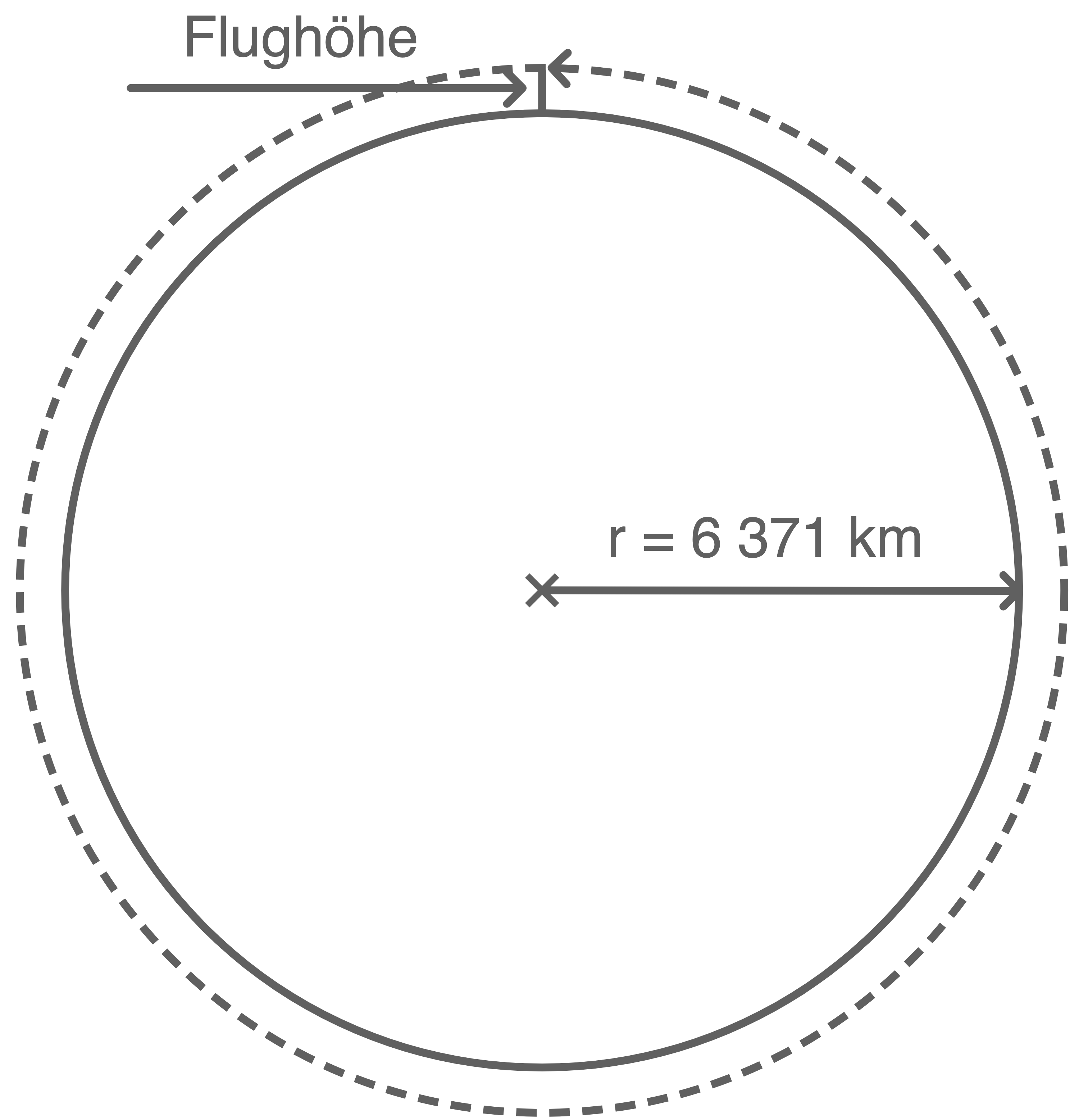Würden die Kilometer der 5 Etappen zusammengenommen ausreichen, um mit einem Flugzeug in $11 \,\text{km}$ Höhe die Erde zu umfliegen?
Begründe rechnerisch.

(2 Pkt.)

Aufgabe 2 – Wasser

Gib den durchschnittlichen Wasserverbrauch für die Toilettenspülung in Prozent an.

(2 Pkt.)

Der abgebildete Behälter ist bereits teilweise mit Wasser gefüllt.

Zeichnung nicht maßstabsgetreu

Felix hat ein quaderförmiges Gefäß mit den Maßen $6 \,\text{cm}$ x $6 \,\text{cm}$ x $4 \,\text{cm}$ , das randvoll mit Wasser gefüllt ist.
Passt dieses Wasser noch in den Behälter?
Begründe rechnerisch.

(2 Pkt.)

Unter einen gleichmäßig tropfenden Wasserhahn wird ein leerer $10$ -Liter-Eimer geschoben. Um $10$ Uhr befinden sich $2,0$ Liter Wasser im Eimer, $90$ Minuten später sind es $4,4$ Liter.

Um wie viel Uhr ist der Eimer voll?
Zu welcher Uhrzeit wurde der leere Eimer unter den Wasserhahn gestellt?

(2 Pkt.)

Aufgabe 3 – Hausbau

Eine quaderförmige Baugrube wird ausgehoben.
Maße: Länge $15 \,\text{m},$ Breite $10 \,\text{m},$ Höhe $2,50 \,\text{m}$
Pro Fahrt kann ein Lkw $7 \,\text{m}^3$ dieser Erde transportieren.

Wie oft muss der Lkw mindestens fahren, um die gesamte Erde abzutransportieren?

(2 Pkt.)

Um ihr Haus bauen zu können, muss Familie Häberle einen Kredit in Höhe von $200\,000 \,€$ bei einer Bank aufnehmen.

Wie viel Euro muss Familie Häberle im ersten Monat an Zinsen zahlen?

(2 Pkt.)

Die graue Dachfläche des Hauses soll gedeckt werden.
Wie groß ist diese Dachfläche?

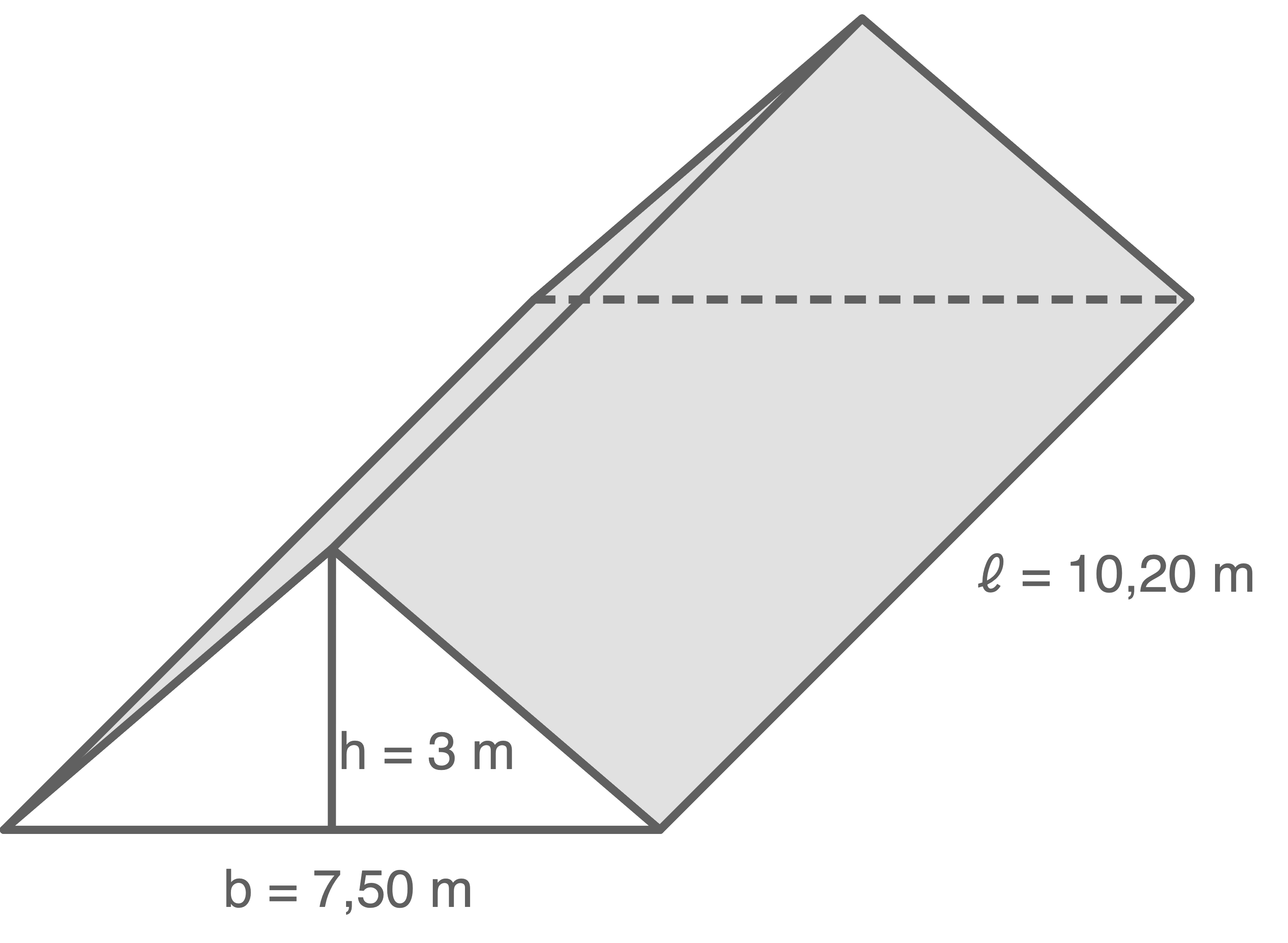
hauptschulabschluss mathe 2018 baden-württemberg

Zeichnung nicht maßstabsgetreu

(2 Pkt.)

Aufgabe 4 – Neue Eurobanknoten

Die Tabelle gibt Auskunft über die Anzahl und den Wert der 2014 im Umlauf befindlichen Eurobanknoten.

Auswahl an Eurobanknoten	Anzahl der Eurobanknoten	Wert
$5 \,€$		$8,30$ Mrd. $\,€$
$10 \,€$	$2\,112$ Mio.	$21,12$ Mrd. $\,€$
$50 \,€$	$7\,615$ Mio.
$200 \,€$	$202$ Mio.	$40,40$ Mrd. $\,€$

Berechne die fehlenden Angaben.

(2 Pkt.)

Durchschnittlich sind $12$ gefälschte Geldscheine je $10\,000$ Einwohner im Umlauf.
Wie viele gefälschte Geldscheine sind es in Mannheim $(316\,000$ Einwohner) durchschnittlich?

(2 Pkt.)

Seit April 2017 gibt es neue $50$ -Euro-Scheine. Am Anfang wurden $5,4$ Milliarden Scheine in Umlauf gebracht.
Nebeneinandergelegt würden diese Scheine die Fläche der Stadt Weinheim bedecken.

Welche Fläche hat diese Stadt?
Gib das Ergebnis in $\text{km}^2$ an.

Zeichnung nicht maßstabsgetreu

(2 Pkt.)

Lösung 1

Durch Abmessen erhält man folgende Längen:

Luftschiff: $3,6\,\text{cm}$
Airbus: $12,1\,\text{cm}$

Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

Da die wirkliche Länge des Airbus gegeben ist, kann mithilfe des Dreisatzes auch die wirkliche Länge des Luftschiffes ermittelt werden:

$:3,6$

$\cdot 12,1$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 3,6\,\text{cm} & \mathrel{\widehat{=}}& 72,7\,\text{m}\\[5pt] 1\,\text{cm} & \mathrel{\widehat{=}}& \dfrac{72,7}{3,6}\,\text{m}\\[5pt] 12,1\,\text{cm} & \mathrel{\widehat{=}}& \dfrac{72,7}{3,6}\cdot 12,1\,\text{m} \end{array}$

$:3,6$

$\cdot 12,1$

$\dfrac{72,7}{3,6}\cdot 12,1\,\text{m}\approx 244,35\,\text{m}$

Das Luftschiff war etwa $244,35\,\text{m}$ lang.

Die Formel zur Berechnung der Geschwindigkeit lautet: $v=\dfrac{s}{t}.$ Da in der Aufgabenstellung die Zeit gesucht ist, muss die Formel nach $t$ umgestellt werden:

$\begin{array}[t]{rll} v&=& \dfrac{s}{t}&\quad \scriptsize \mid\;\cdot t \\[5pt] v\cdot t&=& s&\quad \scriptsize \mid\;:v \\[5pt] t&=& \dfrac{s}{v}\\[5pt] t&=& \dfrac{11\,247\,\text{km}}{115 \frac{\,\text{km}}{\,\text{h}}} \\[5pt] t&=& 97,8\,\text{h} \\[5pt] \end{array}$

Nun müssen nur noch die $0,8\,\text{h}$ in Minuten umgerechnet werden:

$\cdot 0,8$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 1\,\text{h} & \mathrel{\widehat{=}}& 60\,\text{min}\\[5pt] 0,8\,\text{h} & \mathrel{\widehat{=}}& 48\,\text{min}\\[5pt] \end{array}$

$\cdot 0,8$

Das Luftschiff brauchte $97\,\text{h}\, 48\,\text{min}$ für die Strecke.

Umfang des Kreises um die Erde berechnen

Der Radius dieses Kreises setzt sich aus dem Radius der Erde $r$ und der Flughöhe $h$ zusammen:
$\begin{array}[t]{rll} r_{\text{Kreis}}&=&r+h\\[5pt] r_{\text{Kreis}}&=&6\,371\,\text{km}+11\,\text{km}\\[5pt] r_{\text{Kreis}}&=&6\,382\,\text{km} \end{array}$

Damit kann nun der Umfang berechnet werden:
$\begin{array}[t]{rll} u&=& 2\cdot \pi\cdot r_{\text{Kreis}} \\[5pt] u&=& 2\cdot \pi\cdot 6\,382\,\text{km} \\[5pt] u&\approx& 40\,099\,\text{km} \\[5pt] \end{array}$

Länge der 5 Etappen berechnen

$s=8\,500\,\text{km}+11\,247\,\text{km}$ $+9\,652\,\text{km}+4\,822\,\text{km}$ $+8\,478\,\text{km}=42\,699\,\text{km}$

Da die 5 Etappen zusammengenommen länger sind als der Umfang des Kreises um die Erde, würden sie für eine Umrundung der Erde ausreichen.

Lösung 2

Lösung über den Dreisatz

$:125$

$\cdot 34$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 100\,\% & \mathrel{\widehat{=}}& 125\,\text{l} \\[5pt] 0,8\,\% & \mathrel{\widehat{=}}& 1\,\text{l} \\[5pt] 27,2\,\% & \mathrel{\widehat{=}}& 34\,\text{l} \\[5pt] \end{array}$

$:125$

$\cdot 34$

Lösung über die Formel

$\begin{array}[t]{rll} p\,\%&=& \dfrac{P\cdot 100}{G}\,\% \\[5pt] p\,\%&=& \dfrac{34\cdot 100}{125}\,\% \\[5pt] p\,\%&=& 27,2\,\% \\[5pt] \end{array}$

Der durchschnittliche Wasserverbrauch für die Toilettenspülung beträgt $27,2\,\%.$

Wie viel Wasser passt noch in den Behälter?

Hierfür wird das Volumen des markierten Quaders berechnet:

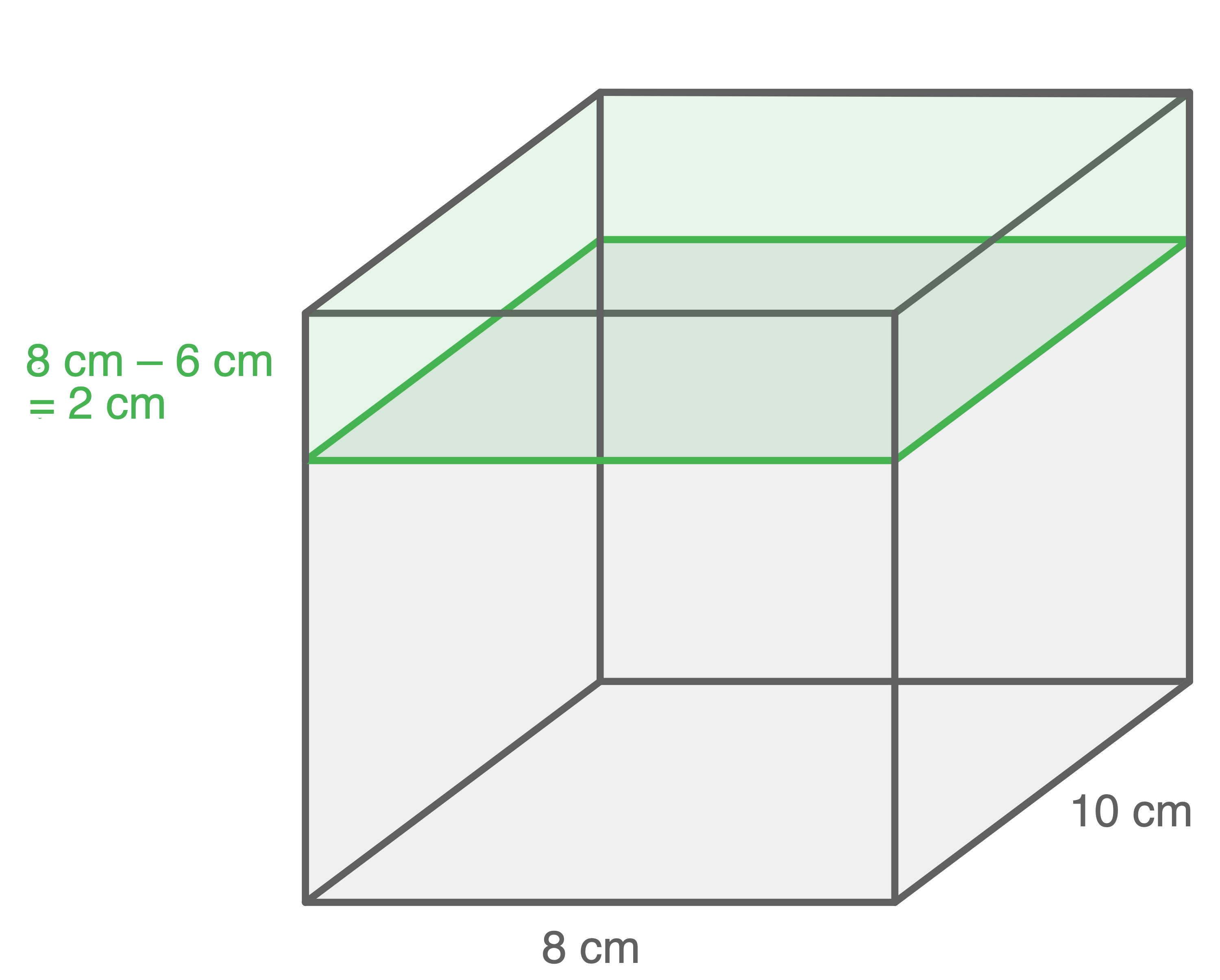
$\begin{array}[t]{rll} V_1&=&a\cdot b\cdot c \\[5pt] V_1&=&8\,\text{cm}\cdot 2\,\text{cm}\cdot 10\,\text{cm} \\[5pt] V_1&=&160\,\text{cm}^3 \\[5pt] \end{array}$

Wie viel Wasser ist in Felix Gefäß drin?

$\begin{array}[t]{rll} V_2&=& a\cdot b\cdot c \\[5pt] V_2&=& 6\,\text{cm}\cdot 6\,\text{cm}\cdot 4\,\text{cm} \\[5pt] V_2&=& 144\,\text{cm}^3 \end{array}$

Somit passt das Wasser von Felix noch in den bereits gefüllten Behälter.

Um wie viel Uhr ist der Eimer voll?

Tropfen pro 90 Minuten: $4,4\,\text{l}-2\,\text{l}=2,4\,\text{l}$

Um 10 Uhr ist der Eimer mit $2\,\text{l}$ gefüllt.
Damit der Eimer voll ist, fehlen also noch $10\,\text{l}-2\,\text{l}=8\,\text{l}.$

Mit diesen Angaben kann der Dreisatz aufgestellt werden:

$:2,4$

$\cdot 8$

$\begin{array}{rcl} 2,4\,\text{l} & \mathrel{\widehat{=}}& 90\,\text{min}\\[5pt] 1\,\text{l} & \mathrel{\widehat{=}}& 37,5\,\text{min}\\[5pt] 8\,\text{l} & \mathrel{\widehat{=}}& 300\,\text{min} \end{array}$

$:2,4$

$\cdot 8$

Ab 10 Uhr braucht es noch $300\,\text{min}:60=5\,\text{h}$ bis der Eimer gefüllt ist. Somit ist dann 15 Uhr.

Zu welcher Uhrzeit wurde der leere Eimer unter den Wasserhahn gestellt?

Um 10 Uhr ist der Eimer mit $2\,\text{l}$ gefüllt. Es muss also berechnet werden, wie lange es gebraucht hat, die $2\,\text{l}$ zu erreichen:

$:2,4$

$\cdot 2$

$\begin{array}{rcl} 2,4\,\text{l} & \mathrel{\widehat{=}}& 90\,\text{min}\\[5pt] 1\,\text{l} & \mathrel{\widehat{=}}& 37,5\,\text{min}\\[5pt] 2\,\text{l} & \mathrel{\widehat{=}}& 75\,\text{min} \end{array}$

$:2,4$

$\cdot 2$

Es hat also $75\,\text{min}:60=1,25\,\text{h}$ gedauert bis die $2\,\text{l}$ erreicht waren. Der Eimer wurde somit um 8:45 Uhr unter den Wasserhahn gestellt.

Lösung 3

Volumen der Baugrube berechnen

$\begin{array}[t]{rll} V&=&a\cdot b\cdot c \\[5pt] V&=&15\,\text{m}\cdot 10\,\text{m}\cdot 2,5\,\text{m} \\[5pt] V&=&375\,\text{m}^3 \\[5pt] \end{array}$

Anzahl der Fahrten

$375\,\text{m}^3:7\,\text{m}^3\approx 54$

Der Lkw muss mindestens 54-mal fahren, um die gesamte Erde abzutransportieren.

Lösungsweg über den Dreisatz

Jahreszinsen berechnen

$:100$

$\cdot 0,96$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 100\,\% & \mathrel{\widehat{=}}& 200\,000\,€\\[5pt] 1\,\% & \mathrel{\widehat{=}}& 2\,000\,€\\[5pt] 0,96\,\% & \mathrel{\widehat{=}}& 1\,920\,€ \end{array}$

$:100$

$\cdot 0,96$

Monatszinsen berechnen

Ein Jahr hat 12 Monate. Somit müssen die Jahreszinsen noch durch 12 dividiert werden: $1\,920\,€:12=160\,€$

Lösungsweg über die Formel

$\begin{array}[t]{rll} Z&=&\dfrac{K\cdot p\cdot m}{100\cdot 12} \\[5pt] Z&=&\dfrac{200\,000\,€\cdot 0,96\cdot 1}{100\cdot 12} \\[5pt] Z&=&160\,€ \\[5pt] \end{array}$

Im ersten Monat muss Familie Häberle $160\,€$ Zinsen bezahlen.

Die Dachfläche setzt sich aus zwei Rechtecken mit jeweils den gleichen Seitenlängen zusammen. Eine Seite ist bereits mit $\ell= 10,20\,\text{m}$ gegeben.

Die Länge der Seite $c$ kann mit dem Satz des Pythagoras berechnet werden:

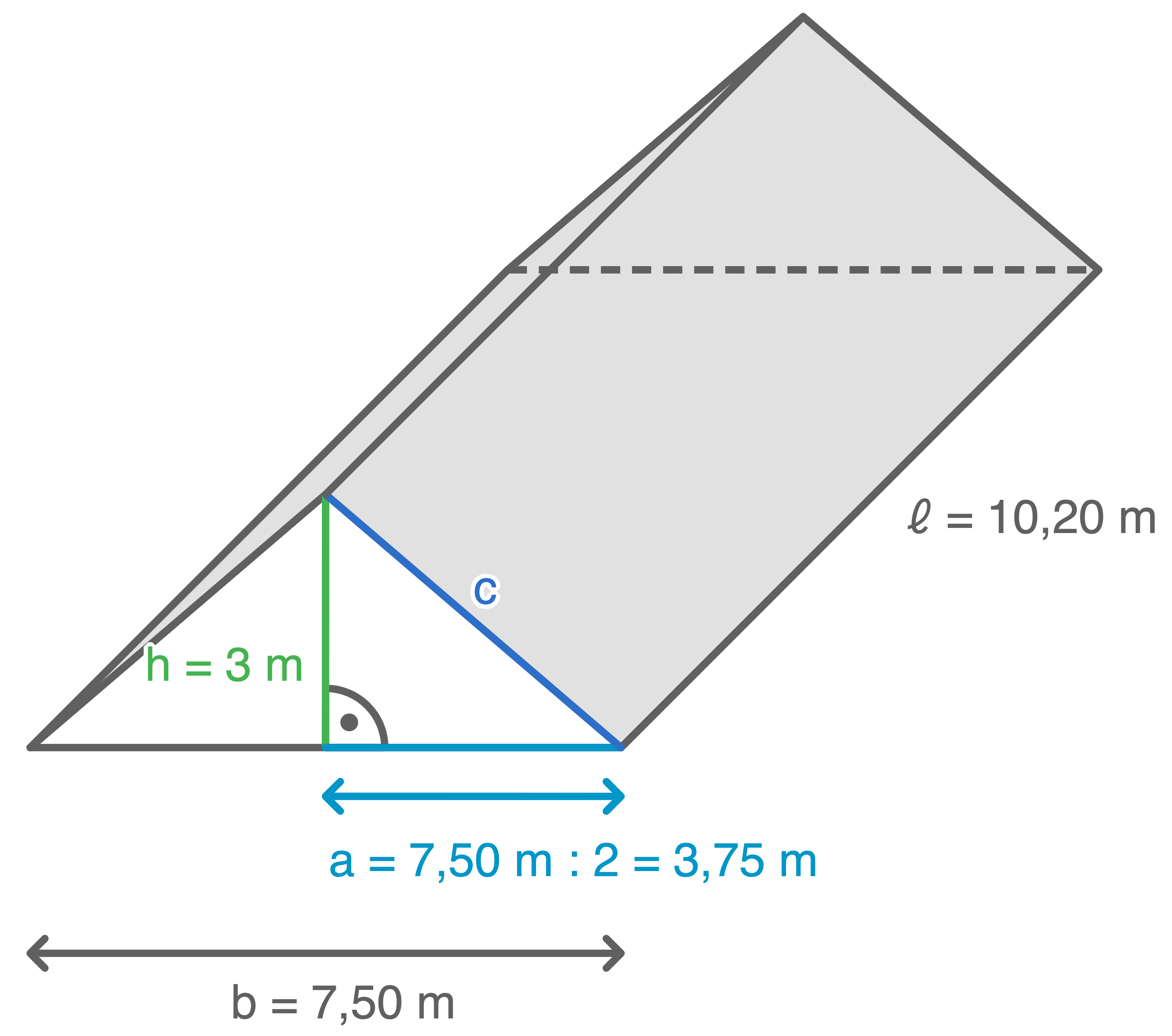
$\begin{array}[t]{rll} c^2&=&h^2+a^2 \\[5pt] c^2&=&(3\,\text{m})^2+(3,75\,\text{m})^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt] c&=&\sqrt{(3\,\text{m})^2+(3,75\,\text{m})^2} \\[5pt] c&\approx&4,8\,\text{m} \\[5pt] \end{array}$

Flächeninhalt eines Rechtecks berechnen

$\begin{array}[t]{rll} A_1&=&c\cdot \ell \\[5pt] A_1&=&4,8\,\text{m}\cdot 10,20\,\text{m} \\[5pt] A_1&=&48,96\,\text{m}^2 \end{array}$

Flächeninhalt der gesamten Dachfläche berechnen

$\begin{array}[t]{rll} A_\text{gesamt}&=&2\cdot A_1 \\[5pt] A_\text{gesamt}&=&2\cdot 48,96\,\text{m}^2 \\[5pt] A_\text{gesamt}&=&97,92\,\text{m}^2 \\[5pt] \end{array}$

Die Dachfläche hat eine Größe von $97,92\,\text{m}^2.$

Lösung 4

Auswahl an Eurobanknoten	Anzahl der Eurobanknoten	Wert
$5 \,€$	$1,66$ Mrd.	$8,30$ Mrd. $\,€$
$10 \,€$	$2\,112$ Mio.	$21,12$ Mrd. $\,€$
$50 \,€$	$7\,615$ Mio.	$358,28$ Mio. $\,€$
$200 \,€$	$202$ Mio.	$40,40$ Mrd. $\,€$

Rechnungen

Anzahl der $5 \,€$ -Eurobanknoten: $8,30$ Mrd. $\,€:5 \,€=1,66$ Mrd.

Wert der $50 \,€$ -Eurobanknoten: $50\,€\cdot 7\,615$ Mio. $=358,28$ Mio. $\,€$

Dreisatz anwenden:

Dreisatz anzeigen

Durchschnittlich sind etwa $379$ gefälschte Geldscheine in Mannheim im Umlauf.

Flächeninhalt eines 50-Euro-Scheines berechnen

$\begin{array}[t]{rll} A_1&=&a\cdot b \\[5pt] A_1&=&140\,\text{mm}\cdot 77\,\text{mm} \\[5pt] A_1&=&10\,780\,\text{mm}^2 \\[5pt] &=&107,8\,\text{cm}^2 \\[5pt] \end{array}$

Flächeninhalt aller 50-Euro-Scheine berechnen

$\begin{array}[t]{rll} A_\text{gesamt}&=& 5,4\,\text{Mrd.}\cdot A_1 \\[5pt] A_\text{gesamt}&=& 5,4\,\text{Mrd.}\cdot 107,8\,\text{cm}^2 \\[5pt] A_\text{gesamt}&=& 582,12\,\text{Mrd.}\,\text{cm}^2 \\[5pt] &=& 582\,120\,000\,000\,\text{cm}^2 \\[5pt] &=& 58,212\,\text{km}^2 \\[5pt] \end{array}$

Weinheim hat eine Fläche von $58,212\,\text{km}^2.$