Wahlaufgaben

Aufgabe 1: Mathematikprüfung

Natalia hat in den Mathematikarbeiten folgende Ergebnisse erzielt:

1. Arbeit	$2,1$
2. Arbeit	$2,9$
3. Arbeit	$2,5$
4. Arbeit	$2,0$
5. Arbeit	$3,0$
6. Arbeit	?

Berechne den Durchschnitt der ersten fünf Arbeiten.
Welche Note müsste Natalia in der $6.$ Arbeit schreiben, damit sie genau auf einen Durchschnitt von $2,4$ kommt?

(2 Pkt.)

Ein DIN-A4-Blatt hat die Maße 210 mm x 297 mm.
Wie viel Prozent davon deckt der abgebildete Kasten mit der Grußbotschaft der Prüfungskommission ab?

(2 Pkt.)

Eine Mathematikprüfung besteht aus $8$ Blättern.
Angenommen $20\,000$ Schülerinnen und Schüler schreiben diese Prüfung.
Würden alle Prüfungsblätter übereinander gestapelt die Höhe des Stuttgarter Bahnhofturms erreichen?
Begründe rechnerisch.

Dicke eines Prüfungsblattes: $\quad \,\,\,\,2 \cdot 10^{-2} \,\text{cm}$
Höhe des Stuttgarter Bahnhofturms: $\quad 56 \,\text{m}$

(2 Pkt.)

Aufgabe 2: Ausflüge in Baden-Württemberg

Tobias sagt: „Im Europapark waren genau viermal mehr Besucher als in der Wilhelma!"
Stimmt das? Begründe rechnerisch.
Wie viele Besucher mehr hatte die Wilhelma als die Insel Mainau?

(2 Pkt.)

2016 wurde der Europapark von $5,6$ Mio. Menschen besucht.
2017 waren es $1,8 \,\%$ mehr. Von den Besuchern 2017 kamen $\dfrac{1}{4}$ aus Frankreich.
Wie viele Besucher kamen 2017 aus Frankreich?

(2 Pkt.)

Die Insel Mainau liegt im Bodensee und sie ist ein beliebtes Urlaubsziel in Baden-Württemberg.
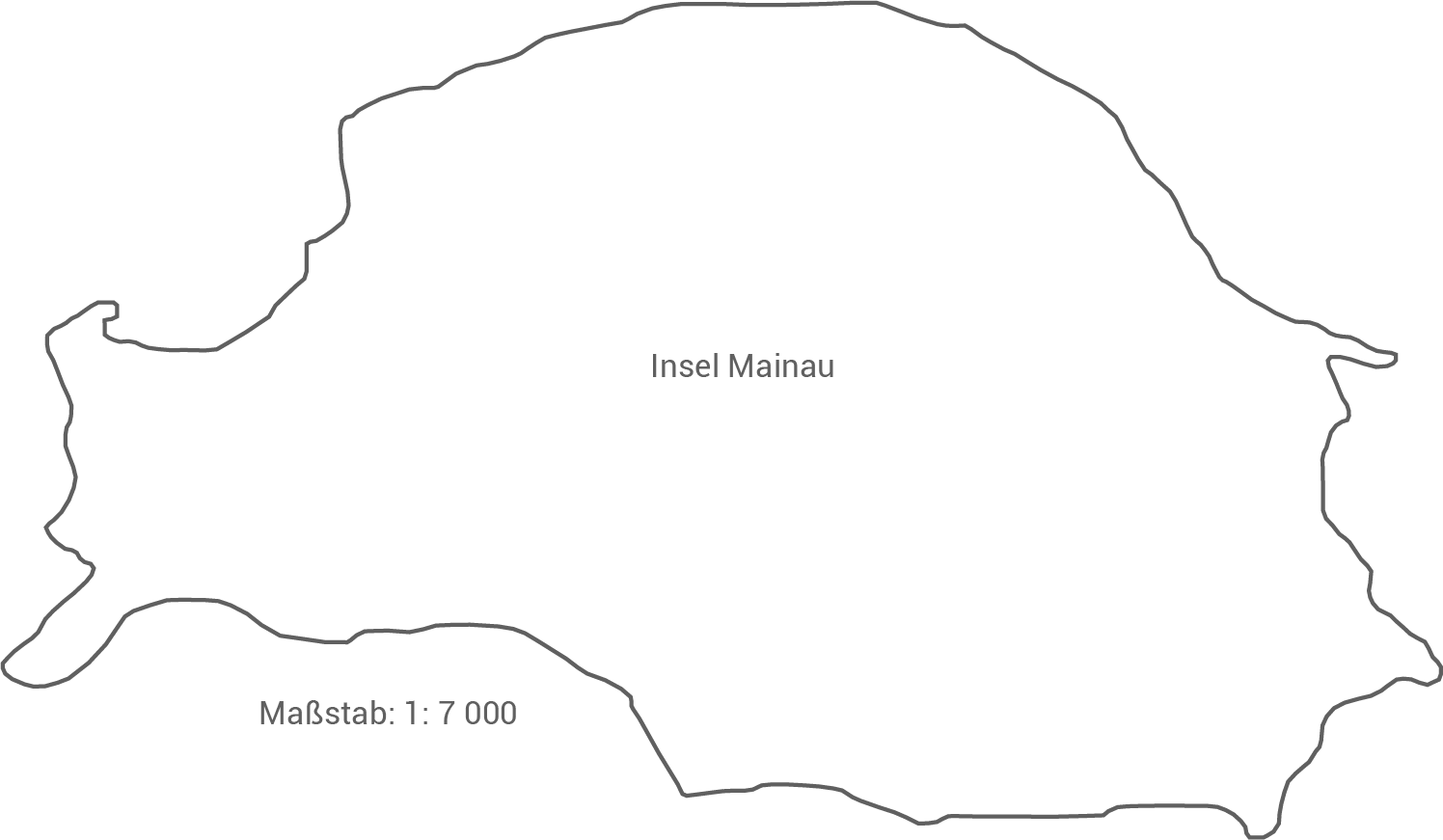
Ermittle den Flächeninhalt der Insel möglichst genau.

2019 HSA BAWÜ Insel Mainau Flächeninhalt

(2 Pkt.)

Aufgabe 3: Plastiktüten

Vom Jahr 2015 zum Jahr 2016 ist die Anzahl der Plastiktüten um $1,9$ Mrd. gesunken.
Zeichne die Säule für das Jahr 2016 in das Diagramm ein.

(2 Pkt.)

Ein quaderförmiger Mülleimer hat folgende Maße:
Breite: $22 \,\text{cm};$ Länge: $30 \,\text{cm};$ Höhe: $30 \,\text{cm}$ .

Ein Warenhaus bietet Mülltüten in folgenden Größen an:

10 Liter

15 Liter

20 Liter

50 Liter

Welche Größe passt am besten für diesen Mülleimer?
Begründe rechnerisch.

(2 Pkt.)

Ines behauptet, wenn man alle Plastiktüten des Jahres 2017 aneinanderlegt, kann man die Fläche des Bodensees bedecken.

Hat sie mit ihrer Behauptung recht?
Begründe rechnerisch.

(2 Pkt.)

Aufgabe 4: Eishockey

Ein Eishockeypuck hat die Form eines Zylinders.

Zeichnung nicht maßstabsgetreu

Berechne das Volumen des abgebildeten Eishockeypucks.

(2 Pkt.)

Eishockeytabelle

Berechnung der Punkte:

Der Sieger eines Spiels erhält 3 Punkte.
Der Sieger nach Verlängerung eines Spiels erhält 2 Punkte.
Der Verlierer nach Verlängerung eines Spiels erhält 1 Punkt.

Berechne die Punkte von zwei Eishockeyteams deiner Wahl.

(2 Pkt.)

Zeichnung nicht maßstabsgetreu

Wie weit liegt der Puck vom Tor entfernt?

(2 Pkt.)

Lösung 1

Durchschnitt der ersten fünf Arbeiten berechnen

$\dfrac{2,1+2,9+2,5+2,0+3,0}{5}=\dfrac{12,5}{5}=2,5$

Welche Note müsste Natalia in der 6. Arbeit schreiben?

Die Unbekannte $x$ steht für die Note der 6. Arbeit:

$\begin{array}[t]{rll} \dfrac{2,1+2,9+2,5+2,0+3,0+x}{6}&=&2,4 \\[5pt] 2,1+2,9+2,5+2,0+3,0+x&=&2,4\cdot 6 \\[5pt] 12,5+x&=&14,4 \\[5pt] x&=&1,9 \end{array}$

Flächeninhalt eines DIN-A-4-Blattes berechnen

$\begin{array}[t]{rll} A_\text{Blatt}&=&a\cdot b \\[5pt] A_\text{Blatt}&=&210\,\text{mm}\cdot 297\,\text{mm} \\[5pt] A_\text{Blatt}&=&62\,370\,\text{mm}^2 \end{array}$

Flächeninhalt des Kastens berechnen

Durch Abmessen erhält man:

$a=74\,\text{mm}$
$b=52\,\text{mm}$

Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

Damit kann der Flächeninhalt eines Rechtecks berechnet werden:
$\begin{array}[t]{rll} A_\text{Kasten}&=&a\cdot b \\[5pt] A_\text{Kasten}&=&74\,\text{mm}\cdot 52\,\text{mm} \\[5pt] A_\text{Kasten}&=&3\,848\,\text{mm}^2 \end{array}$

Verhältnis berechnen

$\dfrac{3\,848}{62\,370}\approx 0,062=6,2\,\%$

Der Kasten deckt etwa $6,2\,\%$ ab.

Dicke einer Mathematikprüfung: $8\cdot 2 \cdot 10^{-2}\,\text{cm}=\dfrac{4}{25}\,\text{cm}=0,16\,\text{cm}$

Dicke aller Mathematikprüfungen: $20\,000\cdot0,16\,\text{cm}=3\,200\,\text{cm}=32\,\text{m}$

Der Stapel Prüfungsblätter erreicht nicht die Höhe des Stuttgarter Bahnhofturms.

Lösung 2

Aussage überprüfen

Die Wilhelma hatte $1,3\,\text{Mio}.$ Besucher.
4-mal mehr als $1,3\,\text{Mio}.$ entspricht: $(1,3+4\cdot 1,3)\,\text{Mio}.=6,5\,\text{Mio.}$

Da der Europapark aber $5,6\,\text{Mio}.$ Besucher hatte, stimmt die Aussage nicht.

Wie viele Besucher mehr hatte die Wilhelma als die Insel Mainau?

$1,30\,\text{Mio}.-1,27\,\text{Mio}.=0,03\,\text{Mio}.=30\,000$

Die Wilhelma hatte $30\,000$ Besucher mehr.

Besucheranzahl im Jahr 2017: $5,6\,\text{Mio.}\cdot 1,018=5,7\,008\,\text{Mio.}=5\,700\,800$

Besucheranzahl aus Frankreich: $\dfrac{1}{4}\cdot 5\,700\,800=1\,425\,200$

Im Jahr 2017 kamen $1\,425\,200$ Besucher aus Frankreich.

Um den Flächeninhalt zu berechnen, wird die Fläche in berechenbare Teilflächen zerlegt.

Eine mögliche Zerlegung:

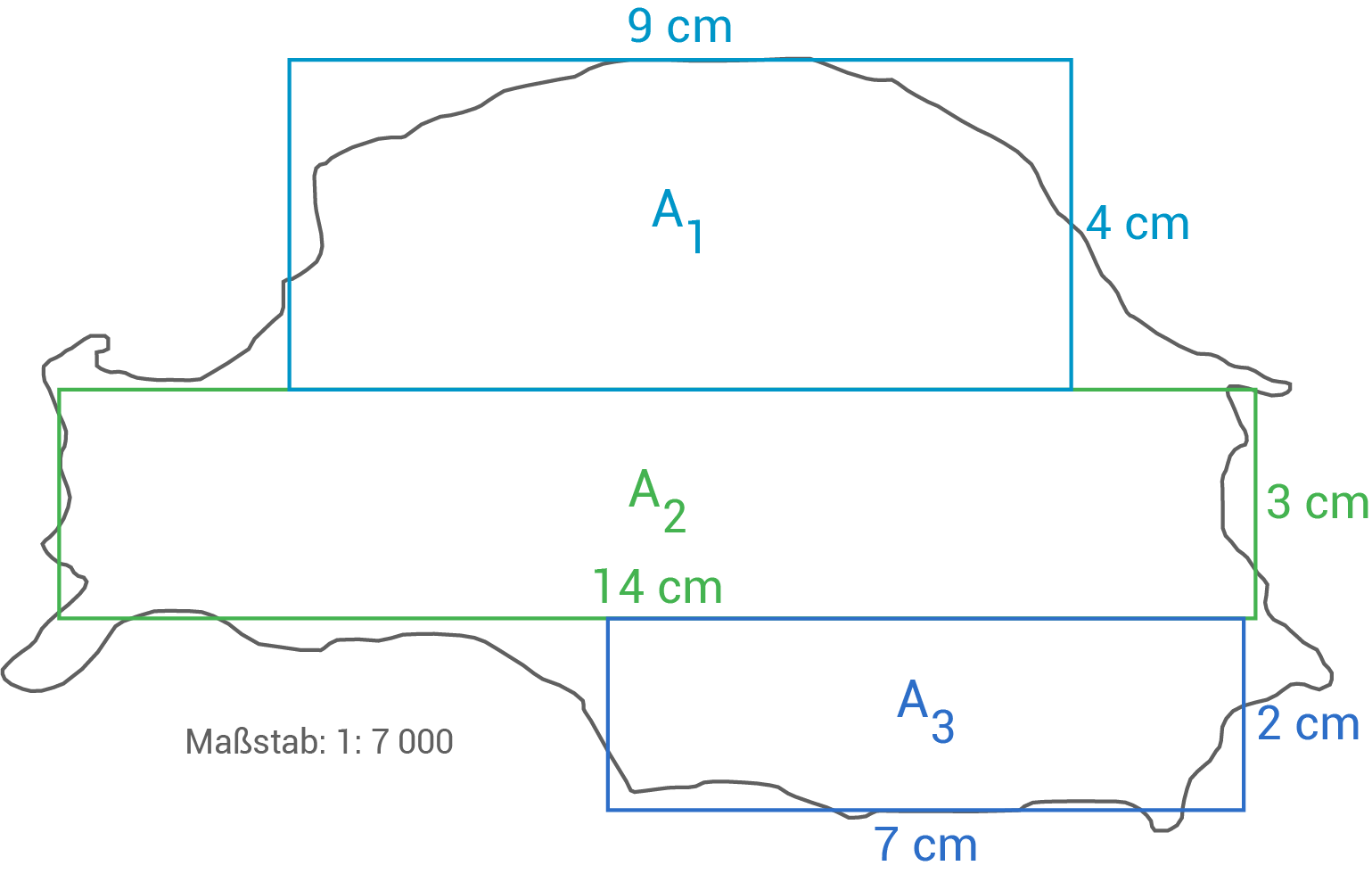hauptschulabschluss mathe 2019 baden-württemberg

Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

Zunächst müssen die wirklichen Längen berechnet werden. Der Maßstab 1:7000 bedeutet:
$1\,\text{cm}\mathrel{\widehat{=}}7\,000\,\text{cm},$ also
$1\,\text{cm}\mathrel{\widehat{=}}70\,\text{m}$

Flächeninhalt von $A_1$ berechnen

$a_1=9\cdot 70\,\text{m}=630\,\text{m}$
$b_1=4\cdot 70\,\text{m}=280\,\text{m}$

$\begin{array}[t]{rll} A_1&=&a_1\cdot b_1 \\[5pt] A_1&=&630\,\text{m}\cdot280\,\text{m} \\[5pt] A_1&=&176\,400\,\text{m}^2 \end{array}$

Flächeninhalt von $A_2$ berechnen

$a_2=3\cdot 70\,\text{m}=210\,\text{m}$
$b_2=14\cdot 70\,\text{m}=980\,\text{m}$

$\begin{array}[t]{rll} A_2&=&a_2\cdot b_2 \\[5pt] A_2&=&210\,\text{m}\cdot 980\,\text{m} \\[5pt] A_2&=&205\,800\,\text{m}^2 \end{array}$

Flächeninhalt von $A_3$ berechnen

$a_3=2\cdot 70\,\text{m}=140\,\text{m}$
$b_3=7\cdot 70\,\text{m}=490\,\text{m}$

$\begin{array}[t]{rll} A_3&=&140\,\text{m}\cdot 490\,\text{m} \\[5pt] A_3&=&68\,600\,\text{m}^2 \end{array}$

Flächeninhalt der Gesamtfläche berechnen

$\begin{array}[t]{rll} A_{\text{gesamt}}&=& A_1+A_2+A_3 \\[5pt] A_{\text{gesamt}}&=& 176\,400\,\text{m}^2+205\,800\,\text{m}^2+68\,600\,\text{m}^2 \\[5pt] A_{\text{gesamt}}&=& 450\,800\,\text{m}^2 \\[5pt] \end{array}$

Der Flächeninhalt der Insel beträgt $450\,800\,\text{m}^2.$

Lösung 3

Durch Abmessen an der senkrechten Achse erkennt man: $5\,\text{mm}$ Säule entsprechen $1\,\text{Mrd.}$ Plastiktüten.

Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

Somit gilt: $1,9\,\text{Mrd.}$ Plastiktüten entsprechen $1,9\cdot 5\,\text{mm}=9,5\,\text{mm}.$

Für 2016 muss also eine Säule gezeichnet werden, die um $9,5\,\text{mm}$ kürzer ist als die für 2015:

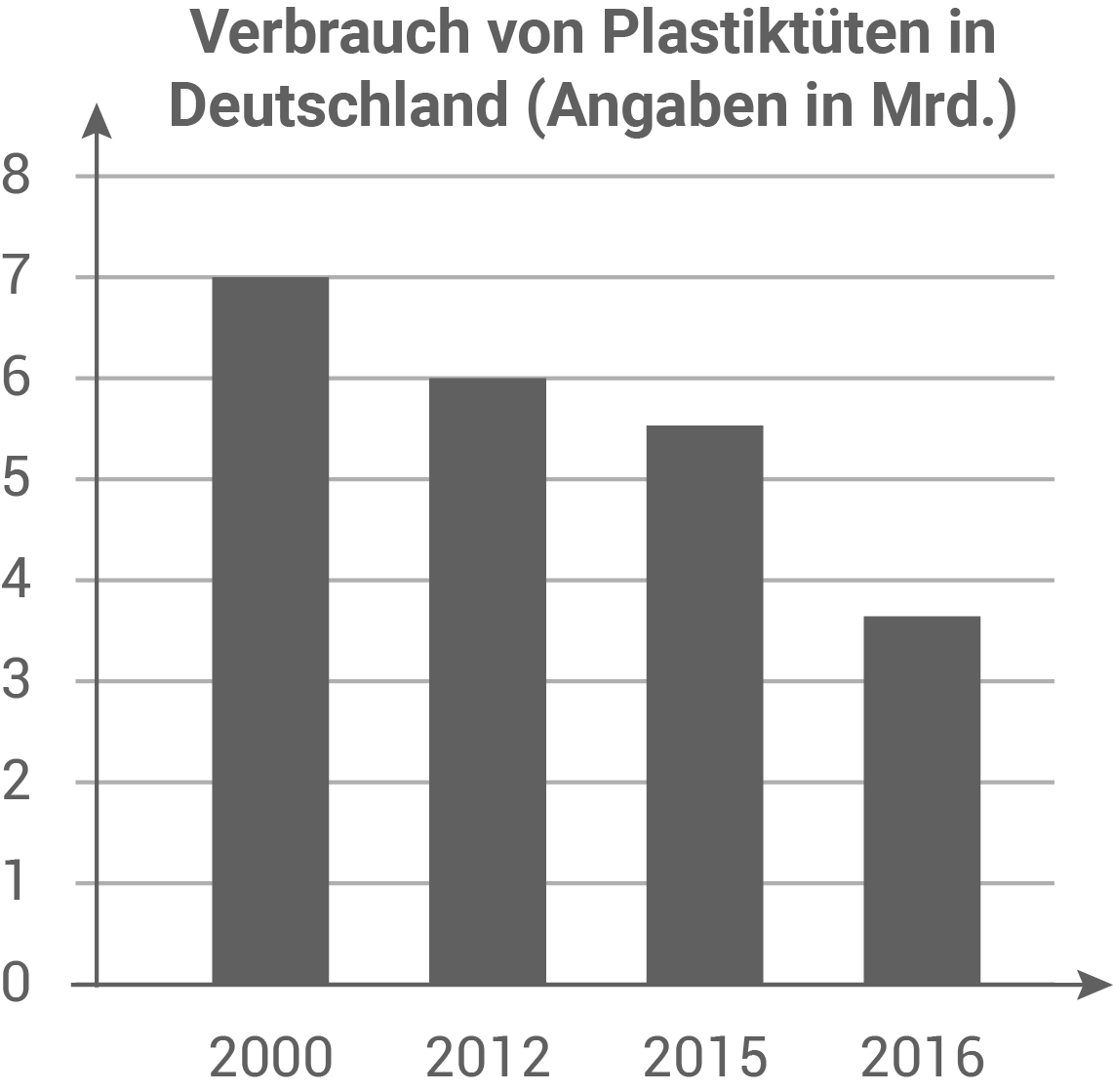
Länge der Säule für 2015: $27,5\,\text{mm}$
Länge der Säule für 2016: $27,5\,\text{mm}-9,5\,\text{mm}=18\,\text{mm}$

Volumen des quaderförmigen Mülleimers berechnen

$\begin{array}[t]{rll} V&=&a\cdot b\cdot c \\[5pt] V&=&22\,\text{cm}\cdot 30 \,\text{cm}\cdot 30 \,\text{cm} \\[5pt] V&=&19\,800\,\text{cm}^3 \\[5pt] \end{array}$

Umrechnung in Liter

$19\,800\,\text{cm}^3=19,8\,\text{dm}^3=19,8\,\text{l}$

Die Mülltüte mit $20\,\text{l}$ passt am besten.

Flächeninhalt einer Plastiktüte berechnen

$\begin{array}[t]{rll} A_{\text{Tüte}}&=& 50\,\text{cm}\cdot 30\,\text{cm} \\[5pt] A_{\text{Tüte}}&=& 1\,500\,\text{cm}^2\\[5pt] &=& 15\,\text{dm}^2\\[5pt] &=& 0,15\,\text{m}^2\\[5pt] \end{array}$

Flächeninhalt aller Plastiktüten berechnen

$\begin{array}[t]{rll} A_{\text{gesamt}}&=&2,4\,\text{Mrd.}\cdot 0,15\,\text{m}^2 \\[5pt] A_{\text{gesamt}}&=&0,36\,\text{Mrd.}\,\text{m}^2 \\[5pt] &=&0,36\cdot 1\,000\,000\,000\,\text{m}^2 \\[5pt] &=&360\,000\,000\,\text{m}^2 \\[5pt] &=&3\,600\,000\,\text{a} \\[5pt] &=&36\,000\,\text{ha} \\[5pt] &=&360\,\text{km}^2 \\[5pt] \end{array}$

Die Behauptung ist falsch, da der Bodensee eine Fläche von $536\,\text{km}^2$ hat und somit größer ist.

Lösung 4

Zur Berechnung des Volumens wird der Radius des Pucks benötigt:

$\begin{array}[t]{rll} r&=&d:2 \\[5pt] r&=&7,62\,\text{cm}:2 \\[5pt] r&=&3,81\,\text{cm} \end{array}$

Damit lässt sich nun das Volumen berechnen:

$\begin{array}[t]{rll} V&=&\pi\cdot r^2\cdot h \\[5pt] V&=&\pi\cdot (3,81\,\text{cm})^2\cdot 2,54\,\text{cm} \\[5pt] V&\approx&115,83\,\text{cm}^3 \\[5pt] \end{array}$

Es reicht, die Punkte von zwei Eishockeyteams anzugeben:

München

Punkte: $107$
Rechnung: $30\cdot 3+6\cdot 2+5\cdot 1=107$

Berlin

Punkte: $101$
Rechnung: $29\cdot 3+4\cdot 2+6\cdot 1=101$

Nürnberg

Punkte: $100$
Rechnung: $25\cdot 3+10\cdot 2+5\cdot 1=101$

Ingolstadt

Punkte: $79$
Rechnung: $20\cdot 3+6\cdot 2+7\cdot 1=79$

Mannheim

Punkte: $78$
Rechnung: $21\cdot 3+6\cdot 2+3\cdot 1=78$

Die Entfernung kann mihilfe des Satz des Pythagoras berechnet werden:

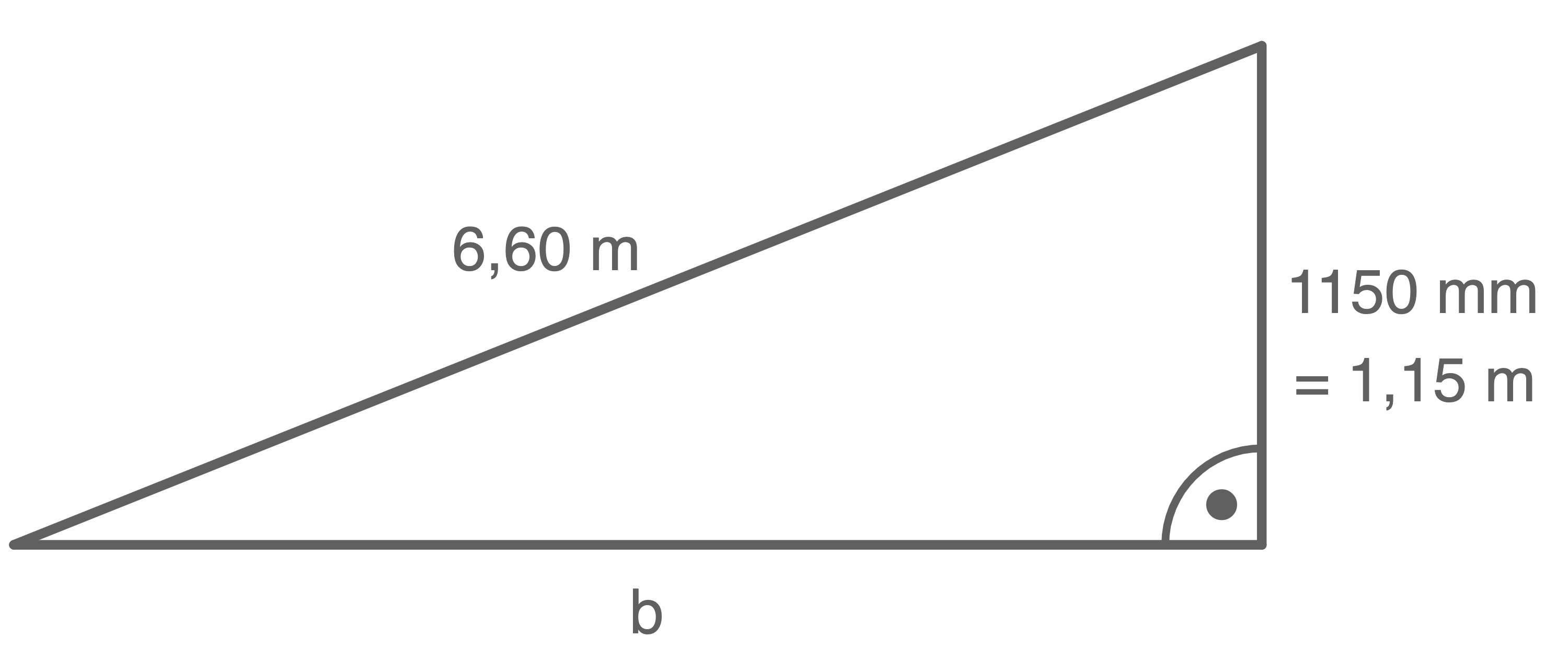Rechnung zur Höhe: $1\,220\,\text{mm}-70\,\text{mm}=1\,150\,\text{mm}=1,15\,\text{m}$

Berechnung der Entfernung:

$\begin{array}[t]{rll} a^2+b^2&=&c^2 &\quad \scriptsize \mid\;-a^2 \\[5pt] b^2&=&c^2-a^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt] b&=&\sqrt{c^2-a^2} \\[5pt] b&=&\sqrt{(6,60\,\text{m})^2-(1,15\,\text{m})^2} \\[5pt] b&\approx&6,50\,\text{m} \end{array}$

Der Puck liegt etwa $6,50\,\text{m}$ vom Tor entfernt.